第5章 自变量的选择与逐步回归
- 格式:ppt
- 大小:1.50 MB
- 文档页数:55

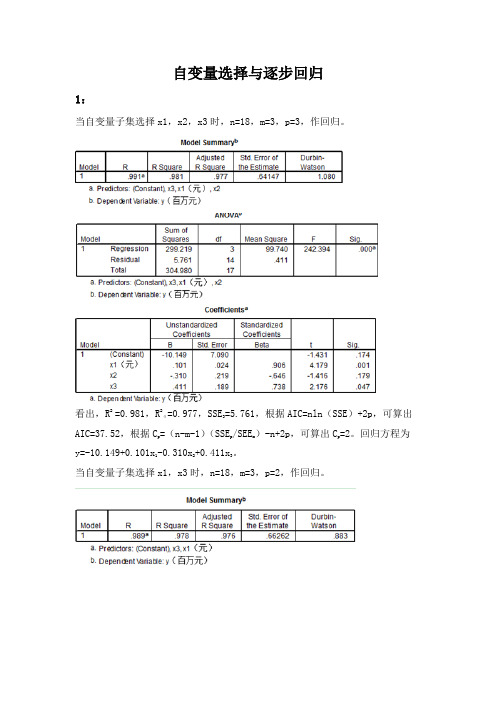
自变量选择与逐步回归1:当自变量子集选择x1,x2,x3时,n=18,m=3,p=3,作回归。
看出,R2 =0.981,R2α=0.977,SSE3=5.761,根据AIC=nln(SSE)+2p,可算出AIC=37.52,根据Cp =(n-m-1)(SSEp/SEEm)-n+2p,可算出Cp=2。
回归方程为y=-10.149+0.101x1-0.310x2+0.411x3。
当自变量子集选择x1,x3时,n=18,m=3,p=2,作回归。
得出:R2 =0.978,R2α=0.976,SSE2=6.586,根据AIC=nln(SSE)+2p,可算出AIC=37.93,根据Cp =(n-m-1)(SSEp/SEEm)-n+2p,可算出Cp=2.005。
回归方程为y=-14.049+0.076x1+0.172x3。
当自变量子集选择x1时,n=18,m=3,p=1,作回归。
得出:R2 =0.973,R2α=0.971, SSE1=8.285,根据AIC=nln(SSE)+2p,可算出AIC=40.06,根据Cp =(n-m-1)(SSEp/SEEm)-n+2p,可算出Cp=4.134。
回归方程为y=-0.821+0.110x。
12:前进法:在Model下拉框中选择前进法Forward,点击Options看到默认的显著性水平为0.05,运行得:从输出结果看到,前进法依次引入了x1,x2,x3,x6,x7,最优模型为y=-2393.975+1.490x1+2.718x2+2.209x3+0.078x6+0.037x7。
复决定系数R2 =0.992,调整的复决定系数R2α=0.991,全模型的复决定系数R2 =0.994,调整的复决定系数R2α=0.991。
后退法:在Model下拉框中选择前进法Backward,点击Options看到默认的显著性水平为0.10,运行得:其中模型1是全模型,从模型2到模型4依次剔除变量x4,x8,x9,最优回归子集模型4的回归方程为:y=-2089.883+1.412x1+2.395x2+2.021x3+0.077x6+0.036x7+0.859x5复决定系数R2 =0.993调整的复决定系数R2α=0.992全模型的复决定系数R2 =0.994,调整的复决定系数R2α=0.991。


《应用回归分析》自变量选择与逐步回归实验报告二、实验步骤:(只需关键步骤)步骤一:对六个回归自变量x1,x2……x6分别同因变量Y建立一元回归模型步骤二:分别计算这六个一元回归的六个回归系数的F检验值。
步骤三:将因变量y 分别与(x1, x2),(x1, x3), …, (x1, x m)建立m-1个二元线性回归方程, 对这m-1个回归方程中x2, x3, …, x m的回归系数进行F 检验,计算 F 值步骤四:重复步骤二。
三、实验结果分析:(提供关键结果截图和分析)1.建立全模型回归方程;由上图结果可知该问题的全模型方程为:Y=1347.986-0.641x1-0.317x2-0.413x3-0.002x4+0.671x5-0.008x62.用前进法选择自变量;从右图上可以看出:依次引入了变量x5、x1、x2最优回归模型为:Y^=874.583-0.611x1-0.353x2+0.637x5最优模型的复决定系数 :R^2=0.996调整后的复决定系数:R^2=0.9953.用后退法选择自变量;从上图上可以看出:依次剔除变量x4、x3、x6最优回归模型为:y^=874.583-0.611x1-0.353x2+0.637x5最优模型的复决定系数 R^2=0.996调整后的复决定系数R^2=0.995最优模型的复决定系数R^2=0.996调整后的复决定系数R^2=0.9954.用逐步回归法选择自变量;从上图上可以看出:依次引入了变量x5、x1、x2最优回归模型为:y^=874.583-0.611x1-0.353x2+0.637x5最优模型的复决定系数 R^2=0.996调整后的复决定系数R^2=0.9955.根据以上结果分三种方法的差异。
前进法和后退法以及逐步回归法的计算结果完全一致,但是在其计算上又有很大的差异,前进法就是当自变量一旦被选入,就永远保留在模型中。
后退法就是反向法,而逐步回归就比后退法更明确,逐步后退回归的方法。

自变量选择与逐回归————————————————————————————————作者:————————————————————————————————日期:自变量选择与逐步回归一、全模型和选模型设研究某一实际问题,涉及对因变量有影响的因素共有m 个,由因变量y 和m 个自变量构成的回归模型εββββ+++++=m m x x x y Λ22110称为全模型。
如果从可供选择的m 个变量中选出p 个,由选出的p 个自变量组成的回归模型p pp pp p p p x x x y εββββ+++++=Λ22110称为选模型。
二、自变量选择对预测的影响自变量选择对预测的影响可以分为两种情况考虑,第一种情况是全模型正确而误用了选模型;第二种情况是选模型正确而无用了全模型。
以下是这两种情况对回归的影响。
1、全模型正确而误用选模型的情况性质1,在j x 与m p x x ,,1Λ+的相关系数不全为0时,选模型回归系数的最小二乘估计是全模型相应参数的有偏估计,即jjp jp E βββ≠=)ˆ((p j ,,2,1Λ=) 性质2,选模型的预测是有偏的。
性质3,选模型的参数估计有较小的方差。
性质4,选模型的预测残差有较小的方差。
性质5,选模型的均方误差比全模型预测的方差更小。
性质1和性质2表明,当全模型正确时,而舍去了m-p 个自变量,用剩下的p 个自变量去建立选模型,参数估计值是全模型相应参数的有偏估计,用其做预测,预测值也是有偏的。
这是误用选模型产生的弊端。
性质3和性质4表明,用选模型去作预测,残差的方差比用全模型去作预测的方差小,尽管用选模型所作的预测是有偏的,但得到的预测残差的方差下降了,这说明尽管全模型正确,误用选模型是有弊也有利的。
性质5说明,即使全模型正确,但如果其中有一些自变量对因变量影响很小或回归系数方差过大,丢掉这些变量之后,用选模型去预测,可以提高预测的精度。
由此可见,如果模型中包含了一些不必要的自变量,模型的预测精度就会下降。

第5章自变量选择与逐步回归思考与练习参考答案自变量选择对回归参数的估计有何影响答:回归自变量的选择是建立回归模型得一个极为重要的问题。
如果模型中丢掉了重要的自变量, 出现模型的设定偏误,这样模型容易出现异方差或自相关性,影响回归的效果;如果模型中增加了不必要的自变量, 或者数据质量很差的自变量, 不仅使得建模计算量增大, 自变量之间信息有重叠,而且得到的模型稳定性较差,影响回归模型的应用。
自变量选择对回归预测有何影响答:当全模型(m元)正确采用选模型(p元)时,我们舍弃了m-p个自变量,回归系数的最小二乘估计是全模型相应参数的有偏估计,使得用选模型的预测是有偏的,但由于选模型的参数估计、预测残差和预测均方误差具有较小的方差,所以全模型正确而误用选模型有利有弊。
当选模型(p元)正确采用全模型(m 元)时,全模型回归系数的最小二乘估计是相应参数的有偏估计,使得用模型的预测是有偏的,并且全模型的参数估计、预测残差和预测均方误差的方差都比选模型的大,所以回归自变量的选择应少而精。
如果所建模型主要用于预测,应该用哪个准则来衡量回归方程的优劣C统计量达到最小的准则来衡量回答:如果所建模型主要用于预测,则应使用p归方程的优劣。
试述前进法的思想方法。
答:前进法的基本思想方法是:首先因变量Y对全部的自变量x1,x2,...,xm建立m 个一元线性回归方程, 并计算F检验值,选择偏回归平方和显着的变量(F值最大且大于临界值)进入回归方程。
每一步只引入一个变量,同时建立m-1个二元线性回归方程,计算它们的F检验值,选择偏回归平方和显着的两变量变量(F 值最大且大于临界值)进入回归方程。
在确定引入的两个自变量以后,再引入一个变量,建立m-2个三元线性回归方程,计算它们的F检验值,选择偏回归平方和显着的三个变量(F值最大)进入回归方程。
不断重复这一过程,直到无法再引入新的自变量时,即所有未被引入的自变量的F检验值均小于F检验临界值Fα(1,n-p-1),回归过程结束。
自变量选择与逐步回归一、全模型和选模型设研究某一实际问题,涉及对因变量有影响的因素共有m 个,由因变量y 和m 个自变量构成的回归模型εββββ+++++=m m x x x y 22110称为全模型。
如果从可供选择的m 个变量中选出p 个,由选出的p 个自变量组成的回归模型p pp pp p p p x x x y εββββ+++++= 22110称为选模型。
二、自变量选择对预测的影响自变量选择对预测的影响可以分为两种情况考虑,第一种情况是全模型正确而误用了选模型;第二种情况是选模型正确而无用了全模型。
以下是这两种情况对回归的影响。
1、全模型正确而误用选模型的情况性质1,在j x 与m p x x ,,1 +的相关系数不全为0时,选模型回归系数的最小二乘估计是全模型相应参数的有偏估计,即jjp jp E βββ≠=)ˆ((p j ,,2,1 =) 性质2,选模型的预测是有偏的。
性质3,选模型的参数估计有较小的方差。
性质4,选模型的预测残差有较小的方差。
性质5,选模型的均方误差比全模型预测的方差更小。
性质1和性质2表明,当全模型正确时,而舍去了m-p 个自变量,用剩下的p 个自变量去建立选模型,参数估计值是全模型相应参数的有偏估计,用其做预测,预测值也是有偏的。
这是误用选模型产生的弊端。
性质3和性质4表明,用选模型去作预测,残差的方差比用全模型去作预测的方差小,尽管用选模型所作的预测是有偏的,但得到的预测残差的方差下降了,这说明尽管全模型正确,误用选模型是有弊也有利的。
性质5说明,即使全模型正确,但如果其中有一些自变量对因变量影响很小或回归系数方差过大,丢掉这些变量之后,用选模型去预测,可以提高预测的精度。
由此可见,如果模型中包含了一些不必要的自变量,模型的预测精度就会下降。
2、选模型正确而误用全模型的情况全模型的预测值是有偏估计;选模型的预测方差小于全模型的预测方差;全模型的预测误差将更大。
自变量选择与逐步回归一、全模型和选模型设研究某一实际问题,涉及对因变量有影响的因素共有m 个,由因变量y 和m 个自变量构成的回归模型εββββ+++++=m m x x x y 22110称为全模型。
如果从可供选择的m 个变量中选出p 个,由选出的p 个自变量组成的回归模型p pp pp p p p x x x y εββββ+++++= 22110称为选模型。
二、自变量选择对预测的影响自变量选择对预测的影响可以分为两种情况考虑,第一种情况是全模型正确而误用了选模型;第二种情况是选模型正确而无用了全模型。
以下是这两种情况对回归的影响。
1、全模型正确而误用选模型的情况性质1,在j x 与m p x x ,,1 +的相关系数不全为0时,选模型回归系数的最小二乘估计是全模型相应参数的有偏估计,即jjp jp E βββ≠=)ˆ((p j ,,2,1 =) 性质2,选模型的预测是有偏的。
性质3,选模型的参数估计有较小的方差。
性质4,选模型的预测残差有较小的方差。
性质5,选模型的均方误差比全模型预测的方差更小。
性质1和性质2表明,当全模型正确时,而舍去了m-p 个自变量,用剩下的p 个自变量去建立选模型,参数估计值是全模型相应参数的有偏估计,用其做预测,预测值也是有偏的。
这是误用选模型产生的弊端。
性质3和性质4表明,用选模型去作预测,残差的方差比用全模型去作预测的方差小,尽管用选模型所作的预测是有偏的,但得到的预测残差的方差下降了,这说明尽管全模型正确,误用选模型是有弊也有利的。
性质5说明,即使全模型正确,但如果其中有一些自变量对因变量影响很小或回归系数方差过大,丢掉这些变量之后,用选模型去预测,可以提高预测的精度。
由此可见,如果模型中包含了一些不必要的自变量,模型的预测精度就会下降。
2、选模型正确而误用全模型的情况全模型的预测值是有偏估计;选模型的预测方差小于全模型的预测方差;全模型的预测误差将更大。