苏教版高中数学选修(1-2)-1.2教学建议:独立性检验和回归直线
- 格式:doc
- 大小:26.50 KB
- 文档页数:2



独立性检验的基本思想及其初步应用一、授课内容的数学本质在《数学3(必修)》概率统计内容的基础上,通过典型案例介绍独立性检验的基本思想、方法及其初步应用,使学生认识统计方法在决策中的作用。
章引言首先提出了现实中经常遇到的问题,比如肺癌是严重威胁人类生命的一种疾病,吸烟与患肺癌有关系吗?等等。
现实中类似的问题大量存在,如何得出准确的推断,这就需要科学的方法,独立性检验就是其中一种常用的统计方法。
教科书通过探究“吸烟是否与患肺癌有关系”引出了独立性检验的问题,并借助样本数据的列联表、柱形图和条形图展示在吸烟人中患肺癌的比例比不吸烟人中患肺癌的比例要高,使学生直观感觉到吸烟和患肺癌可能有关系。
“吸烟与患肺癌有关”这一直觉来自于观测数据,即样本。
问题是这种来自于样本的印象能够在多大程度上代表总体?来自于样本的结论“吸烟与患肺癌有关”能够推广到总体吗?为了回答这个问题,就必须借助于统计理论来分析。
在统计学中,独立性检验就是检验两个分类变量是否有关系的一种统计方法。
二、教学目标分析【知识与技能】1、了解独立性检验的基本思想、方法及初步应用。
列联表)、柱形图、条形图直观分析两个分类变量是否有关。
2、会从列联表(只要求22K公式判断两个分类变量在某种可信程度上的相关性。
3、会用2【过程与方法】运用数形结合的方法,借助对典型案例的探究,来了解独立性检验的基本思想,总结独立性检验的基本步骤。
【情感、态度与价值观】1、通过本节课的学习,让学生感受数学与现实生活的联系,体会独立性检验的基本思想在解决日常生活问题中的作用。
2、培养学生运用所学知识,依据独立性检验的思想作出合理推断的实事求是的好习惯。
三、教学问题诊断在独立性检验中,教科书通过典型案例“吸烟是否与患肺癌有关系”的研究,介绍了独立性检验的基本思想、方法和初步应用。
独立性检验的步骤是固定的,仿照教科书的例题,学生不难完成习题,但独立性检验的思想对学生来说是比较难理解的,教学中如何结合例子介绍独立性检验的思想,才能使得学生很好的理解是一个教学难点。

高中选修1-2回归分析和独立性检验知识总结与联系-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN1122211()()()n n i i i i i i n n i i i i x x y y x y nx y b x x x nx a y bx ====⎧---⎪⎪==⎪⎨--⎪⎪=-⎪⎩∑∑∑∑选修1-2第一部分 变量间的相关关系与统计案例【基础知识】一、回归分析1.两个变量的线性相关:判断是否线性相关 ①用散点图(1)正相关:在散点图中,点散布在从左下角到右上角的区域.对于两个变量的这种相关关系,我们将它称为正相关.(2)负相关:在散点图中,点散布在从左上角到右下角的区域,两个变量的这种相关关系称为负相关.(3)线性相关关系、回归直线:如果散点图中点的分布从整体上看大致在一条直线附近,就称这两个变量之间具有线性相关关系,这条直线叫做回归直线. ②用相关系数r(3)除用散点图外,还可用样本相关系数r 来衡量两个变量x ,y 相关关系的强弱,ni ix y nx yr -•=∑当r >0,表明两个变量正相关,当r <0,表明两个变量负相关,r 的绝对值越接近于1,表明两个变量的线性相关性越强;r 的绝对值越接近于0,表明两个变量之间几乎不存在线性相关关系,通常|r |0.75>时,认为这两个变量具有很强的线性相关关系. 2.回归方程:两个变量具有线性相关关系,数据收集如下:可用最小二乘法得到回归方程ˆy bx a =+,其中3.回归分析的基本思想及其初步应用(1)回归分析是对具有相关关系的两个变量进行统计分析的方法,其常用的 研究方法步骤是画出散点图,求出回归直线方程,并利用回归直线方程进行预报.(2)对n 个样本数据(x 1,y 1)、(x 2,y 2)、…、(xn ,yn ),(,)x y 称为样本点的中心.样本点中心一定落在回归直线上。
4、回归效果的刻画:用相关指数2R来刻画回归的效果,公式是2 2121()1()ni iiniiy yRy y==-=--∑∑2R的值越大,说明残差平方和越小,也就是说模型拟合效果好二.独立性检验的基本思想及其初步应用题型一相关关系的判断【例1】对四组数据进行统计,获得以下散点图,关于其相关系数比较,正确的是()A.r2<r4<0<r3<r1B. r4<r2<0<r 1<r3C. r4<r2<0<r3<r1D. r2<r4<0<r1<r3【变式1】 根据两个变量x ,y 之间的观测数据画成散点图如图所示,这两个变量是否具有线性相关关系________(填“是”与“否”).题型二 线性回归方程【例2】在2013年元旦期间,某市物价部门对本市五个商场销售的某商品一天的销售量及其价格进行调查,五个商场的售价x 元和销售量y 件之间的一价格x 9 9.5 10 10.5 11销售量y11 10 8 6 5 y 关于商品的价格x 的线性回归方程为________.(参考公式:b ^= ,a ^=y -b ^x )【变式3】为了解儿子身高与其父亲身高的关系,随机抽取5对父子的身高数据如下:父亲身高x /cm 174 176 176 176 178儿子身高y /cm175 175 176 177 177则y 对x 的线性回归方程为( ). A .y =x -1 B .y =x +1C .y =88+12x D .y =176题型三 独立性检验【例4】通过随机询问110名性别不同的行人,对过马路是愿意走斑马线由K 2=n (ad -dc )(a +b )(c +d)(a +c )(b +d ),算得K 2=110×(40×30-20×20)260×50×60×50≈7.8.附表:A. 有99%以上的把握认为“选择过马路的方式与性别有关”B. 有99%以上的把握认为“选择过马路的方式与性别无关”C. 在犯错误概率不超过0.1%的前提下,认为“选择过马路的方式与性别有关”D. 在犯错误概率不超过0.1%的前提下,认为“选择过马路的方式与性别无关【变式2】 某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出了500件,(2)由以上统计数据填下面2×2列联表,并问是否有99%的把握认为“两个分附 K 2巩固提高1.下列说法:①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;②设有一个回归方程y ^=3-5x ,变量x 增加一个单位时,y 平均增加5个单位;③线性回归方程y ^=b ^x +a ^必过(x ,y );④在一个2×2列联表中,由计算得K 2=13.079,则有99%的把握确认这两个变量间有关系;其中错误的个数是( )A. 0B. 1C. 2D. 32.已知回归直线斜率的估计值为1.23,样本点的中心为点(4,5),则回归直线的方程为( ) A. y ^=1.23x +4 B. y ^=1.23x +5 C. y ^=1.23x +0.08 D. y ^=0.08x +1.23 3.从所得的散点图分析可知:y 与x 线性相关,且y =0.95x +a ,则a =( ) A. 1.30 B. 1.45 C. 1.65 D. 1.804.根据上表可得回归直线方程:y =0.56x +a ,据此模型预报身高为172 cm 的高三男生的体重为( )A. 70.09 kgB. 70.12 kgC. 70.55 kgD. 71.05 kg5.调查了某地若干户家庭的年收入x (单位:万元)和年饮食支出y (单位:万元),调查显示年收入x 与年饮食支出y 具有线性相关关系,并由调查数据得到y 对x的回归直线方程:y ^=0.254x +0.321.由回归方程可知,家庭年收入每增加1万元,年饮食支出平均增加________万元.6.利用独立性检验对两个分类变量是否有关系进行研究时,若在犯错误的概率不超过0.005的前提下认为事件A 和B 有关系,则具体计算出的数据应该是( )A .k≥6.635B .k <6.635C .k≥7.879D .k <7.8797.某高校“统计初步”课程的教师随机调查了选该课的一些学生的情况,具体数据如下表:非统计专业统计专业男13 10女7 20为了判断主修统计专业是否与性别有关系,根据表中数据得到,k=50(13×20-10×7)220×30×23×27≈4.844,因为k>3.841,所以确定主修统计专业与性别有关系,那么这种判断出错的可能性为________.与销售额(单位:百万元)之间有如下对应数据:(1)画出散点图;(2)求线性回归方程;(3)试预测广告费支出为百万元时,销售额多大?9.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程;(3)已知该厂技改前吨甲产品的生产能耗为吨标准煤,试根据(2)求出的线性回归方程,预测生产吨甲产品的生产能耗比技改前降低多少吨标准煤(参考数值:)9.某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:喜欢甜品不喜欢甜品合计南方学生60 20 80北方学生10 10 20合计70 30 100(1)甜品的饮食习惯方面有差异”;(2)已知在被调查的北方学生中有5名数学系学生,其中2名习惯甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.10、我市某校某数学老师这学期分别用两种不同的教学方式试验高一甲、乙两个班(人数均为人,入学数学平均分和优秀率都相同,勤奋程度和自觉性都一样)。

1.2回归分析BCA案主备人:史玉亮审核人:吴秉政使用时间:2012.2.6 学习目标:1.通过对典型案例的探究,进一步了解回归分析的基本思想、方法及初步应用。
2.结合具体的实际问题,了解非线性回归问题的解决思路。
3.通过回归分析的学习,提高对现代计算技术与统计方法的应用意识。
B案一、基础整合1.召与回归系数b?的计算方法b?= _______________________ ,a?= ________________________ 。
2.样本相关系数(1)对于变量x与y随机抽取到的n对数据(x1,y1),(x2,y2),……,(x n,y n),检验统计量是样本相关系数r= ______________________________________________(2)_____________________________________________________________ r具有以下性质:r w 1,并且r越接近1,线性相关程度___________________________________ ;r越接近0,线性相关程度_______________________ 。
(3)检验的步骤如下:①作统计假设:x与y不具有_____________________ 关系。
②根据 __________ 与______________ 在附表中查出r的一个临界值r0.05。
③根据 ____________________ 计算公式算出r的值。
④作统计推断。
如果r| > “a,表明有____________ 的把握认为x与y之间具有线性相关关系;如果|r w r o.05,我们没有理由拒绝__________ 。
这时寻找回归直线方程是毫无意义的。
二、预习检测1.下列两变量具有相关关系的是( )A.正方体的体积与棱长B.匀速行驶的车辆的行驶距离与时间C.人的身高与体重D.人的身高与视力2.下列两变量是线性相关的是( )A.如果变量X与Y之间存在着线性相关关系,则我们根据试验数据得到的点(X i, yj(i =1,2,3,...,n)将散布在某一条直线附近B.如果两个变量X与Y之间不存在线性关系,那么根据试验数据不能写出一个线性方程C.设x、y是具有线性相关关系的两个变量,且回归直线方程是(•召,则b?叫回归系数D.为使求出的回归直线方程有意义,可用统计假设检验的方法判断变量X与Y之间是否存在线性相关关系4.在一次试验中,测得(x, y)的四组值分别是A(1,2), B(2,3),C(3,4), D(4,5),则y 与x之间的回归直线方程为()A. y?=x1B. ?=x 2C. ? = 2x1D. y? = x-1C案合作探究1.回归直线方程的适用范围是什么?2.建立回归直线方程的一般步骤是什么?3.由回归直线方程得到的变量的值是真实值吗?例某工厂月份某种产品的产量与成本的统计数据见下表。

第一课时 1.1独立性检验的基本思想及其初步应用(一)教学要求:通过探究“吸烟是否与患肺癌有关系”引出独立性检验的问题,并借助样本数据的列联表、柱形图和条形图展示在吸烟者中患肺癌的比例比不吸烟者中患肺癌的比例高,让学生亲身体验独立性检验的实施步骤与必要性.教学重点:理解独立性检验的基本思想及实施步骤.教学难点:了解独立性检验的基本思想、了解随机变量2K的含义.教学过程:一、复习准备:回归分析的方法、步骤,刻画模型拟合效果的方法(相关指数、残差分析)、步骤.二、讲授新课:1. 教学与列联表相关的概念:①分类变量:变量的不同“值”表示个体所属的不同类别的变量称为分类变量. 分类变量的取值一定是离散的,而且不同的取值仅表示个体所属的类别,如性别变量,只取男、女两个值,商品的等级变量只取一级、二级、三级,等等. 分类变量的取值有时可用数字来表示,但这时的数字除了分类以外没有其他的含义. 如用“0”表示“男”,用“1”表示“女”.②列联表:分类变量的汇总统计表(频数表). 一般我们只研究每个分类变量只取两个值,这样的列联表称为22⨯. 如吸烟与患肺癌的列联表:2. 教学三维柱形图和二维条形图的概念:由列联表可以粗略估计出吸烟者和不吸烟者患肺癌的可能性存在差异.(教师在课堂上用EXCEL软件演示三维柱形图和二维条形图,引导学生观察这两类图形的特征,并分析由图形得出的结论)3. 独立性检验的基本思想:①独立性检验的必要性(为什么中能只凭列联表的数据和图形下结论?):列联表中的数据是样本数据,它只是总体的代表,具有随机性,故需要用列联表检验的方法确认所得结论在多大程度上适用于总体.第一步:提出假设检验问题H0:吸烟与患肺癌没有关系↔H1:吸烟与患肺癌有关系第二步:选择检验的指标22()K()()()()n ad bca b c d a c b d-=++++(它越小,原假设“H:吸烟与患肺癌没有关系”成立的可能性越大;它越大,备择假设“H1:吸烟与患肺癌有关系”成立的可能性越大.。

1.2 回归分析课前导引问题导入19世纪德国统计学家恩格尔根据统计资料,对消费结构的变化得出一个规律:一个家庭收入越少,家庭收入中(或总支出中)用来购买食物的支出所占的比例就越大,随着家庭收入的增加,家庭收入中(或总支出中)用来购买食物的支出则会下降.推而广之,一个国家越穷,每个国民的平均收入中(或平均支出中)用于购买食物的支出所占比例就越大,随着国家的富裕,这个比例呈下降趋势.恩格尔系数是根据恩格尔定律得出的比例数,是表示生活水平高低的一个指标.其计算公如下:总支出金额食物支出金额恩格尔系数= 在我国,判定生活发展阶段的标准为:贫困>60%,温饱50%~60%小康40%~50%,富裕<40%据国家统计局统计显示,随着中国经济不断增长,城镇居民家庭恩格尔系数不断下降,恩格尔系数(%) 57.5 54.2 53.8 50.0 48.8 44.7 39.4 37.7 37.1年份 1978 1990 1992 1994 1996 1998 2000 2002 2003求:(1)根据年份预报恩格尔系数的回归方程;(2)预报2006年的恩格尔系数.解析:由于问题中要求根据年份预报恩格尔系数,因此选取年份为自变量x ,恩格尔系数为因变量y ,作散点图如下:(1)由最小二乘法得线性回归方程:yˆ=-0.901 8x +1 845.9 (2)有回归方程可知,2006年的恩格尔系数为-0.901 8×2 006+1 845.9=36.9.知识预览1.回归分析是对有__________的两个变量进行统计分析的常用方法,对两个具有__________关系的变量进行回归分析,我们采用求回归直线方程的方法.2.函数关系是一种__________关系,而相关关系是一种__________关系.3.在回归模型中,y 的值由x 和随机变量ε共同确定,x 称为是__________,ε称为是__________,y 称为是__________,总偏差平方和由__________和__________的总效应组成.4.由部分观测值得到的回归直线,可以对两个变量间的线性相关关系进行估计,这实际上是将__________转化成__________来进行研究.答案:1.相关关系 相关2.确定性 非确定性3.解释变量 随机误差 预报变量 误差平方和 回归平方和4.整体 部分5.对于x , y 随机取到的n 对数据(x i , y i )(i=1,2,…,n),样本相关系数r 的计算公为 ))y n(y )()x n(x ()y -)(y x -(x r n 1i 22i n1i 22i n 1i i i ∑∑∑===--= ))y n(y )()x n(x (y x n y x n 1i 22i n1i 22i n 1i i i∑∑∑===---= r 具有如下性质:(1)|r|≤1;(2)|r|越接近于1,x ,y 的线性相关程度越强;(3)|r|越接近于0,x , y 的线性相关程度越弱.。

独立性检验的基本思想及其初步应用
一、教学目标
1、知识与技能:
通过典型案例的探究,了解独立性检验的基本思想,会对两个分类变量进行独立性检验,明确独立性检验的基本步骤,并能利用独立性检验的基本思想来解决实际问题.
2、过程与方法:
通过探究“吸烟是否与患肺癌有关系”引出独立性检验的问题。
通过列联表、等高条形图,使学生直观感觉到吸烟和患肺癌可能有关系.这一直觉来自于观测数据,即样本.问题是这种来自于样本的印象能够在多大程度上代表总体?这节课就是为了解决这个问题,让学生亲身体验直观感受的基础上,提高学生的数据分析能力.
3、情感态度价值观:
通过本节课的学习,加强数学与现实生活的联系。
以科学的态度评价两个分类变量有关系的可能性。
培养学生运用所学知识,解决实际问题的能力。
对问题的自主探究,提高学生独立思考问题的能力;让学生对统计方法有更深刻的认识,体会统计方法应用的广泛性,进一步体会科学的严谨性。
教学中适当地利用学生合作与交流,使学生在学习的同时,体会与他人合作的重要性。
二、教学重点
理解独立性检验的基本思想及实施步骤.
三、教学难点
1.了解独立性检验的基本思想;
2.了解随机变量K2的含义,K2的观测值很大,就认为两个分类变量是有关系的。
四、教学方法
以“问题串”的形式,层层设疑,诱思探究。
用“讲授法”,循序渐进,引导学生,步步为营,螺蜁上升探究本节课的知识内容.
五、教学过程设计。
独立性检验(一)
教学目标:
1, 了解独立性检验的含义,理解22⨯列联表。
2, 会用统计量判断两系。
3, 通过典型案例,掌握独立性检验的基本思想。
课前预习
1用样本估计总体时,由于抽样的随机性,由样本得到的推断不一定正确。
利用2
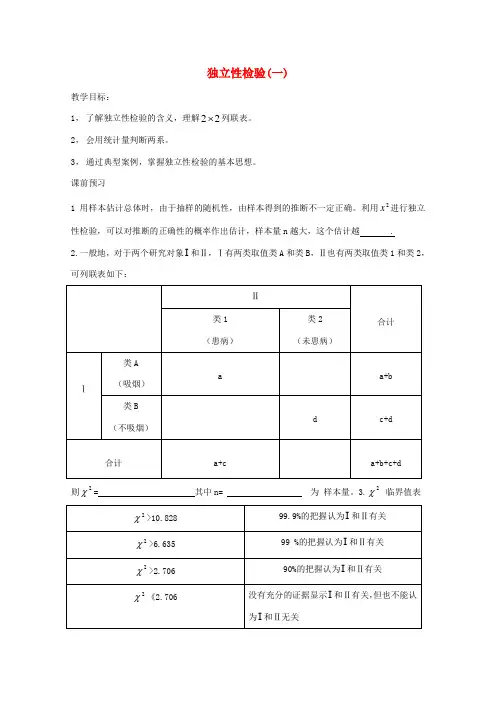
x 进行独立性检验,可以对推断的正确性的概率作出估计,样本量n 越大,这个估计越 . 2.一般地,对于两个研究对象I 和Ⅱ,Ⅰ有两类取值类A 和类B ,Ⅱ也有两类取值类1和类2,可列联表如下:
则2
χ= 其中n= 为 样本量。
3.2
χ 临界值表
例1. 在500人身上试验某种,把他们一年中的感冒记录与另外500名未用血清的人的感冒记录作比较,结果如表1—1—5所示。
问:该种血清能否起到预防感冒的作用?
表1—1—5
例2.考查人的高血压是否与食盐摄入量有关,对某地区人群进行跟踪调查,得到以下数据:
1.某桑场为了了解职工发生工作人员进行了一次调查,结果如下表。
试问:发生皮炎是否与
采桑有关?
2.为了鉴定新疫苗的效力,将60只豚鼠随机地分成两组,在其中一组接种疫苗后,两组都注射了病源菌,结果列于下表。
问:能否有90%的把握认为疫苗有效?
3某医疗研究机构为了了解关系,进行了一次抽样调查,得到如下数据。
问:打鼾与患心脏病是否有关?。

1.1 独立性检验(共计5课时)一、教学内容与教学对象分析通过典型案例,学习下列一些常用的统计方法,并能初步应用这些方法解决一些实际问题。
通过对典型案例(如“患肺癌与吸烟有关吗”等)的探究。
了解独立性检验(只要求2×2列联表)的基本思想、方法及初步应用。
二. 学习目标1、知识与技能通过本节知识的学习,了解独立性检验的基本思想和初步应用,能对两个分类变量是否有关做出明确的判断。
明确对两个分类变量的独立性检验的基本思想具体步骤,会对具体问题作出独立性检验。
2、过程与方法在本节知识的学习中,应使学生从具体问题中认识进行独立性检验的作用及必要性,树立学好本节知识的信心,在此基础上学习三维柱形图和二维柱形图,并认识它们的基本作用和存在的不足,从而为学习下面作好铺垫,进而介绍K的平方的计算公式和K的平方的观测值R的求法,以及它们的实际意义。
从中得出判断“X与Y有关系”的一般步骤及利用独立性检验来考察两个分类变量是否有关系,并能较准确地给出这种判断的可靠程度的具体做法和可信程度的大小。
最后介绍了独立性检验思想的综合运用。
3、情感、态度与价值观通过本节知识的学习,首先让学生了解对两个分类博变量进行独立性检验的必要性和作用,并引导学生注意比较与观测值之间的联系与区别,从而引导学生去探索新知识,培养学生全面的观点和辨证地分析问题,不为假想所迷惑,寻求问题的内在联系,培养学生学习数学、应用数学的良好的数学品质。
加强与现实生活相联系,从对实际问题的分析中学会利用图形分析、解决问题及用具体的数量来衡量两个变量之间的联系,学习用图形、数据来正确描述两个变量的关系。
明确数学在现实生活中的重要作用和实际价值。
教学中,应多给学生提供自主学习、独立探究、合作交流的机会。
养成严谨的学习态度及实事求是的分析问题、解决问题的科学世界观,并会用所学到的知识来解决实际问题。
三.教学重点、难点教学重点:理解独立性检验的基本思想;独立性检验的步骤。

苏教版高中数学(选修1-2)重难点突破全册知识点梳理及重点题型举一反三巩固练习独立性检验的基本思想及其初步应用【学习目标】1. 了解独立性检验(只要求2×2列联表)的基本思想、方法及初步应用2. 通过典型案例的探究,了解实际推断原理和假设检验的基本思想、方法及初步应用.【要点梳理】要点一、分类变量有一种变量,这种变量所取不同的“值”表示的是个体所属不同类别,称这种变量为分类变量。
要点诠释:(1)对分类变量的理解。
这里的“变量”和“值”都应作为广义的“变量”和“值”进行理解。
例如:“性别变量”有“男”和“女”两种类别,这里的变量指的是性别,同样这里的“值”指的是“男”和“女”。
因此,这里所说的“变量”和“值”取的不一定是具体的数值。
(2)分类变量可以有多种类别。
例如:吸烟变量有“吸烟”与“不吸烟”两种类别,而国籍变量则有多种类别。
要点二、2×2列联表1. 列联表用表格列出的分类变量的频数表,叫做列联表。
2. 2×2列联表对于两个事件A,B,列出两个事件在两种状态下的数据,如下表所示:这样的表格称为2×2列联表。
要点三:卡方统计量公式为了研究分类变量X与Y的关系,经调查得到一张2×2列联表,如下表所示统计中有一个有用的(读做“卡方”)统计量,它的表达式是:22()()()()()n ad bc K a b c d a c b d -=++++(n a b c d =+++为样本容量)。
要点四、独立性检验1. 独立性检验通过2×2列联表,再通过卡方统计量公式计算2K 的值,利用随机变量2K 来确定在多大程度上可以认为“两个分类变量有关系”的方法称为两个分类变量的独立性检验。
2. 变量独立性的判断通过对2K 统计量分布的研究,已经得到两个临界值:3.841和6.635。
当数据量较大时,在统计中,用以下结果对变量的独立性进行判断:①如果2K ≤3.841时,认为事件A 与B 是无关的。
回归分析的基本思想及其初步应用【教学目标】:(1)知识与技能:了解回归模型的选择;进一步理解非线性模型通过变换转化为线性回归模型;体会不同模型拟合数据的效果。
(2)过程与方法:从实例出发,求出相应的回归直线方程,从中也找出存在的不足,从而有进行回归分析的必要性,通过学习相关指数,用相关指数来刻画回归的效果,进而归纳出回归分析的一般步骤,并对具体问题进行回归分析,用于解决实际问题。
(3)情感态度与价值观:任何事物都是相对的,但又有一定的规律性,我们只要从实际出发,不断探求事物的内在联系,就会找出其中的规律性,形成解决实际问题的方法和能力。
【教学重点】:1.加深体会有些非线性模型通过变换可以转化为线性回归模型;2.了解在解决问题的过程中寻找更好的模型的方法。
【教学难点】:1.了解常用函数的图像特点,选择不同的模型建模;2.通过比较相关指数对不同的模型进行比较。
教学过程问题导学一、求线性回归方程活动与探究1某工厂1~8月份某种产品的产量与成本的统计数据见下表:以产量为x,成本为y.(1)画出散点图;(2)y与x是否具有线性相关关系?若有,求出其回归方程.迁移与应用1.(2013海南海口模拟)在一次试验中,测得(x,y)的四组值分别是A(1,2),B(2,3),C(3,4),D(4,5),则y与x之间的回归直线方程为()A.=x+1 B.=x+2C.=2x+1 D.=x-12.某商场经营一批进价是30元/台的小商品,在市场试验中发现,此商品的销售单价x(x取整数)元与日销售量y台之间有如下关系:(1)y与x是否具有线性相关关系?如果具有线性相关关系,求出回归直线方程.(方程的斜率精确到个位)(2)设经营此商品的日销售利润为P元,根据(1)写出P关于x的函数关系式,并预测当销售单价x为多少元时,才能获得最大日销售利润.(1)散点图是定义在具有相关关系的两个变量基础上的,对于性质不明确的两组数据,可先作散点图,在图上看它们有无关系,关系的密切程度,然后再进行相关回归分析.(2)求回归直线方程,首先应注意到,只有在散点图大致呈线性时,求出的回归直线方程才有实际意义,否则,求出的回归直线方程毫无意义.二、线性回归分析活动与探究2某运动员训练次数与运动成绩之间的数据关系如下:(1)作出散点图;(2)求出线性回归方程;(3)作出残差图,并说明模型的拟合效果;(4)计算R2,并说明其含义.迁移与应用1.某产品的广告费用x与销售额y的统计数据如下表:根据上表可得回归方程=x+中的为9.4,据此模型预报广告费用为6万元时销售额为()A.63.6万元B.65.5万元C.67.7万元D.72.0万元2.在一段时间内,某种商品的价格x(元)和需求量y(件)之间的一组数据为:且知x与y具有线性相关关系,求出y对x的回归直线方程,并说明拟合效果的好坏.“相关指数R2、残差图”在回归分析中的作用:(1)相关指数R2是用来刻画回归效果的,由R2=1-可知R2越大,意味着残差平方和越小,也就是说模型的拟合效果就越好.(2)残差图也是用来刻画回归效果的,判断依据是:残差点比较均匀地分布在水平带状区域中,带状区域越窄,说明模型拟合精度越高,回归方程预报精度越高.三、非线性回归分析活动与探究3下表为收集到的一组数据:(1)作出x与y的散点图,并猜测x与y之间的关系;(2)建立x与y的关系,预报回归模型并计算残差;(3)利用所得模型,预报x=40时y的值.迁移与应用1.在彩色显影中,由经验知形成染料光学密度y与析出银的光学密度x由公式y=e b xA(b<0)表示,现测得试验数据如下:则y对x的回归方程是__________.2.在一次抽样调查中测得样本的5个样本点,数值如下表:试建立y与x之间的回归方程.非线性回归问题有时并不给出经验公式,这时我们可以画出已知数据的散点图,把它与学过的各种函数(幂函数、指数函数、对数函数等)图象作比较,挑选一种跟这些散点拟合得最好的函数,然后采用适当的变量置换,把问题化为线性回归分析问题,使之得到解决.[答案] 课前·预习导学 【预习导引】1.(1)确定性 非确定性 (2)相关 (3) =1221ni ii n i i x ynx yx nx==--∑∑ -样本点的中心 (4)随机误差 解释变量 预报变量 预习交流1 D2.y i -bx i -a y i -i y i -x i -3.1- 解释变量 预报变量 1预习交流2 提示:散点图可以说明变量间有无线性相关关系,只能粗略地说明两个变量之间关系的密切程度,而相关指数R 2能精确地描述两个变量之间的密切程度.预习交流3 提示:(1)回归方程只适用于所研究的样本的总体. (2)所建立的回归方程一般都有时间性. (3)样本的取值范围会影响回归方程的适用范围.(4)不能期望回归方程得到的预报值就是预报变量的精确值.事实上,它是预报变量的可能取值的平均值.课堂·合作探究 【问题导学】活动与探究1 思路分析:画出散点图,观察图形的形状得x 与y 是否具有线性相关关系.把数值代入回归系数公式求回归方程.解:(1)由表画出散点图,如图所示.(2)从上图可看出,这些点基本上散布在一条直线附近,可以认为x 和y 线性相关关系显著,下面求其回归方程,首先列出下表.=6.85,=157.25.∴=81822188i ii ii x yx yxx ==--∑∑=≈22.17, =-=157.25-22.17×6.85≈5.39,故线性回归方程为=22.17x +5.39. 迁移与应用 1.A [解析]方法一:==,==.故===1,=-=-=1.因此,=x+1,故选A.方法二:也可由回归直线方程一定过点(,),即,代入验证可排除B,C,D.故应选A.2.[解析](1)散点图如图所示,从图中可以看出这些点大致分布在一条直线附近,因此两个变量线性相关.设回归直线为=x+,由题知=42.5,=34,则求得==≈-3.=-=34-(-3)×42.5=161.5.∴=-3x+161.5.(2)依题意有P=(-3x+161. 5)(x-30)=-3x2+251.5x-4 845=-32+-4 845.∴当x=≈42时,P有最大值,约为426.即预测销售单价为42元时,能获得最大日销售利润.活动与探究2思路分析:先画出散点图,确定是否具有线性相关关系,求出回归方程,再求出残差,确定模型的拟合的效果和R2的含义.[解析](1)作出该运动员训练次数(x)与成绩(y)之间的散点图,如图所示,由散点图可知,它们之间具有线性相关关系.(2) =39.25,=40.875,=12 656,=13 731,y i=13 180,i∴==≈1.041 5,=-=-0.003 875,∴线性回归方程为=1.041 5x-0.003 875.(3)作残差图如图所示,由图可知,残差点比较均匀地分布在水平带状区域中,说明选用的模型比较合适.(4)计算得相关指数R2≈0.985 5,说明了该运动员的成绩的差异有98.55%是由训练次数引起的.迁移与应用1.B[解析]∵=-=-9.4×=9.1,∴回归方程为=9.4x +9.1.令x =6,得=9.4×6+9.1=65.5(万元). 2.[解析]=×(14+16+18+20+22)=18,=×(12+10+7+5+3)=7.4,521ii x=∑=142+162+182+202+222=1 660,521ii y=∑=122+102+72+52+32=327,i y i =14×12+16×10+18×7+20×5+22×3=620,∴=51522155i ii ii x yx y xx ==--∑∑===-1.15.∴=7.4+1.15×18=28.1,∴回归直线方程为=-1.15x +28.1. 列出残差表为:∴(y i -i )2=0.3, (y i -)2=53.2,R 2=1-≈0.994.故R 2≈0.994说明拟合效果较好.活动与探究3 思路分析:先由数值表作出散点图,然后根据散点的形状模拟出近似函数,进而转化为线性函数,由数值表求出回归函数.[解析](1)作出散点图如图,从散点图可以看出x 与y 不具有线性相关关系,根据已有知识可以发现样本点分布在某一条指数函数曲线21e c x y c =的周围,其中c 1,c 2为待定的参数.(2)对两边取对数把指数关系变为线性关系,令z =ln y ,则有变换后的样本点应分布在直线z =bx +a ,a =ln c 1,b =c 2的周围,这样就可以利用线性回归模型来建立y 与x 之间的非线性回归方程了,数据可以转化为:求得回归直线方程为=0.272x -3.849,∴=e 0.272x -3.849.残差(3)当x =40时,y =e 0.272x -3.849≈1 131.迁移与应用 1.$0.151.73e xy -= [解析]由题给的经验公式y =e b x A ,两边取自然对数,便得ln y =ln A +.与线性回归直线方程相对照,只要取u =,v =ln y ,a =ln A ,就有v =a +bu ,这是v 对u 的线性回归方程.对此我们已经掌握了一套相关性检验,求a 与回归系数b 的方法.题目所给数据经变量置换u =,v =ln y 变成如下表所示的数据:|r |≈0.998>0.75,故v与u之间具有很强的线性相关关系,求回归直线方程是有意义的.由表中数据可得≈-0.15,≈0.55,即=0.55-0.15u.把u与v换回原来的变量x与y,即u=,v=ln y,故ln =0.55-,即=0.150.55e x-=e0.550.15e x-≈0.151.73e x-.这就是y对x的回归曲线方程.2.[解析]画出散点图如图所示.根据散点图可知y与x近似地呈反比例函数关系,设y=,令t=,则y=kt,原数据变为:由置换后的数值表作散点图如下:由散点图可以看出y与t呈近似的线性相关关系.列表如下:所以=1.55,=7.2.所以=≈4.134 4,=-≈0.8.所以=4.134 4t+0.8.所以y与x的回归方程是=+0.8.当堂检测1.(2012湖南高考,理4)设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(x i,y i)(i=1,2,…,n),用最小二乘法建立的回归方程为$y =0.85x-85.71,则下列结论中不正确的是()A.y与x具有正的线性相关关系B.回归直线过样本点的中心(x,y)C.若该大学某女生身高增加1 cm,则其体重约增加0.85 kgD.若该大学某女生身高为170 cm,则可断定其体重必为58.79 kg[答案]D[解析]D选项中,若该大学某女生身高为170 cm,则可断定其体重约为0.85×170-85.71=58.79(kg).故D不正确.3.为了解儿子身高与其父亲身高的关系,随机抽取5对父子的身高数据如下:则y对x的线性回归方程为()A.y=x-1 B.y=x+1C .y =88+12xD .y =176[答案]C[解析]法一:由线性回归直线方程过样本中心(176,176),排除A ,B[答案],结合选项可得C 为正确[答案].法二:将表中的五组数值分别代入选项验证,可知y =88+12x最适合.3.在两个变量y 与x 的回归模型中,分别选择了4个不同的模型.通过计算得R 2的值如下,其中拟合效果最好的模型是( )A .模型1的R 2为0.98B .模型2的R 2为0.80C .模型3的R 2为0.50D .模型4的R 2为0.25 [答案]A[解析]R 2越接近于1,则该模型的拟合效果就越好,精度越高.4.若对于变量y 与x 的10组统计数据的回归模型中,R 2=0.95,又知残差平方和为120.53,那么101i =∑(y i -y )2的值为______.[答案]2 410.6[解析]依题意有0.95=1-1021120.53()ii y y =-∑,所以1021()ii yy =-∑=2 410.6.4. 假设关于某设备的使用年限x (年)和所支出的维修费用y (万元)有如下的统计数据.若由此资料可知y 对x 呈线性相关关系,试求: (1)回归直线方程;[解析]由题表中数据列成下表:于是51522215112.35451.2390545i ii ii x y x ybxx ==--⨯⨯===-⨯-∑∑$,$a=y -bx $=5-1.23×4=0.08, 所以回归直线方程为$y=bx $+$a =1.23x +0.08.(2)估计使用年限为10年时,维修费用为多少? [答案]当x =10时,$y=1.23×10+0.08=12.38(万元),估计使用10年时的维修费用为12.38万元. 课堂小结:(学生总结) 板书设计:(略) 教后记:。
1.1独立性检验的基本思想及其初步应用●三维目标1.知识与技能了解独立性检验的基本思想、方法及初步应用.会从列联表(只要求2×2列联表)、柱形图、条形图直观分析两个分类变量是否有关.会用K2公式判断两个分类变量在某种可信程度上的相关性.2.过程与方法运用数形结合的方法,借助对典型案例的探究,来了解独立性检验的基本思想,总结独立性检验的基本步骤.3.情感、态度与价值观(1)通过本节课的学习,让学生感受数学与现实生活的联系,休会独立性检验的基本思想在解决日常生活问题中的作用.(2)培养学生运用所学知识,依据独立性检验的思想作出合理推断的实事求是的好习惯.●重点难点重点:理解独立性检验的基本思想及实施步骤.难点:了解独立性检验的基本思想、了解随机变量K2的含义.分别利用2×2列联表、等高条形图、K2公式分析两变量之间的关系,探究解题方法和规律,充分理解观测值k的意义,能熟练正确地对问题作出判断,达到化难为易的目的.●教学建议通过对典型案例“吸烟是否对患肺癌有影响?”的提出,联系生活,引起共鸣,激发学生的学习兴趣.从生活的实例出发,让学生充分体会数学与实际生活的联系,从而使得本节知识的形成更自然、更生动.要注重学生的主体参与,努力创设教师引导下的学生自主探究、合作交流的学习方式.建议在教学过程中,教师点拨、学生探讨,共同完成例题的解答.要注重数学的思想性,采用反证法做类比,帮助学生理解独立性检验的思想,通过课堂练习,检验学生能否熟练掌握用独立性检验思想解决实际问题的方法.●教学流程通过典型案例“吸烟是否与患肺癌有关系”的研究,介绍了独立性检验的基本思想、方法和初步应用.创设问题情境引出列联表、等高条形图和K2公式等基础知识.利用填一填的形式,使学生自主学习本节基础知识,并反馈了解,对理解有困难的概念加以讲解.引导学生在学习基础知识的基础上分析解决例题1的问题,并总结规律方法,完成变式训练.引导学生分析例题2,根据图中的数据计算出各类变量对应的频率,作出等宽且高度均为1的条形图.并通过图形作出判断,完成变式训练.完成当堂双基达标,巩固所学知识及应用方法,并进行反馈矫正.归纳整理,进行课堂小结,整体认识本节所学知识,强调重点内容和规律方法.要求学生借鉴例题3的解法完成变式训练.给出易错辨析题目及错解,让学生讨论错因,并给出正确解答.引导学生探究例题3的解法,(1)直接由表中数据代入公式,作出判断.(2)列出列联表,由公式计算观测值,作出判断.解后让学生总结规律方法.课标解读1.了解独立性检验的基本思想、方法及其简单应用.(重点)2.通过收集数据,并依据独立性检验的原理作出合理推断,培养学生良好的思维习惯.(难点)分类变量与列联表吸烟变量有几种类别?国籍变量呢?【提示】吸烟变量有吸烟与不吸烟两种类别,而国籍变量则有多种类别,如中国、美国、法国…….1.分类变量变量的不同“值”表示个体所属的不同类别,像这样的变量称为分类变量.2.列联表(1)定义:列出的两个分类变量的频数表,称为列联表.(2)2×2列联表:一般地,假设有两个分类变量X和Y,它们的取值分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为:2×2列联表y1y2总计x1 a b a+bx 2 c d c +d 总计a +cb +da +b +c +d等高条形图【问题导思】表格和图形哪一个更能直观地反映出两个分类变量间是否相互影响? 【提示】 图形.(1)定义:将列联表中的数据用高度相同的两个条形图表示出来,其中两列的数据分别对应不同的颜色,这就是等高条形图.(2)特征:等高条形图与表格相比,更能直观地反映出两个分类变量间是否相互影响,常用等高条形图展示列联表数据的频率特征.(3)用法:观察等高条形图发现a a +b 和cc +d 相差很大,就判断两个分类变量之间有关系.独立性检验(1)定义:利用随机变量K 2来判断“两个分类变量有关系”的方法称为独立性检验. (2)公式:K 2=n ad -bc 2a +bc +d a +cb +d,其中n =a +b +c +d 为样本容量.用2×2列联表分析两变量间的关系在对人们饮食习惯的一次调查中,共调查了124人,其中六十岁以上的70人,六十岁以下的54人.六十岁以上的人中有43人的饮食以蔬菜为主,另外27人则以肉类为主;六十岁以下的人中有21人饮食以蔬菜为主,另外33人则以肉类为主.请根据以上数据作出饮食习惯与年龄的列联表,并利用a a +b 与cc +d判断二者是否有关系.【思路探究】 对变量进行分类→求出分类变量的不同取值→作出2×2列联表→计算a a +b 与c c +d的值作出判断 【自主解答】 2×2列联表如下:年龄在六年龄在六总计十岁以上十岁以下 饮食以蔬菜为主 43 21 64 饮食以肉类为主 27 33 60 总计7054124将表中数据代入公式得 a a +b =4364=0.671 875. c c +d =2760=0.45. 显然二者数据具有较为明显的差距,据此可以在某种程度上认为饮食习惯与年龄有关系.1.作2×2列联表时,注意应该是4行4列,计算时要准确无误. 2.作2×2列联表时,关键是对涉及的变量分清类别.题中条件不变,尝试用|ad -bc|的大小判断饮食习惯与年龄是否有关. 【解】 将本例2×2列联表中的数据代入可得 |ad -bc|=|43×33-21×27|=852.相差较大,可在某种程度上认为饮食习惯与年龄有关系.用等高条形图分析两变量间的关系某学校对高三学生作了一项调查,发现:在平时的模拟考试中,性格内向的学生426人中有332人在考前心情紧张,性格外向的学生594人中有213人在考前心情紧张.作出等高条形图,利用图形判断考前心情紧张与性格类别是否有关系.【思路探究】 作出2×2列联表―→根据列联表数据 作等高条形图―→对比乘积的差距判断两 个分类变量是否有关【自主解答】 作列联表如下:性格内向 性格外向 总计 考前心情紧张 332 213 545 考前心情不紧张 94 381 475 总计4265941 020图中阴影部分表示考前心情紧张与考前心情不紧张中性格内向的比例.从图中可以看出,考前紧张的样本中性格内向占的比例比考前心情不紧张样本中性格内向占的比例高,可以认为考前紧张与性格类型有关.1.利用列联表中数据计算出各类变量取值对应频率,作出等宽度且高度均为1的等高条形图.2.利用数形结合的思想,借助等高条形图来判断两个分类变量是否相关是判断变量相关的常见方法之一.一般地,在等高条形图中,a a +b 与c c +d 相差越大,两个分类变量有关系的可能性就越大.作等高条形图时可以用列联表来寻找相关数据,作图要精确,且易于观察,使对结论的判断不出现偏差.某生产线上,质量监督员甲在生产现场时,990件产品中有合格品982件,次品8件;不在生产现场时,510件产品中有合格品493件,次品17件.试利用图形判断监督员甲在不在生产现场对产品质量好坏有无影响.【解】 根据题目所给数据得如下2×2列联表:合格品数 次品数 总计 甲在生产现场 982 8 990 甲不在生产现场 493 17 510 总计1 475251 500图中两个深色条的高分别表示甲在生产现场和甲不在生产现场样本中次品数的频率.从图中可以看出,甲不在生产现场样本中次品数的频率明显高于甲在生产现场样本中次品数的频率.因此可以认为质量监督员甲在不在生产现场与产品质量好坏有关系.独立性检验下表是某地区的一种传染病与饮用水的调查表:得病 不得病 总计 干净水 52 466 518 不干净水 94 218 312 总计146684830(1)这种传染病是否与饮用水的卫生程度有关,请说明理由;(2)若饮用干净水得病的有5人,不得病的有50人,饮用不干净水得病的有9人,不得病的有22人.按此样本数据分析这种疾病是否与饮用水有关,并比较两种样本在反映总体时的差异.【思路探究】 求出k 2的值―→与临界值作比较―→作出判断.【自主解答】 (1)假设H 0:传染病与饮用水无关.把表中数据代入公式得: K 2的观测值k =830×52×218-466×942146×684×518×312≈54.21.在H 0成立的情况下,P(K 2>10.828)≈0.001,是小概率事件, 所以拒绝H 0.因此我们有99.9%的把握认为该地区这种传染病与饮用不干净水有关. (2)依题意得2×2列联表:得病 不得病 总计 干净水 5 50 55 不干净水 9 22 31 总计147286此时,K 2的观测值k =86×5×22-50×9214×72×55×31≈5.785.因为5.785>5.024,P(K 2>5.024)≈0.025,所以我们有97.5%的把握认为该种疾病与饮用不干净水有关.两个样本都能统计得到传染病与饮用不干净水有关这一相同结论,但(1)中我们有99.9%的把握肯定结论的正确性,(2)中我们只有97.5%的把握肯定.解决一般的独立性检验问题的步骤:(1)通过列联表确定a 、b 、c 、d 、n 的值,根据实际问题需要的可信程度确定临界值k 0;(2)利用K 2=n ad -bc 2a +bc +d a +cb +d求出K 2的观测值k ;(3)如果k≥k 0,就推断“两个分类变量有关系”,这种推断犯错误的概率不超过α;否则就认为在犯错误的概率不超过α的前提下不能推断“两个分类变量有关系”.某社区医疗服务部门为了考察人的高血压病是否与食盐摄入量有关,对该社区的1 633人进行了跟踪测查,得出以下数据:患高血压 未患高血压 合计 喜欢较咸食物 34 220 254 喜欢清淡食物 26 1 353 1 379 合计601 5731 633问能否判断在犯错误的概率不超过0.001的前提下,认为患高血压与食盐摄入量有关? 【解】 提出假设H 0:该社区患有高血压病与食盐的摄入量无关. 由公式计算K 2的观测值为 k =1 633×34×1 353-220×26260×1 573×254×1 379≈80.155.因为80.155>10.828,因此在犯错误的概率不超过0.001的前提下,我们认为该社区患有高血压病与食盐的摄入量有关.因未理解P(K 2≥k 0)的含义而致误某小学在对232名小学生调查中发现:180名男生中有98名有多动症,另外82名没有多动症,52名女生中有2名有多动症,另外50名没有多动症,用独立性检验方法判断多动症与性别是否有关系?【错解】 由题目数据列出如下列联表:多动症 无多动症 总计 男生 98 82 180 女生 2 50 52 总计100132232k =232×98×50-2×82100×132×180×52≈42.117>10.828.所以有0.1%的把握认为多动症与性别有关系.【错因分析】 应该是有(1-P(K 2≥10.828))×100%=(1-0.001)×100%的把握,而不是P(K 2≥10.828)×100%=0.001×100%的把握.【防范措施】 本题的错误之处在于不能正确理解独立性检验步骤的含义,当计算的K 2的观测值k 大于临界值k 0时,就可推断在犯错误的概率不超过α的前提下说两分类变量有关系.这一点需牢记,才能避免类似错误.【正解】 由题目数据列出如下列联表:多动症 无多动症 总计 男生 98 82 180 女生 2 50 52 总计100132232由表中数据可得到: k =232×98×50-2×822100×132×180×52≈42.117>10.828.所以有99.9%的把握认为多动症与性别有关系.1.列联表与等高条形图列联表由两个分类变量之间频率大小差异说明这两个变量之间是否有关联关系,而利用等高条形图能形象直观地反映它们之间的差异,进而推断它们之间是否具有关联关系.2.对独立性检验思想的理解独立性检验的基本思想类似于数学中的反证法.先假设“两个分类变量没有关系”成立,计算随机变量K2的值,如果K2值很大,说明假设不合理.K2越大,两个分类变量有关系的可能性越大.1.在研究吸烟与患肺癌的关系中,通过收集数据、整理分析数据得“吸烟与患肺癌有关”的结论,并且在犯错误的概率不超过0.01的前提下认为这个结论是成立的,下列说法中正确的是()A.100个吸烟者中至少有99人患有肺癌B.1个人吸烟,那么这个人有99%的概率患有肺癌C.在100个吸烟者中一定有患肺癌的人D.在100个吸烟者中可能一个患肺癌的人也没有【解析】独立性检验的结果与实际问题有差异,即独立性检验的结论是一个数学统计量,它与实际问题中的确定性存在差异.【答案】 D2.分类变量X和Y的列联表如下,则()y1y2总计x1 a b a+bx2 c d c+d总计a+c b+d a+b+c+dA.ad-bcB.ad-bc越大,说明X与Y的关系越强C.(ad-bc)2越大,说明X与Y的关系越强D.(ad-bc)2越接近于0,说明X与Y的关系越强【解析】由K2的计算公式可知,(ad-bc)2越大,则K2越大,故相关关系越强.【答案】 C3.观察下列各图,其中两个分类变量x、y之间关系最强的是()【解析】 在四幅图中,D 图中两个深色条的高相差最明显,说明两个分类变量之间关系最强.【答案】 D4.为了探究患慢性气管炎是否与吸烟有关,调查了339名50岁以上的人,调查结果如下表所示:患慢性气管炎 未患慢性气管炎 合计 吸烟 43 162 205 不吸烟 13 121 134 合计56283339【解】 从题目的2×2列联表中可知:a =43,b =162,c =13,d =121,a +b =205,c +d =134,a +c =56,b +d =283,n =a +b +c +d =339,代入公式:K 2=n ad -bc 2a +bc +d a +cb +d ,得k =339×43×121-162×132205×134×56×283≈7.469.因为7.469>6.635,所以我们有99%的把握认为50岁以上的人患慢性气管炎与吸烟习惯有关系.一、选择题1.有两个分类变量X 与Y 的一组数据,由其列联表计算得k≈4.523,则认为“X 与Y 有关系”犯错误的概率为( )A .95%B .90%C .5%D .10%【解析】 P(K 2≥3.841)≈0.05,而k≈4.523>3.841.这表明认为“X 与Y 有关系”是错误的可能性约为0.05,即认为“X 与Y 有关系”犯错误的概率为5%.【答案】 C2.在一项中学生近视情况的调查中,某校男生150名中有80名近视,女生140名中有70名近视,在检验这些中学生眼睛近视是否与性别有关时用什么方法最有说服力( )A .平均数与方差B .回归分析C .独立性检验D .概率【解析】 判断两个分类变量是否有关的最有效方法是进行独立性检验,故选C. 【答案】 C3.利用独立性检验来考虑两个分类变量X 和Y 是否有关系时,通过查阅临界值表来确定推断“X 与Y 有关系”的可信度,如果k >5.024,那么就推断“X 和Y 有关系”,这种推断犯错误的概率不超过( )A.0.25 B.0.75C.0.025 D.0.975【解析】∵P(k>5.024)=0.025,故在犯错误的概率不超过0.025的条件下,认为“X 和Y有关系”.【答案】 C4.下面是调查某地区男女中学生喜欢理科的等高条形图,阴影部分表示喜欢理科的百分比,从图中可以看出()图1-2-1A.性别与喜欢理科无关B.女生中喜欢理科的比为80%C.男生比女生喜欢理科的可能性大些D.男生不喜欢理科的比为60%【解析】本题考查学生的识图能力,从图中可以分析,男生喜欢理科的可能性比女生大一些.【答案】 C5.在调查中发现480名男人中有38名患有色盲,520名女人中有6名患有色盲.下列说法正确的是()A.男、女患色盲的频率分别为0.038,0.006B.男、女患色盲的概率分别为19240,3 260C.男人中患色盲的比例比女人中患色盲的比例大,患色盲与性别是有关的D.调查人数太少,不能说明色盲与性别有关【解析】男人中患色盲的比例为38480,要比女人中患色盲的比例6520大,其差值为|38480-6520|≈0.0 676,差值较大.【答案】 C二、填空题6.某班主任对全班50名学生作了一次调查,所得数据如表:认为作业多认为作业不多总计喜欢玩电脑游戏 18 9 27 不喜欢玩电脑游戏 8 15 23 总计262450在犯错误的概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关.【解析】 查表知若要在犯错误的概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关,则临界值k 0=6.635.本题中,k≈5.059<6.635,所以不能在犯错误的概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关.【答案】 不能7.独立性检验所采用的思路是:要研究A ,B 两类型变量彼此相关,首先假设这两类变量彼此________.在此假设下构造随机变量K 2,如果K 2的观测值较大,那么在一定程度上说明假设________.【答案】 无关 不成立8.某高校《统计初步》课程的教师随机调查了选该课的一些学生的情况,具体数据如下表:专业性别 非统计专业 统计专业 男生 13 10 女生720K 2的观测值为k =50×13×20-10×7223×27×20×30≈4.844.因为k >3.841,所以确认“主修统计专业与性别有关系”,这种判断出现错误的可能性为________.【解析】 因为随机变量K 2的观测值k >3.841,所以在犯错误的概率不超过0.05的前提下认为“主修统计专业与性别有关系”.故这种判断出现错误的可能性为5%.【答案】 5%三、解答题9.为了探究学生选报文、理科是否与对外语的兴趣有关,某同学调查了361名高二在校学生,调查结果如下:理科对外语有兴趣的有138人,无兴趣的有98人,文科对外语有兴趣的有73人,无兴趣的有52人.试分析学生选报文、理科与对外语的兴趣是否有关?【解】 列出2×2列联表理 文 总计 有兴趣 138 73 211 无兴趣9852150总计236 125 361代入公式得K 2的观测值 k =361×138×52-73×982236×125×211×150≈1.871×10-4.∵1.871×10-4<2.706,∴可以认为学生选报文、理科与对外语的兴趣无关.10.某校对学生课外活动进行调查,结果整理成下表:运用你所学过的知识进行分析,能否在犯错误的概率不超过0.005的前提下,认为“喜欢体育还是文娱与性别有关系”?体育 文娱 合计 男生 21 23 44 女生 6 29 35 合计275279【解】由图可以直观地看出喜欢体育还是喜欢文娱与性别在某种程度上有关系,但只能作粗略判断,具体判断方法如下:假设“喜欢体育还是喜欢文娱与性别没有关系”, ∵a =21,b =23,c =6,d =29,n =79, ∴K 2的观测值为k =79×21×29-23×6221+23×6+29×21+6×23+29≈8.106.且P(K 2≥7.879)≈0.005,即我们得到的K 2的观测值k≈8.106超过7.879,这就意味着:“喜欢体育还是文娱与性别没有关系”这一结论成立的可能性小于0.005,即在犯错误的概率不超过0.005的前提下认为“喜欢体育还是喜欢文娱与性别有关”.11.某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表:甲厂:分组[29.86,29.90) [29.90, 29.94) [29.94, 29.98) [29.98, 30.02) [30.02, 30.06) [30.06, 30.10) [30.10, 30.14) 频数12638618292614分组 [29.86, 29.90) [29.90, 29.94) [29.94, 29.98) [29.98, 30.02) [30.02, 30.06) [30.06, 30.10) [30.10, 30.14) 频数297185159766218(2)由以上统计数据填下面2×2列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.甲厂 乙厂 合计 优质品 非优质品 合计附:K 2=n ad -bc a +bc +d a +cb +dP(K 2≥k) 0.05 0.01 k3.8416.635 【解】 (1)为360500=72%; 乙厂抽查的产品中有320件优质品,从而乙厂生产的零件的优质品率估计为320500=64%.(2)甲厂 乙厂 合计 优质品 360 320 680 非优质品 140 180 320 合计5005001 000k =1 000×360×180-320×1402500×500×680×320≈7.353>6.635,因此,在犯错误的概率不超过0.01的前提下,即有99%的把握认为“两个分厂生产的零件的质量有差异”.在对人们休闲方式的调查中,已知男性占总调查人数的25,其中有一半的休闲方式是运动,而女性只有13的休闲方式是运动.经过调查员计算,在犯错误的概率不超过0.05的前提下,可认为“性别与休闲方式有关”,那么被调查的人中最少有多少人的休闲方式是运动?【思路探究】 (1)设总共调查了n 人,则其中男性有多少人?其中休闲方式为运动的有多少人?非运动的呢?(2)被调查的女性有多少人?休闲方式是运动的有多少人?非运动的呢? (3)根据题意,K 2的临界值为多少?K 2的观测值为多少?二者之间有什么关系? 【自主解答】 设总共调查n 人,则被调查的男性人数应为25n ,其中有n5人的休闲方式是运动;被调查的女性人数应为3n 5,其中有n5人的休闲方式是运动,列出2×2列联表如下:运动 非运动 总计 男性 n5 n 5 25n 女性 n 5 25n 3n 5 总计25n 3n 5n由表中数据,得k =n·n 5·2n 5-n 5·n 522n 5·3n 5·2n 5·3n 5=n 36. 要使调查员在犯错误的概率不超过0.05的前提下认为“休闲方式与性别有关”,则k≥3.841.所以n 36≥3.841.解得n≥138.276.又n5∈N *,所以n≥140.所以被调查的人中,以运动为休闲方式的最少有140×25=56(人).本题属于逆向探求型问题,目的在于训练K 2公式的熟练应用.解题的关键在于根据犯错误概率的上界α确定临界值k 0,然后设出未知数利用K 2≥k 0列出不等式进行解决.这里运用了方程思想和化归思想.有两个分类变量X 与Y ,其一组观测值如下面的2×2列联表所示:y 1 y 2 合计 x 1 a 20-a 20 x 2 15-a 30+a 45 合计155065其中a,15-a 均为大于5的整数,则a 取何值时,在犯错误的概率不超过0.10的前提下认为“X 和Y 有关系”?【解】 查表可知:要使犯错误的概率不超过0.1,则K 2≥2.706, 而K 2=65×[a×30+a -15-a ×20-a ]220×45×15×50=13×65a -300250×45×60=13×13a -60290×60,因为K 2≥2.706, 所以13×13a -60290×60≥2.706.即(13a -60)2≥1 124,所以13a -60≥33.5或13a -60≤-33.5, 解得a≥7.2或a≤2.又⎩⎪⎨⎪⎧a>5,15-a>5, 所以5<a<10,且a ∈Z , 所以a =6,7,8,9,又因为a≥7.2或a≤2,所以a =8或a =9.。
独立性检验的基本思想及其应用【学情分析】:在实际的问题中,经常会面临需要推断的问题,比如研制一种新药,需要推断此药是否有效?有人怀疑吸烟的人更容易患肺癌,那么吸烟是否与患肺癌有关呢?等等。
在对类似的问题作出推断时,我们不能仅凭主观意愿作出结论,需要通过试验来收集数据,并依据独立性检验的原理作出合理的分析推断.在本节的学习中,通过案例分析,使学生学会用假设检验的思想方法解决对于两个分类变量是否有关系的判断问题,并理解统计思维与确定性思维的差异。
【教学目标】:(1)知识与技能:进一步加强阅读三维柱形图和二维条形图的能力;加强理解独立性检验思想,会利用独立性检验方法解决实际问题。
(2)过程与方法:提供多个案例,让学生能自觉运用独立性检验的思维解决问题。
(3)情感态度与价值观:通过提供适当的情境资料,吸引学生的注意力,激发学生的学习兴趣;在合作讨论中学会交流与合作,启迪思维,提高创新能力;通过实际问题的解决和从不同角度对问题的解决,可提高学生应用数学能力。
【教学重点】:理解独立性检验的基本思想及实施步骤,初步应用。
【教学难点】:(1)了解独立性检验的基本思想;(2)了解随机变量2K太大认为两个分类变量是有关系的。
K的含义,2【课前准备】:课件【教学过程设计】:同步练习:(基础题)1、在研究某种新措施对猪白痢的防治效果问题时,得到了以下数据:试问新措施对猪白痢的防治效果如何?[解析]由公式得:()230013236114187.31715015024654k ⨯⨯-⨯=≈⨯⨯⨯,由于7.317>6.635,所以我们有99%的把握认为新措施对猪白痢的防治是有效的。
2、调查某医院某段时间内婴儿出生的时间与性别的关系,得到下面的数据表,试问能以多大的把握认为婴儿的性别与出生时间有关系。
[解析]由公式得:()2892426831 3.689 3.84155343257k ⨯⨯-⨯=≈<⨯⨯⨯,所以没有充分的证据显示婴儿的性别与出生时间有关。
独立性检验和回归直线
——复习课说课稿
一、教材分析和处理
1.本节内容在教材中的地位和作用
本节是高中数学课本选修1-2第三章《统计案例》中的内容,是在学习了用样本估记总体、线性回归等基本知识的基础上,进一步讨论线性回归方法及其应用,并初步了解独立性检验的基本思想,认识统计方法在决策中的作用。
本节内容在近几年的高考试题中是屡见不鲜的,如2011年陕西选9,湖南选4,安徽解20等等,因而是高考中的热点之一。
2.教学目标
知识目标:(1)理解线性回归分析方法及应用;
(2)理解独立性检验的基本思想及应用。
能力目标:(3)培养学生分析问题、解决问题的能力;相互探讨、合作交流、共同提高、团结协作的能力。
3.学情分析
这节课是在学生对回归分析、独立性检验的基本思想有了初步的了解,对课本基础概念有了感性认识的基础上进行巩固加深的。
要想深刻理解,灵活运用,需要进行全面复习。
根据《新课标》的要求,以学生为主体,充分调动学生在课堂上的积极性,运用多媒体,加大直观性和容量,提高学习效率。
二、教法
本课教法以启发式教学法和合作探究法为主,因为在教学中要突出学生的主体地位,培养学生的自主意识和合作意识为根本,整个过程师生互动,学生为主体,教师为主导,共同参与;教师启发、引导、巡查、点拔,充分调动学生的积极性,教学过程采用多媒体展示、多黑板演示,多学生讲解,将教师提供的习题分组完成,重点强化,难点突破,营造活跃的课堂气氛,使课堂成为学生展示的舞台,成功表现自我;各小组成员分工协作,积极动手实践,学习热情高涨,合作探究意识明显增强,打造高效课堂。
三、学法
新课程理念是“以学生的发展为核心”,在学习过程中始终让他们自主学习,成为
学习的主人,将全班学生分成六个小组各自下达学习任务,既明确分工,又互相合作;完成任务,积极演示,全班互动,共同提高。
组内由组长引领,组员互学,互相借鉴,成果共享。
四、教学过程设计
这节课以教师为主导,学生活动为主线,分为导入——展示学习目标——探究学习——反馈练习——学生小结等几个环节。
导入:利用大屏幕,展开“独立性检验与回归直线”的复习课件,教师简要介绍本节在教材中的地位以及在高考中屡次出现,应给予重视,引导学生进入情景展示复习目标;让学生目的明确,集中注意力,快速完成学习任务。
课前演练做到温故而知新,激发求知欲,明确自己的不足。
然后进入知识要点复习阶段,学生对照大屏幕,仔细阅读复习参考书,强化记忆。
典型习题由学生分组完成,各小组选派优秀组员分别演示、讲解,全班群学,教师一一点评,给予鼓励。
然后进行方法提炼,最后学生进行反馈练习。
反馈练习基于现代教学理念下的一种教学策略,以学生为主导,以学生发展为核心,培养学生的解题能力,解题策略。
学生小结说明本节课复习了什么,明白了什么,收获了什么。