必修5 正余弦定理资料整理

知识点串讲必修五第一章：解三角形1．1．1正弦定理1、正弦定理：在一个三角形中，各边和它所对角的正弦的比相等，即sin sin abA B =sin cC =一般地，已知三角形的某些边和角，求其他的边和角的过程叫作解三角形。

2、已知∆ABC 中,∠A 060=，a =求sin sin sin a b c A B C++++ 证明出sin sin a b A B =sin c C ==sin sin sin a b c A B C++++ 解:设sin sin a b A B =(>o)sin c k k C== 则有sin a k A =，sin b k B =，sin c k C = 从而sin sin sin a b c A B C ++++=sin sin sin sin sin sin k A k B k C A B C++++=k又sin a A =2k ==，所以sin sin sin a b c A B C++++=2 评述：在∆ABC 中，等式sin sin a b A B =sin c C ==()0sin sin sin a b c k k A B C ++=>++ 恒成立。

3、已知∆ABC 中,sin :sin :sin 1:2:3A B C =，求::a b c（答案：1:2:3）1.1.2余弦定理1、余弦定理：三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍.即 2222cos a b c bc A =+-2222cos b a c ac B =+-2222cos c a b ab C =+-从余弦定理，又可得到以下推论：222cos 2+-=b c a A bc 222cos 2+-=a c b B ac 222cos 2+-=b a c C ba2、在∆ABC 中，已知=a c 060=B ，求b 及A⑴解：∵2222cos =+-b a c ac B=222+-⋅cos 045=2121)+-=8∴=b求A 可以利用余弦定理，也可以利用正弦定理:⑵解法一：∵cos 2222221,22+-=b c a A bc ∴060.=A解法二：∵sin 0sin sin45,=a A B b2.4 1.43.8,+=21.8 3.6,⨯=∴a ＜c ,即00＜A ＜090,∴060.=A评述：解法二应注意确定A 的取值范围。

必修五第一讲 正弦定理知识梳理1．正弦定理：在一个三角形中，各边和它所对角的正弦的比相等，即a sin A ＝b sin B ＝csin C.2．解三角形：一般地，把三角形的三个角A 、B 、C 和它们的对边a 、b 、c 叫做三角形的元素，已知三角形的几个元素求其他元素的过程叫做解三角形．题型分析[例1] 在△ABC 中，已知a [解] A ＝180°－(B ＋C )＝180°－(60°＋75°)＝45°.由b sin B ＝a sin A 得，b ＝a sin B sin A ＝8×sin 60°sin 45°＝46，由a sin A ＝c sin C得，c ＝a sin C sin A ＝8×sin 75°sin 45°＝8×2＋6422＝4(3＋1)．∴A ＝45°，b ＝46，c ＝4(3＋1)． [变式训练]在△ABC 中，已知c ＝10，A ＝45°，C ＝30°，解这个三角形． 解：∵A ＝45°，C ＝30°，∴B ＝180°－(A ＋C )＝105°.由a sin A ＝c sin C 得a ＝c sin A sin C ＝10×sin 45°sin 30°＝10 2. 由b sin B ＝c sin C 得b ＝c sin B sin C ＝10×sin 105°sin 30°＝20sin 75°，∵sin 75°＝sin (30°＋45°)＝sin 30°cos 45°＋cos 30°sin 45° ＝2＋64，∴b ＝20×2＋64＝52＋5 6.[例2] 在△ABC [解] ∵a sin A ＝c sin C ，∴sin C ＝c sin Aa ＝6×sin 45°2＝32，∴C ＝60°或C ＝120°.当C ＝60°时，B ＝75°，b ＝c sin B sin C ＝6sin 75°sin 60°＝3＋1； 当C ＝120°时，B ＝15°，b ＝c sin B sin C ＝6sin 15°sin 120°＝3－1. ∴b ＝3＋1，B ＝75°，C ＝60°或b ＝3－1，B ＝15°，C ＝120°. [变式训练]在△ABC 中，若c ＝6，C ＝π3，a ＝2，求A ，B ，b .解：由a sin A ＝c sin C ，得sin A ＝a sin C c ＝22.∴A ＝π4或A ＝34π.又∵c ＞a ，∴C ＞A ，∴只能取A ＝π4， ∴B ＝π－π3－π4＝5π12，b ＝c sin Bsin C＝6·sin 5π12sinπ3＝3＋1.[例3] 在△ABC 中，sin 2 A ＝sin 2 B ＋sin 2 C ，且sin A ＝2sin B ·cos C ．试判断△ABC 的形状．[解] 由正弦定理，得sin A ＝a 2R ，sin B ＝b 2R ，sin C ＝c2R.∵sin 2 A ＝sin 2 B ＋sin 2 C ，∴⎝⎛⎭⎫a 2R 2＝⎝⎛⎭⎫b 2R 2＋⎝⎛⎭⎫c 2R 2， 即a 2＝b 2＋c 2，故A ＝90°.∴C ＝90°－B ，cos C ＝sin B .∴2sin B ·cos C ＝2sin 2 B ＝sin A ＝1. ∴sin B ＝22.∴B ＝45°或B ＝135°(A ＋B ＝225°＞180°，故舍去)．∴△ABC 是等腰直角三角形． [变式训练]在△ABC 中，若b ＝a cos C ，试判断该三角形的形状．解：∵b ＝a cos C ，a sin A ＝bsin B＝2R .(2R 为△ABC 外接圆直径)∴sin B ＝sin A ·cos C .∵B ＝π－(A ＋C )，∴sin (A ＋C )＝sin A ·cos C .即sin A cos C ＋cos A sin C ＝sin A ·cos C ， ∴cos A sin C ＝0，∵A 、C ∈(0，π)，∴cos A ＝0，∴A ＝π2，∴△ABC 为直角三角形．[随堂检测]1．(2012·广东高考)在△ABC 中，若∠A ＝60°，∠B ＝45°，BC ＝32，则AC ＝( )A ．43B ．2 3 C. 3D.32解析：选B 由正弦定理得：BC sin A ＝AC sin B ，即32sin 60°＝AC sin 45°，所以AC ＝3232×22＝23，故选B.2．在△ABC 中，a ＝5，b ＝3，C ＝120°，则sin A ∶sin B 的值是( A )A.53B.35C.37D.573．在△ABC 中，若(sin A ＋sin B )(sin A －sin B )＝sin 2 C ，则△ABC 是________三角形． 解析：由已知得sin 2 A －sin 2 B ＝sin 2 C ，根据正弦定理知sin A ＝a 2R ，sin B ＝b 2R ，sin C ＝c2R，所以⎝⎛⎭⎫a 2R 2－⎝⎛⎭⎫b 2R 2＝⎝⎛⎭⎫c 2R 2，即a 2－b 2＝c 2，故b 2＋c 2＝a 2.所以△ABC 是直角三角形．答案：直角 4．(2012·北京高考)在△ABC 中，若a ＝3，b ＝3，∠A ＝π3，则∠C 的大小为________．解析：由正弦定理可知sin B ＝b sin Aa ＝3sin π33＝12，所以∠B ＝π6或5π6(舍去)，所以∠C ＝π－∠A －∠B ＝π－π3－π6＝π2. 5．不解三角形，判断下列三角形解的个数．(1)a ＝5，b ＝4，A ＝120°； (2)a ＝7，b ＝14，A ＝150°； (3)a ＝9，b ＝10，A ＝60°. 解：(1)sin B ＝b sin 120°a ＝45×32＜32，所以△ABC 有一解．(2)sin B ＝b sin 150°a＝1，所以△ABC 无解．(3)sin B ＝b sin 60°a ＝109×32＝539，而32＜539＜1，所以当B 为锐角时，满足sin B ＝539的B 的取值范围为60°＜B ＜90°.当B 为钝角时，有90°＜B ＜120°，也满足A ＋B ＜180°，所以△ABC 有两解．课后作业一、选择题1．在△ABC 中，下列式子与sin A a的值相等的是( )A.b cB.sin B sin AC.sin C cD.csin C解析：选C 由正弦定理得a sin A ＝c sin C ，所以sin A a ＝sin Cc. 2．(2013·浏阳高二检测)在△ABC 中，若sin A >sin B ，则A 与B 的大小关系为( )A ．A >B B ．A <BC ．A ≥BD ．A 、B 的大小关系不确定解析：选A ∵sin A >sin B ，∴2R sin A >2R sin B ，即a >b ，故A >B .3．一个三角形的两个角分别等于120°和45°，若45°角所对的边长是46，那么120°角所对边长是( )A ．4B.12 3 C ．4 3D ．12解析：选D 若设120°角所对的边长为x ，则由正弦定理可得：x sin 120°＝46sin 45°，于是x ＝46·sin 120°sin 45°＝46×3222＝12，故选D.4．△ABC 的三个内角A ，B ，C 所对的边分别为a ，b ，c ，a sin A sin B ＋b cos 2A ＝2a ，则ba＝( )A ．2 3B.2 2C.3D. 2解析：选D 由正弦定理，得sin 2A sin B ＋sin B cos 2A ＝2sin A ，即sin B ·(sin 2A ＋cos 2A )＝2sin A .所以sin B ＝2sin A ．∴b a ＝sin Bsin A＝ 2.5．以下关于正弦定理或其变形的叙述错误的是( )A ．在△ABC 中，a ∶b ∶c ＝sin A ∶sinB ∶sinC B ．在△ABC 中，若sin 2A ＝sin 2B ，则a ＝bC ．在△ABC 中，若sin A ＞sin B ，则A ＞B ，若A ＞B ，则sin A ＞sin B 都成立D ．在△ABC 中，asin A ＝b ＋c sin B ＋sin C解析：选B 由正弦定理易知A ，C ，D 正确．对于B ，由sin 2A ＝sin 2B ，可得A ＝B ，或2A ＋2B ＝π，即A ＝B ，或A ＋B ＝π2，∴a ＝b ，或a 2＋b 2＝c 2，故B 错误.二、填空题6．在△ABC 中，若a ＝14，b ＝76，B ＝60°，则C ＝________.解析：由正弦定理知a sin A ＝b sin B ，又a ＝14，b ＝76，B ＝60°，∴sin A ＝a sin B b ＝14sin 60°76＝22，∵a ＜b ，∴A ＜B ，∴A ＝45°，∴C ＝180°－(B ＋A )＝180°－(60°＋45°)＝75°.答案：75° 7．在△ABC 中，B ＝30°，C ＝120°，则a ∶b ∶c ＝________.解析：A ＝180°－B －C ＝30°，由正弦定理得a ∶b ∶c ＝sin A ∶sin B ∶sin C ，即a ∶b ∶c ＝sin 30°∶sin 30°∶sin 120°＝1∶1∶ 3.答案：1∶1∶ 38．在△ABC 中，若A ＝120°，AB ＝5，BC ＝7，则sin B ＝________.解析：由正弦定理，得sin C ＝AB ·sin A BC ＝5sin 120°7＝5314.可知C 为锐角，∴cos C ＝1－sin 2C ＝1114.∴sin B ＝sin(180°－120°－C )＝sin(60°－C )＝sin 60°·cos C －cos 60°·sin C ＝3314.答案：3314三、解答题9．(2011·安徽高考)在△ABC 中，a ，b ，c 分别为内角A ，B ，C 所对的边长，a ＝3，b ＝2，1＋2cos(B ＋C )＝0，求边BC 上的高．解：由1＋2cos(B ＋C )＝0和B ＋C ＝π－A ，得1－2cos A ＝0，所以cos A ＝12，sin A ＝32.再由正弦定理，得sin B ＝b sin A a ＝22.由b <a 知B <A ，所以B 不是最大角，B <π2，从而cos B ＝1－sin 2B ＝22.由上述结果知sin C ＝sin(A ＋B )＝22×(32＋12)＝6＋24. 设边BC 上的高为h ，则有h ＝b sin C ＝3＋12. 10．在△ABC 中，已知a 2sin B cos B ＝b 2sin Acos A，试数列△ABC 的形状．解：∵a 2sin B cos B ＝b 2sin A cos A ，a ＝2R sin A ，b ＝2R sin B ，∴4R 2sin 2 A sin B cos B ＝4R 2sin 2 B sin Acos A.又∵sin A sin B ≠0，∴sin A cos A ＝sin B cos B ，即sin 2A ＝sin 2B ，∴2A ＝2B ，或2A ＋2B ＝π，即A ＝B ，或A ＋B ＝π2.故△ABC 是等腰三角形或直角三角形．必修五第二讲 余弦定理知识梳理 余弦定理题型分析[例1] 在△ABC 中，若a [解] 由于a ∶b ∶c ＝1∶3∶2，可设a ＝x ，b ＝3x ，c ＝2x .由余弦定理的推论，得cos A ＝b 2＋c 2－a 22bc ＝3x 2＋4x 2－x 22×3x ×2x ＝32，故A ＝30°.同理可求得cos B ＝12，cos C ＝0，所以B ＝60°，C ＝90°.[变式训练]边长为5,7,8的三角形中，最大角与最小角的和是________．解析：设中间角为θ，由于8＞7＞5，故θ的对边的长为7，由余弦定理，得cos θ＝52＋82－722×5×8＝12.所以θ＝60°，故另外两角和为180°－60°＝120°.答案：120°[例2] 在△ABC [解] 由余弦定理得：b 2＝a 2＋c 2－2ac cos B ＝82＋[4(3＋1)]2－2×8×4(3＋1)·cos 60°＝64＋16(4＋23)－64(3＋1)×12＝96，∴b ＝4 6.法一：由cos A ＝b 2＋c 2－a 22bc ＝96＋16(3＋1)2－642×46×4(3＋1)＝22，∵0°＜A ＜180°，∴A ＝45°.故C ＝180°－A －B ＝180°－45°－60°＝75°.法二：由正弦定理a sin A ＝b sin B ，∴8sin A ＝46sin 60°，∴sin A ＝22，∵b ＞a ，c ＞a ，∴a 最小，即A 为锐角．因此A ＝45°.故C ＝180°－A －B ＝180°－45°－60°＝75°. [变式训练]在△ABC ，已知a ＝22，b ＝23，C ＝15°，解此三角形．解：c 2＝a 2＋b 2－2ab cos C ＝(22)2＋(23)2－2×22×23×cos(45°－30°)＝8－43＝(6－2) 2∴c ＝6－ 2. 法一：由余弦定理的推论得cos A ＝b 2＋c 2－a 22bc ＝(23)2＋(6－2)2－(22)22×23×(6－2)＝22.∵0°＜A ＜180°，∴A ＝45°，从而B ＝120°.法二：由正弦定理得sin A ＝a sin C c ＝22×6－246－2＝22.∵a ＜b ，∴A ＜B ，又0°＜A ＜180°，∴A 必为锐角，∴A ＝45°，从而得B ＝120°.[例3] 在△[解] 法一：由余弦定理b 2＝a 2＋c 2－2ac cos B ，得32＝a 2＋(33)2－2a ×33×cos 30∴a 2－9a ＋18＝0，得a ＝3或6.当a ＝3时，A ＝30°，∴C ＝120°.当a ＝6时，由正弦定理得sin A ＝a sin Bb ＝6×123＝1.∴A ＝90°，∴C ＝60°.法二：由b ＜c ，B ＝30°，b ＞c sin 30°＝33×12＝332知本题有两解．由正弦定理得sin C ＝c sin Bb ＝33×123＝32， ∴C ＝60°或120°，当C ＝60°时，A ＝90°，△ABC 为直角三角形．由勾股定理得a ＝b 2＋c 2＝32＋(33)2＝6，当C ＝120°时，A ＝30°，△ABC 为等腰三角形，∴a ＝3.[变式训练]已知：在△ABC 中，cos A ＝35，a ＝4，b ＝3，则c ＝________.解析：A 为b ，c 的夹角，由余弦定理得a 2＝b 2＋c 2－2bc cos A ，∴16＝9＋c 2－6×35c ，整理得5c 2－18c －35＝0.解得c ＝5或c ＝－75(舍)．答案：5[例4] 在△ABC 中，若a cos A [解] 由余弦定理可得a ·b 2＋c 2－a 22bc ＋b ·a 2＋c 2－b 22ac ＝c ·a 2＋b 2－c 22ab等式两边同乘以2abc 得a 2(b 2＋c 2－a 2)＋b 2(a 2＋c 2－b 2)＝c 2(a 2＋b 2－c 2)，整理化简得a 4＋b 4－2a 2b 2＝c 4，∴(a 2－b 2)2＝c 4.因此有a 2－b 2＝c 2或b 2－a 2＝c 2.即a 2＝b 2＋c 2或b 2＝a 2＋c 2故△ABC 为直角三角形． [变式训练]．在△ABC 中，若cos A ＝sin Bsin C，试判断其形状．解：由cos A ＝sin B sin C 得cos A ＝bc ，即b 2＋c 2－a 22bc ＝b c，∴b 2＋c 2－a 2＝2b 2，即a 2＋b 2＝c 2，因此△ABC 是以C 为直角的直角三角形．[例5]如图所示，在四边形ABCD 中，AD ⊥CD ，AD ＝10，AB ＝14，∠BDA ＝60°，∠BCD ＝135°，求出BC 的长． [解]设BD ＝x .在△ABD 中，根据余弦定理，AB 2＝AD 2＋BD 2－2AD ·BD cos ∠BDA ，∴142＝102＋x 2－2×10×x cos60°，即x 2－10x －96＝0，解得x 1＝16，x 2＝－6(舍去)，∴BD ＝16.∵AD ⊥CD ，∠BDA ＝60°，∴∠CDB ＝30°.在△BCD 中，由正弦定理，BC sin ∠CDB ＝BDsin ∠BCD，∴BC ＝16sin 30°sin 135°＝8 2.注：将四边形ABCD 分解为两个△ABD 和△BCD ，利用余弦定理列出关于x 的一元二次方程，化简方程时易出错，应注意步骤及计算的准确性． 由AD ⊥CD ，∠BDA ＝60°得∠CDB ＝30°，学生有时不易想到． [变式训练]如图所示，在△ABC 中，已知B ＝45°，D 是BC 边上一点，AD ＝5，AC ＝7，DC ＝3，求AB . 解：在△ADC 中，cos C ＝AC 2＋DC 2－AD 22·AC ·DC ＝72＋32－522×7×3＝1114.又∵0°＜C ＜180°，∴sin C ＝5314.在△ABC 中，AC sin B ＝AB sin C ，∴AB ＝sin C sin B ·AC ＝5314·2·7＝562. [随堂注册]1．在△ABC 中，已知A ＝30°，且3a ＝3b ＝12，则c 的值为( C )A ．4B ．8C ．4或8D ．无解2．在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，若c 2－a 2－b 22ab＞0，则△ABC ( C )A ．一定是锐角三角形 B.一定是直角三角形 C ．一定是钝角三角形 D ．是锐角或直角三角形3．(2012·陕西高考)在△ABC 中，角A ，B ，C 所对边的长分别为a ，b ，c .若a ＝2，B ＝π6，c ＝23，则b ＝________.解析：由余弦定理得b 2＝a 2＋c 2－2ac cos B ＝4＋12－2×2×23×32＝4，所以b ＝2.答案：2 4．在△ABC 中，已知a ＝7，b ＝3，c ＝5，则最大的角是________．解析：∵a ＞c ＞b ，∴A 为最大角．cos A ＝b 2＋c 2－a 22bc ＝32＋52－722×3×5＝－12，又∵0°＜A ＜180°，∴A ＝120°.答案：120°5．在△ABC 中，已知a ＝5，b ＝3，角C 的余弦值是方程5x 2＋7x －6＝0的根，求第三边c 的长．解：5x 2＋7x －6＝0可化为(5x －3)(x ＋2)＝0.∴x 1＝35，x 2＝－2(舍去)．∴cos C ＝35.根据余弦定理，c 2＝a 2＋b 2－2ab cos C ＝52＋32－2×5×3×35＝16∴c ＝4，即第三边长为4.课后作业一、选择题1．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若A ＝π3，a ＝3，b ＝1，则c ＝( B )A ．1B.2C.3－1D. 32．在△ABC 中，若a ＝8，b ＝7，cos C ＝1314，则最大角的余弦值是( )A ．－15B.－16 C ．－17 D ．－18解析：选C 由余弦定理，得c 2＝a 2＋b 2－2ab cos C ＝82＋72－2×8×7×1314＝9，所以c ＝3，故a 最大，所以最大角的余弦值为cos A ＝b 2＋c 2－a 22bc ＝72＋32－822×7×3＝－17.3．在△ABC 中，B ＝60°，b 2＝ac ，则此三角形一定是( B )A ．直角三角形 B.等边三角形 C ．等腰直角三角形 D ．钝角三角形4．(2013·宁阳高二检测)在△ABC 中，b cos A ＝a cos B ，则△ABC 是( )A ．等边三角形B.等腰三角形 C ．直角三角形 D ．锐角三角形解析：选B 因为b cos A ＝a cos B ，所以b ·b 2＋c 2－a 22bc ＝a ·a 2＋c 2－b 22ac.所以b 2＋c 2－a 2＝a 2＋c 2－b 2.所以a 2＝b 2.所以a ＝b .故此三角形是等腰三角形．5．在△ABC 中，B ＝60°，最大边与最小边之比为(3＋1)∶2，则最大角为( )A ．45°B.60° C ．75° D ．90°解析：选C 由题意可知c ＜b ＜a ，或a ＜b ＜c ，不妨设c ＝2x ，则a ＝(3＋1)x ，∴cos B ＝a 2＋c 2－b 22ac.即12＝(3＋1)2x 2＋4x 2－b 22·(3＋1)x ·2x ∴b 2＝6x 2.∴cos C ＝a 2＋b 2－c 22ab ＝(3＋1)2x 2＋6x 2－4x 22(3＋1)x ·6x＝22，∴C ＝45°， ∴A ＝180°－60°－45°＝75°. 二、填空题6．(2012·湖北高考)设△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c .若(a ＋b －c )(a ＋b ＋c )＝ab ，则角C ＝________解析：∵(a ＋b )2－c 2＝ab ，∴cos C ＝a 2＋b 2－c 22ab ＝－12，C ＝2π3.答案：2π37．在△ABC 中，A ＝120°，AB ＝5，BC ＝7，则sin Bsin C的值为________．解析：由余弦定理可得49＝AC 2＋25－2×5×AC ×cos 120°，整理得：AC 2＋5·AC －24＝0，解得AC ＝3或AC ＝－8(舍去)，再由正弦定理可得sin B sin C ＝AC AB ＝35.答案：358．在△ABC 中，若sin A ∶sin B ∶sin C ＝3∶5∶7，则C 的大小是________．解析：因为sin A ∶sin B ∶sin C ＝3∶5∶7，由正弦定理可得a ∶b ∶c ＝3∶5∶7，设a ＝3k (k ＞0)，则b ＝5k ，c ＝7k ，由余弦定理的推论得cos C ＝a 2＋b 2－c 22ab ＝－12，又0°＜C ＜180°，所以C ＝120°.答案：120°三、解答题9．在△ABC 中，若已知(a ＋b ＋c )(a ＋b －c )＝3ab ，并且sin C ＝2sin B cos A ，试判断△ABC 的形状． 解：由正弦定理，可得sin B ＝b 2R ，sin C ＝c2R .由余弦定理，得cos A ＝b 2＋c 2－a 22bc.代入sin C ＝2sin B cos A ，得c ＝2b ·b 2＋c 2－a 22bc .整理得 a ＝b .又因为(a ＋b ＋c )(a ＋b －c )＝3ab ，所以a 2＋b 2－c 2＝ab ，即cos C ＝a 2＋b 2－c 22ab ＝12.故C ＝π3.又a ＝b ，所以△ABC 为等边三角形．10．在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，且2b ·cos A ＝c ·cos A ＋a ·cos C(1)求角A 的大小；(2)若a ＝7，b ＋c ＝4，求bc 的值．解：(1)根据正弦定理2b ·cos A ＝c ·cos A ＋a ·cos C ⇒2cos A sin B ＝sin A cos C ＋cos A sin C ＝sin (A ＋C )＝sin B ，∵sin B ≠0，∴cos A ＝12，∵0°＜A ＜180°，∴A ＝60°.(2)由余弦定理得：7＝a 2＝b 2＋c 2－2bc ·cos 60°＝b 2＋c 2－bc ＝(b ＋c )2－3bc ，把 b ＋c ＝4代入得bc ＝3，故bc ＝3.必修五第三讲 正、余弦定理在三角形中的应用知识梳理三角形的面积公式(1)S ＝12a ·h a (h a 表示a 边上的高)．(2)S ＝12ab sin C ＝12bc sin A ＝12ac sin B .三角形的面积公式S ＝12ab sin C 与原来的面积公式S ＝12a ·h (h 为a 边上的高)的关系为：h ＝b sin C ，实质上b sin C 就是△ABC 中a 边上的高．题型分析[例1] 在△ABC 中，已知C ＝[解] 由正弦定理知AB sin C ＝AC sin B ，即23sin 120°＝2sin B ，所以sin B ＝12，由于AB ＞AC ，所以C ＞B ，故B ＝30°.从而A ＝180°－120°－30°＝30°.所以△ABC 的面积S ＝12AB ·AC ·sin A ＝12·23·2·sin 30°＝ 3.[变式训练]．(1)在△ABC 中，若A ＝60°，b ＝16，S △ABC ＝643，则c ＝________.(2)在△ABC 中，若a ＝3，b ＝2，c ＝4，则其面积等于________．解析：(1)由已知得S △ABC ＝12·bc ·sin A ，即643＝12×16×c ×sin 60°，解得c ＝16.(2)由余弦定理得cos A ＝b 2＋c 2－a 22bc ＝4＋16－92×2×4＝1116，所以sin A ＝1－cos 2 A ＝31516，于是S △ABC ＝12bc sin A ＝12×2×4×31516＝3154.答案：(1)16 (2)3154[例2] 在△ABC 中，求证：a －c cos B b －c cos A ＝sin Bsin A.[解] 法一：左边＝a －c (a 2＋c 2－b 2)2ac b －c (b 2＋c 2－a 2)2bc ＝a 2－c 2＋b 22a ·2b b 2－c 2＋a 2＝b a ＝2R sin B 2R sin A ＝sin Bsin A＝右边，其中R 为△ABC 外接圆的半径．∴a －c cos B b －c cos A ＝sin Bsin A.法二：左边＝sin A －sin C cos B sin B －sin C cos A ＝sin (B ＋C )－sin C ·cos B sin (A ＋C )－sin C ·cos A ＝sin B cos C sin A cos C ＝sin Bsin A＝右边，(cos C ≠0)∴a －c ·cos Bb －c ·cos A ＝sin B sin A.[变式训练]．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，求证：a b －ba ＝c ⎝⎛⎭⎫cos B b－cos A a .证明：由余弦定理的推论得cos B ＝a 2＋c 2－b 22ac ，cos A ＝b 2＋c 2－a 22bc，代入等式右边，得右边＝c ⎝⎛⎭⎫a 2＋c 2－b 22abc－b 2＋c 2－a 22abc ＝2a 2－2b 22ab ＝a 2－b 2ab ＝a b －b a ＝左边，∴a b －ba ＝c ⎝⎛⎭⎫cos Bb －cos A a .[例3] (2012·江西高考)在△B －C )－1＝6cos B cos C .(1)求cos A ； (2)若a ＝3，△ABC 的面积为22，求b ，c .[解] (1)由3cos(B －C )－1＝6cos B cos C ，得3(cos B cos C －sin B sin C )＝－1，即cos(B ＋C )＝－13，从而cos A ＝－cos(B ＋C )＝13.(2)由于0<A <π，cos A ＝13，所以sin A ＝223.又S △ABC ＝22，即12bc sin A ＝22，解得bc ＝6.由余弦定理a 2＝b 2＋c 2－2bc cos A ，得b 2＋c 2＝13，解方程组⎩⎪⎨⎪⎧ bc ＝6，b 2＋c 2＝13，得⎩⎪⎨⎪⎧ b ＝2，c ＝3，或⎩⎪⎨⎪⎧b ＝3，c ＝2.解决三角形的综合问题，除灵活运用正、余弦定理及三角形的有关知识外，一般还要用到三角函数、三角恒等变换、方程等知识．因此，掌握正、余弦定理，三角函数的公式和性质是解题关键．[变式训练]．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且满足cos A 2＝255，AB ·AC ＝3.(1)求△ABC 的面积； (2)若b ＋c ＝6，求a 的值．解：(1)∵cos A 2＝255，∴cos A ＝2cos 2A 2－1＝35，sin A ＝45.又由AB ·AC ＝3，得bc cos A ＝3，∴bc ＝5，∴S △ABC ＝12bc sin A ＝2.(2)∵bc ＝5，b ＋c ＝6，∴b ＝5，c ＝1或b ＝1，c ＝5.由余弦定理，得a 2＝b 2＋c 2－2bc cos A ＝20， ∴a ＝2 5.[例4]如图，在四边形ABCD 中，AC ＝CD ＝12AB ＝1，AB ·AC ＝1，sin ∠BCD ＝35.(1)求BC 边的长；(2)求四边形ABCD 的面积．[解] (1)∵AC ＝CD ＝12AB ＝1，∴AB ·AC ＝AB ·AC ·cos ∠BAC ＝2cos ∠BAC ＝1，∴cos ∠BAC ＝12，∴∠BAC ＝60°.(3分)在△ABC 中，由余弦定理有：BC 2＝AB 2＋AC 2－2AB ·AC ·cos ∠BAC ＝22＋12－2×2×1×12＝3，∴BC ＝3(6分)(2)由(1)知，在△ABC 中有：AB 2＝BC 2＋AC 2，∴△ABC 为直角三角形，且∠ACB ＝90°，(7分) ∴S △ABC ＝12BC ·AC ＝12×3×1＝32.(8分)又∠BCD ＝∠ACB ＋∠ACD ＝90°＋∠ACD ，sin ∠BCD ＝35，∴cos ∠ACD ＝35，(9分)从而sin ∠ACD ＝1－cos 2∠ACD ＝45，(10分)∴S △ACD ＝12AC ·CD ·sin ∠ACD ＝12×1×1×45＝25.(11分)∴S 四边形ABCD ＝S △ABC ＋S △ACD ＝32＋25＝4＋5310.(12分)[变式训练]在△ABC ，中，AB ＝2，cos C ＝277，D 是AC 上一点，AD ＝2DC ，且cos ∠DBC ＝5714. 求：(1)∠BDA 的大小；(2) AD ·CB .解：(1)由已知得cos ∠DBC ＝5714，cos C ＝277，从而sin ∠DBC ＝2114，sin C ＝217，∴cos ∠BDA ＝cos(∠DBC ＋∠C )＝5714×277－2114×217＝12，∴∠BDA ＝π3.(2)设DC ＝x ，则AD ＝2x ，AC ＝3x ，设BC ＝a ，则在△DBC 中，由正弦定理得x sin ∠DBC ＝asin ∠BDC ，∴a ＝7x .在△ABC 中，由余弦定理，得4＝(3x )2＋(7x )2－2·3x ·7x ·277.解得x ＝1，∴AC ＝3，BC ＝7.∴AD ·CB ＝AD ·CB cos(π－C )＝2×7×⎝⎛⎭⎫－277＝－4. [随堂检测]1．已知△ABC 的面积为32，且b ＝2，c ＝3，则A 的大小为( )A ．60°或120°B ．60°C ．120°D ．30°或150°解析：选A 由S △ABC ＝12bc sin A 得32＝12×2×3×sin A ，所以sin A ＝32，故A ＝60°或120°，故选A.2．在△ABC 中，若AC AB ＝cos Bcos C，则( )A ．A ＝CB.A ＝B C ．B ＝CD ．以上都不正确解析：C ∵AC AB ＝sin B sin C ＝cos Bcos C ∴sin B cos C ＝cos B sin C ∴sin(B －C )＝0又∵－π＜B －C ＜π，∴B －C ＝0，即B ＝C .3．等腰△ABC 中，顶角A ＝120°，腰长AB ＝1，则底边BC 长为________． 解析：易知∠B ＝∠C ＝30°，由正弦定理知：BC sin 120°＝1sin 30°，∴BC ＝ 3.答案： 34．三角形的两边分别为3 cm,5 cm ，它们所夹角的余弦值为方程5x 2－7x －6＝0的根，则这个三角形的面积为________．解析：方程5x 2－7x －6＝0的两根为x 1＝2，x 2＝－35，因此两边夹角的余弦值等于－35，并可求得正弦值为45，于是三角形面积S ＝12×3×5×45＝6(cm 2)．答案：6 cm 25．在△ABC 中，若B ＝30°，AB ＝23，AC ＝2，求△ABC 的面积．解：∵AB ＝23，AC ＝2，B ＝30°，∴根据正弦定理，有sin C ＝AB sin B AC ＝23×122＝32，又∵AB ＞AC ，∴C ＞B ，则C 有两解，(1)当C 为锐角时，C ＝60°，A ＝90°，∴S △ABC ＝12AB ·AC sin A ＝2 3.(2)当C 为钝角时，C ＝120°，A ＝30°，∴S △ABC ＝12AB ·AC sin A ＝ 3.综上可知，△ABC 的面积为23或 3.课后作业一、选择题1．在△ABC 中，已知AB ＝2，BC ＝5，△ABC 的面积为4，若∠ABC ＝θ，则cos θ是( )A.35B.－35 C ．±35 D ．±45解析：选C ∵S △ABC ＝12AB ·BC sin ∠ABC ＝12×2×5×sin θ＝4.∴sin θ＝45.又θ∈(0，π)，∴cos θ＝±1－sin 2 θ＝±35.2．在△ABC 中，已知A ＝30°，a ＝8，b ＝83，则△ABC 的面积为( )A ．32 3 B.16 C ．323或16 D ．323或16 3解析：选D 在△ABC 中，由正弦定理a sin A ＝b sin B ，得sin B ＝b sin A a ＝83×128＝32，又b ＞a ，∴B ＝60°或120°.当B ＝60°时，C ＝180°－30°－60°＝90°，∴S △ABC ＝12×8×83＝323；当B ＝120°时，C ＝180°－30°－120°＝30°，∴S △ABC ＝12ab sin C ＝12×8×83×12＝16 3.3．在△ABC 中，A ＝60°，AB ＝2，且△ABC 的面积S △ABC ＝32，则边BC 的边长为( ) A. 3B.3C.7 D ．7解析：选A ∵S △ABC ＝12AB ·AC sin A ＝32，∴AC ＝1由余弦定理可得BC 2＝AB 2＋AC 2－2AB ·AC cos A＝4＋1－2×2×1×cos 60°＝3.即BC ＝ 3.4．△ABC 的周长为20，面积为103，A ＝60°，则BC 的边长等于( )A ．5B.6 C ．7D ．8解析：选C 如图由题意得⎩⎪⎨⎪⎧a ＋b ＋c ＝20 (1)12bc sin 60°＝10 3 (2)a 2＝b 2＋c 2－2bc cos 60° (3)由(2)得bc ＝40.由(3)得a 2＝b 2＋c 2－bc ＝(b ＋c )2－3bc ＝(20－a )2－3×40∴a ＝7.5．某人从出发点A 向正东走x m 后到B ，向左转150°再向前走3 m 到C ，测得△ABC 的面积为334 m 2，则此人这时离开出发点的距离为( )A ．3 m B. 2 m C ．2 3 m D. 3 m解析：选D 在△ABC 中，S ＝12AB ×BC sin B ，∴334＝12×x ×3×sin 30°，∴x ＝ 3.由余弦定理，得AC ＝ AB 2＋BC 2－2AB ×BC ×cos B ＝3＋9－9＝ 3 (m)．二、填空题6．△ABC 的两边长分别为2,3，其夹角的余弦值为13，则其外接圆的半径为________．解析：不妨设b ＝2，c ＝2，cos A ＝13，则a 2＝b 2＋c 2－2bc ·cos A ＝9，∴a ＝3.又∵sin A ＝1－cos 2 A ＝223，∴外接圆半径为R ＝a 2sin A ＝32·223＝928.答案：9287．一艘船以4 km /h 的速度沿着与水流方向成120°的方向航行，已知河水流速为2 km/h ，则经过 3 h ，该船实际航程为________．解析：如图所示，在△ACD 中，AC ＝23，CD ＝43，∠ACD ＝60°，∴AD 2＝12＋48－2×23×43×12＝36，∴AD ＝6，即该船实际航程为6 km.答案：6 km8．在△ABC 中，a ＝b ＋2，b ＝c ＋2，又知最大角的正弦等于32，则三边长为________．解析：由题意知a 边最大．sin A ＝32，∴A ＝120°，∴a 2＝b 2＋c 2－2bc cos A .∴a 2＝(a －2)2＋(a －4)2＋(a －2)(a －4)．∴a 2－9a ＋14＝0，a ＝2(舍去)，a ＝7.∴b ＝a －2＝5，c ＝b －2＝3.答案：a ＝7，b ＝5，c ＝3 三、解答题9．在△ABC 中，若c ＝4，b ＝7，BC 边上的中线AD 的长为72，求边长a .解：∵AD 是BC 边上的中线，∴可设CD ＝DB ＝x ，则CB ＝a ＝2x .∵c ＝4，b ＝7，AD ＝72，在△ACD 中，有cos C ＝72＋x 2－(72)22×7×x ，在△ABC 中，有cos C ＝72＋(2x )2－422×7×2x .∴49＋x 2－49414x ＝49＋4x 2－1628x 解得x＝92.∴a ＝2x ＝9. 10．(2010·浙江高考)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，设S 为△ABC 的面积，满足S ＝34(a 2＋b 2－c 2)．(1)求角C 的大小；(2)求sin A ＋sin B 的最大值．解：(1)由题意可知12ab sin C ＝34·2ab cos C ，所以tan C ＝3，因为0＜C ＜π，所以C ＝π3.(2)由已知sin A ＋sin B ＝sin A ＋sin(π－C －A )＝sin A ＋sin(2π3－A )＝sin A ＋32cos A ＋12sin A ＝3sin(A ＋π6)≤ 3.当△ABC 为正三角形时取等号，所以sin A ＋sin B 的最大值是 3.。

正余弦定理是三角学中的重要知识点，用于解决与三角形相关的问题。

下面是对正余弦定理的知识点及题型归纳：一、正弦定理1. 定义：在任意三角形ABC中，设角A、B、C所对应的边分别为a、b、c，那么有sinA/a = sinB/b = sinC/c。

2. 性质：-等式两边同时乘以任意非零常数，等式仍然成立；-等式两边同时除以相同的角，等式仍然成立；-等式两边同时取反函数，等式仍然成立。

3. 应用：-已知三个角的度数，求边长；-已知两个边的长度，求第三个边的长度；-已知一个角和一条边的长度，求另外两个角的度数；-已知一个角和两条边的长度，求第三个角的度数。

二、余弦定理1. 定义：在任意三角形ABC中，设角A、B、C所对应的边分别为a、b、c，那么有cosA = (b ²+ c²- a²) / (2bc)。

2. 性质：-等式两边同时乘以任意非零常数，等式仍然成立；-等式两边同时除以相同的角，等式仍然成立；-等式两边同时取反函数，等式仍然成立。

3. 应用：-已知三个角的度数，求边长；-已知两个边的长度，求第三个边的长度；-已知一个角和一条边的长度，求另外两个角的度数；-已知一个角和两条边的长度，求第三个角的度数。

三、题型归纳1. 已知三个角的度数，求边长：-根据正弦定理或余弦定理，将已知的角度代入公式中，求解边长；-如果已知的是弧度制的角度，需要将其转换为角度制。

2. 已知两个边的长度，求第三个边的长度：-根据正弦定理或余弦定理，将已知的两个边的长度代入公式中，求解第三个边的长度；-如果已知的是弧度制的角度，需要将其转换为角度制。

3. 已知一个角和一条边的长度，求另外两个角的度数：-根据正弦定理或余弦定理，将已知的角度和边的长度代入公式中，求解另外两个角的度数；-如果已知的是弧度制的角度，需要将其转换为角度制。

4. 已知一个角和两条边的长度，求第三个角的度数：-根据正弦定理或余弦定理，将已知的角度和两条边的长度代入公式中，求解第三个角的度数；-如果已知的是弧度制的角度，需要将其转换为角度制。

高中数学必修五公式声明：本文非原创，由于界面阅读感不好而本人进行重新排版。

第一章 三角函数一．正弦定理：2(sin sin sin a b cR R A B C===为三角形外接圆半径） 变形：2sin (sin )22sin (sin )22sin (sin )2a a R A A R b b R B B R c c R C C R ⎧==⎪⎪⎪==⎨⎪⎪==⎪⎩推论：::sin :sin :sin a b c A B C =二．余弦定理：三．三角形面积公式：111sin sin sin ,222ABC S bc A ac B ab C ∆===第二章 数列一．等差数列： 1.定义：a n+1-a n =d (常数)2.通项公式：()d n a a n ∙-+=11或()d m n a a m n ∙-+=3.求和公式:()()d n n n n a a a S n n 21211-+=+=4.重要性质(1)a a a a q p n m q p n m +=+⇒+=+(2) m,2m,32m m m S S S S S --仍成等差数列二．等比数列：1.定义：)0(1≠=+q q a a nn 2.通项公式：q a a n n 11-∙=或q a a mn m n -∙=3.求和公式: ）（1q ,1==na S n ）（1q 11)1(11≠--=--=qqa a q q a S n n n2222222222cos 2cos 2cos a b c bc Ab ac ac B c a b ab C =+-=+-=+-222222222cos 2cos 2cos 2b c a A bca cb B aca b c C ab+-=+-=+-=4.重要性质（1）a a a a q p n m q p n m =⇒+=+(2)()m,2m,32q 1m m m m S S S S S --≠-仍成等比数列或为奇数三．数列求和方法总结：1.等差等比数列求和可采用求和公式(公式法).2.非等差等比数列可考虑(分组求和法) ,(错位相减法)等转化为等差或等比数列再求和, 若不能转化为等差或等比数列则采用(拆项相消法)求和.注意(1):若数列的通项可分成两项之和（或三项之和）则可用（分组求和法）。

必修五：正弦定理和余弦定理一：正弦定理1：定理内容：在一个三角形中，各边的长和它所对角的正弦的比相等，即R Cc B b A a 2sin sin sin ===（R 是三角形外接圆半径） 2：公式变形（1）R Aa C B A cb a 2sin sin sin sin ==++++ （2）⎪⎩⎪⎨⎧C R c B R b A R a sin 2sin 2sin 2===或R c C R b B R a A 2sin ,2sin ,2sin === （3）⎪⎩⎪⎨⎧B c C b A c C a A b B a sin sin sin sin sin sin ===（4）Rabc A bc B ac C ab S ABC 4sin 21sin 21sin 21====∆ 以下是ABC ∆内的边角关系：熟记（5）B A B A b a >⇔>⇔>sin sin （大边对大角）（6）B A B A cos cos <⇔>（7）⎪⎩⎪⎨⎧+=+=+=)sin(sin )sin(sin )sin(sin B A C C A B C B A 思考A cos 与)cos(C B +的关系（8）2cos 2sin C B A += （9）若AD 是ABC ∆的角平分线，则AC DC AB DB = 思考题：1：若B A sin sin =，则B A ,有什么关系？2：若B A 2sin 2sin =，则B A ,有什么关系？3：若B A cos cos =，则B A ,有什么关系？4：若21sin >A ，则角A 的范围是什么？解三角形：已知三角形的几个元素，求其他元素的过程叫做解三角形.例1：已知ABC ∆，根据下列条件，解三角形.（1）10,45,60=︒=∠︒=∠a B A .（2）︒=∠==120,4,3A b a .（3）︒=∠==30,4,6A b a .（4）︒=∠==30,16,8A b a .（5）︒=∠==30,4,3A b a .思考：在已知“边边角”的情况下，如何判断三角形多解的情况判断方法:（1）用正弦定理：比较正弦值与1的关系（2）作图法：用已知角所对的高与已知角所对的边长比较.练习：（1）若︒=∠==45,12,6A b a ，则符合条件的ABC ∆有几个？（2）若︒=∠==30,12,6A b a ，则符合条件的ABC ∆有几个？（3）若︒=∠==45,12,9A b a ，则符合条件的ABC ∆有几个？例2：根据下列条件，判断三角形形状.（1）C B A 222sin sin sin =+.（2）C B A cos sin 2sin =（3）B b A a cos cos =（4）A b B a tan tan 22=二：余弦定理1：定理内容：三角形任何一边的平方等于其他两边的平方和减去这两边与它们夹角的余弦的积的两倍.即A bc c b a cos 2222-+=B ac c a b cos 2222-+=C ab b a c cos 2222-+= 另一种形式：bca cb A 2cos 222-+=. 请写出另两个：例1：根据下列条件，解三角形.（1）在ABC ∆中，︒=∠==120,4,5C b a ，求边c .（2）在ABC ∆中，︒=∠==60,8,5C b a ，求边c .（3）在ABC ∆中，8,7,5===c b a ，求最大角与最小角的和.（4）在ABC ∆中，13:8:7sin :sin :sin =C B A ，求C cos .（5）在ABC ∆中，8,120,34=+︒=∠=b a C c ，求ABC ∆的面积.（6）在ABC ∆中，34,60,4=︒=∠=∆ABC S C c ，求ABC ∆的周长.（7）在ABC ∆中，1)(22=--bcc b a ，求A ∠. （8）在ABC ∆中，4,3,2===c b a ，判断ABC ∆的形状.（9）求证：在ABC ∆中，)cos cos cos (2222C ab B ac A bc c b a ++=++.（10）求证：平行四边形两对角线的平方和等于它各边的平方和.。

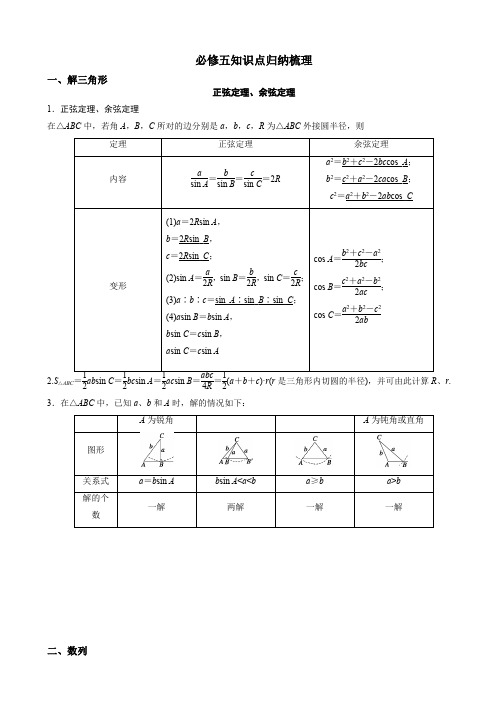
必修五知识点归纳梳理一、解三角形正弦定理、余弦定理1．正弦定理、余弦定理在△ABC中，若角A，B，C所对的边分别是a，b，c，R为△ABC外接圆半径，则2.S△ABC＝12ab sin C＝12bc sin A＝12ac sin B＝abc4R＝12(a＋b＋c)·r(r是三角形内切圆的半径)，并可由此计算R、r.3．在△ABC中，已知a、b和A时，解的情况如下：a＝b sin A b sin A<a<b a≥b a>b 二、数列1．数列的定义按照一定顺序排列的一列数称为数列，数列中的每一个数叫做这个数列的项． 2．数列的分类3.数列的表示法数列有三种表示法，它们分别是列表法、图象法和解析法． 4．数列的通项公式如果数列{a n }的第n 项与序号n 之间的关系可以用一个式子来表示，那么这个公式叫做这个数列的通项公式．5.数列通项求法一、观察法观察法是求数列通项公式的最基本的方法，其实质就是通过观察数列的特征，找出各项共同的构成规律，横向看各项之间的关系结构，纵向看各项与项数之间的关系，从而确定出数列的通项二、公式法求通项直接利用等差数列或等比数列的定义求通项的方法叫定义法，这种方法适应于已知数列类型的题目．d n a a n ）（11-+= （已知数列{a n }为等差数列） 11-*=n n b b q（已知数列{b n }为等比数列）三、由数列的前n 项和求数列通项（应用与的关系求通项）有些数列给出{}的前n 项和与的关系式=，利用该式写出，两式做差，再利用导出与的递推式，从而求出。

利用公式求解时，要注意对n 分类讨论，但若能合写时一定要合并．四、由数列的递推关系求通项公式对于递推公式确定的数列的求解，通常可以通过递推公式的变换，转化为等差数列或等比数列问题，有时也用到一些特殊的转化方法与特殊数列. 类型1：递推公式为nS na n a n S n a n S ()n f a 11()n n S f a ++=11n n n a S S ++=-1n a +n a n a ⎩⎨⎧≥⋅⋅⋅⋅⋅⋅⋅-=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=-211n S S n S a n nn n )(1n f a a n n +=+解法：把原递推公式转化为，利用累加法(逐差相加法)求解。

1.1 正弦定理和余弦定理一、正弦定理：在一个三角形中，各边和它所对角．．．．．．．的正弦的比相等，即：A a sin ＝B b sin ＝C csin 注意：（1）正弦定理中，各边与其对角的正弦严格对应；（2）正弦定理中的比值是一个定值，具有一定几何意义，即为三角形外接圆的直径：A a sin ＝B b sin ＝Ccsin ＝2R [ R 指的是三角形外接圆半径 ]；（3）正弦定理主要实现三角形中的边角互化．．．．．．．．．．．．．．．．．；（4）S ＝C ab sin 21＝A bc sin 21＝B ac sin 21；（5）常用的公式： ①A ＋B ＋C ＝π，sin(A ．．．．．＋．B)．．＝．sinC ．．．．，． cos(A ．．．．．＋．B)．．＝－．．cosC ．．．．，．tan(A ．．．．．＋．B)．．＝－．．tanC ．．．．，．sin 2B A +＝cos 2C ，cos 2B A +＝sin 2C；②a ＝2RsinA ，b ＝2RsinB ，c ＝2RsinC ；③A ＞B ⇔a ＞b 【大角对大边】；④a ＋b ＞c ，a －b ＜c ；⑤a ：b ：c ＝sinA ：sinB ：sinC ；⑥a sinB ＝bsinA ，bsinC ＝csinB ，a sinC ＝csinA 。

例1：下列有关正弦定理的叙述：（1）正弦定理只适用于锐角三角形；（2）正弦定理不适用于直角三角形；（3）在某一确定的三角形中，各边与它所对角的正弦的比是一定值；（4）在△ABC 中，sinA ：sinB ：sinC ＝ a ：b ：c 。

其中正确的个数有（ ） A ：1个 B ：2个 C ：3个 D ：4个 【解析】：B变式练习1：在△ABC 中，角A ：角B ：角C ＝2 ：1 ：1，则a ：b ：c 等于（ ）A ：4 ：1 ：1B ：2 ：1 ：1C ：2 ：1 ：1D ：3 ：1 ：1 【解析】：C变式练习2：在△ABC 中，角A ：角B ：角C ＝4 ：1 ：1，则a ：b ：c 等于（ ）A ：4 ：1 ：1B ：2 ：1 ：1C ：2 ：1 ：1D ：3 ：1 ：1 【解析】：D例2：在△ABC 中，a ＝2，b ＝1，∠A ＝450，∠B ＝___________。

高中数学知识点总结正弦定理与余弦定理正弦定理与余弦定理是高中数学中的重要知识点，用于求解不规则三角形的边长和角度。

本文将对这两个定理进行详细总结与讲解。

一、正弦定理1.1 定义正弦定理是指在任意三角形中，三条边与其对应的角的正弦值之间的关系。

设三角形的三边分别为a、b、c，对应的角度为A、B、C，则正弦定理的表达式为：a/sinA = b/sinB = c/sinC1.2 推导我们通过利用三角形的面积公式S=1/2 * a * b * sinC，并将其转换为对角线的形式，可以得到正弦定理的推导过程。

1.3 应用正弦定理可以用于求解不规则三角形的边长和角度。

当我们已知三条边或者两条边和夹角时，可以利用正弦定理求解未知的边长或者角度。

二、余弦定理2.1 定义余弦定理是指在任意三角形中，三条边和它们对应的角之间的关系。

设三角形的三边分别为a、b、c，对应的角度为A、B、C，则余弦定理的表达式为：c^2 = a^2 + b^2 - 2ab * cosC2.2 推导我们可以通过利用向量的几何关系，将余弦定理的表达式推导出来。

这个过程较为繁琐，这里就不做详细讲解。

2.3 应用余弦定理可以用于求解不规则三角形的边长和角度。

当我们已知三条边或者两条边和夹角时，可以利用余弦定理求解未知的边长或者角度。

三、正弦定理与余弦定理的比较3.1 适用范围正弦定理适用于任意三角形，而余弦定理只适用于任意三角形，不能用于直角三角形。

3.2 计算难度正弦定理的计算相对简单，只需要记住一个公式，而余弦定理的计算稍复杂，需要使用开方和乘法等运算。

3.3 精度误差由于余弦定理中涉及到平方运算，可能会带来一定的误差，而正弦定理中没有涉及到平方运算，计算结果更加准确。

3.4 应用场景正弦定理在计算不规则三角形的边长和角度时较为常用，尤其适用于已知两边和夹角的情况。

而余弦定理在计算不规则三角形的边长和角度时同样常用，特别适用于已知三边的情况。

正弦定理、余弦定理知识点总结及证明方法1．掌握正弦定理、 余弦定理，并能解决一些简单的三角形胸怀问题．2．能够运用正弦定理、 余弦定理等知识和方法解决一些与丈量和几何计算相关的实质问题．主要考察相关定理的应用、三角恒等变换的能力、运算能力及转变的数学思想．解三角形经常作为解题工具用于立体几何中的计算或证明，或与三角函数联系在一同求距离、高度以及角度等问题，且多以应用题的形式出现．1． 正弦定理(1) 正弦定理：在一个三角形中， 各边和它所对角的正弦的比相等， 即 ．其 中 R 是三角形外接圆的半径．(2) 正弦定理的其余形式：， c① a ＝ R A ， b ＝2 sin＝；a②sin A ＝2R ， sin B ＝，sin C ＝ ；③a ∶b ∶c ＝______________________.2． 余弦定理——王彦文 青铜峡一中(1) 余弦定理：三角形中任何一边的平方等于其余两边的平方的和减去这两边与它们的夹角的余弦的积的两倍．即a 2＝，b 2＝，c 2＝.，即为勾若令 C ＝°，则 c 2＝90股定理．(2) 余 弦 定 理 的 变 形 ： cosA＝ ， cosB ＝ ，cosC ＝ .若 C 为锐角，则 cosC>0，即 a 2＋ b 2 ______c 2；若 C 为钝角，则 cosC<0，即 a 2＋b 2______c 2. 故由 a 2 ＋b 2 与 c 2 值的大小比较，能够判断 C 为锐角、钝角或直角．(3) 正、余弦定理的一个重要作用是实现边角____________，余弦定理亦能够写成 sin 2A＝ sin 2B ＋ sin 2C － 2sin Bsin CcosA ，近似地，sin 2B ＝ ____________ ； sin 2C ＝__________________.注意式中隐含条件 A ＋ B ＋C ＝π.3． 解斜三角形的种类(1) 已知三角形的随意两个角与一边，用____________定理．只有一解．(2) 已知三角形的随意两边与此中一边的对 角 ， 用 ____________ 定 理 ， 可 能 有___________________．如在△ ABC 中，已知 a ， b 和 A 时，解的状况如表：A 为钝角A 为锐角或直角图 形关 a ＝ b A aa ≥b a b 系 b A sin <b> 式 sin <解 的 ① ② ③ ④ 个 数(3) 已知三边，用 ____________定理．有1解时，只有一解．(4) 已知两边及夹角，用 ____________定理，必有一解．4． 三角形中的常用公式或变式(1) 三角形面积公式 S △＝ ＝＝ ____________ ＝ ____________ ＝____________．此中 R ，r 分别为三角形外接圆、内切圆半径．，(2) A ＋ B ＋ C ＝π，则 A ＝__________A＝ __________ ， 从 而sin A ＝2____________，cosA ＝ ____________ ， tan A ＝____________；A Asin 2＝ __________， cos 2＝__________，Atan 2 ＝ ________.tan A ＋ tan B ＋ tan C ＝__________.(3) 若三角形三边 a ，b ，c 成等差数列，则b ＝____________? 2sin B ＝____________?2B A －C A ＋ C A － C A2sin 2＝ cos2 ? 2cos 2 ＝ cos 2 ? tan 2C 1tan 2＝3.【自查自纠】． a bc R1(1)sin A ＝ sin B ＝sin C ＝ 2R BRC ② bc(2) ①2 si2 siRR2 2③ s in A ∶sin B ∶sin C2． (1) b 2＋c 2－2bccosA c 2＋a 2－ 2cacosB a 2 ＋b 2－2abcosC a 2＋ b 2b 2 ＋c 2－a 2c 2＋a 2－b 2a 2 ＋b 2－c 2>(2)2ca2ab2bc<(3) 互化sin 2C ＋sin 2A －2sin Csin AcosBsin 2A ＋ sin 2B －2sin Asin BcosC3．(1) 正弦 (2) 正弦 一解、两解或无解①一解 ②二解 ③一解 ④一解 (3) 余弦 (4) 余弦．11 1 abc(1) ab sin C bc s inA ac s in B2 22R412( a ＋b ＋c) rπ B ＋C(2) π－ ( B ＋ C)2 － 2sin( B ＋C－cos( B ＋C) )－ tan( B ＋ C cos B ＋CsinB ＋ C) 2 21 B ＋Ctan 2A B C (3)a ＋ csin A ＋ sin C tan tan tan2在△ABC中， A B 是A B 的()>sin >sinA．充足不用要条件B．必需不充足条件C．充要条件D．既不充足也不用要条件解：因为在同一三角形中，角大则边大，边大则正弦大，反之也成立，故是充要条件．故选 C.在△ABC中，已知 b＝， c＝，B＝°，则61030解此三角形的结果有 ()A．无解B．一解C．两解D．一解或两解解：由正弦定理知 sin C＝c·sin B5b＝6，又由c>b>csin B知， C有两解．也可依已知条件，画出△ ABC，由图知有两解．应选 C.( 2013·陕西 ) 设△ ABC的内角 A, B, C所对的边分别为 a, b, c,若b cos C＋ c cos B＝a sin A,则△ ABC的形状为()A．锐角三角形B．直角三角形C．钝角三角形D．不确立C＋解：由已知和正弦定理可得BC B ＝A· A ，即sin cos＝sin sin sin sin( B ＋C cos A)sinA A，亦即sinA＝A因为Aπ，sin sin sin.0< <π所以 sin A＝1，所以 A＝ 2.所以三角形为直角三角形．应选.B( 2012·陕西 ) 在△ ABC中，角 A，B，C 所对的π边分别为 a，b，c. 若 a＝2，B＝6，c＝23，则 b＝________．解：由余弦定理知b2＝a2＋c2－ 2accosB＝π222 ＋( 23)－2×2×2 3×cos 6＝ 4， b＝ 2.在△ABC中，角A，B，C 所对的边分别为a，b，c，若 a＝ 2，b＝2，sin B＋cosB＝ 2，则角 A 的大小为 ________．解：∵ sin B＋ cosB＝2，ππ∴2sin B＋4＝ 2，即 sin B＋4＝1.πππ又∵ B∈(0 ，π ) ，∴ B＋4＝2， B＝4 .a b依据正弦定理sin A＝sin B，可得sin A＝asin B1＝.b2ππ∵a＜b，∴ A＜B. ∴ A＝6 . 故填6 .种类一正弦定理的应用△ABC的内角A，B，C的对边分别为a，b，c，已知 A－ C＝90°， a＋ c＝ 2b，求 C.解：由 a＋c＝ b 及正弦定理可得sinA2＋s in C＝ 2sin B.又因为 A－ C＝90°， B＝180°－ ( A＋ C) ，故 cosC＋ sin C＝ sin A＋sin C＝ 2sin( A＋ C) ＝2sin(90 °＋ 2C) ＝ 2sin2(45 °＋ C) ．∴2 sin(45° ＋C＝2 2 sin(45° ＋)C)cos(45 °＋ C) ，41即 cos(45 °＋ C) ＝2.又∵ 0°＜ C＜90°，∴ 45°＋ C＝60°，C ＝15°.【评析】利用正弦定理将边边关系转变为角角关系，这是解本题的重点．( 2012·江西 ) 在△ ABC中，角 A，B，C 的对边分别为a， b，c已知 A＝π，bsinπ＋C －.44c sinπ＋B ＝a4.π(1)求证： B－C＝2；(2)若 a＝ 2，求△ ABC的面积．解：(1)证明：对bπ＋C－sin4csin π＋ B＝ a应用正弦定理得4B π＋ C －sinCπ＋B ＝sinA，sin sin4sin422即sin B2 sin C＋2 cosC－sinC222，整理得 B C2 sin B＋2 cosB ＝2sin cos －s in CcosB＝ 1，即 sin ( B－C)＝1.3ππ因为 B，C∈ 0，4，∴ B－C＝2 .3π，又由 (1)知 B－C(2) ∵ B＋ C＝π－ A＝4π＝2，5ππ∴B＝8，C＝8.∵a＝2，A＝πb＝，∴由正弦定理知4a Bπa Cπsin5sinsin A＝ 2sin8，c＝sin A＝2sin 8 .115ππ∴S△ABC＝2bcsin A＝2×2sin8×2sin 8×225ππππ2＝ 2sin8 sin 8＝ 2cos8 sin8＝2π 1sin 4＝2.种类二 余弦定理的应用1 3 3∴S △ABC ＝2acsin B ＝ 4 .【评析】①依据所给等式的构造特色利用余弦定理将角化边进行变形是快速解答本题的 重点．②娴熟运用余弦定理及其推论，同时还 要注意整体思想、方程思想在解题过程中的运 用．在△ ABC 中，a ，b ，c 分别是角 A ，B ，C 的对边，cosBb且cosC ＝－ 2a ＋c .(1) 求 B 的大小；(2) 若 b ＝ 13，a ＋c ＝4，求△ ABC 的面积．a 2＋ c 2－b 2， 解：(1) 由余弦定理知， cosB ＝ac2cosC ＝ a 2＋b 2－ c 2cosB b 2ab ，将上式代入cos C ＝－ a ＋c2 得a 2 ＋c 2－b 2 abb2＝－ a ＋c ， ac·a 2＋b 2－c22整理得 a 2＋c 2－ b 2＝－ ac.a 2＋c 2－b 2 －ac 1 ∴cosB ＝ ac ＝ ac ＝－ .22 22∵B 为三角形的内角，∴ B ＝ 3π.(2) 将 b ＝ 13，a ＋c ＝4，B ＝23π 代入 b 2＝a 2＋ c 2－2accosB ，得 13＝42－ 2ac －2accos 2 3π，解得 ac ＝3.若△ ABC 的内角 A ，B ，C 所对的边 a ，b ，c 知足( a ＋b) 2－ c 2＝4，且 C ＝60°，则 ab 的值为 ( )4A. 3B ．8－4 3C ． 12D.3解：由余弦定理得 c 2＝ a 2 ＋b 2－2abcosC ＝a 2＋b 2－ab ，代入 ( a ＋ b) 2－ c 2 ＝4 中得 ( a ＋ b) 24－ ( a 2＋b 2－ab) ＝ 4，即 3ab ＝ 4，∴ ab ＝3. 应选A.6种类三正、余弦定理的综合应用以用余弦定理化边后用不等式求最值．( 2013·全国新课标Ⅱ ) △ ABC的内角A、B、 C的对边分别为 a，b，c，已知 a＝bcosC＋ csin B.(1)求 B；(2)若 b＝2，求△ ABC面积的最大值．解： (1) 由已知及正弦定理得 sin A＝sin BcosC＋ sin Csin B. ①又 A＝π－ ( B＋ C) ，故sin A ＝ sin( B ＋ C) ＝ sin BcosC ＋cosBsin C. ②由①，②和 C∈(0 ，π ) 得 sin B＝ cosB.π又 B∈(0 ，π ) ，所以 B＝4 .12(2) △ ABC的面积 S＝2acsin B＝4 ac.由已知及余弦定理得 4 ＝ a2＋ c2－π2accos 4 .又 a2＋ c2≥2ac，故 ac≤4，2－ 2当且仅当 a＝c 时，等号成立．所以△ ABC面积的最大值为2＋1.【评析】(1) 化边为角与和角或差角公式的正向或反向多次联用是常用的技巧； (2) 已知边及其对角求三角形面积最值是高考取考过多次的问题，既可用三角函数求最值，也可( 2013·山东 ) 设△ ABC的内角 A，B，C 所对的边分别为a，b，c，且 a＋ c＝ 6， b＝ 2， cosB7＝9.(1)求 a，c 的值；(2)求 sin( A－ B) 的值．解： (1) 由余弦定理 b2＝a2＋ c2－2accosB，得 b2＝( a＋c) 2－2ac(1 ＋cosB) ，又 a＋ c ＝6，b＝2，7cosB＝9，所以 ac＝9，解得 a＝3，c＝3.242(2) 在△ ABC中， sin B＝ 1－cos B＝9 ，asin B 22由正弦定理得 sin A＝b＝ 3 .因为 a＝c，所以 A 为锐角，21所以 cosA＝1－sin A＝3.所以 sin( A－B) ＝sin AcosB－ cosAsin B＝10 227.种类四 判断三角形的形状后进行三角函数式的恒等变形，找出角之间的 关系；或将角都化成边，而后进行代数恒等变 形，可一题多解，多角度思虑问题，进而达到 对知识的娴熟掌握．在三角形 ABC 中，若 tan A ∶tan B ＝a 2∶b 2，试判断三角形 ABC 的形状．a 2 sin 2A解法一：由正弦定理，得 b 2＝sin 2B ， tan A sin 2 A所以 tan B ＝sin 2 B ，A Bsin 2AA ＝ Bsin cos2 ，即sin2所以cosAsin B ＝sinB sin2 . 所以 A ＝ B ，或2 A ＋B ＝π，所以 A ＝B2 22π或 A ＋ B ＝ 2 ，进而△ ABC 是等腰三角形或直角三角形．a2sin 2A解法二：由正弦定理，得 b 2＝ sin 2B ，所以tan A sin 2A cosB sin Atan B ＝sin 2B，所以 cosA ＝ sin B，再由正、余弦a 2＋ c 2 －b 2aca a 2－ b2c 2－定理，得 2 22 2 )( b ＋ c －a ＝ b ，化简得 (2bca 2－b 2 )＝ ，即 a 2＝ b 2 或c 2＝ a 2 ＋b 2. 进而△ ABC 是等腰三角形或直角三角形．【评析】由已知条件，可先将切化弦，再联合正弦定理，将该恒等式的边都化为角，然( 2012·上海 ) 在 △ABC 中 ， 若 sin 2A ＋sin 2B 2C ，则△ ABC 的形状是 ( )<sin A ．锐角三角形 B ．直角三角形C ．钝角三角形D ．不可以确立解：在△ ABC 中，∵ sin 2A ＋sin 2 B<sin 2C ，∴由正弦定理知 a 2 ＋b 2<c 2. ∴cos C ＝ a 2＋b 2－c 22ab<0，即∠ C 为钝角，△ ABC 为钝角三角形． 应选 C.种类五 解三角形应用举例某港口 O 要将一件重要物件用小艇送到一艘正在航行的轮船上．在小艇出发时，轮船位于港口 O北偏西 30°且与该港口相距20 n mile的A 处，并以 30 n mile/h的航行速度沿正东方向匀速行驶．假定该小艇沿直线方向以v n mile/h 的航行速度匀速行驶，经过 t h 与轮船相遇．(1)若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？(2)假定小艇的最高航行速度只好达到 30 n mile/h ，试设计航行方案 ( 即确立航行方向和航行速度的大小 ) ，使得小艇能以最短时间与轮船相遇，并说明原因．解法一：(1) 设相遇时小艇航行的距离为 S n mile ，则S＝900t 2＋400－2·30t ·20·cos（90°－ 30°）＝t2－t ＋400＝900600900 t －123＋300，1103故当 t ＝3时，S min＝103，此时 v＝1＝3 303.即小艇以 30 3 n mile/h的速度航行，相遇时小艇的航行距离最小．(2)设小艇与轮船在 B 处相遇，则v2 t 2＝400＋t 2－900 2·20·30t ·cos(90 °－ 30°) ，2600400故 v ＝ 900－t＋t2.v≤，∴6004002－＋≤，即∵0<30900t t900t3－t≤0，22解得 t ≥3. 又 t ＝3时，v＝30. 故 v＝ 30 时，2t 获得最小值，且最小值等于3.此时，在△ OAB中，有 OA＝OB＝AB＝20，故可设计航行方案以下：航行方向为北偏东30°，航行速度为 30 n mile/h ，小艇能以最短时间与轮船相遇．解法二：(1) 若相遇时小艇的航行距离最小，又轮船沿正东方向匀速行驶，则小艇航行方向为正北方向．设小艇与轮船在C处相遇．在 Rt△OAC中， OC＝20cos30°＝ 10 3，AC＝20sin30 °＝ 10.又 AC＝30t ，OC＝vt ，101103此时，轮船航行时间 t ＝30＝3，v＝1＝330 3.即小艇以 30 3 n mile/h的速度航行，相遇时小艇的航行距离最小．(2)假定 v＝ 30 时，小艇能以最短时间与轮船在 D处相遇，此时 AD＝DO＝30t .又∠ OAD＝60°，所以 AD＝ DO＝OA＝20，2解得 t ＝3.据此可设计航行方案以下：航行方向为北偏东 30°，航行速度的大小为30 n mile/h. 这样，小艇能以最短时间与轮船相遇．证明以下：如图，由 (1) 得 OC＝103， AC＝10，故 OC>AC，且关于线段 AC上随意点 P，有OP≥ OC>AC.而小艇的最高航行速度只好达到30 n mile/h ，故小艇与轮船不行能在 A，C 之间 ( 包括 C) 的随意地点相遇．设∠ COD＝θ (0 °<θ<90°) ，则在 Rt△COD 中，103CD＝103tan θ， OD＝cosθ .因为从出发到相遇，轮船与小艇所需要的10＋10 3tan θ和 t ＝103，时间分别为 t ＝30vcosθ10＋10 3tan θ10 3所以30＝vcosθ.153由此可得，v＝sin （θ＋30°）.3又 v≤30，故 sin( θ＋30°) ≥2，进而，30°≤ θ<90°.因为θ＝30°时， tan θ获得最小值，且3最小值为3 .10＋103tan θ于是，当θ＝30°时，t ＝302获得最小值，且最小值为3.【评析】①这是一道相关解三角形的实质应用题，解题的重点是把实质问题抽象成纯数学识题，依据题目供给的信息，找出三角形中的数目关系，而后利用正、余弦定理求解．②解三角形的方法在实质问题中，有宽泛的应用．在物理学中，相关向量的计算也要用到解三角形的方法．最近几年的高考取我们发现以解三角形为背景的应用题开始成为热门问题之一．③不论是什么种类的三角应用问题，解决的重点都是充足理解题意，将问题中的语言表达弄理解，画出帮助剖析问题的草图，再将其归纳为属于哪种可解的三角形．④本题用几何方法求解也较简易．10( 2012·武汉 5月模拟 ) 如图，渔船甲位于岛屿A的南偏西 60°方向的 B 处，且与岛屿 A 相距 12 海里，渔船乙以 10 海里 / 小时的速度从岛屿 A 出发沿正北方向航行，若渔船甲同时从B 处出发沿北偏东α的方向追赶渔船乙，恰好用2 小时追上．(1)求渔船甲的速度；(2)求 sin α的值．解： (1)依题意，∠BAC＝°，A B＝，12012 AC＝× ＝2，在△ ABC中，由余弦定理知 BC 1022022∠ BAC＝2＋2－＝AB＋ AC－ AB·AC·12202cos2×12×20×cos120°＝ 784，BC＝ 28.所以渔船甲的速度为 v＝28＝14( 海里 / 小2时) ．(2)在△ ABC中， AB＝12，∠ BAC＝120°，BC＝ 28，AB ∠BCA＝α，由正弦定理得sinα＝BC12＝28，进而 sin α＝，即sin120 °sin ∠ BAC sin α12sin120 °3328＝14.1．已知两边及此中一边的对角解三角形时，要注意解的状况，提防漏解．2．在判断三角形的形状时，一般将已知条件中的边角关系利用正弦定理或余弦定理转变为角角关系 ( 注意应用 A＋ B＋ C＝π 这个结论 ) 或边边关系，再用三角变换或代数式的恒等变形( 如因式分解、配方等 ) 求解，注意等式两边的公因式不要约掉，要移项提取公因式，不然有可能遗漏一种形状．3．要熟记一些常有结论，如三内角成等差数列，则必有一角为60°；若三内角的正弦值成等差数列，则三边也成等差数列；内角和定理与引诱公式联合产生的结论：sin A＝ sin( BA B＋C ＋C) ，cosA＝－ cos( B＋ C) ，sin 2＝cos 2，sin2 A＝－ sin2( B＋C) ，cos2A＝ cos2( B＋C) 等．4．应用正、余弦定理解斜三角形应用题的一般步骤：(1)剖析：理解题意，分清已知与未知，画出表示图；(2)建模：依据已知条件与求解目标，把已11知量与求解量尽量集中到一个三角形中，成立一个解斜三角形的模型；(3)求解：利用正、余弦定理有序地解出三角形，求得数学模型的解；(4)查验：查验上述所求得的解能否切合实际意义，进而得出实质问题的解．5．正、余弦定理是应用极为宽泛的两个定理，它将三角形的边和角有机地联系起来，进而使三角与几何产生联系，为求与三角形相关的量( 如面积、外接圆、内切圆半径和面积等 ) 供给了理论依照，也是判断三角形形状、证明三角形中相关等式的重要依照．主要方法有：化角法，化边法，面积法，运用初等几何法．注意领会此中蕴涵的函数与方程思想、等价转变思想及分类议论思想．12。

正弦定理与余弦定理知识集结知识元正弦定理公式知识讲解1．正弦定理【知识点的知识】1．正弦定理和余弦定理定理正弦定理余弦定理内容＝2R（R是△ABC外接圆半径）a2＝b2+c2﹣2bc cos A，b2＝a2+c2﹣2ac cos B，c2＝a2+b2﹣2ab cos C 变形形式①a＝2R sin A，b＝2R sin B，c＝2R sin C；②sin A＝，sin B＝，sin C＝；③a：b：c＝sin A：sin B：sin C；④a sin B＝b sin A，b sin C＝c sin B，a sin C＝c sin Acos A＝，cos B＝，cos C＝解决三角形的问题①已知两角和任一边，求另一角和其他两条边；②已知两边和其中一边的对角，求另一边和其他两角①已知三边，求各角；②已知两边和它们的夹角，求第三边和其他两角在△ABC 中，已知a ，b 和角A 时，解的情况A 为锐角A 为钝角或直角图形关系式a ＝b sin A b sin A ＜a ＜ba ≥b a ＞b 解的个数一解两解一解一解由上表可知，当A 为锐角时，a ＜b sin A ，无解．当A为钝角或直角时，a ≤b ，无解．2、三角形常用面积公式1．S ＝a •h a （h a 表示边a 上的高）；2．S ＝ab sin C ＝ac sin B ＝bc sin A ．3．S ＝r （a +b +c ）（r 为内切圆半径）．【正余弦定理的应用】1、解直角三角形的基本元素．2、判断三角形的形状．3、解决与面积有关的问题．4、利用正余弦定理解斜三角形，在实际应用中有着广泛的应用，如测量、航海、几何等方面都要用到解三角形的知识（1）测距离问题：测量一个可到达的点到一个不可到达的点之间的距离问题，用正弦定理就可解决．解题关键在于明确：①测量从一个可到达的点到一个不可到达的点之间的距离问题，一般可转化为已知三角形两个角和一边解三角形的问题，再运用正弦定理解决；②测量两个不可到达的点之间的距离问题，首先把求不可到达的两点之间的距离转化为应用正弦定理求三角形的边长问题，然后再把未知的边长问题转化为测量可到达的一点与不可到达的一点之间的距离问题．（2）测量高度问题：解题思路：①测量底部不可到达的建筑物的高度问题，由于底部不可到达，因此不能直接用解直角三角形的方法解决，但常用正弦定理计算出建筑物顶部或底部到一个可到达的点之间的距离，然后转化为解直角三角形的问题．②对于顶部不可到达的建筑物高度的测量问题，我们可选择另一建筑物作为研究的桥梁，然后找到可测建筑物的相关长度和仰、俯角等构成三角形，在此三角形中利用正弦定理或余弦定理求解即可．点拨：在测量高度时，要理解仰角、俯角的概念．仰角和俯角都是在同一铅锤面内，视线与水平线的夹角．当视线在水平线之上时，成为仰角；当视线在水平线之下时，称为俯角．例题精讲正弦定理公式例1.已知△ABC中，角A，B，C所对的边分别是a，b，c．若A=45°，B=30°，a=，则b=（）A．B．1C．2D．例2.在△ABC中，角A，B，C的对边分别为a，b，c，若，则B=（）A．B．C．D．或例3.在△ABC中，已知三个内角为A，B，C满足sin A：sin B：sin C=3：5：7，则C=（）A．90°B．120°C．135°D．150°利用正弦定理解三角形知识讲解【正余弦定理的应用】1、解直角三角形的基本元素．2、判断三角形的形状．3、解决与面积有关的问题．4、利用正余弦定理解斜三角形，在实际应用中有着广泛的应用，如测量、航海、几何等方面都要用到解三角形的知识例题精讲利用正弦定理解三角形例1.在△ABC中，a，b，c是内角A，B，C所对的边．若a>b，则下列结论不一定成立的（）A．A>B B．sin A>sin BC．cos A<cos B D．sin2A>sin2B例2.在△ABC中，角A，B，C的对边分别是a，b，c，且，则角A的大小为（）A．B．C．D．例3.在△ABC 中，三内角A ，B ，C 的对边分别为a ，b ，c ，若sin B =b sin A ，则a =（）A．B ．C ．1D ．三角形面积公式的简单应用知识讲解1．余弦定理【知识点的知识】1．正弦定理和余弦定理定理正弦定理余弦定理内容＝2R（R 是△ABC 外接圆半径）a 2＝b 2+c 2﹣2bc cos A ，b 2＝a 2+c 2﹣2ac cos B ，c 2＝a 2+b 2﹣2ab cos C变形形式①a ＝2R sin A ，b ＝2R sin B ，c ＝2R sin C ；②sin A ＝，sin B ＝，sin C ＝；③a ：b ：c ＝sin A ：sin B ：sin C ；④a sin B ＝b sin A ，b sin C ＝c sin B ，a sin C ＝c sin A cos A ＝，cos B ＝，cos C ＝解决三角形的问题①已知两角和任一边，求另一角和其他两条边；②已知两边和其中一边的对角，求另一边和其他两角①已知三边，求各角；②已知两边和它们的夹角，求第三边和其他两角在△ABC 中，已知a ，b 和角A 时，解的情况A 为锐角A 为钝角或直角图形关系式a ＝b sin A b sin A ＜a ＜ba≥ba ＞b 解的个数一解两解一解一解由上表可知，当A 为锐角时，a ＜b sin A ，无解．当A 为钝角或直角时，a ≤b ，无解．例题精讲三角形面积公式的简单应用例1.已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c，且（a +b ）2=c 2+ab ，B =30°，a =4，则△ABC 的面积为（）A ．4B ．3C ．4D ．6例2.设△ABC 的三个内角A ，B ，C 成等差数列，其外接圆半径为2，且有，则三角形的面积为（）A ．B ．C ．或D ．或例3.在△ABC中角ABC的对边分别为a、b、c，cos C=，且a cos B+b cos A=2，则△ABC面积的最大值为（）A．B．C．D．利用余弦定理解三角形当堂练习填空题练习1.如图，O在△ABC的内部，且++3=，则△ABC的面积与△AOC的面积的比值为_____．练习2.锐角△ABC的内角A，B，C的对边分别为a，b，c，已知c2-8=（a-b）2，a=2c sin A，则△ABC的面积为____．练习3.在△ABC中，内角A，B，C的对边分别为a，b，c，已知，则的最大值是____．解答题练习1.'在△ABC中，角A，B，C所对的边分别为a，b，c，且满足．（1）求角B的大小；的最大值．（2）若D为AC的中点，且BD=1，求S△ABC'练习2.'在△ABC中，角A、B、C的对边分别是a、b、c，若（a+c）sin B-b sin C=b cos A．（1）求角A；（2）若△ABC的面积为4，a=6，求△ABC的周长．'练习3.'△ABC内角A，B，C所对的边分别为a，b，c．若。

三角函数五——正、余弦定理一、知识点 （一）正弦定理：2,sin sin sin a b cR A B C===其中R 是三角形外接圆半径. 变形公式：（1）化边为角：2sin ,2sin ,2sin ;a R A b R B c R C ===a b c3sin B C4（（（解可 2、余弦定理可以解决的问题： （1）已知三边，求三个角；（解唯一）（2）已知两边和它们的夹角，求第三边和其他两个角；（解唯一）：（3）两边和其中一边对角，求另一边，进而可求其它的边和角.（解可能不唯一）三、正、余弦定理的应用射影定理：cos cos ,cos cos ,cos cos .a b C c B b a C c A c a B b A =+=+=+有关三角形内角的几个常用公式 解三角形常见的四种类型（1）已知两角,A B 与一边a ：由180A B C ++=︒及正弦定理sin sin sin a b cA B B==，可 求出C ∠，再求,b c 。

（2）已知两边,b c 与其夹角A ，由2222cos a b c bc A =+-，求出a ，再由余弦定理， 求出角,B C 。

（3）已知三边a b c 、、，由余弦定理可求出A B C ∠∠∠、、。

（4讲解 （知∆A ∠,A ．由a c ==,075C ∠=,所以030B ∠=,1sin 2B =由正弦定理得1sin 2sin 2a b B A =⋅==,故选A（2013·新课标Ⅰ高考文科·Ｔ10）已知锐角△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，02cos cos 232=+A A ，7=a ，c=6，则=b （ ） A.10B.9C.8D.5【解题指南】由02cos cos 232=+A A ，利用倍角公式求出A cos 的值，然后利用正弦定理或余弦定理求得b 的值.【解析】选D.因为02cos cos 232=+A A ，所以01cos 2cos 2322=-+A A ，解得251cos 2=A ， 方法一:因为△ABC 为锐角三角形，所以51cos =A ,562sin =A . 由正弦定理C cA a sin sin =得，C sin 65627=.6sin =C 所以sin =B5.方法二5∴sin 9、（)0C =，求边又1+即12cos 0A -=，2，又0°<A<180°，所以A ＝60°.在△ABC 中，由正弦定理sin sin a b A B =得sin 2sin 2b A B a ===， 又∵b a <，所以B ＜A ，B ＝45°，C ＝75°，∴BC 边上的高AD 752sin(4530)=+在锐角△ABC 中,内角A,B,C 的对边分别为a,b,c ,且 b.(1)求角A 的大小.(2)若a=6,b+c=8,求△ABC 的面积.【解题指南】(1)由正弦定理易求角A 的大小;(2)根据余弦定理,借助三角形的面积公式求解.【解析】(1)由及正弦定理sin sin a bA B=,得, 因为(2)b 2+c 26、（3,则c =.4、（2012福建文）在ABC ∆中,已知60,45,BAC ABC BC ∠=︒∠=︒=,则AC =_______.【解析】由正弦定理得sin 45AC AC =⇒=︒5、（2011北京）在ABC 中，若15,,sin 43b B A π=∠==，则a = .【答案】325 【解析】：由正弦定理得sin sin a b A B =又15,,sin 43b B A π=∠==所以5,13sin 34a a π==1、在△ABC 中，角,,A B C 的对边分别为,,abc ，3A π=,1a b ==，则c =（ ）A 、1B 、2 C1 D 、32、在△ABC 中，分别为的对边.如果成等差数列，30°，△ABC 的面 A 、3）75213 C D 4B π=，则___________________.3，＝60°AB 的长度等于13（20132012天津理）在ABC ∆中,内角A ,B ,C 所对的边分别是,,a b c ,已知8=5b c ,=2C B ,则cos C =(）A ．725B ．725-C ．725±D ．2425【答案】A【解析】85,b c =由正弦定理得8sin 5sin B C =，又2C B =，8sin 5sin 2B B ∴=，所以8sin 10sin cos B B B =，易知247sin 0,cos ,cos cos 22cos 1525B B C B B ≠∴===-=（2013·湖南高考文科·Ｔ5）在锐角∆ABC 中，角A ，B 所对的边长分别为a ，b. 若2asinB=3b ，则角A 等于（ ） A.3π B.4π C.6π D.12π【解题指南】本题先利用正弦定理B bA a sin sin =化简条件等式，注意条件“锐角三角形” .【解析】选A.由2asinB=3b 得2sinAsinB=3sinB,得sinA=23,所以锐角A=3π. （2013·湖南高考理科·Ｔ3）在锐角ABC ∆中，角,A B 所对的边长分别为,a b .若2sin ,a B A =则角等于A ．12π（2013 A . 3 5,=在△B 0=. (1)(2)若a 【解题指南】(1)借助三角形内角和为π，结合三角恒等变换将条件中的等式转化为只含B 的方程，求出B 的三角函数值，进而可求出角B.（2）根据（1）求出的B 与a c 1+=，由余弦定理可得b 2关于a 的函数，注意到a c 1+=可知0a 1<<，进而可求出b 的范围.【解析】（1）由已知得cos(A B)cos A cos B A cos B 0-++-=，即sin Asin B A cos B 0=.因为sin A 0≠，所以sin B B 0=,又cosB 0≠,所以tan B =,又0B <<π，所以B 3π=.（2）由余弦定理，有222b a c 2accos B =+-，因为a c 1+=，1cos B 2=,所以2211b 3(a )24=-+，又因为0a 1<<，所以21b 14≤<，即1b 12≤<.1sin BAM ∠=∠（2013·上海高考文科·T5）已知∆ABC 的内角A 、B 、C 所对的边分别是a 、b 、c.若a +ab+b 2-c 2=0，则角C 的大小是 .【解析】π32212- cos 0- 222222=⇒-=+=⇒=++C ab c b a C c b ab a 【答案】π32设ABC ∆的内角A ，B ，C 的对边分别为c b a ,,，ac c b a c b a =+-++))((（I ）求B ; （II ）若413sin sin -=C A ,求C . 【解题指南】（I ）由条件ac c b a c b a =+-++))((确定求B 应采用余弦定理. （II ）应用三角恒等变换求出C A +及C A -的值，列出方程组确定C 的值. 【解析】（I ）因为ac c b a c b a -=+-++))((.所以ac b c a -=-+222.222（II 221+=故-C A10、（（I c = 所以A （2012（1（2【解析】（1） 3(cos cos sin sin )16cos cos 3cos cos 3sin sin 13cos()11cos()3BC B C B C B C B C B C A π+-=⎧⎪-=-⎪⎪+=-⎨⎪⎪-=-⎪⎩ 则1cos 3A =. （2）由（1）得sin A =,由面积可得bc=6①,则根据余弦定理2222291cos 2123b c a b c A bc +-+-===则2213b c +=②, ①②两式联立可得32b a =⎧⎪⎨=⎪⎩或32a b =⎧⎪⎨=⎪⎩ 7、（2011全国）△ABC 的内角A 、B 、C 的对边分别为a 、b 、c.己知sin csin sin sin a A C C b B +=.（I ）求B ； （Ⅱ）若75,2,A b ==a c 求，. 【解析】（I）由正弦定理得222a cb +=2222cos b a c ac B =+-cos 2B =45B =（II sin30=故6a +=60645c b ==1、∆C 的对边分别为 ）2 A A 、30° B 、30°或150° C 、60° D 、60°或120° 8、已知在△ABC 中,sin :sin :sin 3:2:4A B C =,那么cos C 的值为（ ）A 、14-B 、14C 、23- D 、2310、若△ABC 的内角，,,A B C 满足6sin 4sin 3sin A B C ==，则cos B =A B ．34C D ．111611、在ABC ∆中，角,,A B C 所对的边分,,a b c ．若cos sin a A b B =，则2sin cos cos A A B +=A ．-12 B ．12C ． -1D ．112、已知在△ABC 中，10,a b A ===45°,则B = 。

1.1～1.2正弦定理、余弦定理要点解读一、正弦定理1．正弦定理及其证明在一个三角形中，各边和它所对角的正弦的比相等，即sin sin sin a b c A B C==． 课本利用三角形中的正弦函数的定义和向量的数量积两种方法证明了正弦定理，同学们可以思考一下有没有别的方法呢？答案是肯定的．证明如下：当ABC △为锐角三角形时（如图所示），过点A 作单位向量i 垂直于AB ，因为AC AB BC =+，所以()AC AB BC AB BC =+=+····i i i i ，cos(90)0cos(90)b A a B -=+-°°，即sin sin b A a B =，得sin sin a b A B=． 当ABC △为钝角或直角三角形时也可类似证明．2．正弦定理常见变形公式（1）sin sin sin sin b A c A a B C ==，sin sin sin sin c B a B b C A ==，sin sin sin sin a C b C c A B==； （2）::sin :sin :sin a b c A B C =；（3）2sin 2sin a R A b R B ==，，2sin c R C =（R 为ABC △外接圆的半径）；（4）sin 2a A R =，sin 2b B R =，sin 2c C R =； （5）sin sin sin sin sin sin a b c a b c A B C A B C++===++． 注：这些常见的变形公式应熟练掌握，在具体解题时，可根据不同的题设条件选择不同的变形公式．3．正弦定理的运用利用正弦定理，可以解决以下两类有关解三角形的问题：①已知两角和任意一边，求其他两边和另一角；②已知两边和其中一边的对角，求另一边的对角．二、余弦定理1．余弦定理及表达式三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍．2222c o s a b c b c A=+-；2222o s b c a c a B =+-； 2222c o s c a b a b C=+-． 注：余弦定理反映了a b c A B C ，，，，，元素间的动态结构，揭示了任意三角形的边、角关系．2．余弦定理的另一种表达形式222c o s 2b c a A bc+-=； 222c o s 2c a b B ac+-=； 222c o s 2a b c C ab +-=；注：若已知三边求角时，应用余弦定理的此表达形式简单易行．3．余弦定理的运用利用余弦定理，可以解决以下两类有关解三角形的问题：（1）已知三边，求三个角；（2）已知两边和它们的夹角，求第三边和其他两个角．注：这两类问题在有解时都只有一个解．4．勾股定理和余弦定理的区别与联系勾股定理指出了直角三角形中三边平方之间的关系，余弦定理则指出了一般三角形中三边平方之间的关系．由余弦定理及余弦函数的性质可知，如果一个三角形两边的平方和等于第三边的平方，那么第三边所对的角是直角；如果小于第三边的平方，那么第三边所对的角是钝角；如果大于第三边的平方，那么第三边所对的角是锐角．因此，勾股定理可以看作是余弦定理的特殊情况，余弦定理可以看作是勾股定理的推广．。

必修5第一章，三角函数 第一节 正弦定理1、正弦定理：在C ∆AB 中，a 、b 、c 分别为角A 、B 、C 的对边，R 为C ∆AB 的外接圆的半径，则有 ．2、正弦定理的变形公式：①2sin a R =A ， ，2sin c R C =；②sin 2a R A =，sin 2b R B = ，；③::__________________a b c =； ④sin sin sin sin sin sin a b c a b cC C++===A +B +A B ． （正弦定理主要用来解决两类问题：1、已知两边和其中一边所对的角，求其余的量。

2、已知两角和一边，求其余的量。

）3、对于已知两边和其中一边所对的角的题型要注意解的情况。

（一解、两解、无解三种情况） 如：在三角形ABC 中，已知a 、b 、A （A 为锐角）求B 。

具体的做法是：数形结合思想 第一类A 为锐角（1）.算出CD=bsinA,看a 的情况： （2） 当a<bsinA ，则B 无解，三角形不存在 （3） 当bsinA<a<b,则B 有两解，有两个三角形 （4）当a=bsinA 或a ≥b 时，B 有一解，有一个三角形 第二类 A 为钝角或是直角（1） b<a 则B 有一个解，有一个三角形 （2） b ≥a 则B 无解，不存在三角形 4、三角形面积公式：11sin sin _________22C S bc ab C ∆AB =A ==． 题型1、已知两角和一边，求其余的量1.在△ABC 中，已知a=8,6075B C ==，,则求三角形其他的要素D bsinAAbaC题型2.已知两边和其中一边所对的角，求其余的量1.△ABC中，已知a＝1，b＝3，A＝30°求三角形的其他要素2.△ABC中，已知a＝2，b＝2，A＝45°求B,C和c,‘3.△ABC中，已知a＝2，b＝2，B＝135°求A,C和c,题型3.不求解判断三角形一解、两解、无解三种情况a , b=4, 那么满足条件的△ABC ( ) 1．在△ABC中，∠A=60°23(A) 有一个解 (B) 有两个解 (C) 无解 (D)不能确定题型4.求三角形的面积题型5.边角互换，判断三角形的形状2、在△ABC中，已知a cosA=b cosB，则△ABC的形状是．3．在△ABC 中，=，则△ABC 是（ ）A ． 等腰三角形B ． 直角三角形C ． 等腰或直角三角形D ． 等边三角形第二节 余弦定理1、余弦定理：在C ∆AB 中，有2222cos a b c bc =+-A ，2_________________b =，2222cos c a b ab C =+-．2、余弦定理的推论：cos ____________A =，222cos 2a c b ac+-B =，222cos 2a b c C ab +-=．(余弦定理主要解决的问题：1、已知两边和夹角，求其余的量。

人教版高二数学上册必修5第一章正弦定理和余弦定理知识点
人教版高二数学上册必修5第一章正弦定理和
余弦定理知识点
学习是劳动，是充满思想的劳动。

查字典数学网为大家整理了第一章正弦定理和余弦定理知识点，让我们一起学习，一起进步吧！
余弦定理定义及公式余弦定理，是描述三角形中三边长度与一个角的余弦值关系的数学定理。

是勾股定理在一般三角形情形下的推广。

a=b+c-2bccosA
余弦定理证明
如上图所示，△ABC，在c上做高，根据射影定理，可得到：将等式同乘以c得到：
运用同样的方式可以得到：
将两式相加：
向量证明
正弦定理和余弦定理正弦定理
a/sinA=b/sinB=c/sinC=2R
（1）已知三角形的两角与一边，解三角形
（2）已知三角形的两边和其中一边所对的角，解三角形（3）运用a：b：c=sinA：sinB：sinC解决角之间的转换关系
直角三角形的一个锐角的对边与斜边的比叫做这个角的正。

高中数学正弦定理和余弦定理知识点(精选)高中数学正弦定理概述a/sinA=b/sinB=c/sinC=2R正弦定理(1)已知三角形的两角与一边，解三角形(2)已知三角形的两边和其中一边所对的角，解三角形(3)运用a：b：c=sinA：sinB：sinC解决角之间的转换关系直角三角形的一个锐角的对边与斜边的比叫做这个角的正弦。

[1]证明步骤1在锐角△ABC中，设BC=a，AC=b，AB=c。

作CH⊥AB垂足为点HCH=a·sinBCH=b·sinA∴a·sinB=b·sinA得到a/sinA=b/sinB同理，在△ABC 中，b/sinB=c/sinC步骤2.证明a/sinA=b/sinB=c/sinC=2R：任意三角形ABC,作ABC的外接圆O.作直径BD交⊙O于D.连接DA因为在同圆或等圆中直径所对的圆周角是直角，所以∠DAB=90度因为在同圆或等圆中同弧所对的圆周角相等，所以∠D等于∠C.所以c/sinC=c/sinD=BD=2R类似可证其余两个等式。

高中数学余弦定理概述余弦定理是揭示三角形边角关系的重要定理，直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题，若对余弦定理加以变形并适当移于其它知识，则使用起来更为方便、灵活。

直角三角形的一个锐角的邻边和斜边的比值叫这个锐角的余弦值性质对于任意三角形，任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的两倍积，若三边为a，b，c 三角为A，B，C ，则满足性质——S △ABC=1/2absinS△ABC=1/2bcsinAS△ABC=1/2acsinB第一余弦定理(任意三角形射影定理)设△ABC的三边是a、b、c，它们所对的角分别是A、B、C，则有a=b·cos C+c·cos B， b=c·cos A+a·cos C， c=a·cos B+b·cos A。

③::sin :sin :sin a b c C =ΑΒ；④sin sin sin sin sin sin a b c a b c C C++===Α+Β+ΑΒ．3、三角形面积公式：111sin sin sin 222C S bc ab C ac ∆ΑΒ=Α==Β．4、余弦定理：在C ∆ΑΒ中，有2222cos a b c bc =+−Α，2222cos b a c ac =+−Β，2222cos c a b ab C =+−．5、余弦定理的推论：222cos 2b c a bc +−Α=，222cos 2a c b ac +−Β=，222cos 2a b c C ab+−=．6、设a 、b 、c 是C ∆ΑΒ的角Α、Β、C 的对边，则：①若222a b c +=，则90C =�；②若222a b c +>，则90C <�；③若222a b c +<，则90C >�．7、数列：按照一定顺序排列着的一列数．8、数列的项：数列中的每一个数．9、有穷数列：项数有限的数列．10、无穷数列：项数无限的数列．11、递增数列：从第2项起，每一项都不小于它的前一项的数列．12、递减数列：从第2项起，每一项都不大于它的前一项的数列．13、常数列：各项相等的数列．14、摆动数列：从第2项起，有些项大于它的前一项，有些项小于它的前一项的数列．15、数列的通项公式：表示数列{}n a 的第n 项与序号n 之间的关系的公式．16、数列的递推公式：表示任一项n a 与它的前一项1n a −（或前几项）间的关系的公式．17、如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，则这个数列称为等差数列，这个常数称为等差数列的公差．18、由三个数a ，Α，b 组成的等差数列可以看成最简单的等差数列，则Α称为a 与b 的等差中项．若2a cb +=，则称b 为a 与c 的等差中项．19、若等差数列{}n a 的首项是1a ，公差是d ，则()11n a a n d =+−．20、通项公式的变形：①()n m a a n m d =+−；②()11n a a n d =−−；③11n a a d n −=−；④11n a a n d −=+；⑤n m a a d n m −=−．21、若{}n a 是等差数列，且m n p q +=+（m 、n 、p 、*q ∈Ν），则m np q a a a a +=+；若{}n a 是等差数列，且2n p q =+（n 、p 、*q ∈Ν），则2n p q a a a =+．22、等差数列的前n 项和的公式：①()12n n n a a S +=；②()112n n n S na d −=+．23、等差数列的前n 项和的性质：①若项数为()*2n n ∈Ν，则()21n n n S n a a +=+，且S S n d −=偶奇，1n n S a S a +=奇偶．②若项数为()*21n n −∈Ν，则()2121n n S n a −=−，且n S S a −=奇偶，1S n S n =−奇偶（其中n S na =奇，()1n S n a =−偶）．24、如果一个数列从第2项起，每一项与它的前一项的比等于同一个常数，则这个数列称为等比数列，这个常数称为等比数列的公比．25、在a 与b 中间插入一个数G ，使a ，G ，b 成等比数列，则G 称为a 与b 的等比中项．若2G ab =，则称G 为a 与b 的等比中项．26、若等比数列{}n a 的首项是1a ，公比是q ，则11n n a a q−=．27、通项公式的变形：①n m n m a a q −=；②()11n n a a q −−=；③11n n a q a −=；④n m n m a q a −=．28、若{}n a 是等比数列，且m n p q +=+（m 、n 、p 、*q ∈Ν），则m n p q a a a a ⋅=⋅；若{}n a 是等比数列，且2n p q =+（n 、p 、*q ∈Ν），则2n p q a a a =⋅．29、等比数列{}n a 的前n 项和的公式：()()()11111111n n n na q S a q a a q q qq =⎧⎪=−⎨−=≠⎪−−⎩．30、等比数列的前n 项和的性质：①若项数为()*2n n ∈Ν，则S q S =偶奇．②n n m n m S S q S +=+⋅．③n S ，2n n S S −，32n n S S −成等比数列．31、0a b a b −>⇔>；0a b a b −=⇔=；0a b a b −<⇔<．32、不等式的性质：①a b b a >⇔<；②,a b b c a c >>⇒>；③a b a c b c >⇒+>+；④,0a b c ac bc >>⇒>，,0a b c ac bc ><⇒<；⑤,a b c d a c b d >>⇒+>+；⑥0,0a b c d ac bd >>>>⇒>；⑦()0,1n n a b a b n n >>⇒>∈Ν>；⑧)0,1a b n n >>⇒>∈Ν>．33、一元二次不等式：只含有一个未知数，并且未知数的最高次数是2的不等式．34、二次函数的图象、一元二次方程的根、一元二次不等式的解集间的关系：判别式24b ac ∆=−0∆>0∆=0∆<二次函数2y ax bx c =++()0a >的图象一元二次方程20ax bx c ++=()0a >的根有两个相异实数根1,2x =()12x x <有两个相等实数根122b x x a ==−没有实数根一元二次不等式的解集20ax bx c ++>()0a >{}12x x x x x <>或2b x x a ⎧⎫≠−⎨⎬⎩⎭R20ax bx c ++<()0a >{}12x x x x <<∅∅35、二元一次不等式：含有两个未知数，并且未知数的次数是1的不等式．36、二元一次不等式组：由几个二元一次不等式组成的不等式组．37、二元一次不等式（组）的解集：满足二元一次不等式组的x 和y 的取值构成有序数对(),x y ，所有这样的有序数对(),x y 构成的集合．38、在平面直角坐标系中，已知直线0x y C Α+Β+=，坐标平面内的点()00,x y Ρ．①若0Β>，000x y C Α+Β+>，则点()00,x y Ρ在直线0x y C Α+Β+=的上方．②若0Β>，000x y C Α+Β+<，则点()00,x y Ρ在直线0x y C Α+Β+=的下方．39、在平面直角坐标系中，已知直线0x y C Α+Β+=．①若0Β>，则0x y C Α+Β+>表示直线0x y C Α+Β+=上方的区域；0x y C Α+Β+<表示直线0x y C Α+Β+=下方的区域．②若0Β<，则0x y C Α+Β+>表示直线0x y C Α+Β+=下方的区域；0x y C Α+Β+<表示直线0x y C Α+Β+=上方的区域．40、线性约束条件：由x ，y 的不等式（或方程）组成的不等式组，是x ，y 的线性约束条件．目标函数：欲达到最大值或最小值所涉及的变量x ，y 的解析式．线性目标函数：目标函数为x ，y 的一次解析式．线性规划问题：求线性目标函数在线性约束条件下的最大值或最小值问题．可行解：满足线性约束条件的解(),x y ．可行域：所有可行解组成的集合．最优解：使目标函数取得最大值或最小值的可行解．41、设a 、b 是两个正数，则2a b +称为正数a 、b 的算术平均数，称为正数a 、b 的几何平均数．42、均值不等式定理：若0a >，0b >，则a b +≥，即2a b +≥．43、常用的基本不等式：①()222,a b ab a b R +≥∈；②()22,2a b ab a b R +≤∈；③()20,02a b ab a b +⎛⎞≤>>⎜⎟⎝⎠；④()222,22a b a b a b R ++⎛⎞≥∈⎜⎟⎝⎠．44、极值定理：设x 、y 都为正数，则有⑴若x y s +=（和为定值），则当x y =时，积xy 取得最大值24s ．⑵若xy p =（积为定值），则当x y =时，和x y +取得最小值．。