北航理论力学
- 格式:ppt
- 大小:1.76 MB
- 文档页数:26








理论力学绪论•什么是力学?•力学是怎样发展的?•理论力学的学习目的•理论力学的研究内容•理论力学的研究方法什么是力学?•力学是研究物体机械运动规律的科学。
•物体的机械运动是指物体的空间位形(位置和形状)随时间的变化。
–移动、转动、流动和变形•力学的研究为揭示自然界中与机械运动有关的规律提供了有效的工具,它也是近代工程技术的重要理论基础之一。
力学的发展始终是和人类社会活动紧密联系的,它的发展与完善推动了科学技术和社会的进步。
力学发展遵循认知规律指导实践并发现或提出新问题理性认识(或深入理性认识)感性认识(或初步理性认识)1、建筑与桥梁建于1056年山西应县木塔早期筒体结构建筑比萨斜塔建于1173-1370年观察竹子的特征竹子的横截面比萨斜塔横截面早期建筑的特点:高度低,跨度小,承载能力低,材料为砖石和木材。
赵州桥建于581-599 年跨度:37. 4m拱高:7m早期拱形结构建筑“敞肩拱”的运用为世界桥梁史上的首创,并有“世界桥梁鼻祖”的美誉。
现代筒体结构建筑高度:452米材料:钢筋混凝土吉隆坡双塔大厦建筑物高度增加会产生什么新问题?风载会引起高层建筑物的晃动双塔大厦利用结构阻尼减小塔体的晃动现代大跨度桥梁桥梁跨度增大又会产生什么新问题?美国华盛顿州塔科马悬索桥建造设计风速60m/s破坏时的风速19m/s 建于1940年,桥长853m事后分析引起桥梁振动的原因计算机模拟与仿真地震对建筑物的影响如何减小地震对建筑物的影响?建筑物减震的模拟实验研究美国旧金山国际机场新楼使用了移动地基2、机械手与机器人机械手在工业生产中的应用天津大学研制的医用缝合机械手六足步行机器人步行机器人的应用前景从分析研究人体的行走到双足步行机器人的实现,体现了力学、自动控制和计算机等科学技术的综合应用。
北京理工大学研制力学的发展-车辆与飞机3、车辆与飞机车辆的早期研制与应用早期的农用车辆现代车辆研究提出的要求:舒适、安全、高速、便捷、环保利用计算机分析车辆的动力学问题汽车自动驾驶的实验研究早期直升机—原理的认识现代直升机—科学技术的综合应用社会的发展与进步需要科学技术的不断发展与创新。

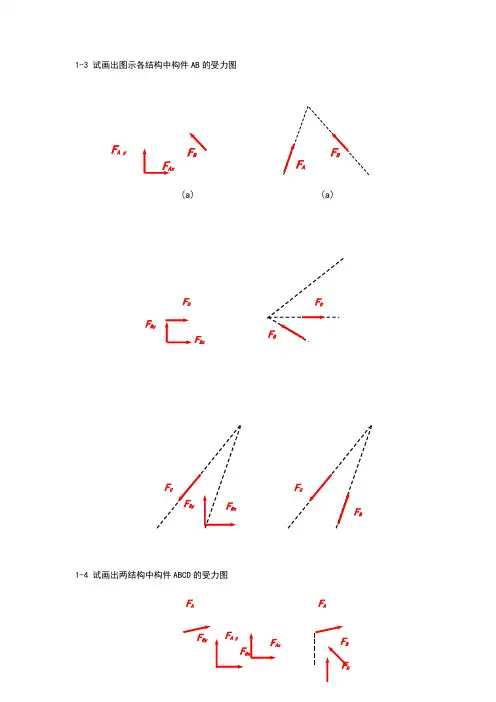
1-3 试画出图示各结构中构件AB 的受力图1-4 试画出两结构中构件ABCD 的受力图F AxF A yF B(a)(a)F DFBxF ByF AxF A yF ByF AF BxF A1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a1-5b1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
F AxF A y F DxF DyWT EF CxF C yWF AxF A yF BxF B yF CxF C yF DxF DyF BxF ByT EN’F BF DF A NF AF BF D解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:对C 点有:解以上二个方程可得:解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:对C 点由几何关系可知:解以上两式可得:2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):F ABF CDF BF C其中:。
对BC 杆有:。
A ,C 两点约束力的方向如图所示。
2-4四连杆机构在图示位置平衡,已知OA=60cm,BC=40cm,作用在BC 上力偶的力偶矩M 2=1N ·m 。
试求作用在OA 上力偶的力偶矩大小M 1和AB 所受的力。
951力学基础考试大纲注意:总分150分,理论力学部分占40%,材料力学部分占60%。
第一部分理论力学大纲静力学1、几何静力学(第1-3章)基本内容:静力学的基本公理,受力分析,力系简化的基本方法和有关力学量的基本计算,平衡方程的建立与求解,摩擦(滑动摩擦和滚动摩擦)问题,桁架内力的计算,平衡结构的静定性问题。
基本要求:深入理解静力学中有关的公理,熟练掌握刚体(刚体系)的受力分析,力系简化的基本方法和有关基本概念和基本量的计算,能够确定给定力系作用下独立平衡方程的数目,能够用定性和定量的方法研究刚体(刚体系)的平衡问题。
能够分析研究考虑摩擦时刚体或刚体系的平衡问题以及平面桁架的内力计算问题。
2、分析静力学(第4章)基本内容:各种力(重力、弹性力、有势力、摩擦力、合力、等效力系)的功,约束及其分类、广义坐标和自由度、虚位移与虚功、理想约束、虚位移原理及其应用、有势力作用下质点系平衡位置的稳定性。
基本要求:熟练计算各种力的功,能够确定系统的约束类型,确定系统的自由度和广义坐标,理解虚位移的基本概念,会判断约束是否是理想约束;能够熟练应用虚位移原理求解质点系平衡问题;会判断有势力作用下质点系平衡位置的稳定性。
动力学1、质点动力学(第五章)基本内容:质点的运动方程、速度、加速度的各种表示方法(矢量法、直角坐标法、自然坐标法)以及有关基本量的计算,质点运动微分方程,点的复合运动(三种运动分析、速度合成定理和加速度合成定理),质点相对运动动力学基本方程。
基本要求:熟练掌握质点运动方程、速度和加速度的各种表示方法和有关基本量的计算,能够熟练建立质点运动微分方程,对于简单的运动微分方程能够求解。
熟练应用点的复合运动的基本理论与方法研究点的复合运动(速度和加速度)问题,能够在非惯性参考系下建立质点相对运动动力学基本方程,具有对质点的运动学和动力学问题进行定性和定量分析的初步能力。
2、质点系动力学(第六章)基本内容:质点系的动量定理、变质量质点动力学方程、动量矩定理(包括对固定点、动点和质心的动量矩定理)、动能定理及其有关基本量的计算。
理论力学AII 期末考试模拟试题一、 选择题(将正确答案的字母填在空格内,每小题2分,共10分)1、对于具有定常约束的质点系,其动能T 最一般的形式可以表示成 的函数。
A :广义速度; B :广义坐标; C: 时间t2、定点运动的圆锥ABC 在水平固定圆盘上纯滚动,如图1所示。
若圆锥底面圆心D 作匀速圆周运动,则该圆锥的角加速度矢量α与角速度矢量ω的关系是 。
A :α平行于ω;B :α垂直于ω;C :为零矢量α;D :为非零矢量α图13、二自由度线性系统的振动周期与 有关。
A :广义质量;B :广义刚度;C :初始位置;D :初始速度4、只应用第二类拉格朗日方程 求出非自由质点系的约束力。
A :一定能; B :一定不能; C :不一定能5、第二类拉格朗日方程可用于研究具有 质点系的力学问题。
A :完整约束; B :定常约束; C :非完整约束; D :非定常约束 注:第二类拉格朗日方程为:),,2,1(d d k j Q q T q T t j j j " ==⎟⎟⎠⎞⎜⎜⎝⎛∂∂−⎟⎟⎠⎞⎜⎜⎝⎛∂∂。
其中k 为系统的自由度。
为对应于广义坐标的主动力的广义力。
j Q j q 二、 填空题(将最简结果填在空格内,每空5分,共50分)1、 质量为m 的质点M 可在半径为R 的圆环内运动,圆环以角速度ω(常矢量)绕AB 轴作定轴转动,如图2所示。
θ为质点的广义坐标,此时质点的动能可以表示成,其中012T T T T ++=)2,1,0(=i Ti g为广义速度的i 次齐次函数。
求:=2T =1T=0T图2 图32、长为L 质量为m 的均质杆OA 用光滑柱铰链悬挂在天花板上,下端与刚度系数为k 的水平弹簧连接,杆铅垂时弹簧为原长,如图3所示。
求系统在平衡位置附近作微幅摆动的动力学方程。
动力学方程: 。
3、圆盘相对正方形框架ABCD 以匀角速度02ω绕BC 轴转动,正方形框架以匀角速度0ω绕AB 轴转动,如图4所示。