北航理论力学复习

北京航空航天⼤学理论⼒学期末模拟试卷2.pdf理论⼒学AII 期末考试模拟试题⼀、选择题（将正确答案的字母填在空格内，每⼩题2分，共10分）1、对于具有定常约束的质点系，其动能T 最⼀般的形式可以表⽰成的函数。

A ：⼴义速度； B ：⼴义坐标； C: 时间t2、定点运动的圆锥ABC 在⽔平固定圆盘上纯滚动，如图1所⽰。

若圆锥底⾯圆⼼D 作匀速圆周运动，则该圆锥的⾓加速度⽮量α与⾓速度⽮量ω的关系是。

A ：α平⾏于ω；B ：α垂直于ω；C ：为零⽮量α；D ：为⾮零⽮量α图13、⼆⾃由度线性系统的振动周期与有关。

A ：⼴义质量；B ：⼴义刚度；C ：初始位置；D ：初始速度4、只应⽤第⼆类拉格朗⽇⽅程求出⾮⾃由质点系的约束⼒。

A ：⼀定能； B ：⼀定不能； C ：不⼀定能5、第⼆类拉格朗⽇⽅程可⽤于研究具有质点系的⼒学问题。

A ：完整约束； B ：定常约束； C ：⾮完整约束； D ：⾮定常约束注：第⼆类拉格朗⽇⽅程为：),,2,1(d d k j Q q T q T t j j j " ==。

其中k 为系统的⾃由度。

为对应于⼴义坐标的主动⼒的⼴义⼒。

j Q j q ⼆、填空题（将最简结果填在空格内，每空5分，共50分）1、质量为m 的质点M 可在半径为R 的圆环内运动，圆环以⾓速度ω（常⽮量）绕AB 轴作定轴转动，如图2所⽰。

θ为质点的⼴义坐标，此时质点的动能可以表⽰成，其中012T T T T ++=)2,1,0(=i Ti g为⼴义速度的i 次齐次函数。

求：=2T =1T=0T图2 图32、长为L 质量为m 的均质杆OA ⽤光滑柱铰链悬挂在天花板上，下端与刚度系数为k 的⽔平弹簧连接，杆铅垂时弹簧为原长，如图3所⽰。

求系统在平衡位置附近作微幅摆动的动⼒学⽅程。

动⼒学⽅程：。

3、圆盘相对正⽅形框架ABCD 以匀⾓速度02ω绕BC 轴转动，正⽅形框架以匀⾓速度0ω绕AB 轴转动，如图4所⽰。

951力学基础考试大纲(2015版)注意：总分150分，理论力学部分占40%，材料力学部分占60%。

第一部分理论力学大纲静力学1、几何静力学（第1－3章）基本内容：静力学的基本公理，受力分析，力系简化的基本方法和有关力学量的基本计算，平衡方程的建立与求解，摩擦（滑动摩擦和滚动摩擦）问题，桁架内力的计算，平衡结构的静定性问题。

基本要求：深入理解静力学中有关的公理，熟练掌握刚体（刚体系）的受力分析，力系简化的基本方法和有关基本概念和基本量的计算，能够确定给定力系作用下独立平衡方程的数目，能够用定性和定量的方法研究刚体（刚体系）的平衡问题。

能够分析研究考虑摩擦时刚体或刚体系的平衡问题以及平面桁架的内力计算问题。

2、分析静力学（第4章）基本内容：各种力（重力、弹性力、有势力、摩擦力、合力、等效力系）的功，约束及其分类、广义坐标和自由度、虚位移与虚功、理想约束、虚位移原理及其应用、有势力作用下质点系平衡位置的稳定性。

基本要求：熟练计算各种力的功，能够确定系统的约束类型，确定系统的自由度和广义坐标，理解虚位移的基本概念，会判断约束是否是理想约束；能够熟练应用虚位移原理求解质点系平衡问题；会判断有势力作用下质点系平衡位置的稳定性。

动力学1、质点动力学（第五章）基本内容：质点的运动方程、速度、加速度的各种表示方法（矢量法、直角坐标法、自然坐标法）以及有关基本量的计算，质点运动微分方程，点的复合运动（三种运动分析、速度合成定理和加速度合成定理），质点相对运动动力学基本方程。

基本要求：熟练掌握质点运动方程、速度和加速度的各种表示方法和有关基本量的计算，能够熟练建立质点运动微分方程，对于简单的运动微分方程能够求解。

熟练应用点的复合运动的基本理论与方法研究点的复合运动（速度和加速度）问题，能够在非惯性参考系下建立质点相对运动动力学基本方程，具有对质点的运动学和动力学问题进行定性和定量分析的初步能力。

2、质点系动力学（第六章）基本内容：质点系的动量定理、变质量质点动力学方程、动量矩定理（包括对固定点、动点和质心的动量矩定理）、动能定理及其有关基本量的计算。

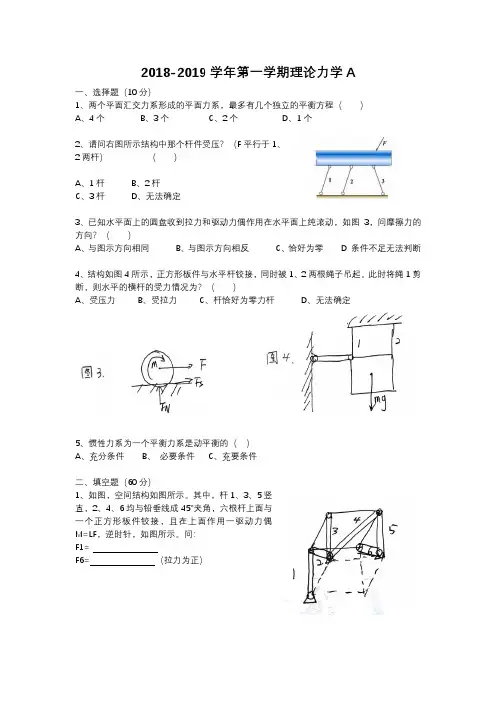
2018-2019学年第一学期理论力学A一、选择题（10分）1、两个平面汇交力系形成的平面力系，最多有几个独立的平衡方程（）A、4个B、3个C、2个D、1个2、请问右图所示结构中那个杆件受压？（F平行于1、2两杆）（）A、1杆B、2杆C、3杆D、无法确定3、已知水平面上的圆盘收到拉力和驱动力偶作用在水平面上纯滚动，如图3，问摩擦力的方向？（）A、与图示方向相同B、与图示方向相反C、恰好为零 D 条件不足无法判断4、结构如图4所示，正方形板件与水平杆铰接，同时被1、2两根绳子吊起。

此时将绳1剪断，则水平的横杆的受力情况为？（）A、受压力B、受拉力C、杆恰好为零力杆D、无法确定5、惯性力系为一个平衡力系是动平衡的（）A、充分条件B、必要条件C、充要条件二、填空题（60分）1、如图，空间结构如图所示。

其中，杆1、3、5竖直，2、4、6均与铅垂线成45°夹角，六根杆上面与一个正方形板件铰接，且在上面作用一驱动力偶M=LF，逆时针，如图所示。

问：F1=F6= （拉力为正）2、在右图所示的机构中，左侧的物体重力为W，在右侧杆上作用一驱动力偶M=aW。

求弹簧弹力大小F=3、如图所示，直角曲杆ACB上套有一圆环M,圆环同时连接一个两端固定的水平直杆，曲杆ACB以如图所示的角速度绕A轴转动，图示位置AC与水平杆夹角为45°，求牵连速度Ve=科氏加速度a c=4、如图，杆OA长为2r，以角速度ω逆时针转动，角加速度为0，通过长为2r的杆AB与一圆盘铰接。

圆盘半径为r，在曲率半径为R=2r的轨道内纯滚动。

当运动位于图示位置时，求圆盘B的角速度w B=圆盘B的角加速度ɑB=杆AB的角加速度ɑAB=5、如图，用两根对称的绳子将质量为m，长为L的杆AB水平吊起，两绳均与AB杆成45°角。

当剪断绳1时，求：AB的角加速度ɑAB=绳2中的张力F=6、如图所示，杆AB长L，质量为m；BC长为L（右边的杆），质量为2m；运动的角速度如图所示，求该结构的动量P=对A轴的动量矩L=三、计算题（30分）半径为R、质量m2=2m的均质圆盘的中心通过柱铰链与长为L、质量为m1=m的均质杆AB连接，杆的A端通过销钉与一个质量忽略不计的物块连接并在光滑水平滑道内运动，圆盘在水平地面上纯滚动，杆与水平地面的夹角为θ。

北航2021年第二学期理论力学复习题北航2021年第二学期理论力学复习题《理论力学》课程学习练习题及参考解答一、填空题1.在介质中上抛一质量为m的小球，已知小球所受阻力r??kv，若选择坐标轴x铅直向上，则小球的运动微分方程为_____________________。

2.质点在运动过程中，在以下条件下，各并作何种运动？①at?0，an?0（请问）：；②at?0，an?0（请问）：；③at?0，an?0（请问）：；④at?0，an?0（请问）：。

3.质量为10kg的质点，受水平力f的作用，在光滑水平面上运动，设f?3?4t（t以s 计，f以n计），初瞬间（t?0）质点位于坐标原点，且其初速度为零。

则t?3s时，质点的位移等于_______________，速度等于_______________。

4.在平面极坐标系中，质点的径向加速度为__________；纵向加速度为_______。

5.哈密顿正则方程用泊松括号则表示为，。

6.质量m?2kg的重物m，摆在长l?0.5m的细绳下端，重物受水平冲击后赢得了速度v0?5m?s?1，则此时绳子的拉力等同于。

7.平面自然坐标系中的切向加速度为，法向加速度为。

8.如果fv，则力所作的功与毫无关系，只与的边线有关。

9.在南半球地面附近自南向北的气流有朝的偏向；而北半球的河流岸冲刷较为严重。

10.未知力的表达式为fx?axy，则该力作功与路径_（填上fy??az，fz??ax。

“有关”或“毫无关系”），该力_保守力（填上“就是”或“不是”）。

11.一质量组由质量分别为m0、2m0、3m0的三个质点组成，某时刻它们的位矢和速22度分别为r1?i?j、v1?2i、r2?j?k、v2?i、r3?k、v3?i?j?k。

则该时刻质点组相对于坐标原点的动量等于，相对于座标原点的动量矩等同于_。

12.一光滑水平直管中有一质量为m的小球，直管以恒定角速度?绕通过管子一端的竖直轴转动，若某一时刻，小球zoyapvxm1到达距o点的距离为a的p点，取x轴沿管，y轴竖直向上，并垂直于管，z轴水平向前，并于管面垂直，如图所示，此时小球相对于管子的速度为v，则惯性离心力大小为，方向为，科里奥利力大小为，方向为。

951力学基础考试大纲注意：总分150分，理论力学部分占40%，材料力学部分占60%。

第一部分理论力学大纲静力学1、几何静力学（第1－3章）基本内容：静力学的基本公理，受力分析，力系简化的基本方法和有关力学量的基本计算，平衡方程的建立与求解，摩擦（滑动摩擦和滚动摩擦）问题，桁架内力的计算，平衡结构的静定性问题。

基本要求：深入理解静力学中有关的公理，熟练掌握刚体（刚体系）的受力分析，力系简化的基本方法和有关基本概念和基本量的计算，能够确定给定力系作用下独立平衡方程的数目，能够用定性和定量的方法研究刚体（刚体系）的平衡问题。

能够分析研究考虑摩擦时刚体或刚体系的平衡问题以及平面桁架的内力计算问题。

2、分析静力学（第4章）基本内容：各种力（重力、弹性力、有势力、摩擦力、合力、等效力系）的功，约束及其分类、广义坐标和自由度、虚位移与虚功、理想约束、虚位移原理及其应用、有势力作用下质点系平衡位置的稳定性。

基本要求：熟练计算各种力的功，能够确定系统的约束类型，确定系统的自由度和广义坐标，理解虚位移的基本概念，会判断约束是否是理想约束；能够熟练应用虚位移原理求解质点系平衡问题；会判断有势力作用下质点系平衡位置的稳定性。

动力学1、质点动力学（第五章）基本内容：质点的运动方程、速度、加速度的各种表示方法（矢量法、直角坐标法、自然坐标法）以及有关基本量的计算，质点运动微分方程，点的复合运动（三种运动分析、速度合成定理和加速度合成定理），质点相对运动动力学基本方程。

基本要求：熟练掌握质点运动方程、速度和加速度的各种表示方法和有关基本量的计算，能够熟练建立质点运动微分方程，对于简单的运动微分方程能够求解。

熟练应用点的复合运动的基本理论与方法研究点的复合运动（速度和加速度）问题，能够在非惯性参考系下建立质点相对运动动力学基本方程，具有对质点的运动学和动力学问题进行定性和定量分析的初步能力。

2、质点系动力学（第六章）基本内容：质点系的动量定理、变质量质点动力学方程、动量矩定理（包括对固定点、动点和质心的动量矩定理）、动能定理及其有关基本量的计算。

理论力学AII 期末考试模拟试题一、 选择题（将正确答案的字母填在空格内，每小题2分，共10分）1、对于具有定常约束的质点系，其动能T 最一般的形式可以表示成 的函数。

A ：广义速度； B ：广义坐标； C: 时间t2、定点运动的圆锥ABC 在水平固定圆盘上纯滚动，如图1所示。

若圆锥底面圆心D 作匀速圆周运动，则该圆锥的角加速度矢量α与角速度矢量ω的关系是 。

A ：α平行于ω；B ：α垂直于ω；C ：为零矢量α；D ：为非零矢量α图13、二自由度线性系统的振动周期与 有关。

A ：广义质量；B ：广义刚度；C ：初始位置；D ：初始速度4、只应用第二类拉格朗日方程 求出非自由质点系的约束力。

A ：一定能； B ：一定不能； C ：不一定能5、第二类拉格朗日方程可用于研究具有 质点系的力学问题。

A ：完整约束； B ：定常约束； C ：非完整约束； D ：非定常约束 注：第二类拉格朗日方程为：),,2,1(d d k j Q q T q T t j j j " ==⎟⎟⎠⎞⎜⎜⎝⎛∂∂−⎟⎟⎠⎞⎜⎜⎝⎛∂∂。

其中k 为系统的自由度。

为对应于广义坐标的主动力的广义力。

j Q j q 二、 填空题（将最简结果填在空格内，每空5分，共50分）1、 质量为m 的质点M 可在半径为R 的圆环内运动，圆环以角速度ω（常矢量）绕AB 轴作定轴转动，如图2所示。

θ为质点的广义坐标，此时质点的动能可以表示成，其中012T T T T ++=)2,1,0(=i Ti g为广义速度的i 次齐次函数。

求：=2T =1T=0T图2 图32、长为L 质量为m 的均质杆OA 用光滑柱铰链悬挂在天花板上，下端与刚度系数为k 的水平弹簧连接，杆铅垂时弹簧为原长，如图3所示。

求系统在平衡位置附近作微幅摆动的动力学方程。

动力学方程： 。

3、圆盘相对正方形框架ABCD 以匀角速度02ω绕BC 轴转动，正方形框架以匀角速度0ω绕AB 轴转动，如图4所示。