物理化学讲稿多组分系统热力学及其在溶液中的应用(10学时)【模板】
- 格式:docx
- 大小:496.60 KB
- 文档页数:24
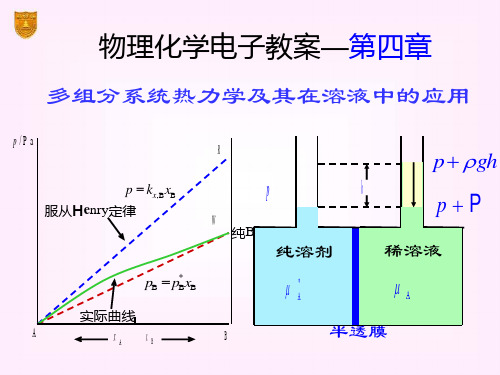

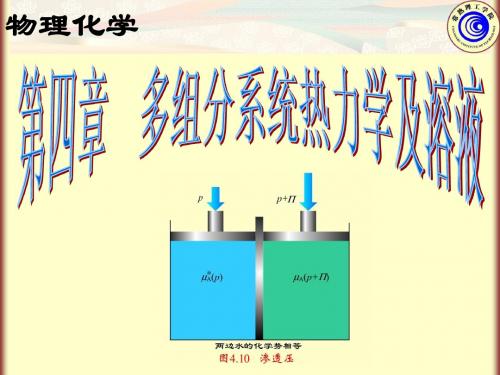

第四章多组分系统热力学及其在溶液中的应用教材分析:本章介绍了溶液组成的表示方法,讲述了化学势和偏摩尔量两个重要概念,将多组分系统的热力学理论应用于溶液中各组分的化学势的表示,从而为研究溶液的各种性质奠定了基础,在此基础上,讨论了稀溶液的最基本的性质——依数性。
它是热力学理论对于溶液系统的应用。
教学目的和要求:通过本章的教学使学生了解和掌握溶液的浓度的各种表示方法,拉乌尔定律及亨利定律,稀溶液、理想溶液的意义;实际溶液与理想溶液的区别;活度的概念及意义,标准态的选用。
化学势及偏摩尔量的定义及相关公式。
掌握稀溶液与理想溶液、非理想溶液三者的区别、关系及各自性质。
加深对拉乌尔定律及亨利定律的理解并熟悉其应用。
活度的概念及标准态的选用及溶液中各组分化学势的表示,是本章的一个难点,必须使学生理解这些概念及其意义。
重点和难点:拉乌尔定律和亨利定律;偏摩尔量和化学势概念;由两个经验定律导出溶液中各组分的化学势的过程和思路;稀溶液、理想溶液的意义;活度的概念与意义;标准态的选用。
教学内容与过程:溶液组成的表示法,偏摩尔量和化学势的概念,溶液的基本性质和两个经验定律,混合气体中各组分的化学势,稀溶液(组分的化学势与标准态,依数性),理想溶液(理想溶液的定义,化学势,通性等)。
思考题、作业:1.课后全部复习题2.作业题:6,8,10,11,12,15,17,18,20,23,25,26,27。
参考资料:1.胡英主编,《物理化学》2.天津大学主编,《物理化学》3.万洪文主编,《物理化学》4.各种习题解题辅导书5.课后所列各种参考读物。
第三节 多组分系统中物质的偏摩尔量与化学势在这以前人们所讨论的热力学体系都是纯组分的体系或者是组分不变的单相体系。
因此,所有的热力学函数U m 、H m 、S m 、G m 、F m 在体系的T 、p 一定的条件下有确定值。
即在这种情况下,要描述体系的状态只要两个状态性质(如T 、p )就行了。

多组分系统热力学及其在溶液中的应用(10学时)物理化学教研室2011 年3 月第一讲 :溶液概述、偏摩尔量和化学势【本讲重点】1、 多组分系统组成的表示及其相互关系;2、 偏摩尔量和化学势的定义,二者的区别和在多相组分系统中引入两种概念的意义。
【本讲难点】偏摩尔量与化学势的概念 【授课方法】讲授【教学手段】多媒体教学与黑板讲述相结合 【计划课时】24.1 引言一、溶液的定义 广义定义:广义地说,两种或两种以上物质彼此以分子或离子状态均匀混合所形成的体系称为溶液。
二、溶液的分类1、按溶液以物态:可分为气态溶液、固态溶液和液态溶液。
2、根据溶液中溶质的导电性:可分为电解质溶液和非电解质溶液。
本章主要讨论液态的非电解质溶液。
三、溶剂和溶质液态溶液:如果都是液态,则把含量多的一种称为溶剂,含量少的称为溶质。
非液态溶液:如果组成溶液的物质有不同的状态,通常将液态物质称为溶剂,气态或固态物质称为溶质。
四、混合物混合物(理想溶液):多组分均匀体系中,溶剂和溶质不加区分,各组分均可选用相同的标准态,使用相同的经验定律,这种体系称为混合物,也可分为气态混合物、液态混合物和固态混合物。
4.2溶液组成的表示法在液态的非电解质溶液中,溶质B 的浓度表示法主要有如下四种: 1.物质B 的质量浓度BB def/m V ρ溶质B 的质量与混合物总体积之比称为溶质B 的物质的量分数,单位为: 3kg m - 。
2.物质的量浓度cBBdefB n c V溶质B 的物质的量与溶液体积V 的比值称为溶质B 的物质的量浓度,或称为溶质B 的浓度,单位是mol/m 3,但常用单位是mol/L 。
3.物质的量分数B BAdefAn x n ∑溶质B 的物质的量与溶液中总的物质的量之比称为溶质B 的物质的量分数,又称为摩尔分数,单位为1。
4.质量摩尔浓度BBAdef n m m溶质B 的物质的量与溶剂A 的质量之比称为溶质B 的质量摩尔浓度,单位是mol/kg 。

第四章 多组分系统热力学及其在溶液中的应用1.在298K 时,有0.10kg 质量分数为0.0947的硫酸H 2SO 4水溶液,试分别用(1)质量摩尔浓度B m ;(2)物质的量浓度和B c (3)摩尔分数B x 来表示硫酸的含量。
已知在该条件下,硫酸溶液的密度为331.060310kg m -⨯⋅ ,纯水的浓度为3997.1kg m -⋅ 。
解:质量摩尔浓度:()2410.19.47%/1009.47%0.1981.067mol H SO B n m W kg -⨯==-⨯=⋅水物质量浓度:()24331009.47%0.10.19.47%/98997.11.02310mol H SO B n c V m --⨯⨯===⨯g 水 摩尔分数:242420.0189H SO B H SO H On x n n ==+2、在K 298和大气压力下,含甲醇()B 的摩尔分数B x 为0.458的水溶液密度为30.8946kg dm -⋅,甲醇的偏摩尔体积313()39.80V CH OH cm mol -=⋅,试求该水溶液中水的摩尔体积2()V H O 。
解:3322CH OH CH OH H O H O V n V n V =+3322CH OH CH OHH O H OV n V V n -=以1mol 甲醇水溶液为基准,则330.45832(10.458)180.027290.894610m V dm ρ⨯+-⨯===⨯ ∴23310.027290.45839.801016.7210.458H OV cm mol ---⨯⨯==⋅-3.在298K 和大气压下,某酒窖中存在酒10.0m3,其中含乙醇的质量分数为0.96。
今欲加水调制含乙醇的质量分数为0.56的酒,试计算(1)应加入水的体积;(2)加水后,能得到含乙醇的质量分数为0.56的酒的体积已知该条件下,纯水的密度为3997.1kg m -⋅,水和乙醇的偏摩尔体积为()25C H OH ω()()6312/10V H O m mol --⋅ ()()63125/10V C H OH m mol --⋅0.96 14.61 58.0 0.5617.11 56.58解:设加入水的物质的量为O H n 2',根据题意,未加水时,2520.9610.96::9.3914618C H OH H O n n -== 2525221C H O H C H O H H O H OV n V n V =⋅+⋅ 即 661001.581061.1410522--⨯⨯+⨯⨯=O H H C O H n n 解出:25167882C H OH n mol =217877H O n mol = 加入水后,25220.5610.56:():0.4984618C H O HH O H On n n -'+== 20.5610.56167882:(17877):0.4984618H O n -'+== 2'317887H O n mol = 加入水的物质的体积为23331788718105.727()999.1H O V m -⨯⨯'== 2525222252'26'6()56.5810(17877)17.1110C H OH C H OH H O H OH OC H OH H OV n V n n V n n--=++=⨯⨯++⨯⨯329.4984495 5.76753115.266V m =+=4.在K 298和kPa 100下,甲醇)(B 的摩尔分数B x 为30.0的水溶液中,水)(A 和甲醇)(B 的偏摩尔体积分别为:132765.17)(-⋅=mol cm O H V ,133632.38)(-⋅=mol cm OH CH V 。
(10学时)物理化学教研室2011 年3 月第一讲:溶液概述、偏摩尔量和化学势【本讲重点】1、多组分系统组成的表示及其相互关系;2、偏摩尔量和化学势的定义,二者的区别和在多相组分系统中引入两种概念的意义。
【本讲难点】偏摩尔量与化学势的概念【授课方法】讲授【教学手段】多媒体教学与黑板讲述相结合 【计划课时】24.1 引言一、溶液的定义 广义定义:广义地说,两种或两种以上物质彼此以分子或离子状态均匀混合所形成的体系称为溶液。
二、溶液的分类1、按溶液以物态:可分为气态溶液、固态溶液和液态溶液。
2、根据溶液中溶质的导电性:可分为电解质溶液和非电解质溶液。
本章主要讨论液态的非电解质溶液。
三、溶剂和溶质液态溶液:如果都是液态,则把含量多的一种称为溶剂,含量少的称为溶质。
非液态溶液:如果组成溶液的物质有不同的状态,通常将液态物质称为溶剂,气态或固态物质称为溶质。
四、混合物混合物(理想溶液):多组分均匀体系中,溶剂和溶质不加区分,各组分均可选用相同的标准态,使用相同的经验定律,这种体系称为混合物,也可分为气态混合物、液态混合物和固态混合物。
4.2溶液组成的表示法在液态的非电解质溶液中,溶质B 的浓度表示法主要有如下四种: 1.物质B 的质量浓度B B def/m V ρ溶质B 的质量与混合物总体积之比称为溶质B 的物质的量分数,单位为: 3kg m - 。
2.物质的量浓度cB BdefBn c V溶质B 的物质的量与溶液体积V 的比值称为溶质B 的物质的量浓度,或称为溶质B 的浓度,单位是mol/m 3,但常用单位是mol/L 。
3.物质的量分数B BAdefAn x n ∑溶质B 的物质的量与溶液中总的物质的量之比称为溶质B 的物质的量分数,又称为摩尔分数,单位为1。
4.质量摩尔浓度BBAdef n m m溶质B 的物质的量与溶剂A 的质量之比称为溶质B 的质量摩尔浓度,单位是mol/kg 。
5.质量分数 BB ()m w m =总溶质B 的质量与溶液总质量之比称为溶质B 的质量分数,单位为1。
[练习]试推导在无限稀释的水溶液中:B AB B A c M x m M ρ==4.3-4.4 偏摩尔量化学势一、 单组分体系的摩尔热力学函数值体系的状态函数中V ,U ,H ,S ,A ,G 等是广度性质,与物质的量有关。
设由物质B 组成的单组分体系的物质的量为 B n ,则各摩尔热力学函数(摩尔体积、摩尔热力学能、摩尔焓、摩尔熵、摩尔亥姆赫兹自由能、摩尔吉布斯自由能)值的定义式分别为:*m,B B V V n =*m,B B U U n = *m,B B H H n = *m,B B S S n = *m,B B A A n = *m,B BG G n =各摩尔热力学函数都是强度性质。
二、多组分体系(内部组成可变)的摩尔热力学函数值多组分体系中,每个热力学函数的变量就不止两个,还与组成体系各物的物质的量有关。
[例子]一定量的乙醇溶解于水中,形成溶液。
252525C *m,C C H OH H OHH OHV V n = 222*m,H O H O H OV V n =**22225H O H O H O C H OH V n V n V ≠+溶液即:1mol 乙醇加入溶液中时,引起溶液体积的变化不等于乙醇的摩尔体积。
同理:**22225H O H O H O C H OH U n U n U ≠+溶液二、偏摩尔量的定义1、定义 设Z 代表V ,U ,H ,S ,A ,G 等广度性质,则对多组分体系12k (,,,,,)Z fT p n n n =偏摩尔量Z B Z B :称为物质B 的某种容量性质Z 的偏摩尔量。
2、物理意义:等温、等压条件下,在系统中加入1molB 物质,所引起的系统某一广度性质的改变量,对上例:222525H O H O C H OH C H OH V n V n V =+溶液3、注意:A.偏摩尔量的含义是:在等温、等压、保持B 物质以外的所有组分的物质的量不变的条件下,改变 所引起广度性质Z 的变化值,或在等温、等压条件下,在大量的定组成体系中加入1molB 物质所引起广度性质Z 的变化值。
B.只有广度性质才有偏摩尔量,而偏摩尔量是强度性质。
C.纯物质的偏摩尔量就是它的摩尔量。
D.任何偏摩尔量都是T ,p 和组成的函数。
三、偏摩尔量的集合(加和)公式设一个均相体系由1、2、 、k 个组分组成,则体系任一容量性质Z 应是T ,p 及各组分物质的量的函数,即:12k (,,,,,)Z Z T p n n n =⋅⋅⋅在等温、等压条件下:2k 13k 1k-1,,,,1,,,,,2,,,,k 12k ()d ()d +d ()d T p n n T p n n n T p n n Z Z Zn n n n n n Z ⋅⋅⋅⋅⋅⋅⋅⋅⋅∂∂∂=+⋅⋅⋅+∂∂∂k,,(B)B=1B=()c T p n c Z n ≠∂∂∑ 按偏摩尔量定义:c B ,,(B)B()T p n c ZZ n ≠∂=∂ 则 1122k k BB 1d d d d d kn Z Z n Z n Z n Zn ==++⋅⋅⋅+=∑在保持偏摩尔量不变的情况下,对上式积分:12k1122k k 0d d d n n n Z Z n Z n Z n =++⋅⋅⋅+⎰⎰⎰1122k k Z n Z n Z n Z =++⋅⋅⋅+kB B B=1=n Z ∑这就是偏摩尔量的集合公式,说明体系的总的容量性质等于各组分偏摩尔量的加和。
例:二组分系统,各组分的物质量和的偏摩尔体积分别为:11,n V 和22,n V ,则 总体积:1122V nV n V =+ 写成一般式有:c B B B ,,(B)BB ()T p n c SS n S S n ≠∂==∂∑c B B B ,,(B)BB()T p n c UU n U U n ≠∂==∂∑c B B B ,,(B)BB()T p n c HH n H H n ≠∂==∂∑c B B B ,,(B)BB ()T p n c GG n G G n ≠∂==∂∑c B B B ,,(B)BB()T p n c AA n A A n ≠∂==∂∑ 四、Gibbs-Duhem 公式---偏摩尔量之间的关系 如果在溶液中不按比例地添加各组分,则溶液浓度会发生改变,这时各组分的物质的量和偏摩尔量均会改变。
根据加和公式 1122k k Z n Z n Z n Z =++⋅⋅⋅+对Z 进行微分111122223333d d d d d d d Z n Z Z n n Z Z n n Z Z n =+++()+()+()k k k k d d n Z Z n +⋅⋅⋅++ 1122k k 1122k k d d d +dZ d ddZ Z n Z n Z n n Z n Z ∴=++⋅⋅⋅+++⋅⋅⋅+()(n )11+-----1k kB B B B B B Z dn n dZ ===∑∑()在等温、等压下某均相体系任一容量性质的全微分为:()1122k k 1d d d d = ----2kB B B Z Z n Z n Z n Z dn ==++⋅⋅⋅+∑()1122k k 1d d d ==0 ----3kB B B n Z n Z n Z n dZ =++⋅⋅⋅+∑比较两式:1122k k d d d 0or x Z x Z x Z ++⋅⋅⋅+=1122k k d d d 0n Z n Z n Z ++⋅⋅⋅+=k B B B=1d 0n Z =∑即 kB B B=1d 0or x Z =∑这就称为Gibbs-Duhem 公式,说明偏摩尔量之间是具有一定联系的。
表明:在温度、压强一定时,若溶液发生一状态变化,必然有一些组分的偏摩尔量增加,一些组分的偏摩尔量减小,所有组分的物质的量与其偏摩尔量乘积之和为0。
五、化学势的定义 (一)化学势的定义:设:某系统中有1,2….k 种物质,则: ...k U U S V n n n =(,,,),,()()B C B C V n n S n n B B U U dU dS dV S V ∂∂∴=+∂∂,,1212()()......()CCCS V n S V n S V n k k U U U dn dn dn n n n ⎡⎤∂∂∂+++⎢⎥∂∂∂⎣⎦,,,,,, ,,1,()()B C B C CkV n n S n n B B B S V nU UU dU dS dV dn S V n =⎛⎫∂∂∂=++ ⎪∂∂∂⎝⎭∑,,, B ,,(c B)()c S V n BUn μ≠∂=∂令---称为物质B的化学势,,1()()B C B C kV n n S n n B B B U UdU dS dV dn S V μ=∂∂∴=++∂∂∑,,对组成不变的系统:,B V n U T S ∂⎛⎫=⎪∂⎝⎭ ,BS n U p V ∂⎛⎫=- ⎪∂⎝⎭ 11B B B dU TdS pdV dn μ==-+----∑()因:H=U+pV ,则 12BB B dH TdS Vdp dn μ==++---∑()A=U-TS ,则 13BBB dA SdT Vdp dnμ==-++---∑()G=H-TS ,则 14B B B dG SdT Vdp dn μ==++---∑()-----组成可变系统的热力学基本公式 1、化学势的广义定义:由(1)~(4)有B ,,,,,,,,()()()()c c c c S V n S p n T V n T p n B B B BU H A Gn n n n μ∂∂∂∂====∂∂∂∂ 化学势的狭义定义:B ,,()c T p n BGn μ∂=∂ 注意:若不做说明,化学势指偏摩尔Gibbs 自由能。
保持温度、压力和除B 以外的其它组分不变,体系的Gibbs 自由能随B n 的变化率称为化学势,所以化学势就是偏摩尔Gibbs 自由能。
(二)化学势判据化学势在热力学中具有重要的作用,是确定系统平衡与自发变化的重要参量,若系统不做非体积功,则10kBB B dnμ=⎧⎨⎩∑:自发过程=0:可逆过程或系统处于平衡状态(三)化学势在相平衡中的应用βα→ B B dn dn αβ=-发生相转移的条件:()0T p dG ≤,B B B B dG dG dG dn dn αβααββμμ=+=+()0B B B dG dn αβαμμ=-≤ B B βαμμ∴≥结论:化学势是决定物质传递方向的强度变量。
六、化学势温度、压力的关系 (一)化学势与温度的关系c c c B c ,,,,,,,B ()[()]B T p n n T p n T n n Gp p n μ∂∂∂=∂∂∂Bcc,,,,B [()]T n n T p n G n p ∂∂=∂∂c,,B()T p n V n ∂=∂B V =对于纯组分体系,根据基本公式,有:对多组分体系,把 m G 换为B μ,则摩尔体积变为偏摩尔体积B V 。