人教版小学六年级数学计算竞赛竞赛题

人教版六年级上册数学竞赛试题一、PK 擂台赛,我能在括号里填上正确的答案。

（每小题2分，共20分）1. “六（1）班人数是六（2）班人数的76”是把（ ）看作单位“1”，（ ）占（ ）的67。

如果六（2）班有42人，那两个班一共有（ ）人。

2.(())＝（ ）∶（ ）＝140%＝35÷（ ）＝（ ）。

3. 把73米铁丝平均分成3份，每份长（ ）米，第二份占全长的(())。

4. 全世界有200来个国家，其中缺水的国家有100多个，严重缺水的国家有40多个。

缺水的国家约占全世界国家总数的（ ）％，严重缺水的国家约占全世界国家总数的（ ）％。

5. 某饭店十月份的营业额是30万元，如果按营业额的5%缴纳营业税，该饭店十月份应缴纳营业税( )元。

6、直径为10分米的半圆，周长是（ ）分米。

7. 80%的倒数是（ ），132的倒数是（ ）。

8. 在100克水中加入25克盐，那么盐水的含盐率是（ ）。

9. 85∶0.125的比值是（ ），化成最简整数比是（ ）。

10. 把一个正方体切成两个小长方体，正方体表面积是两个长方体表面积总和的(())。

二、我是公正小法官,能准确判断是与非。

（对的打“√”，错的打“×”。

5分）11. 4∶5的后项增加10，要使比值不变，前项应增加8。

（ ） 12. 在32、0.67、66.7%中最大的数是66.7%。

（ ） 13. 一个数除以分数的商一定比原来的数大。

（ ）14. 定价100元的商品，先提价20%，再降价20%，还是原价。

（ ） 15. 甲数除以乙数，等于甲数乘乙数的倒数。

（ ） 三、快乐ABC,我选得又快又准。

（每小题2分，共10分） 16. 下列图形中，对称轴最少的是（ ）A 、长方形B 、正方形C 、等腰三角形D 、圆 17. 一个圆的半径扩大4倍，面积扩大( )倍。

A 、4B 、8C 、16D 、 ∏18. 一根长2米的绳子，先用去31，再用去31米，还剩下（ ）米。

2020-2021学年人教版六年级下学期数学竞赛试卷
一、填空题
1．我们常用的数是十进制数，计算机程序使用的是二进制数（只有数码0和1）．它们两者可以相互换算，如将二进制数（101）2改成十进制数：（101）2＝1×22+0×21+1×20＝4+0+1＝5．
（1）将二进制数（10101）2换成十进制数是．
（
2）将十进制数13换成二进制数是．
2．将下列十进制数改写成二进制数
（1）（106）10＝2
（2）（19）10＝2
（3）（987）10＝2
（4）（1993）10＝2．
3．把下列十进制数化成二进制数：
（1）139（10）＝．
（2）312（10）＝．
（3）477（10）＝．
4．将6个灯泡排成一行，用○和●表示灯亮和灯不亮，如图是这一行灯的五种情况，分别表示五个数字：1，2，3，4，5．那么○●●○●○表示的数是．
5．（1010101.1011）2＝10．
6．日常生活中经常使用十进制来表示数，要用10 个数码：0、1、2、3、4、5、6、7、8、9．在电子计算机中用二进制，只要用两个数码0和1．正像在十进制中加法要“逢十进一”，在二进制中必须“逢2进1”，于是，可以得到以下自然数的十进制与二进制表示对照表：
十进制012345678…
二进制0110111001011101111000…
第1 页共20 页。

小学人教版六年级趣味数学竞赛试题图文百度文库一、拓展提优试题1．A、B、C、D四个箱子中分别装有一些小球，现将A箱中的部分小球按如下要求转移到其他三个箱子中：该箱中原有几个小球，就再放入几个小球，此后，按照同样的方法依次把B、C、D箱中的小球转移到其他箱子中，此时，四个箱子都各有16个小球，那么开始时装有小球最多的是箱，其中装有小球个．2．某工程队修建一条铁路隧道，当完成任务的时，工程队采用新设备，使修建速度提高了20%，同时为了保养新设备，每天工作时间缩短为原来的，结果，前后共用185天完工，由以上条件可推知，如果不采用新设备，完工共需天．3．王涛将连续的自然数1，2，3，…逐个相加，一直加到某个自然数为止，由于计算时漏加了一个自然数而得到错误的结果2012．那么，他漏加的自然数是．4．李华在买某一商品的时候，将单价中的某一数字“7”错看成了“1”，准备付款189元，实际应付147元，已知商品的单价及购买的数量都是整数，则这种商品的实际单价是元，李华共买了件．5．如图，已知AB＝40cm，图中的曲线是由半径不同的三种半圆弧平滑连接而成，那么阴影部分的面积是cm2．（π取3.14）6．如图，六边形ABCDEF的周长是16厘米，六个角都是120°，若AB＝BC ＝CD＝3厘米，则EF＝厘米．7．如图是甲乙丙三人单独完成某项工程所需天数的统计图，根据图中信息计算，若甲先做2天，接着乙丙两人合作了4天，最后余下的工程由丙1人完成，则完成这项工程共用天．8．在救灾捐款中，某公司有的人各捐200元，有的人各捐100元，其余人各捐50元．该公司人均捐款元．9．甲挖一条水渠，第一天挖了水渠总长度的，第二天挖了剩下水渠长度的，第三天挖了未挖水渠长度的，第四天挖完剩下的100米水渠．那么，这条水渠长米．10．已知A是B的，B是C的，若A+C＝55，则A＝．11．等腰△ABC中，有两个内角的度数比是1：2，则△ABC的内角中，角度最大可以是度．12．能被5和6整除，并且数字中至少有一个6的三位数有个．13．a，b，c是三个互不相等的自然数，且a+b+c＝48，那么a，b，c的乘积最大是．14．甲、乙两人分别从A、B两地同时出发，相向而行，在C点相遇，若在出发时，甲将速度提高，乙将速度每小时提高10千米，二人依然在C点相遇，则乙原来每小时行千米．15．如图，将1个大长方形分成了9个小长方形，其中位于角上的3个小长方形的面积分别为9，15和12，由第4个角上的小长方形的面积等于．【参考答案】一、拓展提优试题1．解：根据最后四个箱子都各有16个小球，所以小球总数为16×4＝64个，最后一次分配达到的效果是，从D中拿出一些小球，使A、B、C中的小球数翻倍，则最后一次分配前，A、B、C中各有小球16÷2＝8个，由于小球的转移不改变总数，所以最后一次分配前，D中有小球64﹣8﹣8﹣8＝40个；于是得到D被分配前的情况：A8，B8，C8，D40；倒数第二次分配达到的效果是，从C中拿出一些小球，使A、B、D中的小球数翻倍，则倒数第二次分配前，A、B中各有小球8÷2＝4个，D中有40÷2＝20个，总数不变，所以最后一次分配前，C中有小球64﹣4﹣4﹣20＝36个，于是得到C被分配前的情况：A4，B4，C36，D20，同样的道理，在B被分配前，A中有小球4÷2＝2个，C中有小球36÷2＝18个，D中有小球20÷2＝10个，B中有小球64﹣2﹣18﹣10＝34个，即B被分配前的情况：A2，B34，C18，D10；再推导一次，在A被分配前，B中有小球34÷2＝17个，C中有小球18÷2＝9个，D中有小球10÷2＝5个，B中有小球64﹣17﹣9﹣5＝33个，即A被分配前的情况：A33，B17，C9，D5；而A被分配前的情况，就是一开始的情况，所以一开始，A箱子装有最多的小球，数量为33个；答：开始时装有小球最多的是A箱，其中装有33小球个；故答案为：A，33．2．解：设计划用x天完成任务，那么原计划每天的工作效率是，提高后每天的工作效率是×（1+20%）＝×＝，前面完成工程的所用时间是天，提高工作效率后所用的实际是（185﹣）×天，所以，+（185﹣）××＝1，+（185﹣）××﹣＝1﹣，（185﹣）××＝，（185﹣）×÷＝÷，185﹣+＝x+，x÷＝185÷，x＝180，答：工程队原计划180天完成任务．故答案为：180．3．解：设这个等差数列和共有n项，则末项也应为n，这个等差数列的和为：（1+n）n÷2＝；经代入数值试算可知：当n＝62时，数列和＝1953，当n＝63时，数列和＝2016，可得：1953＜2012＜2016，所以这个数列共有63项，少加的数为：2016﹣2012＝4．故答案为：4．4．解：189＝3×3×3×7＝27×7147＝3×7×7＝21×7正好是27×7＝189中把27看成21×7＝147所以这种商品的实际单价是21元，卖了7件．故答案为：21，7．5．解：40÷2＝20（厘米）20÷2＝10（厘米）3.14×202﹣3.14×102÷2×4＝1256﹣628＝628（平方厘米）答：阴影部分的面积是628平方厘米．故答案为：628．6．解：如图延长并反向延长AF，BC，DE，分别相交与点G、H、N，因六边形ABCDEF的每个角是120°所以∠G＝∠H＝∠N＝60°所以△GHN，△GAB，△HCD，△EFN都是等边三角形AB＝BC＝CD＝3厘米，△GHN边长是3+3+3＝9（厘米）AN＝9﹣3＝6（厘米）AN＝AF+EFDE＝六边形ABCDEF的周长﹣AB﹣BC﹣CD﹣（AF+EF）＝16﹣3﹣3﹣3﹣6＝1（厘米）EF＝EN＝9﹣3﹣1＝5（厘米）答：EF＝5厘米．故答案为：5．7．解：依题意可知：甲乙丙的工作效率分别为：，，；甲乙工作总量为：×2+×4＝；丙的工作天数为：（1﹣）＝3（天）；共工作2+4+3＝9故答案为：98．解：捐50元人数的分率为：1﹣＝，（200×+100×+50×）÷1＝（20+75+7.5）÷1＝102.5（元）答：该公司人均捐款102.5元．故答案为：102.5．9．解：把这条水渠总长度看作单位“1”，则第一天挖的分率为，第二天挖的分率（1﹣）×＝，第三天挖的分率为（1﹣）×＝，100÷（（1﹣﹣﹣）＝100÷＝350（米）答：这条水渠长350米．故答案为：350．10．解：A是C的×＝，即A＝C，A+C＝55，则：C+C＝55C＝55C＝55÷C＝40A＝40×＝15故答案为：15．11．解：180°×＝180°×＝90°答：角度最大可以是 90度．故答案为：90．12．解：根据分析，分解质因数6＝2×3∴这个三位数能同时被2、3、5整除，而且数字中至少含有一个6∴这个三位数的个位数必须为偶数或0，因被5整除的数个位数必须是0或5，故个位数为0，设此三位数为，按题意a、b中至少有一个数字为6，①a＝6时，则6+b+0 是3的倍数，则b＝0，3，6，9，符合的三位数为：600、630、660、690②b＝6时，则6+a+0 是3的倍数，则a＝3，6，9，符合的三位数为：360、660、960综上所述，符合题意的三位数为：360、660、960、600、630、690故答案为：6．13．解：48÷3＝16，16﹣1＝15，16+1＝17，所以，a，b，c的乘积最大是：15×16×17＝4080．故答案为：4080．14．解：依题意可知：根据甲乙两人的相遇点相同，那么他们的速度比例是不变的．当甲提高时，乙也同样需要提高，而乙提高的是每小时10千米．即10÷＝40千米/小时．故答案为：4015．解：如图，设D的面积为x，9：12＝15：x9x＝12×15x＝x＝20答：第4个角上的小长方形的面积等于20．故答案为：20．。

人教版六年级上册数学竞赛试题一、擂台赛,我能在括号里填上正确的答案。

〔每题2分，共20分〕 1. “六〔1〕班人数是六〔2〕班人数的76〞是把〔 〕看作单位“1”，〔 〕占〔 〕的67。

假如六〔2〕班有42人，那两个班一共有〔 〕人。

2.(())＝〔 〕∶〔 〕＝140%＝35÷〔 〕＝〔 〕。

3. 把73米铁丝平均分成3份，每份长〔 〕米，第二份占全长的(())。

4. 全世界有200来个国家，其中缺水的国家有100多个，严峻缺水的国家有40多个。

缺水的国家约占全世界国家总数的〔 〕％，严峻缺水的国家约占全世界国家总数的〔 〕％。

5. 某饭店十月份的营业额是30万元，假如按营业额的5%缴纳营业税，该饭店十月份应缴纳营业税( )元。

6、直径为10分米的半圆，周长是〔 〕分米。

7. 80%的倒数是〔 〕，132的倒数是〔 〕。

8. 在100克水中参与25克盐，则盐水的含盐率是〔 〕。

9. 85∶0.125的比值是〔 〕，化成最简整数比是〔 〕。

10. 把一个正方体切成两个小长方体，正方体外表积是两个长方体外表积总和的(())。

二、我是公正小法官,能精确推断是及非。

〔对的打“√〞，错的打“×〞。

5分〕11. 4∶5的后项增加10，要使比值不变，前项应增加8。

〔 〕 12. 在32、0.67、66.7%中最大的数是66.7%。

〔 〕 13. 一个数除以分数的商肯定比原来的数大。

〔 〕 14. 定价100元的商品，先提价20%，再降价20%，还是原价。

〔 〕 15. 甲数除以乙数，等于甲数乘乙数的倒数。

〔 〕 三、欢乐,我选得又快又准。

〔每题2分，共10分〕16. 以下图形中，对称轴最少的是〔 〕A 、长方形B 、正方形C 、等腰三角形D 、圆 17. 一个圆的半径扩大4倍，面积扩大( )倍。

A 、4 B 、8 C 、16 D 、 ∏18. 一根长2米的绳子，先用去31，再用去31米，还剩下〔 〕米。

人教版六年级上学期数学竞赛试题(含答案)一、拓展提优试题1．用底面内半径和高分别是12cm，20cm的空心圆锥和空心圆柱各一个组成如图所示竖放的容器，在这个容器内注入一些细沙，能填满圆锥，还能填部分圆柱，经测量，圆柱部分的沙子高5cm，若将这个容器倒立，则沙子的高度是cm．2．有两辆火车，车长分别是125米和115米，车速分别是22米/秒和18米/秒，两车相向行驶，从两车车头相遇到车尾分开需要秒．3．甲、乙两家商店出售同一款兔宝宝玩具，每只原售价都是25元，为了促销，甲店先提价10%，再降价20%；乙店则直接降价10%．那么，调价后对于这款兔宝宝玩具，店的售价更便宜，便宜元．4．若算式（□+121×3.125）÷121的值约等于3.38，则□中应填入的自然数是．5．图中每一个圆的面积都是1平方厘米，则六瓣花形阴影部分的面积是平方厘米．6．王老师在黑板上写了若干个从1开始的连续自然数：1，2，3，4，…，然后擦去三个数（其中有两个质数），如果剩下的数的平均数是19，那么王老师在黑板上共写了39个数，擦去的两个质数的和最大是．7．小强和小林共有邮票400多张，如果小强给小林一些邮票，小强的邮票就比小林的少；如果小林给小强同样多的邮票，则小林的邮票就比小强的少，那么，小强原有227张邮票，小林原有张邮票．8．如图所示的“鱼”形图案中共有个三角形．9．已知自然数N的个位数字是0，且有8个约数，则N最小是．10．如图，设定E、F分别是△ABC的边AB、AC上的点，线段CE，BF交于点D，若△CDF，△BCD，△BDE的面积分别为3，7，7，则四边形AEDF的面积是．11．如图是甲乙丙三人单独完成某项工程所需天数的统计图，根据图中信息计算，若甲先做2天，接着乙丙两人合作了4天，最后余下的工程由丙1人完成，则完成这项工程共用天．12．从12点整开始，至少经过分钟，时针和分针都与12点整时所在位置的夹角相等．（如图中的∠1＝∠2）．13．如图，已知AB＝2，BG＝3，GE＝4，DE＝5，△BCG和△EFG的面积和是24，△AGF和△CDG的面积和是51．那么，△ABC和△DEF的面积和是．14．甲、乙两人拥有邮票张数的比是5：4，如果甲给乙5张邮票，则甲、乙两人邮票张数的比变成4：5．两人共有邮票张．15．如图，将一根长10米的长方体木块锯成6段，表面积比原来增加了100平方分米，这根长方体木块原来的体积是立方分米．【参考答案】一、拓展提优试题1．解：据分析可知，沙子的高度为：5+20÷3＝11（厘米）；答：沙子的高度为11厘米．故答案为：11．2．解：（125+115）÷（22+18）＝240÷40＝6（秒）；答：从两车头相遇到车尾分开需要6秒钟．故答案为：6．3．解：甲商店：25×（1+10%）×（1﹣20%），＝25×110%×80%，＝27.5×0.8，＝22（元）；乙商店：25×（1﹣10%），＝25×90%，＝22.5（元）；22.5﹣22＝0.5（元）；答：甲商店便宜，便宜了0.5元．故答案为：甲，0.5．4．解：令□＝x，那么：（x+121×3.125）÷121，＝（x+121×3.125）×，＝x+121×3.125×，＝x+3.125；x+3.125≈3.38，x≈0.255，0.255×121＝30.855；x＝30时，x＝×30≈0.248；x＝31时，x＝×31≈0.255；当x＝31时，运算的结果是3.38．故答案为：31．5．解：1×2＝2（平方厘米）；答：六瓣花形阴影部分的面积是2平方厘米．故答案为：2．6．解：由剩下的数的平均数是19，即得最大的数约为20×2＝40个，又知分母是9，所以剩下的数的个数必含因数9，则推得剩余36个数．原写下了1到39这39个数；剩余36个数的和：19×36＝716，39个数的总和：（1+39）×39÷2＝780，擦去的三个数总和：780﹣716＝64，根据题意，推得擦去的三个数中最小是1，那么两个质数和63＝61+2能够成立，61＞39不合题意；如果擦去的另一个数是最小的合数4，64﹣4＝6060＝29+31＝23+37，成立；综上，擦去的两个质数的和最大是60．故答案为：39，60．7．解：（1﹣）：1＝13：19，13+19＝32；1：（1﹣）＝17：11，17+11＝28，32与28的最小公倍数是224，小强和小林共有邮票400多张，所以共有224×2448÷32×13＝182，448÷28×17＝272．小强：（182+272）÷2＝227张小林：448﹣227＝221．故答案为：227，221．8．解：由一个三角形组成：14个；由两个三角形组成：8个；由三个三角形组成：8个；由四个三角形组成：4个；由六个三角形组成：1个；总共：14+8+8+4+1＝35个．故共有35个三角形．故答案为：35．9．解：自然数N的个位数字是0，它一定有质因数5和2，要使N最小，5的个数应最少为1个，而求其它因数最好都是2和3，并且2的个数不能超过2个，其它最好都是3；设这个自然数N＝21×51×3a，根据约数和定理，可得：（a+1）×（1+1）×（1+1）＝8，（a+1）×2×2＝8，a＝1；所以，N最小是：2×3×5＝30；答：N最小是30．故答案为：30．10．解：连接AD，因△CDF和△BCD的高相等，所以FD：DB＝3：7，所△AFD和△ABD的面积比也是3：7，即可把△AFD的面积看作是3份，△ABD的面积看作是7份，S△BCD＝7，S△BDE＝7所以CD＝DE，S△ACD＝S△ADE，S△ACD+S△BDE＝S△ABD，S△ACD+S△BDE＝7份，S△AFD+S△CDF+S△BDE＝7份，3份+3+7＝7份，则1份＝2.5，S四边形AEDF＝10份﹣7＝10×2.5﹣7＝18答：四边形AEDF的面积是18．故答案为：18．11．解：依题意可知：甲乙丙的工作效率分别为：，，；甲乙工作总量为：×2+×4＝；丙的工作天数为：（1﹣）＝3（天）；共工作2+4+3＝9故答案为：912．解：设所走的时间为x小时．30x＝360﹣360x3x+360x＝360﹣30x+360390x＝360x＝小时＝55分钟．故答案为：55．13．解：作CM⊥AD，垂足为M，作FN⊥AD，垂足为N，设CM＝x，FN＝y．由题意得方程组，解方程组得，所以△ABC与△DEF的面积和是：AB•CM+DE•FN＝×2×8+×5×6＝8+15＝23．故答案为：23．14．解：5÷（）＝5＝45（张）答：两人共有邮票 45张．故答案为：45．15．解：依题意可知：将一根长10米的长方体木块锯成6段，表面积比原来增加了100平方分米，变面积增加了10个面，那么每一个面的面积为100÷10＝10平方分米．10米＝100分米．体积为：10×100＝1000（立方分米）．故答案为：1000。

人教版小学六年级数学上册竞赛试卷附答案人教版小学六年级数学上册竞赛试卷附答案人教版小学六年级数学上册竞赛试卷题目（一)一、认真思考，仔细填写。

(2７分)(1)、0．35的倒数是( )。

(2)、在３:8中，把比的前项加上９,要使比值不变，比的后项应加上（）。

(3)、２.５:0.5 化简成最简整数比是(),比值是（)。

(４)、1５:( )＝38 ＝36 ( ）=( ）%=( )（小数)＝()成(5)、一个圆的半径是5ｃm,直径是( ）cｍ，周长是( )cm，面积是( )c㎡。

(6)、六(１)班女生人数是男生人数的2５,男生比女生多( )（) ,女生人数与全班人数的比是( ),男生人数占全班的( ) (）。

（7)、小翔在2０08年到银行存款20０元,按两年期年利率2.79%计算，到２0１0年到期时,利息是()元,利息的税金按5%交纳是( )元，可得到本金和税后利息一共（)元。

(8)、一件５00元的皮衣打折后卖425元,这是打( )折,比原价便宜了（)%。

(9)、一根绳子长57 米，平均分成5份,每份占全长的()，每份长()米。

（10)、如果ａ1１1２＝ｂ1２= c3４(a、b、c不为0),则( )﹥( ）﹥( ）。

(１1)、班主任张老师带领五(２）班50名同学栽树,张老师一人栽5棵,男生一人栽3棵,女生一人栽2棵,总共栽树120棵，男生和女生分别有（)名和()名。

二、仔细推敲,认真辨析。

（对的打，错的打）(５分)(1)比的前项和后项都增加或减少相同的数，比值不变。

( ）（2)如果大圆和小圆的半径比是5：1,面积和周长的比都是25：1。

( )(3）生产105个零件，全部合格,合格率是１00%。

( )（4)甲数比乙数多甲数与乙数的比是1：4。

（）(5)10克盐溶解在100克水中，含盐率10%( )三、反复比较，谨慎选择。

(把正确答案的序号填在括号里）(5分)(1)要想更清楚地了解各部分数量同总数之间的关系,应该选用（)A.条形统计图Ｂ.折线统计图C.扇形统计图(2)在、６6.78%和0.6７这三个数中最大的一个是( ）A. B.66.78% Ｃ.0.６7(3)画圆时,圆的周长为15．７cm，那么圆规两脚间的距离为(）A.２.５ｃmＢ.5cm C.15.7cm（4)王红的体重比李云的体重重，那么李云的体重比王红体重轻( )A．Ｂ. C.(5)一件20元的商品，先提价1５%,再降价15%，这件商品（）A.比原价贵Ｂ．价钱不变C.比原价便宜四、开动脑筋，灵活计算。

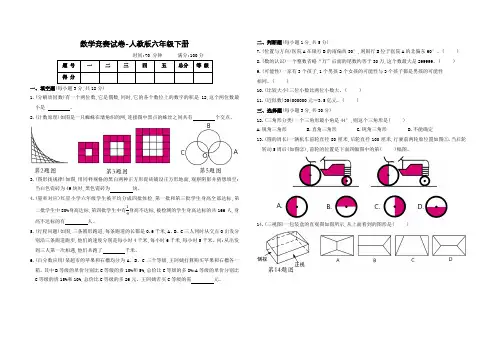
数学竞赛试卷-人教版六年级下册时间:70 分钟满分:100分题号一二三四五总分等级得分一、填空题(每小题3分,共18分)1.(分解质因数)有一个两位数,它是偶数,同时,它的各个数位上的数字的积是12,这个两位数最小是。

2.(计数原理)如图是一只蜘蛛在墙角织的网,连接图中黑点的蛛丝之间共有个交点。

3.(图形找规律)如图,用同样规格的黑白两种正方形瓷砖铺设正方形地面,观察阴影并猜想填空:当白色瓷砖为49块时,黑色瓷砖为块。

4.(量率对应)红星小学六年级学生被平均分成四批体检,第一批和第三批学生身高全部达标,第二批学生中80%身高达标,第四批学生中有19身高不达标,被检测的学生身高达标的共166人,身高不达标的有人。

5.(行程问题)如图,三条圆形跑道,每条跑道的长都是0.6千米,A、B、C三人同时从交点O出发分别沿三条跑道跑步,他们的速度分别是每小时4千米,每小时6千米,每小时5千米。

问:从出发到三人第一次相遇,他们共跑了千米。

6.(百分数应用)某超市的苹果和石榴均分为A、B、C三个等级,王阿姨打算购买苹果和石榴各一箱。

其中B等级的单价分别比C等级的贵10%和5%,总价比C等级的多8%;A等级的单价分别比C等级的贵15%和10%,总价比C等级的多26元。

王阿姨若买C等级的需元。

二、判断题(每小题1分,共5分)7.(位置与方向)医院A在银行B的南偏西30°,则银行B位于医院A的北偏东60°。

( )8.(数的认识)一个整数省略“万”后面的尾数约等于30万,这个数最大是299999。

( )9.(可能性)一家有3个孩子,1个男孩2个女孩的可能性与3个孩子都是男孩的可能性相同。

( )10.(比较大小)三位小数比两位小数大。

( )11.(近似数)354000000元≈3.5亿元。

( )三、选择题(每小题3分,共30分)12.(三角形分类)一个三角形最小角是44°,则这个三角形是( )A.锐角三角形B.直角三角形C.钝角三角形D.不能确定13.(圆的周长)一辆机车前轮直径80厘米,后轮直径100厘米,行驶前两轮胎位置如图①.当后轮转动5周后(如图②),前轮的位置是下面四幅图中的第( )幅图。

一、细心思考，认真填写．（每空1分，共22分）1．男生人数的相当于女生人数，是把 看作单位“1”，等量关系式是：男生人数×（ ）=女生人数．2．×+×=×（+），这里运用了 律进行简便运算． 3． 2的倒数是 ；872与 互为倒数；最小合数的倒数是 ； 的倒数是0.5．4. 35 = （ ）∶（ ）= 18（ ）=6÷（ ） 5.甲数的 13 与乙数的 14相等。

如果甲数是90，则乙数是（ ）。

6.小明家在超市的北偏东30°的方向上,距离是300米,超市就在小明家( )偏( )( )的方向上,距离是( )米。

7.丽丽面向北站立，向右转40°后所面对的方向是（ ）；丁丁面向西站立，向左转40°后所面对的方向是（ ）；8.乐乐将20克的糖放入180克的水中，溶解后她喝了这杯糖水的，她喝掉了（ ）克的糖水．9.一个数的倒数是2，这个数的是（ ）10. 20米的54是（ ）米，（ ）米的54是20米。

二、仔细推敲，认真辨析．（正确的打“√”，错误的打“x ”）（10分） 1、a 是b 的 13，b 就是a 的3倍。

（ ） 2、两个分数相除，商一定小于被除数。

（ ）3、真分数一定小于它的倒数。

（ ）4、小明看一本80页的书，第一天看了全书的的 15，第二天应从16页开始看起。

（ ）5、甲数的等于乙数的，甲数一定比乙数小。

（ ）三、选择题。

（12分）1、下面各算式中，结果最大的是（ ）A 、14× 57B 、14÷ 57C 、57÷142、果园里有梨树560棵，（），苹果树有多少棵？列式为：560×（1+）．A．梨树比苹果树多B．梨树比苹果树少C．苹果树比梨树多D．苹果树比梨树少3、一堆煤，昨天用去吨，今天比昨天多用了吨，两天一共用去多少吨？正确算式是（）A．×（1+）B．×（1﹣）C．十D．++4、×（）＞．A．真分数B．大于1的数C．1D．05、两根同样长的电线，第一根用去米，第二根用去，两根电线剩下的部分相比，（）A．第一根长B．两根一样长C．无法确定哪一根长6、如图，书店在超市的（ )方向上。

人教版六年级上册数学竞赛试题一、PK 擂台赛，我能在括号里填上正确的答案。

(每小题2分，共２0分）１． “六(1)班人数是六(2)班人数的76”是把（ )看作单位“1”，（ )占( )的67。

如果六（2)班有４2人,那两个班一共有( ）人。

2.(())=( ）∶( ）＝1４0%=3５÷（ )=（ )。

３. 把73米铁丝平均分成3份，每份长( )米,第二份占全长的(())。

4. 全世界有2０0来个国家，其中缺水的国家有1００多个，严重缺水的国家有40多个。

缺水的国家约占全世界国家总数的（ ）％,严重缺水的国家约占全世界国家总数的（ )%。

5． 某饭店十月份的营业额是３0万元,如果按营业额的5％缴纳营业税，该饭店十月份应缴纳营业税( )元。

6、直径为１0分米的半圆，周长是( )分米。

7. 80%的倒数是（ ),１32的倒数是（ )。

8． 在10０克水中加入25克盐，那么盐水的含盐率是（ ）。

9.85∶0.１25的比值是( ）,化成最简整数比是( ）。

１0． 把一个正方体切成两个小长方体，正方体表面积是两个长方体表面积总和的(())。

二、我是公正小法官,能准确判断是与非。

(对的打“√”，错的打“×”。

5分）11. ４∶5的后项增加1０,要使比值不变，前项应增加８。

（ ） 12. 在32、０.67、６6.7%中最大的数是66.７%。

（ ） 1３． 一个数除以分数的商一定比原来的数大。

( )14． 定价1０0元的商品，先提价２0%，再降价20%,还是原价。

( ） 15. 甲数除以乙数，等于甲数乘乙数的倒数。

( ） 三、快乐ABC,我选得又快又准。

（每小题2分，共10分） 16. 下列图形中,对称轴最少的是( ）A 、长方形B 、正方形C 、等腰三角形 Ｄ、圆 1７. 一个圆的半径扩大４倍，面积扩大（ ）倍。

Ａ、4 Ｂ、8 Ｃ、１6 D 、∏18． 一根长2米的绳子，先用去31，再用去31米，还剩下（ ）米。

(人教版)六年级下册数学竞赛试题一、仔细想，认真填。

（每小题3分，共30分。

）1、北京到天津的实际距离是120千米，在一幅地图上量得两地的图上距离是3厘米，这幅地图的比例尺是（ ）。

2、一个长方形操场，长120米，宽80米。

把它画在比例尺是11000的图纸上，长应画（ ）厘米，宽应画（ ）厘米。

3、把两个完全一样的圆柱，拼成一个长30厘米的圆柱，但表面积减少25.12平方厘米，原来每个圆柱的体积是（ ）立方厘米。

4、一种农药，是用药液和水按照1：1500配制而成的。

如果现在只有4千克的药液，能配制这种农药（ ）千克。

5、一个圆柱的侧面积是188.4平方分米，底面半径是2分米。

它的高是（ ）分米。

6、有两个底面半径相等的圆柱，高的比是3：5。

第二个圆柱的体积是45立方厘米，第二个圆柱的体积比第一个多（ ）立方厘米。

7、用铁皮制作圆柱形通风管10节，每节长80厘米，底面圆的周长是34厘米。

至少需要铁皮（ ）平方米。

8、如果两个比a b 和c d的比值互为倒数，那么a 、b 、c 、d 可以组成的比例是（ ）。

9、有一块正方体的木料，它的棱长是4分米。

把这块木料加工成一个最大的圆柱体，这个圆柱体的体积是（ ）。

10、一个圆锥与一个圆柱的底面积相等。

已知圆锥与圆柱的体积的比是16，圆柱的高是4.8，圆锥的高是（ ）厘米。

三、慎重选择，对号入座。

（每小题2分，共12分。

）1、如果A×2=B÷3，那么A ：B=（ ）① 2：3 ② 3：2 ③1：6 ④6：12、在同时同地测得的杆高和影长（ ）①不成比例 ②成正比例 ③ 成反比例3、如果图上距离3厘米表示实际距离1.5毫米，那么这幅图的比例尺是（ ）①1:20 ②1:2 ③20:14、在比例尺是1 ：8的图纸上，甲、乙两个圆的直径比是2 ：3，那么甲、乙两个圆的实际的直径比是（ ）①1 ：8 ②4 ：9 ③2 ：35、一个圆柱，侧面展开后得到一个正方形，它的高是底面半径的（ ）倍。