基于滑移率试探的电动车辆制动控制策略
- 格式:pdf
- 大小:387.55 KB
- 文档页数:6


电动汽车新能源技术论文范文在污染日益严重、能源日益缺乏的世纪,电动汽车技术的发展给人们带来了新希望。
店铺整理了电动汽车技术论文,希望能对大家有所帮助!电动汽车技术论文篇一:《试谈电动汽车技术》摘要近年来随着经济发展,我国已迈进汽车社会。
汽车保有量迅速增加,导致环境严重污染、交通堵塞等严重问题,因此,为了建设资源节约、环境友好的和谐社会,倡导并鼓励研发、使用环保节能的新能源汽车―电动汽车。
关键词电动汽车动力能源燃料电池前言在污染日益严重、能源日益缺乏的今天,电动汽车的出现给人们带来了新的希望,可以形象地把它称为21世纪的交通工具、明日之星。
电动汽车是一种高新技术产品,它集光、电、机、化等各学科领域中的最新技术于一体,是汽车、电力拖到、功率电子、智能控制、化学电源、计算机、新能源、新材料等工程技术中最新成果的集成物。
从外形上看,电动汽车于常见的汽车并没有什么区别,它们的区别主要在于来自蓄电池。
汽车行驶时,蓄电池电流通过控制器输入到电机中,电机输出扭矩,经离合器、变速器、万向传动装置、主减速器、差速器、半轴等驱动车轮转动。
电动汽车在行驶过程中,不排出任何污染物,噪声也很小,而且不仅不消耗汽油、柴油等石油产品,还可应用多种能源,具有结构简单、使用维修保养方便的特点,是一种新型的交通工具。
1. 电动汽车定义电动汽车是指全部或部分用电能驱动电动机作为动力系统的汽车。
驱动电动汽车的电力常见的有各种蓄电池,燃料电池、太阳能电池等。
2.电动汽车分类电动汽车的种类:纯电动汽车(BEV)、混合动力汽车(HEV)、燃料电池汽车(FCEV)。
2.1纯电动汽车纯电动汽车(BEV):由电动机驱动的汽车。
电动机的驱动电能来源于车载可充电蓄电池或其他能量储存装置。
大部分车辆直接采用电机驱动,有一部分车辆把电动机装在发动机舱内,也有一部分直接以车轮作为四台电动机的转子,其难点在于电力储存技术。
2.2混合动力汽车混合动力汽车指能够至少从下述两类车载储存的能量中获得动力的汽车。

基于目标滑移率的车辆防抱死制动系统控制算法研究
张平平
【期刊名称】《专用汽车》
【年(卷),期】2024()4
【摘要】建立了包含平面内SWIFT轮胎模型在内的四分之一车辆模型,建立了防抱死制动系统模型,并设计了以车轮滑移率为目标,采用PID控制的ABS算法。
基于该平台对ABS控制算法进行仿真,验证其合理性。
最后将ABS控制算法的代码集成到电控制动系统中进行实车试验,试验结果表明,基于目标滑移率的ABS控制算法满足预期。
【总页数】6页(P32-36)
【作者】张平平
【作者单位】芜湖伯特利电子控制系统有限公司
【正文语种】中文
【中图分类】U463.5
【相关文献】
1.基于最佳滑移率的防抱死制动系统的滑模变结构控制
2.前驱电动汽车防抱死制动中滑移率控制的动态负载模拟
3.基于SIMULINK的车辆防抱死制动系统控制研究
4.基于最佳滑移率的电磁-摩擦集成制动器防抱死控制研究
5.复杂路况下高速行驶汽车防抱死制动系统滑移率最优跟踪控制
因版权原因,仅展示原文概要,查看原文内容请购买。


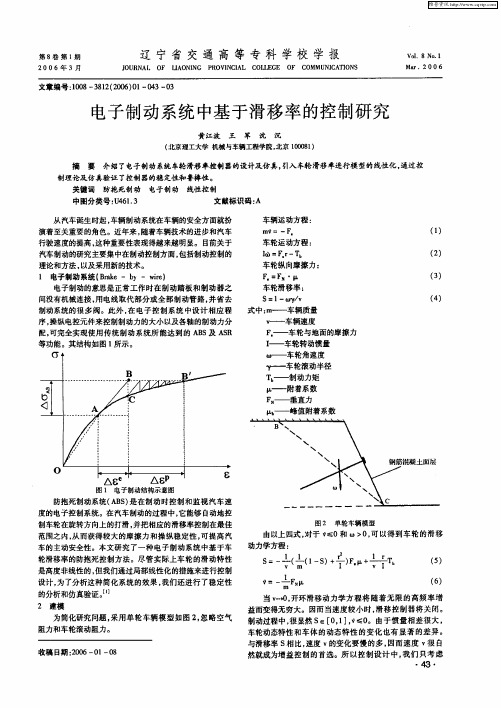
电动汽车再生制动的滑移率控制电动汽车的再生制动是通过电动机的反向工作将运动能转化为电能,再存储到电池中,以提高能源利用率。
然而,如果制动过程中滑移率控制不当,即制动力与车轮滑动不匹配,将会对制动效果和安全性产生很大的影响。
因此,电动汽车在再生制动中需要合理地控制滑移率。
滑移率是指车轮转动速度与车身移动速度之比,可以通过传感器实时检测得到。
通常情况下,电动汽车再生制动的滑移率控制需在0~20%之间,而不是完全锁死车轮L,因为锁死车轮会导致轮胎热变形,制动效果不佳,并且会出现侧滑等失控情况。
为了保证再生制动时的滑移率,电动汽车需要配备专业制动系统。
一般来说,电动汽车再生制动的滑移率控制是通过电控刹车器实现的。
电控刹车器即刹车时点击踏板,汽车内部的控制单元将根据车轮的转速、车速等信息计算合理的电机反向工作强度,将这部分制动力由机械方式转化为电能供电池储存,同时根据设定的滑移率,将剩余的制动力通过刹车片施加到车轮上。
此外,电动汽车的再生制动还可以使用制动辅助系统进行控制。
这种制动辅助系统可以通过调整刹车难度和制动压力,帮助电动汽车实现更精准的再生制动滑移率控制。
同时,制动辅助系统还可以计算车辆本身的重心、负荷分布等因素,帮助电动汽车更好地进行制动以及转向控制。
需要注意的是,电动汽车在雨天或刹车片磨损严重时,制动效果会受到影响,此时对滑移率的控制也需要更加精细。
对于这种情况,电动汽车可通过开启防抱死系统(ABS)实现制动防抱死的同时,进行更加细致的滑移率控制。
总之,电动汽车再生制动是一个非常重要的环节,需要合理地控制滑移率,以确保安全性和能源利用率。
因此,电动汽车制动系统的设计必须优秀,滑移率控制的精准度也必须得到保证。
除了电动汽车再生制动对滑移率的控制外,还有一些其他因素也能影响制动效果和安全性。
其中,路面状况是影响制动效果的一个重要因素。
道路湿滑、结冰等情况下,制动时轮胎和路面之间的摩擦力会下降,导致制动距离变长,制动效果变差。
㊀doi:10.3772/j.issn.1002 ̄0470.2019.03.007基于滑模变结构电驱动防滑刹车控制系统设计张庆利①㊀孔文秦㊀彭㊀波㊀张㊀涛㊀徐方舟(中国运载火箭技术研究院研究与发展中心㊀北京100076)摘㊀要㊀为提高飞机起落架防滑刹车系统的效率和可靠性ꎬ针对刹车系统的复杂性及非线性的特点ꎬ提出了基于滑模变结构的全电驱动刹车防滑控制系统方案ꎻ将滑模变结构的机电设备力闭环的控制策略应用于全电驱动起落架刹车系统ꎬ以提高系统响应频率和刹车力闭环控制精度ꎮ通过惯性台刹车试验对设计的防滑刹车控制器及其控制策略进行验证ꎮ试验结果表明ꎬ设计的电刹车系统带宽由传统算法的2.5Hz提高到7Hzꎬ力闭环控制精度由7.5%FS提高到2.0%FSꎮ关键词㊀滑模变结构ꎬ电驱动ꎬ起落架ꎬ防滑刹车ꎬ控制系统0㊀引言飞机刹车系统是飞机重要的机载设备ꎬ其性能的好坏直接影响到飞机地面运动时着陆及滑跑过程中的高效性㊁稳定性和适应机场跑道的能力ꎮ现代飞机的起降重量与速度越来越大ꎬ对防滑刹车系统提出了更高的要求ꎮ在小结合系数跑道或混合跑道下ꎬ机轮打滑严重ꎬ导致系统刹车效率低ꎬ并很容易使飞机丧失滑跑方向稳定性ꎮ20世纪70年代后期到80年代初ꎬ为了研究恶劣气候条件下ꎬ飞机在小结合系数跑道上着陆时ꎬ防滑刹车系统性能恶化并导致滑跑方向难于操纵的原因ꎬNASA对各种防滑刹车系统进行飞机着陆和试验车轨道试验ꎬ研究各系统在不同跑道状况下的响应与性能[1ꎬ2]ꎮ刹车防滑控制技术经过40多年的发展ꎬ其基本任务就是如何控制和调节机轮刹车时的刹车压力使轮胎不刹死而达到安全滑跑ꎬ从而具有最佳的刹车效果ꎮ为了适应飞机推力㊁载重㊁着陆速度的不断变化ꎬ目前较为成熟且高效的防滑刹车系统工作方式主要分为滑移率刹车控制方式和参考速率 ̄速度差刹车控制方式ꎮ随着多电飞机技术的提出ꎬ采用电作动机构代替传统的液压作动机构已成为航空技术发展的必然趋势ꎮ全电刹车系统采用机电作动机架代替了原来的液压刹车机构ꎬ采用数字式刹车控制器取代了传统的模拟式液压刹车控制器ꎬ具有在系统重量㊁安全性㊁可靠性㊁经济性㊁维护性等诸多方面的优点ꎮ刹车时对不同刹车控制律以及控制律参数的选择ꎬ对飞机刹车效率及刹车系统的稳定性具有重要的影响[3]ꎮ飞机防滑刹车系统分为两大类:脉冲式刹车和打滑监控式刹车ꎮ脉冲式刹车系统工作时ꎬ不管机轮是否打滑ꎬ它按预先设定的时间间隔交替进行刹车㊁松刹ꎬ直到飞机刹停为止ꎮ这类系统的刹车效率次优ꎬ但性能稳定ꎮ打滑监控式刹车系统通过传感器监测飞机的运动ꎬ根据机轮是否打滑进行控制ꎮ这类系统的刹车性能可望达到最优ꎮ脉冲式刹车由于刹车效率低ꎬ不适合未来发展的趋势ꎬ将会慢慢淘汰[4]ꎮ经典控制中PID控制器结构简单ꎬ容易调节ꎬ其设计方法主要有根轨迹法㊁频域响应法等ꎮ根轨迹752㊀高技术通讯2019年第29卷第3期:257~265㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀①男ꎬ1982年生ꎬ博士ꎬ高级工程师ꎻ研究方向:空间机器人技术ꎬ飞行器总体设计ꎬ飞机起落架电气控制技术ꎻ联系人ꎬE ̄mail:zql202qing@163.com(收稿日期:2018 ̄05 ̄05)法通过研究系统开环传递函数的零极点ꎬ设计控制器将闭环系统的传递函数极点设计在希望的位置上ꎬ从而满足系统闭环稳定性能和瞬态性能的要求ꎻ频域响应法通过研究开环传递函数的频域响应ꎬ根据伯德图设计控制器使闭环系统满足设计者对于频域性能的要求ꎮ经典控制理论的控制对象是线性定常系统ꎬ对于非线性系统无法处理ꎬ也不能解决多输入多输出问题[5 ̄7]ꎮ现代控制理论主要包括最优控制法㊁极点配置法㊁卡尔曼滤波法等ꎬ它解决的是多输入多输出问题ꎬ不仅可以用于线性系统ꎬ也可以用于非线性系统[8ꎬ9]ꎮ主要通过极点配置法设计状态反馈控制器将多变量系统的闭环极点配置在期望的位置上ꎬ从而使系统满足设计者提出的瞬态和稳定性能指标[10]ꎮ特别是最优控制理论ꎬ通过对性能的优化可以设计使系统二次型性能指标极小的控制器ꎮ利用线性性能指标设计的线性二次型调节器(LQR控制器)控制效果较好ꎬ控制精度较高[11 ̄13]ꎮ经分析ꎬ当前刹车防滑控制系统方案存在以下缺点ꎮ(1)刹车电机驱动控制在刹车过程中只采用一套PID调节参数ꎬ阶跃信号超调量较大ꎬ控制系统鲁棒性不高ꎮ(2)传统PID+PBM防滑控制器框架结构ꎬ电刹车系统带宽小ꎬ刹车力闭环控制精度较低ꎮ1㊀全电刹车系统的工作原理全电刹车系统包含刹车控制器㊁机电作动控制器㊁电作动机构㊁刹车装置(刹车盘)㊁机轮速度传感器㊁压力传感器等部件ꎮ工作时ꎬ机轮速度信号和飞机速度信号反馈到刹车控制器中ꎬ刹车控制器产生相应的控制信号输出到机电作动控制器(EMA控制器)ꎬ再由EMA控制器产生相应的控制信号控制电作动机构ꎬ从而输出刹车推力作用于压紧盘ꎬ最终压紧刹车动静盘ꎬ动静盘摩擦产生摩擦力改变刹车力矩ꎬ刹车力矩和结合力矩共同控制机轮的转速ꎬ形成一个以机轮速度与刹车力矩为负反馈的双闭环控制系统[14]ꎮ全电刹车系统的工作原理框图如图1所示ꎮ图1㊀全电刹车系统原理框图2㊀电驱动防滑刹车控制器设计2.1㊀刹车机轮数学模型飞机在地面滑跑刹车时ꎬ刹车机轮的刹车装置(刹车盘)产生了阻碍飞机运动的刹车力矩ꎬ路面和刹车机轮之间存在的摩擦力与刹车机轮的滚动半径的乘积为刹车机轮的结合力矩ꎬ刹车装置处于刹车状态时ꎬ刹车力矩比摩擦力矩要大ꎬ此时结合力矩会导致机轮减速ꎬ而在松刹车时ꎬ摩擦力矩大于刹车力矩ꎬ机轮加速转动[15]ꎮ刹车机轮在地面滑跑刹车时的受力简图如图1所示ꎮ图1㊀刹车时机轮受力分析由机轮受力分析可知ꎬ机轮的转动由结合力矩与刹车力矩共同控制ꎬ机轮速度由刹车力矩与结合力矩之差来控制ꎬ即:㊀㊀̇ω=Mj-MbJr(1)852 高技术通讯㊀2019年3月第29卷第3期㊀㊀vr=ωˑRg(2)式中ꎬω㊁̇ω为机轮的角速度及角加速度ꎬMj为结合力矩ꎬMb为刹车力矩ꎬJr为单个机轮转动惯量ꎬvr为机轮的线速度ꎬRg为机轮滚动半径ꎮ影响刹车机轮结合力矩的因素主要有刹车机轮受到的垂向上的载荷㊁刹车机轮滚动半径及轮胎与路面之间的结合系数ꎬ计算公式如下:Mj=fˑRg=μ Pm Rg(3)式中ꎬμ为轮胎与地面结合系数ꎬPm为主机轮受到的垂向载荷ꎮ在建立模型仿真时ꎬ可由刹车推力Pb计算得到刹车力矩ꎬ数学公式如下:Mb=μmc Nmc Pb (Rt+rt)/2(4)其中ꎬμmc为摩擦系数ꎬNmc为摩擦面面数ꎬRt为静盘外半径ꎬrt为动盘内半径ꎮ2.2㊀刹车装置数学模型刹车盘等装置位于机轮轮毂内ꎬ飞机着陆时其动盘由轮毂带动随机轮一起转动ꎬ而静盘通过刹车壳体与轮轴相连ꎬ不随机轮转动ꎬ多片动盘和静盘相互交错装配以增大摩擦面ꎮ当刹车推力由滚珠丝杠送至压紧盘时ꎬ由压紧盘将力均匀地作动到动静盘上ꎬ使动静盘相互挤压ꎮ由于动静盘之间存在相对运动ꎬ因此可产生很大的摩擦力矩ꎬ即刹车力矩ꎬ动静盘之间的动能转换成热量释放出来ꎬ使机轮制动ꎮ由此可知ꎬ刹车装置的主要作用是把传输过来的刹车推力转换成刹车力矩ꎬ同时也是飞机动能被消耗掉的地方ꎮ如果作近似计算ꎬ丝杠从接触刹车盘到压紧刹车盘的过程中丝杠的压紧距离为lꎬ那么刹车推力Pb与l成正比ꎮPb=Ktl㊀㊀㊀Kt为系数(5)2.3㊀机电作动器数学模型全电刹车系统中直流电机的双闭环直流调速系统结构图如图2所示ꎬ其中转速和电流都通过PI调节器进行调节ꎮ将电机模型简化ꎬ主要考虑控制电压和转速的输入输出关系ꎮ直流电机的运动方程为:(1)电枢回路电压平衡公式ua(t)=Ladia(t)dt+Raia(t)+Ea(t)(6)式中ꎬEa(t)为电枢反电势ꎬEa=Ceωm(t)ꎬ其中Ce为反电势系数ꎻωm(t)为电动机转速ꎮ图2㊀直流调速控制系统结构框图(2)电磁转矩方程Mm(t)=Cmia(t)(7)式中ꎬCm为电动机转矩系数ꎬMm(t)为电枢电流产生的电磁转矩ꎮ(3)电机轴上的转矩平衡方程Jmdωm(t)dt=Mm(t)-Mc(t)(8)式中ꎬJm为电机和负载折合到电机轴上的转动惯量ꎬMc(t)为折合到电机轴上的总负载转矩ꎮ由式(4)和式(1)~(3)可得:ua(t)-Ea=Ra(T1dia(t)dt+ia(t))(9)ia(t)-ia1(t)=TmdEa(t)Radt(10)式中ꎬTm为电机机电时间常数ꎻT1为电枢回路电磁时间常数ꎬT1=LaRaꎻia1(t)为负载电流ꎬia1(t)=Mc1(t)CmꎬMc1(t)为电机轴上的负载ꎮ在零初始条件下ꎬ对式(9)㊁(10)的等号两侧进行拉普拉斯变换ꎬ可得到电压与电流间的传递函数为ia(s)ua(s)-Ea(s)=1RaT1s+1(11)电流与电动势间的传递函数为Ea(s)ia(s)-ia1(s)=RaTms(12)由上可得直流电机的动态结构框图ꎬ如图3所示ꎮ952张庆利等:基于滑模变结构电驱动防滑刹车控制系统设计图3㊀直流电机动态结构框图本系统的转速调节器和电流调节器均采用带限幅作用的PI调节器ꎬ而脉冲宽度调制(pulsewidthmodulationꎬPWM)电力电子变换器的传递函数为㊀㊀W(s)=KsTs+1(13)而转速反馈系数α和电流反馈系数βꎬ可根据各个调节器的给定值与反馈值计算有关的反馈系数:㊀㊀α=U∗nmnmax(14)㊀㊀β=U∗imIam(15)式中ꎬU∗nm㊁U∗im分别代表转速环和电流环的最大输入电压ꎬ而nmax和Iam分别代表电机最大转速和最大电流ꎮ最终ꎬ可得直流电机调速系统的数学模型ꎬ如图4所示ꎮ图4㊀直流电机调速系统的数学模型电机驱动滚珠丝杠ꎬ将旋转运动转化为直线运动ꎬ则:ʏωhdt2π=xdL0(16)其中ꎬωh为丝杠送进时的转速ꎬxd为螺母上基准点的轴向位移ꎮ滚珠丝杠旋转一周ꎬ螺母上基准点轴向位移移动L0ꎬ当滚珠丝杠以转速nh送进时ꎬ在时刻t螺母上基准点轴向移动xdꎮ2.4㊀滑移率式PID控制器设计2.4.1㊀控制器输入当刹车制动未启动ꎬ机轮在路面上自由滚动ꎬ不存在相对滑动趋势ꎬ这时轮胎与路面之间仅有滚动摩擦力ꎬ没有滑动摩擦力ꎻ当刹车制动启动后ꎬ轮胎受到了纵向力作用ꎬ轮胎与路面的接触点就会产生纵向的相对运动或者运动趋势ꎬ从而使得轮胎中心的纵向速度与圆周上的线速度产生差异ꎬ可用滑移率来表示这种差异的大小ꎮ滑移率是度量机轮制动程度的一个参数ꎬ其定义是机轮对地面的相对滑动量ꎮ滑移率的计算公式如下:σ=vx-vrvx㊀㊀σɪ[0ꎬ1](17)vr=ωˑRg(18)式中ꎬvx为飞机航向滑跑速度ꎬvr为机轮的线速度ꎬω为机轮转速ꎬRg为机轮滚动半径ꎮ机轮刹车时ꎬ轮胎与地面的摩擦非常复杂ꎬ轮胎与跑道间的结合系数并不是一个常量ꎬ而是受多种因素影响的变量ꎮ理论研究和实践证明ꎬ结合系数受到滑移率的影响最为重要ꎬ由图5可以看出ꎬ要达到最大的结合系数ꎬ就要尽可能控制滑移率在结合系数最大值对应的滑移率附近[16]ꎮ图5㊀滑移率与结合系数之间的关系因此ꎬ采用滑移率控制方式刹车时ꎬ飞机速度信号㊁机轮速度信号经过速度传感器输入到刹车控制器中ꎬ同时测量并采集机轮滚动半径值ꎬ经过计算得到实际滑移率的数值ꎬ计算公式如式(17)和(18)所示ꎮ将计算得到的实际滑移率与最佳滑移率σm=0.2相比ꎬ最佳滑移率与实际滑移率的差值ε=σm-σ作为刹车控制器的输入信号ꎬ输入到PID控制器中进行调节ꎬ期望刹车机轮的实际滑移率始终保持在最佳滑移率附近ꎬ以提高刹车系统的工作效率ꎮ2.4.2㊀防滑刹车控制律设计由于全电刹车系统采用双闭环控制ꎬ控制部分062 高技术通讯㊀2019年3月第29卷第3期既包括对滑移率的控制ꎬ又包括对刹车力矩的控制ꎬ两个控制器均采用PID控制ꎬ其中刹车力矩处在内环ꎬ滑移率处在外环ꎮ整个刹车系统的控制框图如图6所示ꎮ图6㊀全电刹车系统控制框图㊀㊀PID控制算法是利用比例㊁积分㊁微分三个基本环节对系统输入值和反馈的系统输出值进行比较后产生的偏差信号进行一定的处理ꎬ从而实现对系统进行调节控制ꎬ系统一般由PID控制器和被控对象组成ꎬ其原理框图如图7所示ꎮ图7㊀PID控制系统原理图PID控制器根据给定值r(t)与实际输出值y(t)构成控制偏差:e(t)=r(t)-y(t)(22)PID控制规律为u(t)=kPe(t)+kIʏe(t)dt+kDde(t)dt(23)式中ꎬe(t)为系统偏差ꎬu(t)为PID控制器的输出值ꎬkP为比例系数ꎬkI为积分系数ꎬkD为微分系数ꎮ在全电刹车系统中ꎬ给定值r(t)即为最佳滑移率0.2ꎬ实际输出值y(t)为通过速度传感器测得的速度信号计算出来的实际滑移率ꎬ系统偏差e(t)即为最佳滑移率与实际滑移率的差值ꎬu(t)为该速度调节PID控制器的输出值ꎮ若系统偏差为正数ꎬ说明实际滑移率小于最佳滑移率ꎬ机轮处于欠刹车状态ꎬ则输入到刹车力矩控制器的刹车力矩偏差信号值变大ꎬ给刹车电机的电压增大ꎬ电机转速增加ꎬ丝杠前进ꎬ压紧刹车动静盘ꎬ从而增大刹车力矩ꎻ反之ꎬ若系统偏差为负ꎬ说明实际滑移率大于最佳滑移率ꎬ机轮打滑严重ꎬ系统处于过刹车状态ꎬ此时速度调节PID控制器的输出值为负ꎬ输入到刹车力矩控制器的偏差信号也为负ꎬ控制电机反转ꎬ丝杠后退ꎬ松开刹车盘ꎬ达到减小刹车力矩㊁解除机轮打滑严重的现象ꎬ保证滑移率在最佳给定值附近ꎬ提高刹车效率ꎮ速度调节PID控制器的输出值经过放大器Kigꎬ得到速度调节控制器放大器放大的输出值ΔMbꎬ具体公式为ΔMb=Kig u(t)(24)ΔMb也是刹车力矩信号值ꎮ对刹车力矩的控制也采用PID控制方法ꎬ其主要目的是根据输入的目标刹车力矩和实际刹车力矩的差值ꎬ产生输入到电机驱动器的电压信号ꎬ调节直流电机转速ꎬ使实际刹车力矩跟踪目标刹车力矩ꎮ此刻期望的目标刹车力矩由上一时刻的刹车力矩与刹车力矩增量相加得到ꎬ经过一定的放大倍数后与此刻的实际刹车力矩相比较得到误差控制量ꎬ再经过PID控制输出ꎮ具体公式如下:Mbt=Mbm+ΔMb(25)eMb(t)=Mbt-Mbr(26)Mbt为目标刹车力矩ꎬMbm为力矩传感器反馈的上一时刻的刹车力矩ꎬΔMb为速度调节控制器放大器的输出值ꎬMbr为力矩传感器的实际反馈刹车力矩ꎬeMb(t)为刹车力矩调节器的输入偏差值ꎮPID力矩控制器控制规律为uT(t)=kPTeMb(t)+kITʏeMb(t)dt+kDTdeMb(t)dt(27)式中ꎬuT(t)为刹车力矩PID控制器的输出值ꎬkPT为比例系数ꎬkIT为积分系数ꎬkDT为微分系数ꎮ162 张庆利等:基于滑模变结构电驱动防滑刹车控制系统设计刹车力矩PID控制器的输出值uT(t)经过电压放大器Kunꎬ得到刹车电机电压信号ꎬ控制电机正转或反转ꎬ具体公式为Un=Kun uT(t)(28)对于两个PID控制器ꎬ需要分别对其积分环节和微分环节进行饱和值限制ꎬ防止积分器和微分器的输出值超过实际物理取值范围ꎮ速度PID控制器:max(kIʏe(t)dt)ɤaIꎬmax(kDde(t)dt)ɤaDmin(kIʏe(t)dt)ȡbIꎬmin(kDde(t)dt)ȡbD(29)刹车力矩PID控制器:max(kITʏe(t)dt)ɤaITꎬmax(kDTde(t)dt)ɤaDTmin(kITʏe(t)dt)ȡbITꎬmin(kDTde(t)dt)ȡbDT(30)式中ꎬaI为速度PID控制器积分环节的输出上限ꎬaD为速度PID控制器微分环节的输出上限ꎬbI为速度PID控制器积分环节的输出下限ꎬbD为速度PID控制器微分环节的输出下限ꎻaIT为刹车力矩PID控制器积分环节的输出上限ꎬaDT为刹车力矩PID控制器微分环节的输出上限ꎬbIT为刹车力矩PID控制器积分环节的输出下限ꎬbDT为刹车力矩PID控制器微分环节的输出下限ꎮ2.5㊀基于滑模变结构控制器设计滑模切换面设计的目的在于保证系统的稳定性和满足性能指标要求的动态特性ꎬ保证系统状态一旦进入滑模面便能沿其稳定地趋向状态原点ꎮ即使得滑模函数S=0ꎮ在本文设计的防滑刹车控制率中ꎬ飞机防滑刹车控制系统控制的目标是ꎬ维持滑移率保持在最佳滑移率δp不变ꎮ滑移率的公式为㊀㊀δ=x1Rj-x2x2(31)式中ꎬx1为机轮角速度ꎬx2为飞机地速ꎬRj为机轮滚转半径ꎮ因此在整个刹车控制过程中ꎬ要调节机轮的刹车力矩使飞机机轮的滑移率δ=δp恒定不变ꎬ假设力跟踪误差为零ꎬ即x1和x0的比值恒定:x2x1=Rj1+δp(32)针对刹车系统的控制目标ꎬ我们可以定义系统的滑模切换面为S(x)=Cx=1+δpRj-1[]x=x21+δpRj-x1(33)在防滑刹车的过程中ꎬ我们以刹车盘压力为控制对象ꎬ由于t在切换面S=0上的控制力矩是间断的ꎬ可能是正向ꎬ也可能是反向的力矩ꎮ在这里ꎬ我们用某种意义上的力矩平均值(ueq)代替传统的切换控制ꎬ使得刹车系统沿着S=0的切换面移动ꎬ以保证滑动模态的稳定ꎮ对于刹车系统在滑模面的运动ꎬ恒有:S(x)=0ꎬS (x)=0(34)则有以下等式成立:S(x)=x21+δpRj-x1(35)S (x)=̇x21+δpRj-̇x1(36)将式(5)㊁(6)代入式(4)ꎬ根据滑动动力学和防滑刹车系统数学模型ꎬ则有:S (x)=f2(x)1+δpRj-f1(x)+ueqkbI=0(37)经求解得出:ueq=f1(x)-f2(x)1+δpRj[]Ikb(38)令uh=kηꎬkȡIkbꎬ则输出的制动力矩为u=ueq-uh sgn(s)=f1(x)-f2(x)1+δpRj[]Ikb㊀-kη sgn(x21+δpRj-x1)(39)在切换面附近邻域ꎬ由于惯性与滞后的影响ꎬ在滑动运动上通常有一个抖振的叠加分量ꎻ另一方面切换开关的非线性ꎬ也将引起抖动ꎮ抖振不仅会损坏系统的可执行元件ꎬ而且还会引起自激运动ꎬ从而导致系统的不稳定ꎮ采用Ambrosino切换函数法来262高技术通讯㊀2019年3月第29卷第3期削弱变结构控制中的抖振问题ꎬ采用Ambrosino切换函数代替以上符号函数ꎮu=f1(x)-f2(x)1+δpRj[]Ikb-kηs|s|+δ(40)其中ꎬs=x21+δpRj-x13㊀防滑刹车试验3.1㊀传统控制算法的测试结果按照传统的防滑刹车算法ꎬ在某机型的飞机刹车系统在飞机总装状态下ꎬ开展了牵引滑跑试验ꎬ刹车指令和刹车力的响应曲线如图8所示ꎮ图8㊀刹车指令和刹车量响应曲线由上图可知ꎬ飞机飞行控制系统在主轮承载0.65s后开始发出刹车指令ꎮ整个刹车过程中ꎬ左刹车量最大偏差为2.5%ꎬ右刹车量最大偏差为7.1%ꎮ由刹车指令和刹车量的实际响应结果可知ꎬ左右刹车在96.125s时开始进入防滑保护ꎬ并在刹车过程中多次启动防滑保护ꎮ通过分析轮速减速率和刹车控制电流的实际变化曲线(如图9所示)ꎬ当轮速变化超过5m/s2时ꎬ刹车启动相应防滑保护功能ꎻ当轮速变化低于5m/s2时ꎬ刹车响应呈现出恢复趋势ꎬ开始正常响应上位机控制发出的刹车指令ꎬ与防滑保护触发条件的设计状态一致ꎮ由惯性台试验滑跑刹车指令和刹车量响应曲线可知ꎬ系统刹车量偏差较大约为7.1%ꎬ系统响应频率较低ꎮ图9㊀轮速变化和刹车控制电流3.2㊀改进型控制算法的测试结果为了提高系统控制精度和系统响应ꎬ采用本文设计的基于滑模变结构的防滑刹车算法ꎬ在惯性台上开展了防滑刹车性能试验[17]ꎬ通过飞控计算机模拟设备周期性发送不同频率的正弦波刹车力指令信号ꎬ刹车信号响应试验结果如图10~12所示ꎮ由以上试验结果可知ꎬ设计的电刹车系统带宽由传统算法的2.5Hz提高到7Hzꎬ力闭环控制精度由7.5%FS提高到2.0%FSꎮ362 张庆利等:基于滑模变结构电驱动防滑刹车控制系统设计图10㊀2Hz刹车力和刹车指令响应曲线图11㊀7Hz刹车力和刹车指令响应曲线图12㊀刹车力和刹车指令频率交变状态下响应曲线4㊀结论为提高飞机防滑刹车系统的效率和可靠性ꎬ提出了基于滑模变结构的刹车防滑控制系统方案ꎬ以减小系统对阶跃信号超调量ꎬ提高系统刹车力控制精度ꎮ惯性台刹车试验的结果表明ꎬ设计的电刹车系统带宽提高到7Hzꎬ力闭环控制精度由7.1%FS提高到2.0%FSꎮ参考文献[1]李波.飞机防滑刹车系统关键技术研究[D].北京:北京航空航天大学自动化科学与电气工程学院ꎬ2008[2]王纪森.非线性控制理论在防滑刹车系统中的应用研究[D].西安:西北工业大学机电学院ꎬ2001[3]高泽迥.飞机设计手册:起飞着陆系统设计[M].北京:航空工业出版社ꎬ2002[4]TannerJAꎬStubbsSM.Behaviorofaircraftantiskidbrakingsystemsondryandwetrunwaysurfaces:aslip ̄ratio ̄controlledsystemwithgroundspeedreferencefromunbrakednosewheel[J].Brakesꎬ1977.35 ̄42[5]McgowanJA.ExpansionofflightsimulatorcapabilityforstudyandsolutionofaircraftdirectionalcontrolproblemsonrunwaysꎬNASA ̄CR ̄145281[R].Washington:NASAꎬ1978[6]BarnesAG.SimulatorAssessmentofTake ̄offandLand ̄ing[M].Paris:AdvisoryGroupforAeronauticalRe ̄searchandDevelopmentꎬ1963[7]BarnesAGꎬYagerTJ.SimulationofaircraftbehaviouronandclosetothegroundꎬNASA ̄TM ̄87460[R].Washington:NASAꎬ1985[8]HitchH.Aircraftgrounddynamics[J].VehicleSystemDynamicsꎬ1981ꎬ10(4 ̄5):319 ̄332[9]KhapanePD.Simulationofasymmetriclandingandtypi ̄calgroundmaneuversforlargetransportaircraft[J].Aer ̄ospaceScienceandTechnologyꎬ2003ꎬ7(8):611 ̄619[10]ClarkSK.Mechanicsofpneumatictires[J].TechnicalReportArchive&ImageLibraryꎬ1971ꎬ78(3):68[11]PacejkaHB.In ̄planeandout ̄of ̄planedynamicsofpneumatictyres[J].VehicleSystemDynamicsꎬ1981ꎬ10(4 ̄5):221 ̄251[12]SzostakHꎬRosenthalTꎬWadeAR.AninteractivetiremodelfordrivervehiclesimulationꎬSTI ̄TR ̄1227 ̄1 ̄V2[R].Alexandria:NationalTechnicalInformationServ ̄iceꎬ1988[13]PacejkaHBꎬSharpRS.Shearforcedevelopmentbypneumatictyresinsteadystateconditions:areviewof462 高技术通讯㊀2019年3月第29卷第3期modellingaspects[J].VehicleSystemDynamicsꎬ1991ꎬ20(3 ̄4):121 ̄175[14]TakahashiTꎬPacejkaHB.Corneringonunevenroads[J].VehicleSystemDynamicsꎬ1988ꎬ17(S1):469 ̄480[15]徐冬苓ꎬ李玉忍.飞机起落架数学模型的研究[J].系统仿真学报ꎬ2005ꎬ17(4):831 ̄833[16]李玉忍ꎬ薛晶ꎬ马瑞卿ꎬ等.飞机制动过程滑移率寻优方法研究[J].西北工业大学学报ꎬ2008ꎬ26(4):488 ̄491[17]马继杰.制动器惯性台架电模拟惯量性能和关键技术研究[D].长春:吉林大学机电学院ꎬ2010Designofthecontrolsystemofelectricdriveanti ̄skidbrakingsystembasedonslidingmodevariablestructureZhangQingliꎬKongWenqinꎬPengBoꎬZhangTaoꎬXuFangzhou(ResearchandDevelopmentCenterofChinaAcademyofLaunchVihicleTechnologyꎬBeijing100076)AbstractInordertoimprovetheefficiencyandreliabilityoftheaircraft slandinggearanti ̄skidbrakingsystemꎬtheschemeoftheall ̄electricanti ̄skidbrakingcontrolsystembasedonslidingmodevariablestructureisproposedꎬai ̄mingatthecomplexityandnonlinearcharacteristicsofthebrakingsystem.Theforceclosed ̄loopcontrolstrategyofmechanicalandelectricalequipmentwithslidingmodevariablestructureisappliedtotheall ̄electricdrivelandinggearbrakingsystemtoimprovethesystemresponsefrequencyandtheclosed ̄loopcontrolaccuracyofbrakingforce.Thedesignoftheanti ̄skidbrakecontrolleranditscontrolstrategyareverifiedbytheinertialbraketest.Thetestresultsshowthatthebandwidthofthedesignedelectricbrakesystemisincreasedfrom2.5Hzofthetraditionalal ̄gorithmto7Hzꎬandtheforceclosed ̄loopcontrolaccuracyisincreasedfrom7.5%FSto2.0%FS.Keywords:synovialvariablestructureꎬelectricdriveꎬlandinggearꎬanti ̄skidbrakeꎬcontrolsystem562张庆利等:基于滑模变结构电驱动防滑刹车控制系统设计。
公交车基于滑移率的ABS、EBD控制策略研究作者:金彪来源:《科学与财富》2017年第27期摘要:目前ABS已经成为公交车的标配,EBD能够有效辅助ABS制动系统,进一步提高制动效能缩短制动距离,确保车辆平稳行驶。
本文首先阐述了ABS/EBD在不同附着情况下的控制策略,然后基于滑移率选取最佳控制策略为研究对象,建立Carsim的车辆动力学模型,并以Carsim对ABS/EBD控制数据进行仿真模拟,最后通过数据分析得到ABS较为适用PID 控制算法,EBD较为适用逻辑门限控制算法进行车辆制动控制。
关键词:ABS/EBD;仿真分析;控制策略引言稳定的制动方向、短距离制动以及对附着系数的利用是ABS最显著的特点。
然而在汽车制动系统中还有很多的控制缺陷并不是ABS所能解决的。
最突出的就是当车轮滑移率比较小,还没出现在ABS可以监测的范围内,制动压力在每个车轮上分配均匀,但是前车轮和后车轮已经出现对载荷分配的异常改变,前车轮和后车轮没有同时达到滑移时间的最佳点。
本文相对于单一的ABS、EBD在功能上进行了一些调整,它在汽车进行制动的时候,不断地对每一个轮胎与地面的摩擦状况进行计算,并且对制动装置实时加以改变,使制动与摩擦达到相对平衡状态,从而保证车辆制动安全。
1 ABS/EBD控制策略分析1.1 直线行驶制动时的EBD控制策略(1)综合控制减速度与滑移率EBD的介入控制是根据车辆制动时速度下降的幅度不能超过减速度阀值,或者车速下降时的滑移率不得高于设定值。
(2)采用滤波后的后轮减速度与车减速度差值进行控制上述对滑移率进行控制存在一定的技术难度,因为滑移率的参考变量是轮速度,若轮速不精确,则会使滑移率出现偏差,进而影响EBD对应的制动力分配。
若对车速和轮速进行滤波,排除干扰参数,则会有效提高速度的精确度。
(3)基于轮胎影响因素(胎压和温度)下的滑移率控制由于考虑到了轮胎的内部因素,所以该种控制方式更加精确可靠。
基于滑移率的车辆防抱死制动系统控制算法研究的开题报告【摘要】随着汽车行业的飞速发展,车辆防抱死制动系统逐渐成为汽车行业的重要组成部分之一。
基于滑移率的车辆防抱死制动系统控制算法,是一种常用的防抱死制动系统控制策略,其具有效率高、控制精度高等优点。
本文通过分析车辆的动力学模型,对基于滑移率的车辆防抱死制动系统进行了深入研究,并且提出了基于滑移率的制动控制算法,通过仿真实验验证了算法的有效性。
【关键词】车辆防抱死制动系统,基于滑移率,制动控制算法一、研究背景及意义随着汽车行业的快速发展,各种新的汽车技术不断涌现,车辆防抱死制动系统作为一项重要的安全装置开始得到广泛使用。
防抱死制动系统可以有效地防止车辆在急刹车的情况下失控,减少车辆与其他车辆或物体的碰撞事故,提高了车辆行驶的安全性。
基于滑移率的车辆防抱死制动系统控制算法是一种常见的控制策略。
在这种算法中,车辆的轮胎滑动率被用于控制制动力的分配,这可以有效地控制车轮的滑动。
基于此算法的防抱死制动系统具有控制精度高、实施效率高等优点。
因此,对基于滑移率的车辆防抱死制动系统进行深入研究,对于提高车辆行驶安全性具有重要意义。
二、研究内容1.分析车辆动力学模型:通过分析车辆的动力学模型来了解车轮滑动的原因以及滑动率的计算方法。
2.防抱死制动系统控制策略的研究:通过对不同类型的防抱死制动系统控制策略进行研究,选择基于滑移率的控制策略,并分析其原理和优点。
3.基于滑移率的制动控制算法研究:结合车辆动力学模型和防抱死制动系统控制策略,提出一种基于滑移率的制动控制算法,实现对制动力的精确控制,并提高汽车行驶的安全性。
4.仿真实验的设计与验证:建立仿真模型,通过实现基于滑移率的制动控制算法,进行仿真实验,验证算法的有效性。
三、研究计划及进度安排第一阶段:2019年10月-2019年12月阶段任务:研究车辆动力学模型,分析轮胎的滑动原因以及滑移率的计算方法。
阶段成果:完成车辆动力学模型的分析和滑动率的计算方法的研究。