并联电路的电阻

三个并联电阻计算公式以三个并联电阻计算公式为标题，本文将详细介绍三个并联电阻的计算公式及其应用。

一、并联电阻计算公式1. 并联电阻计算公式一：总电阻的倒数等于各个并联电阻倒数之和的倒数。

即：1/Rt = 1/R1 + 1/R2 + 1/R3其中，Rt表示总电阻，R1、R2、R3表示并联电阻的阻值。

这个公式可以用来计算多个并联电阻的总电阻，通过将各个并联电阻的倒数相加再取倒数，得到总电阻的阻值。

2. 并联电阻计算公式二：总电阻等于各个并联电阻之积除以各个并联电阻之和。

即：Rt = (R1 * R2 * R3) / (R1 + R2 + R3)这个公式可以用来计算多个并联电阻的总电阻，通过将各个并联电阻的阻值相乘再除以各个并联电阻的阻值之和，得到总电阻的阻值。

3. 并联电阻计算公式三：总电阻等于各个并联电阻的平均值。

即：Rt = (R1 + R2 + R3) / 3这个公式可以用来计算多个并联电阻的总电阻，通过将各个并联电阻的阻值相加再除以并联电阻的个数，得到总电阻的阻值。

二、并联电阻计算公式的应用并联电阻计算公式广泛应用于电路设计、电子工程和电路分析等领域。

以下是几个具体应用的例子：1. 电路设计：在电路设计中，经常需要计算并联电阻的总电阻。

根据以上三个并联电阻计算公式，可以方便地计算出总电阻的阻值，从而评估电路性能。

2. 电子工程：在电子工程中，常常需要将多个电阻并联起来以达到所需的电阻值。

通过使用并联电阻计算公式，可以确定适合的电阻组合，以满足工程要求。

3. 电路分析：在电路分析中，需要确定电路中的总电阻，以便计算电流和电压。

通过使用并联电阻计算公式，可以准确计算出总电阻的阻值，从而进行电路分析和计算。

三个并联电阻计算公式是电路设计、电子工程和电路分析中常用的工具。

通过运用这些公式，可以方便地计算并联电阻的总电阻，从而评估电路性能、设计适合的电阻组合，并进行电路分析和计算。

熟练掌握这些公式的应用方法，对于电子工程师和电路设计者来说是非常重要的。

并联电路中总电阻公式
并联电阻计算公式是电阻R1和电阻R2串联后，等效为：R串=R1+R2
电阻R1和电阻R2并联后，等效为：(1/R并)=(1/R1)+(1/R2)，或R并
=(R1*R2)/(R1+R2)
并联电路：并联的各支路电压相等，干路电流等于各个支路和。

表达式：电阻R1R2R3……Rn并联，电压U1=U2=……=Un
干路电流：In=I1+I2+……+In由于P=UI，I=U/R，代入，并联电阻的功率比P1：P2：P3……：Pn=U1^2/R1：U2^2/R2……Un^2/Rn=1/R1：R2……1/Rn 由于是纯电阻，发热比Q1：Q2……：Qn=Pn比=1/R1：R2……1/Rn。

扩展资料：
并联电路总电阻越并越小特性这一点和串联电路的总电阻值刚好相反。

如果两只20KΩ相并联，并联后总电阻是其中一只电阻的一半，就是10kΩ。

并联电路中主要矛盾的阻值小的电阻并联电路中，若某一个电阻器的阻值远远大于其它电阻的阻值，则该电阻不起主要作用，可以认为它是开路的。

这样电路中就留下阻值小的电阻器。

分析并联电路时候，就是要抓住阻值小的电阻器，它是这一电路中主要矛盾，即使阻值小的电阻器并联电路中起主要作用，这一点与串联电路正好相反。

电阻并列连接在电路中称为并联电阻，另外由单纯的并联电阻或用电器（用电器：如，电视机，空调，电脑等）构成的电路称为并联电路。

对比于第二个电路，电阻（用电器），依次连接起来的为串联电路。

表达式电阻R1R2R3……Rn并联,电压U1=U2=……=Un干路电流：
In=I1+I2+……+In由于P=UI,I=U
释义
并联的各支路电压相等，干路电流等于各个支路和。

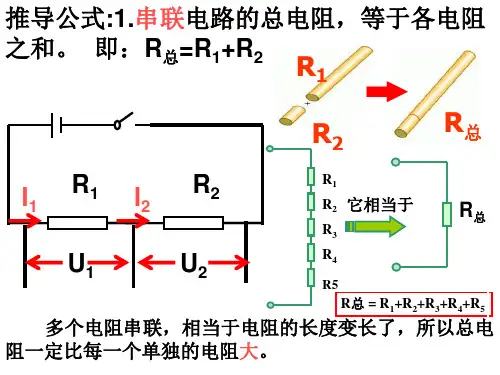
并联电路总电阻公式
并联电路是电流分流的电路，由多个电阻分别连接在电源的两端，其总电阻可以通过以下公式计算：
1.如果并联电路中的每个电阻值相等，那么总电阻可以通过以下公式计算：
1/R总=1/R1+1/R2+1/R3+...+1/Rn
其中，R1、R2、R3、..、Rn分别是并联电路中每个电阻的值。

例如，对于三个相同电阻的并联电路，总电阻为：
1/R总=1/R1+1/R2+1/R3=1/R+1/R+1/R=3/R
所以，总电阻为R总=R/3
2.如果并联电路中的电阻值不相等，那么总电阻需要通过更复杂的公式计算。

首先，求出每个电阻的导纳（Y值）：
Y1=1/R1,Y2=1/R2,Y3=1/R3,...,Yn=1/Rn
然后，求出导纳之和：
Y总=Y1+Y2+Y3+...+Yn
最后，求出总电阻的导纳（Z值）：
Z总=1/Y总
例如，对于三个不同电阻的并联电路，分别为R1、R2、R3，总电阻的计算步骤如下：
Y1=1/R1,Y2=1/R2,Y3=1/R3
Y总=Y1+Y2+Y3
Z总=1/Y总
其中，R1、R2、R3分别是并联电路中每个电阻的值。

总的来说，对于并联电路总电阻的计算，如果电阻值相等，可以使用简化的公式；如果电阻值不相等，需要先求出每个电阻的导纳，然后再进行计算。

这是由于并联电路使得电流分流，所以总电阻会小于每个电阻中最小的一个。

并联电路电阻的计算并联电路是指多个电阻器被连接在一起，两端电压相等，电流分流的电路。

在并联电路中，电阻器的电阻值可以混合使用，不需要保持一致。

在本文中，我们将介绍并联电路电阻的计算方法。

在这个电路中，有两个电阻器R1和R2，它们被连接在一起。

电源提供一个电压V，通过并联电路中的总电流I。

我们的目标是计算出总电阻Rt。

首先，我们需要了解一个重要的定律，欧姆定律。

欧姆定律告诉我们，电流等于电压除以电阻：I=V/R在这个并联电路中，总电流I等于进入电阻器R1的电流I1和进入电阻器R2的电流I2的和：I=I1+I2而电流分流定律告诉我们，电流在分支中分配的比例取决于分支的电阻。

在这个并联电路中，电压相同，所以分支中的电流比例与分支中的电阻相反。

也就是说：I1/I2=R2/R1利用这个关系式，我们可以得到I1和I2之间的关系：I1=I*(R2/(R1+R2))I2=I*(R1/(R1+R2))现在，我们可以将欧姆定律应用到分支电路中，得到每个电阻器的电压：V1=I1*R1V2=I2*R2最后，我们可以将这些结果合并起来，得到总电阻Rt的公式：1/Rt=1/R1+1/R2根据这个公式，我们可以计算出并联电路中两个电阻器的总电阻。

如果有更多的电阻器，我们只需要将它们的电阻值逐一添加到分母中，以此类推。

现在让我们来看一个具体的例子。

假设我们有两个电阻器，R1的电阻值为2欧姆，R2的电阻值为3欧姆。

电源提供的电压为10伏，计算总电阻Rt。

根据之前的公式：1/Rt=1/R1+1/R2代入R1和R2的值：1/Rt=1/2+1/3将分母合并，并计算总电阻Rt：1/Rt=(3/6+2/6)/3=5/6/3=5/18Rt=18/5≈3.6欧姆所以，总电阻Rt约为3.6欧姆。

总结一下，并联电路电阻的计算方法：1.将所有电阻器的倒数求和，得到一个总和值。

2.将总和值的倒数，就得到了并联电路的总电阻。

相对于串联电路，计算并联电路电阻更为简单。

总电阻并联公式总电阻并联公式是电学中一个基础且重要的公式。

在电路中，电流、电压、电阻等物理量都是相互联系的，其中电阻是控制电路流过电流大小的物理量。

在实际应用中，我们常常会遇到多个电阻并联的情况，这时就需要使用总电阻并联公式来求解电路的总电阻。

1. 并联电阻的基本概念在电路中，多个电阻并联指的是电路中多个电阻之间相互串联的情况。

与之相反的是串联电阻，串联电阻指的是电路中多个电阻之间相互并联的情况。

在并联电路中，电流会分流，通过每个电阻的电流大小相等，因此总电流等于各个电阻所通过的电流之和。

根据欧姆定律，电流等于电压除以电阻，因此每个电阻的电压大小相等，因此可以通过对所有电阻的电阻值求取倒数，然后将其相加，再取倒数的方式来求得并联电路的总电阻。

2. 总电阻并联公式假设有 n 个电阻并联，每个电阻分别为 R1、R2… Rn，那么它们的总电阻为：1/R = 1/R1 + 1/R2 + … + 1/Rn其中，R为总电阻。

这个公式也可以表示为：R = R1*R2*…*Rn/(R1 + R2 + … + Rn)换句话说，当电阻并联时，各个电阻的电阻值与其并联后的总电阻有反比关系。

当单个电阻的电阻值变小时，总电阻也相应的变小；当单个电阻的电阻值变大时，总电阻也相应的变大。

3. 举例说明示例1：有两个电阻R1=10Ω 和R2=20Ω，它们并联在一起。

求电路的总电阻 R。

根据总电阻并联公式：R = R1*R2 / (R1+R2) = 10*20 /(10+20) = 6.67Ω示例2：有三个电阻R1 = 12Ω、R2 = 18Ω 和 R3 = 24Ω，它们并联在一起。

求电路的总电阻 R。

根据总电阻并联公式：1/R = 1/R1 + 1/R2 + 1/R3 = 1/12 + 1/18 + 1/24 = 0.2083因此，R=1/0.2083=4.8Ω4. 总结总电阻并联公式是电路电阻计算的基本公式，对于电路分析非常重要。

两个电阻并联后的总电阻
把两个电阻并联后的总电阻有几种计算方式：
1.电阻加法定律：根据电阻加法定律，两个电阻并联后的总电阻Rt = R1 + R2，这里R1和R2代表并联电阻的电阻值。

2.等价电路代换：可以将两个电阻并联后看作是一个电路，电路之间通过电阻来连接，形成一个电流，那么根据等价电路代换法，两个电阻并联后的总电阻Rt的等价电阻为R1 × R2/R1 + R2，也可以用数学公式表示为：
3.电容并联电路：如果两个电阻并联后的电路中有电容C，那么在一定频率下，电容和电阻交互作用会影响到电路的通电性，此时电路的总电阻Rt = | R1 × R2 - (1/ωC)^2 |^1/2，ω为某一特定频率。

4.串联电路：如果将两个电阻是有电容交互作用的，那么两个电阻并联后的电路中就成为串联电路，此时两个电阻并联后的总电阻Rt = 1/ (1/R1 + 1/R2 )。

5.三个并联电阻：如果并联电路中有三块电阻，那么两个电阻并联后的总电阻Rt=1/ (1/R1 + 1/R2 + 1/R3 )，这里R1、R2和R3分别是电阻的值。

以上就是把两个电阻并联后的总电阻的几种计算方式，在工程实践中
可以根据具体情况来采用不同的计算方法。

需要注意的是，在计算时
应当考虑影响电路特性的其它因素，否则可能导致计算结果不准确。

因此，在计算把两个电阻并联后的总电阻时，需要仔细考虑相关因素，以得出更准确的结果。

3并联电阻计算公式
三个电阻并联的公式是：总电阻R总=1/(1/R1+1/R2+1/R3)。

两个电阻并联的公式是：
1/R=1/R1+1/R2。

•3个电阻并联怎么计算？
1具体分析
假设有三个电阻R1，R2，R3
先把R1，R2看作一个整体，记作Ra。

1/Ra=1/R1+1/R2（记为1式）
于是就有：Ra和R3两个电阻并联，记作R总，1/R总=1/R12+1/R3（记为2式）
把1式和2式联立，得：1/R总=1/R1+1/R2+1/R3
所以：R总=1/(1/R1+1/R2+1/R3)
2并联电阻的计算公式
1.电流计算
I总=I1+L2+ (I)
即总电流等于通过各个电阻的电流之和
2.电压计算
U总=U1=U2=……=Un
并联电路各支路两端的电压相等，且等于总电压
3.电阻值计算
1/R总=1/R1+1/R2+……+1/Rn
即总电阻的倒数等于各分电阻的倒数之和
对于n个相等的电阻串联和并联，公式就简化为R串=n*R和R并=R/n
3串联分压，并联分流
原理
在串联电路中，各电阻上的电流相等，各电阻两端的电压之和等于电路总电压。

可知每个电阻上的电压小于电路总电压，故串联电阻分压。

在并联电路中，各电阻两端的电压相等，各电阻上的电流之和等于总电流（干路电流）。

可知每个电阻上的电流小于总电流（干路电流），故并联电阻分流。

电阻的串并联就好像水流，串联只有一条道路，电阻越大，流的越慢，并联的支路越多，电流越大。

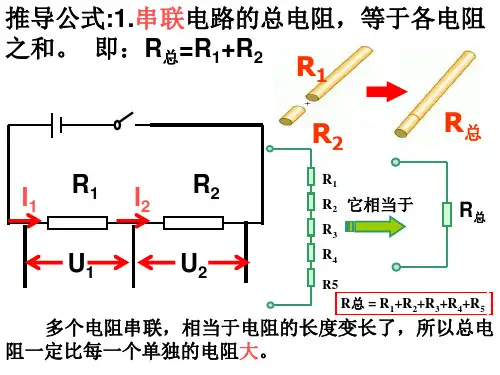
电阻并联后等效电阻并联电阻的总电阻：1/r总=1/r1+1/r2+……+1/rn，即总电阻的倒数等于各分电阻的倒数之和。

特别的，两电阻并联总值为： r总=（r1*r2)/（r1+r2）。

对于n个相等的电阻并联，公式就简化为r并=r/n。

比如说问题中一个电阻20欧，另一个电阻就是40欧，并联在一起总电阻计算方法。

①利用公式 r总=（r1*r2)/（r1+r2）。

r总=20*40/（20+40）=40/3。

②按照电阻并联公式 1/r总=1/r1+1/r2+……+1/rn，将每个分电阻的倒数相加，再求和的倒数就是并联的总电阻。

即1/20+1/40=3/40 那么总电阻就是= 40/3。

①②两种计算结果相同，均就是40/3，相当于13.3。

1、并联电路：并联的各支路电压相等，干路电流等于各个支路和。

表达式：电阻r1r2r3......rn并联,电压u1=u2=......=un干路电流：in=i1+i2+ (i)由于p=ui,i=u/r，代入，并联电阻的功率比p1:p2:p3……：pn=u1^2/r1:u2^2/r2……un^2/rn=1/r1:r2……1/rn由于就是氢铵电阻，咳嗽比q1:q2……：qn=pn比=1/r1:r2……1/rn。

2、并联电路中的关系电压的关系：u=u1=u2。

电流的关系：i=i1+i2。

电阻的关系：1/r=1/r1+1/r2。

电功的计算：w=uit。

电功率的定义式：p=w/t。

常用公式：p=ui焦耳定律：q摆=i^2rt。

对于纯电阻电路而言：q放=i^2rt =u^2t/r=uit=pt=uq=w。

照明设备电路的总功率的排序：p=p1+p1+……。

欧姆定律并联电阻公式
欧姆定律是电学中的基本定律，它表明电流与电阻及电压之间的关系。

在电路中，电阻分为串联电阻和并联电阻两种类型。

对于并联电阻，其总电阻可以通过以下公式计算：
1/总电阻 = 1/电阻1 + 1/电阻2 + 1/电阻3 + ...
其中，电阻1、电阻2、电阻3等为并联电路中的各个电阻值。

与串联电阻不同的是，对于并联电路，电流会分流，通过每个电阻的电流不同，但电压相同。

因此，总电阻应该小于最小的单个电阻，且并联电路的总电流等于各个电阻分支电流之和。

当我们需要计算并联电路中某个电阻的电流时，可以使用欧姆定律公式：
电流 = 电压 / 电阻
其中，电阻为所需计算电阻的阻值，电压为并联电路中的总电压。

通过这个公式，我们可以计算出并联电路中各个分支电阻的电流大小，为电路中的电流分配提供便利。

- 1 -。

如何计算串联电路和并联电路中的总电阻串联电路是指将多个电阻依次连接在一起的电路，而并联电路是指将多个电阻同时连接在电路的两个相同点上。

在计算串联电路和并联电路中的总电阻时，需要遵循一定的公式和方法。

一、串联电路的总电阻计算串联电路中，总电阻等于各电阻的代数和。

即：[ R_{总} = R_1 + R_2 + R_3 + + R_n ]其中，( R_{总} )表示总电阻，( R_1, R_2, R_3, , R_n )分别表示各个电阻的阻值。

二、并联电路的总电阻计算1.等值电阻法并联电路中，总电阻可以通过等值电阻法计算。

等值电阻的倒数等于各并联电阻倒数之和。

即：[ = + + + + ]其中，( R_{总} )表示总电阻，( R_1, R_2, R_3, , R_n )分别表示各个并联电阻的阻值。

并联电路的总电阻还可以通过以下公式计算：[ R_{总} = ]其中，( R_{总} )表示总电阻，( R_1, R_2, R_3, , R_n )分别表示各个并联电阻的阻值。

三、特殊情况下总电阻的计算1.含有多个串联分支的并联电路对于含有多个串联分支的并联电路，首先将每个串联分支的总电阻计算出来，然后再按照并联电路的计算方法求出整个电路的总电阻。

2.含有感性元件和容性元件的电路在含有感性元件和容性元件的电路中，总电阻的计算需要考虑元件的频率特性。

通常情况下，可以使用复数表示法求解。

综上所述，计算串联电路和并联电路中的总电阻需要掌握一定的公式和方法。

在实际应用中，要根据电路的特点和元件的性质选择合适的计算方法。

习题及方法：1.习题：两个电阻 ( R_1 = 5) 和 ( R_2 = 10) 串联连接。

求该串联电路的总电阻。

直接应用串联电路的总电阻公式：[ R_{总} = R_1 + R_2 ]代入电阻值：[ R_{总} = 5+ 10][ R_{总} = 15]答案：串联电路的总电阻为 ( 15)。

2.习题：三个电阻 ( R_1 = 4)，( R_2 = 6) 和 ( R_3 = 8) 串联连接。

并联电路中的总电阻电路是一种由电源、电阻、电容和电感构成的连接电子元件的系统，可以以电流或电压为主要参数进行分析。

电路中最重要的参数就是电阻，因其可以控制电流和电压，因而在电路设计中发挥着重要的作用。

其中，并联电路是经常用到的一种类型的电路，在这种电路中，总电阻也扮演着重要的角色。

电阻是电路中最重要的参数，它确定了电流的大小。

在并联电路中，由多个独立的电阻组成的总电阻与其他电路参数（例如电压和电流）有关。

公式可以用来计算电流与电压之间的关系，如：电压=总电阻*电流，根据此公式可以看出，总电阻越大，电流越小，电压也越小，反之亦然。

总电阻可以通过电路中各个电阻的并联而得到。

并联电路中电阻的类型是独立的，它们的总电阻可以通过简单的公式来计算，即：总电阻=1/（1/R1+1/R2+1/R3+…………………），其中R1、R2、R3…表示电路中各个电阻值。

总电阻对电路参数有着重要的影响，因此在设计电路时，应正确选择各个电阻以确定电路总电阻值，此外还可以通过调整电路中各个电阻的电阻值来调节总电阻与电压和电流之间的关系。

此外，总电阻也会影响电路中其他电子元件的工作，例如晶体管等。

由于晶体管的工作需要特定的电压，当总电阻变化时，也会导致电压的变化，从而影响晶体管的工作。

因此，在设计电路时，应充分考虑到总电阻对晶体管和其他电子元件的影响。

总电阻是电路中不可缺少的参数，它确定了电压与电流之间的关系，并会影响晶体管等其他电子元件的工作，因此，在使用并联电路时，应正确选择电路中各个电阻以确定总电阻，并充分考虑到总电阻对电路参数和电子元件工作的影响。

总之，掌握和正确使用并联电路中的总电阻是我们日常电路设计的重要知识之一，它能有效地控制电路中的电压和电流，同时保证有效的电子元件。

并联电路总电阻摘要：并联电路是电路中的一种连接方式，不同于串联电路，它具有两个或多个电路分支并联连接在一起的特点。

并联电路总电阻是指在并联电路中，所有分支电阻同时连接在电路中所呈现的等效电阻。

本文将介绍并联电路的定义、计算方法和一些相关例题，以帮助读者深入理解并联电路总电阻的概念。

引言：在电路中，我们经常会遇到多个电阻并联连接在一起的情况。

并联电路是电路中常用的一种连接方式，常见于家庭电器、电子设备和工业生产等领域。

了解并联电路总电阻的计算方法和相关特性，对于电路的设计和故障排查具有重要意义。

一、并联电路定义：并联电路是指将两个或多个电阻并联连接在电路中的一种连接方式。

在并联电路中，每个电阻都在电路的两个端点之间，相互独立地与电源连接。

当电路中有多个并联的电阻时，电流可以选择通过不同的电阻，从而使电路中电流的分布出现变化。

二、并联电路总电阻计算方法：在并联电路中，所有的电阻同时连接在电路中，因此电流会选择通过阻值最小的电阻分支。

总电阻即为所有分支电阻的等效电阻，可以通过以下公式计算：1 / Rt = 1 / R1 + 1 / R2 + ... + 1 / Rn其中，Rt为并联电路的总电阻，R1、R2、...、Rn为每个并联电阻的电阻值。

三、并联电路总电阻的特性：1. 并联电路总电阻与分支电阻的关系：在并联电路中，总电阻小于任何一个分支电阻。

这是因为电流会选择通过阻值最小的分支，从而降低了总电阻。

2. 并联电路总电阻的数值特点：在并联电路中，总电阻的数值始终小于分支电阻的最小值。

当电路中的分支电阻都相等时，总电阻等于任意一个分支电阻的数值与分支数的倒数的乘积。

3. 并联电路中的功率分配：在并联电路中，每个分支电路都能独立地吸收电路中的一部分功率，功率的分配比例取决于各分支电阻的大小。

四、并联电路总电阻的应用：1. 并联电路的设计：在电路设计中，我们常常需要计算并联电路的总电阻，以确定电路的工作状态和性能。

两个电阻并联的总电阻r电阻并联是电路中常见的一种连接方式，其特点是两个电阻同时连接在电路中，电流可以选择通过其中任何一个电阻。

并联电路在我们日常生活中有着广泛的应用，比如电灯、电热水壶等家庭电器。

那么，两个电阻并联的总电阻是如何计算的呢？首先，我们来了解一下电阻的概念。

电阻是物体对电流流动的阻碍程度的度量，单位是欧姆（Ω）。

电阻越大，表示对电流的阻碍越高，电流通过的能力就越低。

当两个电阻并联在一起时，它们的端点连接在一起，形成一个电路。

根据欧姆定律（U = I * R），我们知道电压（U）等于电流（I）乘以电阻（R）。

根据并联电路的特性，电流可以选择通过任何一个电阻，所以两个电阻的电压是相等的。

假设两个电阻分别为R1和R2，总电压为U，则根据欧姆定律可得：U = I * R1 (1)U = I * R2 (2)将上述两个式子相除，消去电流I，得到：R1/R2 = U/U = 1这意味着两个电阻并联时，它们的电阻比例恒定为1，即两个电阻相等时，并联电路的总电阻等于它们的一半。

现在我们来具体计算一下。

假设两个电阻分别是10Ω和20Ω，根据上述结论，它们并联时的总电阻为：R = (10Ω * 20Ω) / (10Ω + 20Ω)= 200Ω / 30Ω= 6.67Ω所以，两个电阻分别为10Ω和20Ω时，并联电路的总电阻为6.67Ω。

电阻并联在实际应用中具有重要意义。

比如，当我们在家中安装多个电灯时，为了保证每个电灯都能正常工作，我们通常会将它们并联连接，这样可以确保每个电灯获得相同的电压和充足的电流。

又比如在电路中，我们可能需要控制不同电阻的电流，通过并联这些电阻，可以灵活地调节电流大小。

总之，电阻并联是一种常见的电路连接方式，其总电阻的计算方法简单明了。

掌握了电阻并联的原理和计算方法，我们可以更好地应用在实际生活和工作中，解决各种电路问题，提高电路的稳定性和效率。

希望通过这篇文章的介绍，大家能对电阻并联有更深入的了解，为实际应用提供指导意义。

电阻并联总阻值
电阻并联总阻值是指多个电阻器并联连接时的总体电阻值。

并联电路中的电阻器是各自独立的，电流能够分流流经各个电阻器，因此并联电路的总电阻值会比单一电阻器小。

在并联电路中，每个电阻器的电阻值相同或不同都可以。

如果电阻器的电阻值相同，那么并联电路的总电阻值就是单个电阻器电阻值的倒数再乘以电阻器个数。

如果电阻器的电阻值不同，那么并联电路的总电阻值就需要用到并联电路公式：总电阻值等于各个电阻器电阻值的倒数之和的倒数。

例如，两个电阻器的电阻值分别为R1和R2，它们并联连接，那么并联电路的总电阻值就是：
1/Rt = 1/R1 + 1/R2
Rt = R1 x R2 / (R1 + R2)
如果有三个电阻器并联连接，它们的电阻值分别为R1、R2和R3，那么并联电路的总电阻值就是：
1/Rt = 1/R1 + 1/R2 + 1/R3
Rt = R1 x R2 x R3 / (R1 x R2 + R1 x R3 + R2 x R3) 在实际电路中，电阻并联可以用于将电阻值降低，增加电路的通行能力。

例如，在家庭电路中，多个灯泡可以并联连接，这样可以降低总电阻值，使电路中的电流增加，从而保证灯泡发光。

总之，电阻并联可以有效降低电路的总电阻值，增强电路的通行能力。

掌握并联电路公式，可以帮助我们更好地设计和调试电路。