并联电路的总电阻

串并联电路的电阻（1）串联总电阻=R1+R2+Rn（2）并联电路的电阻计算公式 1/R总=1/R1+1/R2+1/Rn（3）串联电流为I总=I1=I2=I3=I4=In（4）并联电路的电流计算：基本公式有欧姆定律：I=U/R并联电路的电流等于各支路电流之矢量和。

每个支路的电流与导体阻抗有关，导体阻抗小电流大，导体阻抗大电流小。

电流与阻抗的分配遵循线性反比规则，如两阻抗值之比为1：2，则所分配到的电流值为2：1。

并联电路中的干路电流(或说总电流)等于各支路电流之和：I=I1+I2把元件并列地连接起来组成的电路。

并联电路的特点:1.并联电路中各支路的电压都相等，并且等于电源电压：U=U1=U22.并联电路中的干路电流(或说总电流)等于各支路电流之和：I=I1+I23.并联电路中的总电阻的倒数等于各支路电阻的倒数和：1/R=1/R1+1/R2或写为：R=(R1+R2)/R1xR24.并联电路中的各支路电流之比等于各支路电阻的反比：I1/I2=R2/R15.并联电路中各支路的功率之比等于各支路电阻的反比：P1/P2=R2/R1（5）并联电路:并联电路是使在构成并联的电路元件间电流有一条以上的相互独立通路，为电路组成二种基本的方式之一。

特点:电路有多条路径,每一条电路之间互相独立，有一个电路元件短路则会造成电源短路。

干路开关控制所有的用电器，支路开关控制所在支路的用电器。

并联电路中各支路的电压都相等，并且等于电源电压。

U=U1=U2 并联电路中的干路电流(或说总电流)等于各支路电流之和。

I=I1+I2并联电路中的总电阻的倒数等于各支路电阻的倒数和。

1/R=1/R1+1/R2或写为:R=R1*R2/(R1+R2)并联电路中的各支路电流之比等于各支路电阻的反比。

I1/I2=R2/R1并联电路中各支路的功率之比等于各支路电阻的反比。

P1/P2=R2/R1（6）串并联电路，电路实物图画法口诀:首首连接，尾尾相连，首进尾出。

并联电路中的电阻公式并联电路中的电阻公式指的是计算并联电路中总电阻的公式。

在并联电路中，每个电阻都与电源正级和负极相连，因此它们具有相同的电压。

并联电路中，每个电阻的电流取决于其电阻大小。

总电流等于并联电路中各电阻电流的代数和。

在并联电路中，总电阻等于各个并联电阻的倒数的和的倒数。

总电阻的计算公式为：1/RT=1/R1+1/R2+1/R3+...+1/Rn其中RT表示总电阻，R1，R2，R3，...，Rn表示各个并联电阻。

为了更好地理解并联电路中的电阻公式，我们可以通过一个简单的例子来说明。

假设有一个并联电路，其中有三个电阻R1，R2和R3，它们的电阻分别为10欧姆，20欧姆和30欧姆。

我们来计算并联电路的总电阻。

首先，根据电阻公式，我们可以得到：1/RT=1/R1+1/R2+1/R3代入各个电阻的数值，得到：1/RT=1/10+1/20+1/30作为倒数相加的分数，我们可以找到公共分母，然后相加得到：1/RT=(3/30)+(3/60)+(2/60)=8/60对8/60取倒数，得到总电阻RT的值：RT=60/8=7.5欧姆因此，该并联电路的总电阻为7.5欧姆。

除了以上的数值计算，我们还可以通过并联电路的网络原理来推导并联电路中总电阻的公式。

在并联电路中，每个电阻都是独立的，所以电阻越小，电流越大。

因此，较小的电阻会消耗更多的电源电压。

因此，总电阻应该小于或等于各个电阻中的最小值。

另外，我们可以通过欧姆定律来计算并联电路中的电流。

根据欧姆定律，电流等于电压除以电阻。

在并联电路中，电压相同，所以电流取决于电阻大小。

根据电流公式，我们可以得到：I=V/RT其中I表示总电流，V表示电源电压，RT表示总电阻。

通过总电流的公式，我们可以推导出总电阻的公式：RT=V/I因此，总电阻等于电源电压除以总电流。

综上所述，我们可以通过倒数相加法或者欧姆定律来计算并联电路中的总电阻。

这些公式为我们提供了计算并联电路中电阻的方法，并帮助我们分析并联电路的特性和行为。

并联电阻阻值
并联电阻是指两个或多个电阻器同时连接在电路中，它们的两端分别
与电源的正、负极相连。

并联电阻的总电阻值等于各个电阻器的倒数
之和再取倒数。

假设有两个电阻器R1和R2，并联连接在一起，它们的阻值分别为R1和R2。

则它们的总电阻值Rp可以通过以下公式计算：
Rp = (R1 × R2) / (R1 + R2)
如果有三个或更多的电阻器并联连接在一起，则总电阻值Rp可以通过以下公式计算：
Rp = 1 / (1/R1 + 1/R2 + 1/R3 + ...)
需要注意的是，当其中一个电阻器短路或断路时，整个并联电路将无
法工作。

因此，在设计并联电路时需要仔细考虑每个电阻器的质量和
可靠性。

总之，对于任意数量的并联电阻，其总电阻值都可以通过以上公式进
行计算。

掌握这些基本知识可以帮助我们更好地理解并应用并联电路。

欧姆定律并联电阻公式
欧姆定律是电学中的基本定律，它表明电流与电阻及电压之间的关系。

在电路中，电阻分为串联电阻和并联电阻两种类型。

对于并联电阻，其总电阻可以通过以下公式计算：
1/总电阻 = 1/电阻1 + 1/电阻2 + 1/电阻3 + ...
其中，电阻1、电阻2、电阻3等为并联电路中的各个电阻值。

与串联电阻不同的是，对于并联电路，电流会分流，通过每个电阻的电流不同，但电压相同。

因此，总电阻应该小于最小的单个电阻，且并联电路的总电流等于各个电阻分支电流之和。

当我们需要计算并联电路中某个电阻的电流时，可以使用欧姆定律公式：
电流 = 电压 / 电阻
其中，电阻为所需计算电阻的阻值，电压为并联电路中的总电压。

通过这个公式，我们可以计算出并联电路中各个分支电阻的电流大小，为电路中的电流分配提供便利。

- 1 -。

并联的电阻
并联的电阻是电路中常见的一种连接方式，它可以有效地改变电路的总电阻。

在并联电路中，电流会分流通过不同的电阻，从而使得总电阻变小。

当多个电阻并联连接时，它们的两端都连接在一起，形成一个共同的节点。

从这个节点出发的电流会被分流到不同的电阻上，每个电阻上的电流大小取决于电阻的大小。

这样，电流在并联电路中会分成多个分支，通过各个分支的电阻后再汇总到一个节点上，形成总电流。

并联的电阻可以通过以下方式计算总电阻：
1. 如果并联的电阻都是相等的，那么总电阻等于每个电阻的阻值除以电阻的个数。

例如，如果有两个相等的电阻并联连接，那么总电阻等于每个电阻的阻值的一半。

2. 如果并联的电阻不相等，那么可以使用公式：总电阻的倒数等于每个电阻的倒数之和。

例如，如果有两个不相等的电阻并联连接，那么总电阻的倒数等于每个电阻的倒数之和。

并联的电阻在电路中有着广泛的应用。

它可以用来控制电路的总电阻，从而调节电路中的电流和电压。

在家庭电路中，我们常常使用并联电阻来连接电器设备，以便提供所需的电流和电压。

在电子电路中，我们也经常使用并联电阻来调节电路的工作状态，以满足不同的需求。

总的来说，并联的电阻是电路中一种常见的连接方式，它可以有效地改变电路的总电阻。

通过控制并联电阻的数量和阻值，我们可以调节电路中的电流和电压，从而满足不同的需求。

并联的电阻在电路设计和应用中发挥着重要的作用，对于我们理解和应用电路有着重要的意义。

如何计算串联电路和并联电路中的总电阻串联电路是指将多个电阻依次连接在一起的电路，而并联电路是指将多个电阻同时连接在电路的两个相同点上。

在计算串联电路和并联电路中的总电阻时，需要遵循一定的公式和方法。

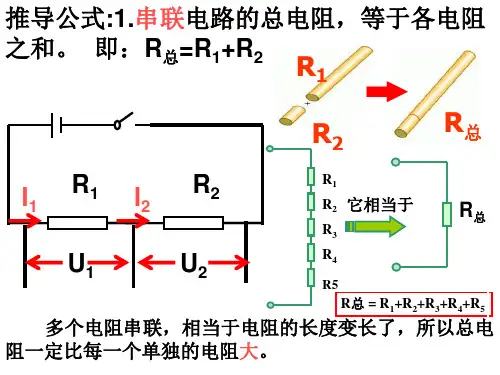
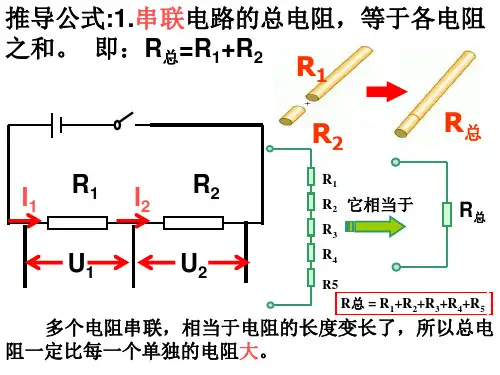
一、串联电路的总电阻计算串联电路中，总电阻等于各电阻的代数和。

即：[ R_{总} = R_1 + R_2 + R_3 + + R_n ]其中，( R_{总} )表示总电阻，( R_1, R_2, R_3, , R_n )分别表示各个电阻的阻值。

二、并联电路的总电阻计算1.等值电阻法并联电路中，总电阻可以通过等值电阻法计算。

等值电阻的倒数等于各并联电阻倒数之和。

即：[ = + + + + ]其中，( R_{总} )表示总电阻，( R_1, R_2, R_3, , R_n )分别表示各个并联电阻的阻值。

并联电路的总电阻还可以通过以下公式计算：[ R_{总} = ]其中，( R_{总} )表示总电阻，( R_1, R_2, R_3, , R_n )分别表示各个并联电阻的阻值。

三、特殊情况下总电阻的计算1.含有多个串联分支的并联电路对于含有多个串联分支的并联电路，首先将每个串联分支的总电阻计算出来，然后再按照并联电路的计算方法求出整个电路的总电阻。

2.含有感性元件和容性元件的电路在含有感性元件和容性元件的电路中，总电阻的计算需要考虑元件的频率特性。

通常情况下，可以使用复数表示法求解。

综上所述，计算串联电路和并联电路中的总电阻需要掌握一定的公式和方法。

在实际应用中，要根据电路的特点和元件的性质选择合适的计算方法。

习题及方法：1.习题：两个电阻 ( R_1 = 5) 和 ( R_2 = 10) 串联连接。

求该串联电路的总电阻。

直接应用串联电路的总电阻公式：[ R_{总} = R_1 + R_2 ]代入电阻值：[ R_{总} = 5+ 10][ R_{总} = 15]答案：串联电路的总电阻为 ( 15)。

2.习题：三个电阻 ( R_1 = 4)，( R_2 = 6) 和 ( R_3 = 8) 串联连接。

如何计算电路中的电阻总和电路中的电阻总和是指电路中所有电阻的累加值。

在电路设计和分析中，计算电阻总和是非常重要的，它可以帮助我们理解电路的特性和性能。

本文将介绍如何计算电路中的电阻总和，包括串联电阻和并联电阻的计算方法，并提供一些实例来帮助读者更好地理解。

一、串联电阻的计算方法串联电阻是指电路中多个电阻依次连接在一起，电流依次通过它们。

计算串联电阻的方法很简单，只需将各个电阻的电阻值相加即可。

例如，假设有一个串联电路，其中有三个电阻，分别为R1、R2和R3。

它们的电阻值分别为10欧姆、20欧姆和30欧姆。

我们可以使用下列公式计算串联电阻的总和（RT）：RT = R1 + R2 + R3= 10 + 20 + 30= 60欧姆这样，串联电路中的电阻总和为60欧姆。

二、并联电阻的计算方法并联电阻是指电路中多个电阻同时连接在一起，它们两端具有相同的电压。

计算并联电阻的方法稍微复杂一些，要使用电阻的倒数进行计算。

假设有一个并联电路，其中有三个电阻，分别为R1、R2和R3。

我们可以使用下列公式计算并联电阻的总和（RT）：1/RT = (1/R1) + (1/R2) + (1/R3)= (1/10) + (1/20) + (1/30)我们将上式分母通分并求倒数，然后进行计算：1/RT = [(60 + 30 + 20) / (10 * 20 * 30)]= (110 / 6000)≈ 0.018再将等式两边取倒数，即可得到并联电路中的电阻总和：RT = 1 / (1/RT)= 1 / 0.018≈ 55.56欧姆这样，对于一个并联电路，其中的电阻总和约为55.56欧姆。

三、串联和并联电阻的混合计算方法在实际的电路中，常常既存在串联电阻，又存在并联电阻。

对于这种情况，我们可以先计算出串联电阻的总和，再将这个总和与并联电阻的总和进行处理。

例如，考虑一个电路，其中有四个电阻，其中前三个电阻（R1、R2和R3）串联连接，与第四个电阻（R4）并联连接。

两个电阻并联的总电阻公式电阻是电子元件中最基础的元件之一，可以用来限制电流的流动。

在电路中，电阻可以串联或并联，而并联电阻的总电阻是两个电阻的倒数之和。

下面将就此进行详细探讨。

我们需要了解电阻的定义和单位。

电阻是指电流通过时，电压降低的程度，单位是欧姆（Ω）。

一般来说，电阻越大，通过电流越小，电压降低越多。

电阻的大小与电阻器的材质、长度、截面积、温度等因素有关。

当两个电阻并联时，它们之间的电压相等，而电流则分别通过两个电阻。

根据欧姆定律，电流与电阻成反比例关系，因此电流较大的电阻其阻值较小，电流较小的电阻其阻值较大。

这样就可以得到并联电阻的总电阻公式，即两个电阻的倒数之和。

例如，当两个电阻分别为R1=10Ω和R2=20Ω时，它们并联后的总电阻为：1/R = 1/R1 + 1/R21/R = 1/10 + 1/201/R = 3/20R = 20/3 ≈ 6.67Ω总电阻为6.67Ω，比两个电阻中较小的10Ω要小，而比较大的20Ω要大。

这是因为电阻并联后，相当于增加了一条电路，电流可以选择通过其中任意一条，因此总电阻会变小。

在实际电路中，电阻并联常常用于调节电路中的电阻值，以控制电路的性质。

例如，在放大器电路中，可以通过并联电阻来调节放大器的增益，以达到最佳效果。

除了两个电阻并联，多个电阻也可以并联，总电阻的计算方式也相同。

例如，三个电阻R1、R2、R3并联后的总电阻为：1/R = 1/R1 + 1/R2 + 1/R3电阻并联是电路中常用的一种电路连接方式。

通过两个电阻并联的总电阻公式，可以计算出并联电阻的总电阻，以便电路设计和调节。

并联电路电阻的计算并联电路是指多个电阻器被连接在一起，两端电压相等，电流分流的电路。

在并联电路中，电阻器的电阻值可以混合使用，不需要保持一致。

在本文中，我们将介绍并联电路电阻的计算方法。

在这个电路中，有两个电阻器R1和R2，它们被连接在一起。

电源提供一个电压V，通过并联电路中的总电流I。

我们的目标是计算出总电阻Rt。

首先，我们需要了解一个重要的定律，欧姆定律。

欧姆定律告诉我们，电流等于电压除以电阻：I=V/R在这个并联电路中，总电流I等于进入电阻器R1的电流I1和进入电阻器R2的电流I2的和：I=I1+I2而电流分流定律告诉我们，电流在分支中分配的比例取决于分支的电阻。

在这个并联电路中，电压相同，所以分支中的电流比例与分支中的电阻相反。

也就是说：I1/I2=R2/R1利用这个关系式，我们可以得到I1和I2之间的关系：I1=I*(R2/(R1+R2))I2=I*(R1/(R1+R2))现在，我们可以将欧姆定律应用到分支电路中，得到每个电阻器的电压：V1=I1*R1V2=I2*R2最后，我们可以将这些结果合并起来，得到总电阻Rt的公式：1/Rt=1/R1+1/R2根据这个公式，我们可以计算出并联电路中两个电阻器的总电阻。

如果有更多的电阻器，我们只需要将它们的电阻值逐一添加到分母中，以此类推。

现在让我们来看一个具体的例子。

假设我们有两个电阻器，R1的电阻值为2欧姆，R2的电阻值为3欧姆。

电源提供的电压为10伏，计算总电阻Rt。

根据之前的公式：1/Rt=1/R1+1/R2代入R1和R2的值：1/Rt=1/2+1/3将分母合并，并计算总电阻Rt：1/Rt=(3/6+2/6)/3=5/6/3=5/18Rt=18/5≈3.6欧姆所以，总电阻Rt约为3.6欧姆。

总结一下，并联电路电阻的计算方法：1.将所有电阻器的倒数求和，得到一个总和值。

2.将总和值的倒数，就得到了并联电路的总电阻。

相对于串联电路，计算并联电路电阻更为简单。

并联等效电阻的求法并联电阻的总电阻：1/r总=1/r1+1/r2+……+1/rn，即总电阻的倒数等于各分电阻的倒数之和。

特别的，两电阻并联总值为： r总=（r1*r2)/（r1+r2）。

对于n个相等的电阻并联，公式就简化为r并=r/n。

比如说问题中一个电阻20欧，另一个电阻就是40欧，并联在一起总电阻计算方法。

①利用公式 r总=（r1*r2)/（r1+r2）。

r总=20*40/（20+40）=40/3。

②按照电阻并联公式 1/r总=1/r1+1/r2+……+1/rn，将每个分电阻的倒数相加，再求和的倒数就是并联的总电阻。

即1/20+1/40=3/40 那么总电阻就是= 40/3。

①②两种计算结果相同，均就是40/3，相当于13.3。

1、并联电路：并联的各支路电压相等，干路电流等于各个支路和。

表达式：电阻r1r2r3......rn并联,电压u1=u2=......=un干路电流：in=i1+i2+ (i)由于p=ui,i=u/r，代入，并联电阻的功率比p1:p2:p3……：pn=u1^2/r1:u2^2/r2……un^2/rn=1/r1:r2……1/rn由于就是氢铵电阻，咳嗽比q1:q2……：qn=pn比=1/r1:r2……1/rn。

2、并联电路中的关系电压的关系：u=u1=u2。

电流的关系：i=i1+i2。

电阻的关系：1/r=1/r1+1/r2。

电功的计算：w=uit。

电功率的定义式：p=w/t。

常用公式：p=ui焦耳定律：q摆=i^2rt。

对于纯电阻电路而言：q放=i^2rt =u^2t/r=uit=pt=uq=w。

照明设备电路的总功率的排序：p=p1+p1+……。

并联电阻总电阻与各分电阻的关系电阻是电路中常见的元件，它用于控制电流的流动。

在电路中，电阻可以串联或并联连接。

本文将重点讨论并联电阻的总电阻与各分电阻之间的关系。

在并联电路中，多个电阻以并联的方式连接在一起。

这意味着它们的两端相连，形成一个共同的节点。

根据欧姆定律，电流会根据电阻的阻值分配到各个分支上。

而并联电阻的总电阻会受到各分电阻的影响。

我们需要了解并联电阻的计算公式。

在电路中，如果有n个并联电阻R1，R2，...，Rn，它们的总电阻Rp可以通过以下公式计算得出：1/Rp = 1/R1 + 1/R2 + ... + 1/Rn这个公式称为并联电阻的倒数定律。

它告诉我们，总电阻的倒数等于各分电阻倒数之和的总和的倒数。

通过这个公式，我们可以计算出并联电阻的总电阻。

接下来，我们来讨论总电阻与各分电阻之间的关系。

根据并联电阻的计算公式，我们可以得出以下结论：1. 当并联电路中的各分电阻相等时，总电阻等于各分电阻的倒数的和的倒数。

换句话说，各分电阻越小，总电阻越大。

这是因为电流会选择阻值较小的分支流过，导致总电阻增加。

2. 当并联电路中的各分电阻不相等时，总电阻会小于各分电阻中最小的阻值。

这是因为电流会倾向于流过阻值较小的分支，导致总电阻减小。

总电阻与各分电阻之间的关系可以用简单的公式表示，而这个公式可以帮助我们计算并联电阻的总电阻。

在实际应用中，了解并联电阻的总电阻与各分电阻之间的关系对于电路设计和分析非常重要。

除了计算总电阻，了解并联电阻的关系还可以帮助我们理解电路中的电流分配和电压分配。

在并联电路中，电流会根据各分电阻的阻值分配到不同的分支上，而电压在各分支上是相等的。

这些理论可以帮助我们分析并联电路中的电流和电压情况，从而更好地理解电路的工作原理。

并联电阻的总电阻与各分电阻之间存在着明确的关系。

通过计算并联电阻的总电阻，我们可以更好地理解并分析电路中电流和电压的分配情况。

同时，了解并联电阻的关系也对于电路设计和分析非常有帮助。