并联电路讲解：并联电阻、电压、电流的大小及相互关系

Word-可编辑并联电路（基础）责编：冯保国【学习目标】1．理解并联电路的特点，能够区别串、并联电路；2．会衔接容易的并联电路；3．知道并联电路中电流、电压、电阻的逻辑；4．能够将并联电路中电流、电压、电阻的特点和欧姆定律结合起来解决相关的问题。

【要点梳理】要点一、并联电路1.并联电路：把元件并列衔接起来组成的电路。

2.并联电路的特点：①衔接特点：并列衔接---首首尾尾相连。

②电流路径：电流有两条(或多条)路径；③用电器工作特点：各元件可以自立工作，一个灯坏了，其它灯还亮。

④开关控制特点：干路的开关控制囫囵干路，支路的开关只控制本支路。

要点诠释：1.并联电路从电源正极出发在分流点分成几条支路，在汇流点集合流回电源负极，如图1所示，A点是分流点，B点是汇流点，从电源正极到A点，电源负极到B点是干路，A点和B点间是支路。

2.节点法判断串并联电路：①找节点找出“”字和“丅”字在图中标出如图2中的A、B、C、D四点；②找出每个“节点”衔接电源的正极还是负极主意：倘若节点只经过导线和正极相连就标“+”如：A点、B点，倘若只经过导线和负极相连就标“-”如图C点和D点；千里之行，始于足下③如图2所示，三个小灯泡的电流从正极流向负极（绿色箭头标出），所以电路是并联，电流路径如图3所示。

3.生活中的并联电路：①装点天安门等巍峨建造物上的成千上万只灯泡是并联的，浦江游船上的彩灯是并联的（如图4），家庭中各用电器都是并联的，街道两旁的路灯是并联的，比赛时的抢答器的电路是并联的，电冰箱中的灯泡和发动机之间是并联的。

②家庭电路图可简化成下图5所示：电路中的灯泡、电视机、台灯以及小彩灯的整体是并联方式接在电路中的，灯泡和开关是串联，单个小彩灯是串联。

要点二、电路图与实物图的转化1、按照电路图衔接实物图：朽木易折，金石可镂①先通后补：从电源正极出发，先画出电路元件最多的一条通路；找到分流点和汇流点，再将其它支路分离连到分流点和汇流点。

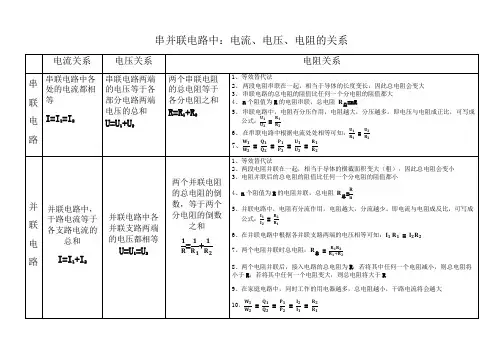
串联和并联是电路中常见的两种连接方式，它们在电流、电压和电阻之间有着不同的关系。

下面我们来详细了解一下串联和并联的电流、电压和电阻的关系。

一、串联电路的电流、电压和电阻关系1. 串联电路的电流：在串联电路中，电流只有一条路径可走，因此串联电路中的电流是相等的。

也就是说，串联电路中每个电阻上的电流都相同。

2. 串联电路的电压：在串联电路中，各个元件的电压之和等于总电压，即串联电路中的电压是相加的。

这是由基尔霍夫电压定律可得出的结论。

3. 串联电路的电阻：在串联电路中，各个电阻直接相加得到总电阻。

这也是由基尔霍夫电流定律可得出的结论。

二、并联电路的电流、电压和电阻关系1. 并联电路的电流：在并联电路中，电流可选择不同的路径进行流动，因此并联电路中的电流是分流的，即各个支路上的电流之和等于总电流。

2. 并联电路的电压：在并联电路中，各个支路上的电压相等，等于总电压。

也就是说，在并联电路中，各个支路上的电压相同。

3. 并联电路的电阻：在并联电路中，各个支路的电阻经过计算得到并联后的总电阻。

计算方式是利用电阻公式的倒数之和再取倒数。

三、串联和并联电路的不同之处1. 串联电路中的电流相等，电压相加，电阻直接相加；而并联电路中的电流分流，电压相等，电阻取倒数相加再取倒数。

2. 串联电路中的总电阻大于任意一个电阻的值，而并联电路中的总电阻小于任意一个电阻的值。

3. 串联电路中的总电压等于各个元件电压之和，而并联电路中的总电压等于各个支路的电压值。

串联和并联的电流、电压和电阻之间有着微妙的关系。

在实际应用中，根据不同的需求和情况，选择合适的串联或者并联连接方式来构建电路，是非常重要的。

对于电流、电压和电阻的关系要有清晰的理解，才能更好地分析和设计电路。

四、串并联混合电路的分析除了纯粹的串联电路和并联电路之外，还有一种常见的电路连接方式，即串并联混合电路。

在串并联混合电路中，电路中既有串联连接，又有并联连接。

这种情况下，需要对电流、电压和电阻进行更为复杂的分析。

串联和并联电阻电压和电流的关系在电路中，电阻是一个非常基础而重要的元件。

而串联和并联是常见的两种电阻连接方式。

它们对电路中电压和电流的分布有着重要的影响。

下面，我将从深度和广度两个方面探讨串联和并联电阻对电压和电流的影响。

一、串联电阻电压和电流的关系1. 串联电阻的电压关系在串联电路中，电压会分别作用在每一个电阻上。

根据基尔霍夫电压定律，串联电路中各个电阻上的电压之和等于串联电路两端的电压。

可以得出串联电阻的电压关系公式为：Ut=U1+U2+...+Un，其中U 表示电压。

2. 串联电阻的电流关系在串联电路中，电流的大小是相同的，因为整个电路中只有一条路径供电流流动。

根据欧姆定律，串联电路中的总电流等于串联电路两端的电压与串联电路总电阻的比值。

可以得出串联电阻的电流关系公式为：It=U/Rt，其中I表示电流，R表示电阻。

二、并联电阻电压和电流的关系1. 并联电阻的电压关系在并联电路中，每个电阻上的电压相同，等于并联电路两端的电压。

并联电阻的电压关系公式为：Ut=U1=U2=...=Un，其中U表示电压。

2. 并联电阻的电流关系在并联电路中，电流会分别通过每一个电阻，且各个电阻上的电流之和等于整个并联电路的总电流。

并联电阻的电流关系公式为：It=I1+I2+...+In，其中I表示电流。

总结回顾通过以上分析可以看出，串联电阻和并联电阻在电压和电流的分布上有着不同的影响。

在串联电路中，电压会分别作用在每一个电阻上，而电流大小相同；而在并联电路中，每个电阻上的电压相同，但电流会分别通过每一个电阻。

个人观点和理解我个人认为，深入理解串联和并联电阻对电压和电流的影响，有助于我们更好地设计和分析电路。

在实际应用中，根据具体的电路需求，选择合适的电阻连接方式，可以更好地满足电路的要求，提高电路的效率和稳定性。

串联和并联电阻在电路中起着重要的作用，它们对电压和电流的分布有着重要影响。

在实际应用中，我们需要深入理解它们的原理和关系，以便更好地应用于实际电路设计和分析中。

串并联电路电流、电压、电阻特点总结-标准化文件发布号：（9556-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII串、并联电路电流、电压和电阻的特点一、电流特点：1、串联电路中各处的电流均相等；公式：2、并联电路中干路电流等于各支路中电流之和；公式：二、电压特点：1、串联电路总电压等于各部分电路两端电压之和；公式：2、并联电路中各支路两端的电压均相等，并且都等于电源电压；公式：三、电阻特点：电阻的串联1、（1）电阻串联越多电路总电电阻越大，因为电阻串联相当于增加了导体的长度。

（2）串联电路有分压作用，电阻越大分压越大。

2、串联电路的总电阻等于各串联电阻之和。

3、电阻串联的公式：（1）R=R1+R2+…+R n（2）n个相同的电阻R串联，总电阻R串=n R4、在下边空白处证明串联电路的电阻特点：电阻的并联1、电阻并联越多电路总电阻越小，电阻并联相当于增大了导体的横截面积。

（同时并联使用的用电器越多，电路的总电流越大）2、并联电路总电阻的倒数等于各并联电阻倒数之和。

3、电阻并联公式：（1）R1=11R+21R+……+n R1（2）n个相同的电阻R并联，总电阻R并=nR4、在下边空白处证明并联电路的电阻特点：5、两个电阻并联时：（在下边空白处推出计算关系）26、（1）几个电阻并联，只要其中一个电阻增大，电路的总电阻也随之增大；（2）滑动变阻器无论串联还是并联，只要自身阻值增大，电路中的总电阻也随之增大。

四、综合应用：1、下图中分析甲乙两电阻的大小(1) (2)2、同种材料制成的导体，粗细不均，AB=BC，按图中方式接入电路。

则R AB R BC，I AB I BC,U AB U BC3、已知R1:R2:R3=1:2:3，则（1）若三个电阻串联时，I1:I2:I3= ,U1:U2:U3= ;（2）若三个电阻并联时，I1:I2:I3= ,U1:U2:U3= 。

4、三个相同电阻R同时接入电路中，可以接出4个不同的总电阻值，分别为：其它测电阻的方法1、利用电流表、定值电阻R0，测未知电阻R X的阻值。

并联电流电压关系解释说明以及概述1. 引言1.1 概述在电路中，电流和电压是两个基本概念，它们在并联电路中有着密切的关系。

并联电路是指多个电子元件或部件以并联形式连接在一起，并在共同的两个节点上接入相同的电源。

在这种情况下，我们对于并联电路中的电流和电压之间的关系进行研究与探索。

1.2 文章结构本文将首先介绍并联电流和电压的基本概念，然后解释并讨论了并联电路的基本原理。

接下来，我们将详细说明并联电路中电流和电压之间的关系，并介绍了相关现象和实际应用场景。

最后，在结论部分总结并证明了所述的并联电流、。

1.3 目的本文旨在深入理解并说明并联电流与电压的关系，并解释其背后所包含的原理。

通过对相关概念、原理和现象进行阐述，读者将能够更好地理解、分析和应用于实际工程中。

此外，文章还提供了一些实际应用场景以及未来发展前景，以帮助读者更好地理解该主题的重要性。

2. 并联电流电压关系2.1 电流和电压的概念在讨论并联电流电压关系之前，我们首先需要了解电流和电压的概念。

简单来说，电流是指单位时间内通过某一点的电荷量，通常以安培（A）作为单位表示；而电压则是指单位正电荷带有的能量或单位正负极之间的势能差，通常以伏特（V）作为单位表示。

2.2 并联电路的基本原理并联电路由两个或多个分支组成，这些分支都连接到相同的起始节点和结束节点。

在并联电路中，各个分支之间是同时连接到相同的起始节点和结束节点，并且它们之间没有相互影响。

每个分支中都存在着独立的元件（如电阻、灯泡等）。

2.3 并联电路中电流和电压的关系在并联电路中，不同分支上的元件具有相同的总体供应电压。

这意味着，在并联连接处，各个分支上的元件所连接到的相同节点上会有相同大小的供应电压。

然而，在不同分支上，由于每个元件具有不同的阻抗（如不同大小的电阻），因此流过每个元件的电流会有所不同。

在并联连接处，各个分支中的电流将汇合形成总电流，也就是说总电流等于各个分支中的电流之和。

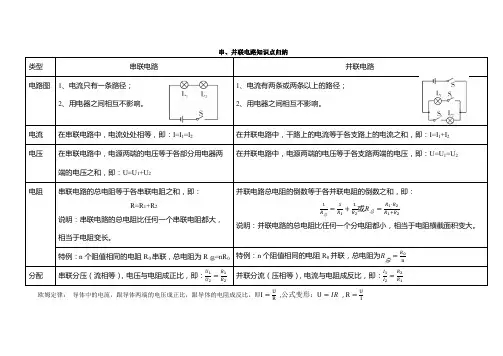
串、并联电路中的电阻关系（基础）责编：冯保国【学习目标】1.能根据欧姆定律以及电路的特点，得出串、并联电路中电阻的关系。

2.理解欧姆定律，能运用欧姆定律进行简单的计算。

【要点梳理】要点一、等效电阻在电路中，如果一个电阻的效果和几个电阻在同一电路中的效果相同，可以认为这个电阻是几个电阻的等效电阻。

这个概念可以结合“合力与分力的关系”对照理解。

》如果电源电压相同，在图1和图2中电流表示数相同，可以认为R为R1和R2串联后的等效电阻，也称总电阻。

要点诠释：电阻在电路中的作用即对电流的阻碍作用。

这里的“等效”可以理解为在同一个电路中，即电源电压相同，电阻对电流的阻碍作用相同，电路中的电流大小相同。

要点二、串联电路中的电阻关系在图1中，因为R1和R2串联，因此通过它们的电流相同，设R1两端电压为U1，R2两端电压为U2，则有:1212111222I I IU U UU I RU I R===+==在图2中有：U IR=综合以上推导，有：1122IR I R I R=+；因此可以得到有串联电路总电阻和分电阻的关系：12R R R=+要点诠释：（1）导体串联，相当于增加了导体的长度，因此，串联导体的总电阻大于任何一个串联导体的电阻，总电阻等于各串联导体电阻之和，即12......nR R R R=+++。

&（2）如果用n个阻值均为R0的导体串联，则总电阻为R nR=。

要点三、并联电路中的电阻关系如图3、图4所示,R1和R2并联。

两个图中电流表示数相同，说明R和R1、R2并联的效果相同，可以认为R是其等效电阻。

在图3中，有1212111222=I I IU U UUIRUIR=+===在图4中，有:UIR=综合以上推导，有1212U UUR R R=+;即：12111R R R=+, 1212R RRR R=+·要点诠释：（1）导体并联，相当于增大了导体的横截面积，因此，并联导体的总电阻小于任何一个并联导体的电阻，总电阻的倒数等于各并联导体电阻的倒数之和，即121111.....nR R R R=+++。

四、并联电路中的电阻关系 五、欧姆定律的应用【学习要求】1 •知道什么是并联电路，能区别串联电路和并联电路。

2 .理解并联电路中各个导体的电流、电压、电阻跟电路的总电流、总电压、总电阻的关系。

3 •能运用欧姆定律求解并联电路的常见问题。

【知识讲解】 一、知识回顾1 •电路的联接有两种基本方式，一种是将元件逐个顺次地联接起来，叫做串联；另一种是将元件并列地连接起来， 叫做并联。

2 •串联电路电流无分支，并联电路中电流要分成两条或多条支路；串联电路可以同时控制，而并联电路可以分别控 制。

二、并联电路1 •问题的提出修电子仪器时，需要一个 的电阻组合起来代替？并联电阻的知识，可以帮助我们解决这类问题，也可以用几个阻值大一些的电阻组合起来形成一个总电阻来代替 一个阻值小的电阻。

2 •电阻的并联，把几个电阻并列地连接起来叫电阻的并联.如图我们学过并联电路的部分特点11 , _乩， I ~~亠 卜一卍卜 ---- Ua.并联电路干路中的电流等于各支路中的电流之和I = I 1 + I 2 b.并联电路里，各支路两端的电压相等 U = U 1 = U 2禾U 用上面并联电路中两个特点和欧姆定律，可以推导岀电阻并联后的总电阻与各个电阻之间的关系干路上的电流1R ，其中R为并联电路的总电阻U R 2故丄丄丄 R R]R ?3 •结论：这表明并联电路的总电阻的倒数，等于各并联电阻的倒数之和。

提岀的问题，现在可以知道了，把两只 10千欧的电阻并联起来就可以得到 5千欧的电阻了。

从决定电阻大小的因素来看，把几个电阻并联起来，总电阻比任何一个电阻都小，这相当于增大了导体的横截面积。

111三、对一一一的理解R Ri R 2①并联电路的总电阻比任何一个分电阻都小， 即: R V R 1，R V R 2，可以理解为电阻并联时，相当于增加了导体的横截面积，而横截面积越大，导体电阻越小；例如，一个6欧和一个3欧的电阻并联后，总电阻为 2欧，小于任何一个并联电如图所示：设并联电阻的阻值为R 1、R 2,并联后的总电阻为 R ，由于各支路的电阻 R 1、R 2两端的电压都等于U ，根据欧姆定律，可求得: 支路电流“ U 1和125千欧的电阻，而手头只有 20千欧、10千欧等多个电阻，那么可以把 20千欧或10千欧U R 2阻。

假设电源电压一样，在图 1 和图 2 中电流表示数一样，可以认为R 为 R 和 R 串联后的等效电阻，也称 1 2 总电阻。

串、并联电路中的电阻关系〔根底〕责编：冯保国【学习目标】 1. 能依据欧姆定律以及电路的特点，得出串、并联电路中电阻的关系。

2. 理解欧姆定律，能运用欧姆定律进展简洁的计算。

【要点梳理】要点一、等效电阻在电路中，假设一个电阻的效果和几个电阻在同一电路中的效果一样，可以认为这个电阻是几个电阻的等效电阻。

这个概念可以结合“合力与分力的关系”比照理解。

要点诠释：电阻在电路中的作用即对电流的阻碍作用。

这里的“等效”可以理解为在同一个电路中，即电源电压一样，电阻对电流的阻碍作用一样，电路中的电流大小一样。

要点二、串联电路中的电阻关系在图 1 中，由于R 和R 串联，因此通过它们的电流一样，设R 两端电压为U ，R 两端电压为U ，12I = I = I 121122则有:U = U + U 12在图 2 中有：U = IR综合以上推导，有：IR = I R + I R ； U = I R 1 1 1 U = I R1 12 222 2要点诠释：R = R + R12（1） 导体串联，相当于增加了导体的长度，因此，串联导体的总电阻大于任何一个串联导体的电阻，总电阻等于各串联导体电阻之和，即R = R + R 1 2+ ...... + R 。

n（2） 假设用n 个阻值均为R 0的导体串联，则总电阻为R = nR 。

要点三、并联电路中的电阻关系如图 3、图 4 所示,R 1 和R 2 并联。

两个图中电流表示数一样，说明R 和R 1、R 2 并联的效果一样，可以认为R 是其等效电阻。

因此可以得到有串联电路总电阻和分电阻的关系：〔3〕不管是串联还是并联电路中，某个电阻的阻值增大，电路的总电阻都是增大；假设电路中电阻的个数增多，则串联电路的总电阻增大，而并联电路的总电阻减小。

要点四、串、并联电路中电阻规律的应用1.串联电路中，电阻阻值之比等于电阻两端电压之比。

并联电流的关系并联电流的关系概述在电路中，有两种主要的连接方式：串联和并联。

并联电路是指多个电器或元件通过共享两个连接点来连接的电路。

在这种情况下，电流将分流通过每个并联元件。

本文将重点讨论并联电路中电流的关系。

并联电路在一个并联电路中，电流可以沿着多个路径流动。

由于并联电路中的电流不会相互干扰，因此通过每个并联元件的电流都是相同的。

这是并联电流的基本关系。

元件电流的计算当我们需要计算并联电路中各个元件的电流时，我们可以利用以下公式进行计算：总电流 = 电流1 + 电流2 + 电流3 + ...即并联电路中的总电流等于各个并联元件的电流之和。

电阻的并联电流计算在并联电路中，若有多个电阻连接在一起，并且它们之间没有其他元件干扰，那么它们的电流之间是相同的。

也就是说，多个并联电阻的电流相等。

电容的并联电流计算在并联电路中，多个电容并联连接时，它们的电流也是相等的。

电感的并联电流计算与电阻和电容类似，多个并联的电感元件的电流也相等。

总结在并联电路中，电流通过每个并联元件的大小相等。

这是由于并联电路的特性决定的。

无论是电阻、电容还是电感元件，它们在并联电路中的电流都是相同的。

了解并联电流的关系对于电路分析和设计非常重要，因为它能够帮助我们有效地计算电路中各个元件的电流。

示例计算为了更好地理解并联电流的计算方法，我们可以举一个简单的示例来说明。

假设有一个并联电路，其中有两个电阻元件，电阻值分别为R1和R2。

假设总电流为I，我们需要计算通过每个电阻的电流。

根据前面提到的公式，我们知道总电流等于各个并联元件的电流之和，即：I = I1 + I2又根据电阻的欧姆定律，电流与电阻之间的关系为：I = V / R其中V为电压，R为电阻。

由于并联电路中的电压相等，所以我们可以得到：V = V1 = V2将上述公式代入前一公式，我们可以得到：I = V1 / R1 + V2 / R2再将V1和V2代入为V，我们可以得到：I = V / R1 + V / R2继续化简，我们得到：I = V * (1/R1 + 1/R2)由此可见，通过每个电阻的电流之和等于总电流，而每个电阻的电流都与其电阻值的倒数成比例。

串并联电路、电压表、电流表编稿：xxx 审稿：xxx【学习目标】1．掌握串、并联电路的特点，并能熟练地识别电路中元件之间的连接关系，能够运用串并联的规律理解计算电表的改装。

2．识别电路中各元件的连接关系，画出简明的等效电路图，以及电流表、电压表、电容等对电路的影响。

【要点梳理】要点一、串联电路的特点和性质1．基本特点（1）在串联电路中，各处的电流相等，即123nI I I I I=====．（2）串联电路的总电压等于各部分电压之和，即123nU U U U U=++++.（3）串联电路的等效总电阻为各电阻值之和，即123nR R R R R=++++．2．性质（1）串联电路的电压分配关系：各个电阻两端的电压跟它们的阻值成正比，即312123.nnU UU UIR R R R=====或123123=U:U:U R:R:R.其中：111232212333123=++=++=++RU U,R R RRU U,R R RRU U.R R R（2）串联电路的功率分配关系：各个电阻消耗的功率跟它们的阻值成正比，即2312123.nnP PP PIR R R R=====或：123123=P:P:P R:R:R要点诠释：○1n个相同的电阻R串联后的总电阻=R nR总.○2串联电路的总电阻大于其中任一部分电路电阻。

○3串联电路的每个电阻R都分担了一部分电压，串联电路的这种作用叫作分压作用，起分压作用的电阻叫作分压电阻。

要点二、并联电路的特点和性质1．基本特点（1）并联电路中各支路的电压相等，即123nU U U U U=====．（2）并联电路的总电流等于各支路电流之和，即123nI I I I I=++++．（3）并联电路的等效总电阻R与各支路的电阻123,nR R R R、、的关系是：12311111nR R R R R=++++．2．性质（1）并联电路的电流分配关系：各支路电流跟它们的电阻成反比，即112233n nI R I R I R I R U=====.或：123123111=I:I:I::R R R.（2）并联电路的功率分配关系：各支路电阻消耗的功率跟它们的电阻成反比，即2112233n nP R P R P R P R U=====.或：123123111=P:P:P::R R R.要点诠释：○1n个相等的电阻R并联后的总电阻=RRn总．○2并联电路的总电阻小于其中最小的电阻。

串联和并联电路讲解串联和并联电路讲解【一】我们用电器所能承受的电压，总是等于电源电压，而且总大于单个用电器允许通过的电压。

这是因为在串联电路中各用电器两端的电压等于电源电压，这样就会使得流经每个用电器的电流都相同，即用电器两端电压不会因为用电器数量增多而有明显变化，所以称串联电路的总电压等于电源电压。

①干路、支路是从电源的正极到负极。

②并联电路中各元件两端电压相等，而支路电流只与各支路电阻成反比，与干路电流无关，所以并联电路中总电流等于各支路电流之和。

③并联电路中各支路的电流，可以相互抵消，故支路电流只等于各支路电阻之积。

④由于各支路电阻不等，分流作用可以相互抵消，所以总电流也就等于各支路电流之积。

⑤串联电路中，由于电流处处相等，所以总电阻较大的电路，可以分配较小的电流，从而实现分压，提高电路的功率因素。

当然，若干路串联的总电阻很小，可以分配很大的电流，但它们的电流强度却可能相差悬殊，那么根据分流原理，其中某一路就要减小电流强度，造成该路的总电流小于其他几路，那么整个电路的电流就必定较小。

⑥根据欧姆定律：导体的电阻与导体两端的电压成反比，与导体的电流强度成正比，与导体的横截面积成反比。

当用电器串联后形成总电阻时，导体的电阻较大，故产生的总电流就越大。

所谓的“并联”电路，是指电流是从电源的正极出发，最终回到电源的负极。

当电流从一条路径流入后，会顺着另一条路径流出，以此类推。

那么假设三个人站在三个不同的位置，第一个人将电灯关闭，而第二个人又将电灯打开，那么从任意一个人开始，通过这三个电灯的电流都是0。

这是一种特殊的情况。

在正常情况下，当三盏灯串联起来的时候，它们所共用的电压一般为总电压的一半，即，并联电路中总电流等于各支路电流之和。

例如当每个人把电灯打开时，三盏灯的电压为12V，通过三盏灯的电流强度为0。

则每盏灯的电流强度为0。

14V，由于每盏灯的电阻不同，故而这些电流分别加在了三盏灯上。

因此，在每盏灯的两端会有电压，其值相等。

电路中通过各个并联电阻两端电压的关系标题：深度解析电路中并联电阻两端电压的关系在电路中，我们经常会遇到并联电阻的情况。

并联电阻是指多个电阻以平行的方式连接在一起，它们的两端电压之间的关系是一个非常重要的物理现象。

本文将从简单到深入地探讨并联电阻两端电压的关系，旨在帮助读者更深入地理解这一重要概念。

1. 并联电阻的基本概念我们需要了解并联电阻的基本概念。

当多个电阻以平行的方式连接在一起时，它们的两端电压相同，但通过每个电阻的电流可能不同。

这是因为并联电路中，电流可以选择不同的路径通过不同的电阻，而电压是相同的。

2. 电流分配规律在并联电路中，电流会按照各个电阻的电阻值进行分配。

根据欧姆定律，电流与电阻成反比，因此电阻值越小的电阻将获得更大的电流。

这也就意味着，电流将优先通过电阻值小的电阻。

我们可以得出结论：在并联电路中，电流会按照电阻值的倒数来分配。

3. 电压分配规律接下来，我们来探讨并联电阻两端电压之间的关系。

根据基尔霍夫电压定律，任何一个闭合回路内的电动势之和等于回路内电阻两端电压之和。

在并联电路中，各个电阻的两端电压相同，且等于整个回路的电压。

4. 个人观点和理解对于并联电阻两端电压的关系，我个人的理解是：并联电路中，电阻值越小的电阻将获得更大的电流，因此其两端电压可能会受到更大的影响。

而电阻值大的电阻将获得相对较小的电流，其两端电压可能会受到相对较小的影响。

这种电流和电压的分配规律，是并联电路中非常重要却又常常被忽视的一点。

通过对并联电阻两端电压的深入探讨，我们更深入地理解了这一重要概念。

在实际应用中，对并联电阻两端电压的准确理解，将有助于我们更好地设计和分析电路，从而实现更优秀的电路性能。

在本文中，我们从基本概念、电流分配规律、电压分配规律和个人观点等方面对并联电阻两端电压的关系进行了深入探讨，希望对读者有所帮助。

（注：本文所提供的主题词“电路中通过各个并联电阻两端电压的关系”已经在文章中多次提及。