串,并联在电路中的等效电阻

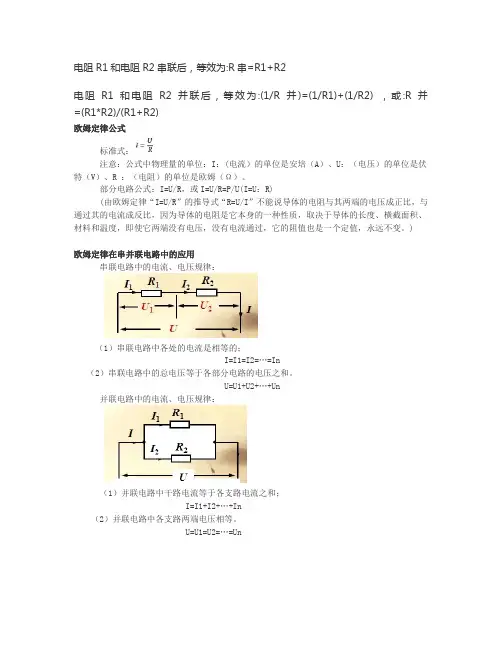
电阻R1和电阻R2串联后，等效为:R串=R1+R2
电阻R1和电阻R2并联后，等效为:(1/R并)=(1/R1)+(1/R2) ，或:R并=(R1*R2)/(R1+R2)
欧姆定律公式
标准式：
注意：公式中物理量的单位：I：(电流）的单位是安培（A）、U：（电压）的单位是伏特（V）、R ：（电阻）的单位是欧姆（Ω）。

部分电路公式：I=U/R，或I=U/R=P/U(I=U：R)
(由欧姆定律“I=U/R”的推导式“R=U/I”不能说导体的电阻与其两端的电压成正比，与通过其的电流成反比，因为导体的电阻是它本身的一种性质，取决于导体的长度、横截面积、材料和温度，即使它两端没有电压，没有电流通过，它的阻值也是一个定值，永远不变。

)
欧姆定律在串并联电路中的应用
串联电路中的电流、电压规律：
（1）串联电路中各处的电流是相等的；
I=I1=I2= (I)
（2）串联电路中的总电压等于各部分电路的电压之和。

U=U1+U2+…+Un
并联电路中的电流、电压规律：
（1）并联电路中干路电流等于各支路电流之和；
I=I1+I2+ (I)
（2）并联电路中各支路两端电压相等。

U=U1=U2=…=Un。

串并联电路中的等效电阻计算公式串联电路中的等效电阻计算公式：在串联电路中，多个电阻连在一起，电流依次通过每个电阻。

电阻的总和即为等效电阻，用来表示整个电路的总阻力。

在串联电路中，电流恒定，即通过每个电阻的电流相等。

根据欧姆定律，电阻的电压与电流成正比。

因此，可以通过串联电阻的电压和电流来计算等效电阻。

设有 n 个串联电阻，每个电阻的阻值分别为 R₁, R₂, ..., Rₙ，则串联电路的等效电阻 R_eq 的计算公式为：R_eq = R₁ + R₂ + ... + Rₙ并联电路中的等效电阻计算公式：在并联电路中，多个电阻分别连接在电路的不同分支上，电压相同，电流分成多个支路。

并联电路的等效电阻用来表示整个电路的总阻力。

在并联电路中，电压恒定，即每个电路分支的电压相等。

根据欧姆定律，电流与电阻成反比。

因此，可以通过并联电阻的电流和电压来计算等效电阻。

设有 n 个并联电阻，每个电阻的阻值分别为 R₁, R₂, ..., Rₙ，则并联电路的等效电阻 R_eq 的计算公式为：1/R_eq = 1/R₁ + 1/R₂ + ... + 1/Rₙ等效电阻的实际应用：1.简化复杂电路：等效电阻可以将复杂的电路简化为一个电阻，方便计算和分析整个电路的特性。

2.增加电路的性能：通过调整等效电阻的值，可以改变电路的总阻力，从而实现对电路性能的控制。

3.电阻的替代：等效电阻可以用来替代一组电阻，使得电路更为简单且易于设计。

4.电阻的合并：等效电阻可以将多个电阻合并为一个，减少电路元件的数量和占用空间。

总结：串联电路的等效电阻可通过将每个电阻的阻值相加得到，而并联电路的等效电阻可通过将每个电阻的倒数相加，再取倒数得到。

等效电阻的计算公式是在电路分析和计算中的基础，能够简化复杂电路的分析和设计过程，同时也能够优化电路的性能。

串并联电路中电阻的科学方法
在串并联电路中，电阻的计算可以通过以下几种科学方法：
1. 等效替代法：这种方法可以应用于串并联电路中。

在串联电路中，所有电阻可以用一个等效电阻替代；在并联电路中，所有电阻也可以用一个等效电阻替代。

这个等效电阻就是电路的总电阻。

2. 利用欧姆定律：对于串联电路，利用欧姆定律可得IR=IR1+IR2，已知串联电路中电流处处相等，约掉I，则R=R1+R2；对于并联电路，利用欧姆
定律可得U/R=U/R1+U/R2，已知并联电路中各支路电压都等于电源电压，约掉U，则1/R=1/R1+1/R2。

3. 观察法：在串联电路中，电阻越串越大，相当于增加电阻的长度；在并联电路中，电阻越并越小，相当于增加电阻的横截面积。

请注意，以上信息仅供参考，如需了解更多串并联电路中电阻的科学方法，建议咨询物理专业人士或查阅物理书籍。

电阻的串并联与电路的等效电阻电路中的电阻是一种常见的元件，它用于控制电流的流动。

在电路设计和分析中，了解电阻的串并联以及电路的等效电阻是非常重要的。

本文将介绍电阻的串并联的概念，并探讨如何计算电路的等效电阻。

一、电阻的串联在电路中，当电阻按照一定的顺序连接在一起时，我们称之为电阻的串联。

串联的电阻会形成一个总电阻，总电阻等于各电阻之和。

例如，如果我们有三个电阻R1、R2和R3串联在一起，它们的阻值分别为R1，R2和R3。

那么总电阻RT可以通过下面的公式计算：RT = R1 + R2 + R3需要注意的是，电阻的串联不仅适用于三个电阻，也可以适用于任意数量的电阻。

总电阻等于每个电阻之间的阻值相加。

二、电阻的并联与电阻的串联相反，电阻的并联是指将多个电阻按照平行连接的方式连接在一起。

并联的电阻会形成一个总电阻，总电阻等于各电阻阻值的倒数之和的倒数。

假设我们有三个电阻R1、R2和R3并联在一起，它们的阻值分别为R1，R2和R3。

那么总电阻RT可以通过下面的公式计算：1/RT = 1/R1 + 1/R2 + 1/R3同样地，电阻的并联也适用于任意数量的电阻。

总电阻的倒数等于每个电阻的倒数之和的倒数。

三、电路的等效电阻在电路分析中，我们经常需要将一个复杂的电路简化为一个等效电阻。

等效电阻是一个能够代替原电路，使得原电路和等效电阻在外部电路中起到相同作用的电阻。

当电路中的电阻既有串联又有并联时，我们可以通过计算来求解电路的等效电阻。

首先，将电路中的电阻按照串联和并联的方式进行分组，然后计算每组的等效电阻。

最后，将这些等效电阻按照串联或并联的方式相连，就得到了整个电路的等效电阻。

举个例子，假设我们有一个电路，其中有两个电阻R1和R2串联在一起，再与一个电阻R3并联。

我们可以按照下面的步骤计算等效电阻：1. 先计算R1和R2的串联电阻，得到R12。

2. 再将R12与R3的并联电阻计算，得到整个电路的等效电阻RT。

串联电阻与并联电阻的等效电阻电阻是电路中常见的元件之一，它具有阻碍电流流动的作用。

在电路中，常常会遇到串联电阻和并联电阻这两种情况。

本文将探讨串联电阻和并联电阻的等效电阻概念及其计算方法。

一、串联电阻的等效电阻串联电阻指的是将多个电阻依次连接在一起，电流按顺序通过每个电阻。

串联电阻的等效电阻是指将这些串联电阻简化为一个等效电阻，与串联电阻组合相连的电路的性质相同。

计算串联电阻的等效电阻需要使用串联电阻的计算公式，即等效电阻为各个电阻之和，即R_eq = R₁ + R₂ + ... + Rₙ，其中R_eq为等效电阻，R₁、R₂、...、Rₙ分别为串联电阻的各个电阻值。

例如，有三个串联电阻，分别为10欧姆、20欧姆和30欧姆，求它们的等效电阻。

根据串联电阻的计算公式可知，等效电阻R_eq = 10欧姆 + 20欧姆 + 30欧姆 = 60欧姆。

二、并联电阻的等效电阻并联电阻指的是将多个电阻同时连接在电路中，电流可以分别通过每个电阻。

并联电阻的等效电阻是指将这些并联电阻简化为一个等效电阻，与并联电阻组合相连的电路的性质相同。

计算并联电阻的等效电阻需要使用并联电阻的计算公式，即等效电阻为各个电阻的倒数之和的倒数，即1/R_eq = 1/R₁ + 1/R₂ + ... + 1/Rₙ，然后取其倒数。

例如，有三个并联电阻，分别为10欧姆、20欧姆和30欧姆，求它们的等效电阻。

根据并联电阻的计算公式可知，1/R_eq = 1/10欧姆 +1/20欧姆 + 1/30欧姆= 0.1 + 0.05 + 0.033 ≈ 0.183，再将其倒数，即R_eq = 1 / 0.183 ≈ 5.46欧姆。

三、串联电阻和并联电阻的等效电阻应用串联电阻和并联电阻的等效电阻概念在电路设计和分析中具有广泛的应用。

通过求解等效电阻，可以简化电路，方便后续计算和分析。

在实际应用中，我们经常需要根据电路的需求来选择串联电阻和并联电阻的数值，以达到所期望的电路性能。

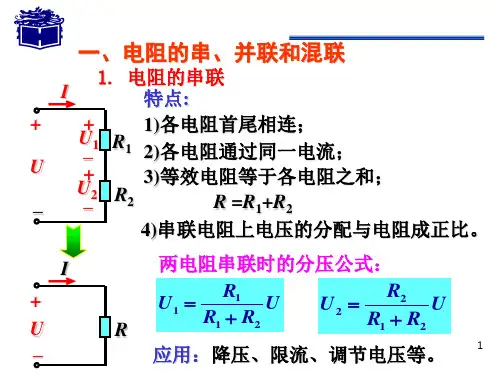
串、并联电路中的等效电阻及计算公式串、并联电路中的等效电阻学习目标要求：1．知道串、并联电路中电流、电压特点。

2．理解串、并联电路的等效电阻。

3．会计算简单串、并联电路中的电流、电压和电阻。

4．理解欧姆定律在串、并联电路中的应用。

5．会运用串、并联电路知识分析解决简单的串、并联电路问题。

中考常考内容：1．串、并联电路的特点。

2．串联电路的分压作用，并联电路的分流作用。

3．串、并联电路的计算。

知识要点：1．串联电路的特点（1）串联电路电流的特点：由于在串联电路中，电流只有一条路径，因此，各处的电流均相等，即；因此，在对串联电路的分析和计算中，抓住通过各段导体的电流相等这个条件，在不同导体间架起一座桥梁，是解题的一条捷径。

（2）由于各处的电流都相等，根据公式，可以得到，在串联电路中，电阻大的导体，它两端的电压也大，电压的分配与导体的电阻成正比，因此，导体串联具有分压作用。

串联电路的总电压等于各串联导体两端电压之和，即。

（3）导体串联，相当于增加了导体的长度，因此，串联导体的总电阻大于任何一个串联导体的电阻，总电阻等于各串联导体电阻之和，即。

如果用个阻值均为的导体串联，则总电阻。

2．并联电路的特点（1）并联电路电压的特点：由于在并联电路中，各支路两端分别相接且又分别接入电路中相同的两点之间，所以各支路两端的电压都相等，即。

因此，在电路的分析和计算中，抓住各并联导体两端的电压相同这个条件，在不同导体间架起一座桥梁，是解题的一条捷径。

（2）由于各支路两端的电压都相等，根据公式，可得到，在并联电路中，电阻大的导体，通过它的电流小，电流的分配与导体的电阻成反比，因此，导体并联具有分流作用。

并联电路的总电流等于各支路的电流之和，即。

（3）导体并联，相当于增大了导体的横截面积，因此，并联导体的总电阻小于任何一个并联导体的电阻，总电阻的倒数等于各并联导体电阻的倒数之和，即。

如果用个阻值均为的导体并联，则总电阻。

（4）并联电路各支路互不影响，即当一条支路中的电阻发生改变时，只会导致本支路中的电流发生改变，而对其他支路中的各物理量均无影响（因为其他支路两端的电压和电阻均未改变），但是干路中的电流会随可变支路中电流的增大而增大，随着可变支路中电流的减小而减小，而且增大和减小的数值相同。

电阻的串并联与电路的等效电阻电阻的串联和并联是电路中常见的连接方式，它们在电路中起着重要的作用。

本文将介绍电阻的串并联原理及其对电路的等效电阻的影响。

1. 串联电阻的原理电阻的串联是指将多个电阻按照一定的顺序连接在一起，电流依次通过每个电阻。

串联电阻的等效电阻可通过将所有电阻的阻值相加得到。

以两个串联电阻为例，电阻R1和R2串联连接，其等效电阻可表示为：RT = R1 + R2如果有更多的电阻进行串联连接，可以按照相同的原理进行计算，将所有电阻的阻值相加。

2. 并联电阻的原理电阻的并联是指将多个电阻同时连接在电路中，它们的两端相连。

并联电阻的等效电阻可通过将所有电阻的导纳（即电导的倒数）相加，再取其倒数得到。

以两个并联电阻为例，电阻R1和R2并联连接，其等效电阻可表示为：1/RT = 1/R1 + 1/R2如果有更多的电阻进行并联连接，可以按照相同的原理进行计算，将所有电阻的导纳相加后再取其倒数。

3. 串并联的混合情况在实际电路中，常常会出现串联和并联的混合情况。

此时，可以先将所有的串联电阻进行合并，再将合并后的串联电阻与并联电阻进行并联。

以一个示例电路为例，该电路中有两个串联电阻R1和R2，和一个并联电阻R3。

首先将R1和R2合并为一个等效电阻RT1，计算公式为RT1 = R1 + R2。

然后将RT1和R3进行并联，计算公式为：1/RT = 1/RT1 + 1/R3得到最终的等效电阻RT。

综上所述，电阻的串并联可以通过简单的计算得到等效电阻。

在实际的电路设计和分析中，等效电阻的求解可以简化计算，并帮助我们更好地理解电路的特性。

总结：电阻的串联和并联是电路中常见的连接方式。

串联电阻的等效电阻为各个电阻的阻值之和，而并联电阻的等效电阻为各个电阻导纳之和的倒数。

在实际电路中，常常会有串并联的混合情况，我们可以先合并串联电阻，再与并联电阻进行并联计算。

通过等效电阻的求解，我们可以简化电路计算，并更好地理解电路的行为与特性。

电路中的电阻串联和并联电阻的等效问题在电路中，电阻是一个重要的元件。

在电路设计和分析中，经常会遇到电阻串联和并联电阻的等效问题。

本文将详细讨论电路中电阻串联和并联的概念、计算方法以及等效电阻的计算。

1. 电阻串联的概念和计算方法电阻串联是指将两个或多个电阻按顺序连接在一起的方式。

当电阻串联时，电流依次通过每个电阻。

电阻串联的总电阻可以通过将每个电阻的阻值相加来计算。

假设有两个电阻R1和R2，它们串联在一起，总电阻记为RT。

那么，总电阻的计算公式如下：RT = R1 + R22. 电阻并联的概念和计算方法电阻并联是指将两个或多个电阻同时连接在电路中的方式。

当电阻并联时，电流会分流经过各个电阻。

电阻并联的总电阻可以通过将每个电阻的倒数相加后再取倒数来计算。

假设有两个电阻R1和R2，它们并联在一起，总电阻记为RP。

那么，总电阻的计算公式如下：1/RP = 1/R1 + 1/R2电阻串联和并联的概念和计算方法可以扩展到多个电阻的情况。

例如，对于三个电阻R1、R2和R3的串联电路，总电阻的计算公式为：RT = R1 + R2 + R3对于三个电阻R1、R2和R3的并联电路，总电阻的计算公式为：1/RP = 1/R1 + 1/R2 + 1/R33. 电阻串联和并联的等效问题在电路中，经常需要求解电阻串联和并联电阻的等效问题。

等效问题是指将一个复杂的电路转化为一个简化的电路，该简化电路具有相同的电流电压特性。

电阻串联和并联的等效问题可以通过计算总电阻来实现。

对于电阻串联，可以将多个串联的电阻替换为一个等效电阻。

等效电阻的值与串联的电阻之和相等。

通过使用等效电阻，可以简化电路的分析和计算。

对于电阻并联，可以将多个并联的电阻替换为一个等效电阻。

等效电阻的值可以通过并联电阻的倒数之和再取倒数来计算。

同样地，使用等效电阻可以简化电路的分析和计算。

4. 实例分析现在我们来看一个具体的例子，以帮助理解电阻串联和并联的计算。

等效电路及等效电阻的计算等效电路是为了简化复杂的电路，使其具有相同的电流电压特性的简化电路。

等效电阻是指可以用一个单一的电阻来替代电路中所有的电阻，以实现相同的电流和电压特性。

计算等效电路和等效电阻可以通过以下几种方法来实现：串联电阻、并联电阻、星型变三角形变换及三角形变星型变换。

1.串联电阻：当电路中存在多个串联电阻时，它们的等效电阻可以通过简单地将它们相加来计算。

即：Req = R1 + R2 + R3 + ...2.并联电阻：当电路中存在多个并联电阻时，它们的等效电阻可以通过使用并联电阻的公式来计算。

即：1/Req = 1/R1 + 1/R2 + 1/R3 + ...然后，将公式两边取倒数，得到：Req = 1/(1/R1 + 1/R2 + 1/R3 + ...)3.星型变三角形变换：当电路中存在三角形电阻网络时，可以通过星型变换来计算其等效电阻。

对于三角形电阻网络，可以将其转换为等效的星型电阻网络。

在星型电阻网络中，三个电阻分别与另一电阻的三个角点相连。

此时，等效电阻的计算公式为：Req = R1*R2/(R1+R2+R3)4.三角形变星型变换：当电路中存在星型电阻网络时，可以通过三角形变换来计算其等效电阻。

对于星型电阻网络，可以将其转换为等效的三角形电阻网络。

在三角形电阻网络中，三个电阻分别与另一电阻的三个角点相连。

此时，等效电阻的计算公式为：1/Req = 1/R1 + 1/R2 + 1/R3然后，将公式两边取倒数，得到：Req = 1/(1/R1 + 1/R2 + 1/R3)以上是计算等效电路及等效电阻的基本方法，可以根据不同的电路情况选择合适的方法来计算。

需要注意的是，在实际应用中，还有其他的一些复杂电路计算方法，例如电阻网络的星-箭头变换、戴维南等效电源法等。

串、并联电路的等效电阻一、电路基本概念1.电路：电路是由电源、导线和用电器组成，能使电流流通的系统。

2.串联电路：电路中各元件首尾顺次连接，电流只有一条路径的电路。

3.并联电路：电路中各元件并列连接，电流有多条路径的电路。

二、电阻的性质1.电阻：电阻是电路中对电流流动的阻碍作用，单位为欧姆（Ω）。

2.电阻的决定因素：电阻大小取决于导体的材料、长度、横截面积和温度。

3.电阻的串联：串联电路中，总电阻等于各分电阻之和。

4.电阻的并联：并联电路中，总电阻的倒数等于各分电阻倒数之和。

三、串并联电路的等效电阻1.等效电阻：等效电阻是将复杂电路中的多个电阻简化为一个电阻，使得电路的电压、电流分布不变。

2.串联电路的等效电阻：串联电路的等效电阻等于各分电阻之和。

3.并联电路的等效电阻：并联电路的等效电阻的倒数等于各分电阻倒数之和。

4.等效电阻的计算：根据电路中电阻的串并联关系，运用电阻的性质和公式计算等效电阻。

四、串并联电路的电压、电流关系1.串联电路：串联电路中，各处的电流相等；总电压等于各分电压之和。

2.并联电路：并联电路中，各支路的电压相等；干路电流等于各支路电流之和。

3.电路分析：运用串并联电路的等效电阻概念，简化电路分析，便于计算电路中的电压、电流。

4.电路设计：根据实际需求，设计串并联电路，选取合适的电阻，满足电路性能要求。

5.电子设备：串并联电路在电子设备中广泛应用，如电源、信号传输、滤波等电路。

六、注意事项1.理解串并联电路的等效电阻概念，区分串联和并联电路的等效电阻计算方法。

2.在计算等效电阻时，注意电阻的单位，确保数值准确。

3.掌握串并联电路的电压、电流关系，以便在实际应用中正确分析电路。

综上所述，串、并联电路的等效电阻是电路分析的重要知识点，掌握其原理和计算方法，有助于更好地理解和应用电路。

习题及方法：一个电阻值为10Ω的电阻R1与一个电阻值为5Ω的电阻R2串联，求该串联电路的总电阻。

根据串联电路的等效电阻性质，总电阻R等于各分电阻之和，所以：R = R1 + R2= 10Ω + 5Ω答案：该串联电路的总电阻为15Ω。

电阻的串联和并联等效变换1.电阻串联(1)电流：各电阻顺序连接，流过同一电流(2)电压：总电压等于各串联电阻的电压之代数和nk u u u u +⋅⋅⋅++⋅⋅⋅+=1+_R 1R n +_u k i+_u 1+_u n uR k R 2+_u 2i 1i 2由欧姆定律串联电路的总电阻等于各分电阻之和iR R i R i R i R u n n k )(11++=++++= ∑==++++==nk k n k R R R R i uR 11 eq R eq i +_u(3)等效电阻等效nku u u u +⋅⋅⋅++⋅⋅⋅+=1+_R 1R n +_u k i+_u 1+_u n u R kR 2+_u 2kR >(4)电压分配i R u k k =分压公式电压与电阻成正比21eq2eq121R R u R R uR R u u ==R eq i +_u等效u u R R R uR k k <==eqeq +_R 1R n +_u k i+_u 1+_u n u R kR 2+_u 2(5)功率eq eq eq p p R R i R p k k k <==2各电阻消耗的功率与电阻大小成正比2121R R p p =总功率等于各串联电阻消耗功率的和()n n k PP i R R R i R p ++=++++== 1212eq eq R eqi +_u等效+_R 1R n +_u ki +_u 1+_u nu R k R 2+_u 22.电阻并联(1)电压：各电阻两端为同一电压(2)电流：总电流等于各并联电阻的电流之代数和nk i i i i +⋅⋅⋅++⋅⋅⋅+=1i i nR 1R kR n+u i 1i k _R 2i 2并联电路的等效电导等于并联的各电导之和等效R eqi +_u(3)等效电阻∑==+++==nk k n G G G G u iG 121 eq )(11n n G G G u uG uG uG i +⋅⋅⋅++=+⋅⋅⋅++=22kR G R <=eqeq 1nk i i i i +⋅⋅⋅++⋅⋅⋅+=1i i n R 1R kR n+u i 1i k _R 2i 2kG >(4)电流分配电流与电导成正比eqeq G G R u R u i i kk k ==//i G G i kk eq=分流公式21eq2eq 121G G i G G iG G i i ==等效R eqi +_ui i n R 1R kR n+u i 1i k _R 2i 2(5)功率eqeq eqp p G G u G p k k k <==2各电阻消耗的功率与电阻大小成反比122121R R G G p p ==总功率等于各并联电阻消耗功率的和()n n k PP u G G G u G p ++=++++== 1212eq eq 等效R eqi +_uii n R 1R kR n+u i 1i k _R 2i 2有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）3.电阻的串并联电路中有电阻的串联，又有电阻的并联，这种连接方式称电阻的串并联。

电阻电路的串并联等效电阻计算电阻电路是电子电路中常见的一种电路形式。

在实际的电路中，电阻器经常会被串联或并联起来，形成串联电路或并联电路。

了解如何计算串并联电路的等效电阻对于解决实际问题以及设计电路非常重要。

一、串联电路的等效电阻计算串联电路是指将电阻器顺序连接在一起，电流从一个电阻器流过，再流向下一个电阻器。

在串联电路中，电阻器的总电阻等于各个电阻器的电阻之和。

设有n个串联的电阻器R1，R2，…，Rn，它们的电阻分别为R1，R2，…，Rn，则电阻器的总电阻R为：R = R1 + R2 + … + Rn二、并联电路的等效电阻计算并联电路是指将电阻器的一个端头连接在一起，另一个端头连接在一起。

在并联电路中，电阻器的总电阻等于各个电阻器电阻倒数之和的倒数。

设有n个并联的电阻器R1，R2，…，Rn，它们的电阻分别为R1，R2，…，Rn，则电阻器的总电阻R为：1/R = 1/R1 + 1/R2 + … + 1/Rn三、串并联电路的等效电阻计算有时候电路中既存在串联电路，又存在并联电路，此时需要根据具体情况进行计算。

1. 若电路先进行串联，再进行并联，计算步骤如下：- 首先，将串联电路的电阻器计算出总电阻R1；- 然后，将并联电路的电阻器计算出总电阻R2；- 最后，总电阻R等于R2。

2. 若电路先进行并联，再进行串联，计算步骤如下：- 首先，将并联电路的电阻器计算出总电阻R1；- 然后，将串联电路的电阻器计算出总电阻R2；- 最后，总电阻R等于R2。

请注意，以上的计算方法适用于只包含电阻器的简单电路。

在实际情况中，电路可能还包含电感、电容等元件，此时计算方法会更加复杂。

总结：了解如何计算串并联电路的等效电阻对于理解电路的性质和设计电路非常重要。

在串联电路中，电阻器的总电阻等于各个电阻器的电阻之和；在并联电路中，电阻器的总电阻等于各个电阻器电阻倒数之和的倒数。

根据具体情况，可以通过不同的计算步骤来计算串并联电路的等效电阻。

电路中的串并联与等效电阻电路的串联、并联是电路中最基础的连接方式，通过串并联可以实现电路中电阻、电流和电压的灵活组合。

在电路中，串联是指将多个电阻、电容或电感连接在一条路径上，而并联则是将多个电阻、电容或电感连接在一个节点上。

本文将详细介绍电路中的串并联以及等效电阻的原理与计算方法。

一、串联电路的特点与计算方法串联电路是指将多个电阻依次连接在一起，电流在各个电阻之间依次流动。

串联电路中，电流相同，电压分配根据电阻值的大小进行。

计算串联电路的总电阻时，只需将各个电阻值相加即可。

例如，有三个电阻分别为R1、R2和R3，它们依次串联在一起。

则串联电路的总电阻Rt可由以下公式计算得出：Rt = R1 + R2 + R3当电路中的电阻数量较多时，可以通过计算器或电路模拟软件来快速计算总电阻。

二、并联电路的特点与计算方法并联电路是指多个电阻、电容或电感连接在一个节点上，电压在各个元件之间相同，电流分配根据元件的电阻值进行。

在计算并联电路的总电阻时，需要应用并联电阻的公式。

例如，有三个电阻分别为R1、R2和R3，并联在一个节点上。

则并联电路的总电阻Rt可由以下公式计算得出：1/Rt = 1/R1 + 1/R2 + 1/R3类似地，当并联电路中的元件数量较多时，可以借助计算器或电路模拟软件来快速计算总电阻。

三、串并联电路的等效电阻在电路中，多个电阻、电容或电感可以通过串联或并联的方式组合在一起，形成串并联电路。

对于串并联电路，可以通过等效电阻来简化分析与计算。

对于串联电路，它的等效电阻等于各个电阻值的总和，如前述所示。

对于并联电路，它的等效电阻可以应用并联电阻公式进行计算。

当电路中既存在串联又存在并联时，可以借助串并联电路的等效电阻进行分析。

可将各个串并联电路的等效电阻依次计算，最终得到整个电路的等效电阻。

四、电路中的等效电阻应用等效电阻在电路设计与分析中有着重要的应用。

通过等效电阻，可以将复杂的电路简化为一个电阻，从而简化计算与分析的复杂度。

串并联电路中等效电阻计算公式在串并联电路中，我们需要确定电路中的等效电阻。

等效电阻是指将整个电路简化到一个等效电阻上，使得通过该等效电阻的电流与原始电路中的电流相同，通过该等效电阻的电压与原始电路中的电压相同。

对于串联电路，串联电阻等效值的计算公式为：R_eq = R1 + R2 + R3 + ... + Rn其中R_eq是等效电阻值，R1, R2, R3, ... Rn 是串联电路中各个电阻的阻值。

对于并联电路，并联电阻等效值的计算公式为：1/R_eq = 1/R1 +1/R2 + 1/R3 + ... + 1/Rn其中R_eq是等效电阻值，R1, R2, R3, ... Rn 是并联电路中各个电阻的阻值。

下面，我们将详细探讨串并联电路中等效电阻的计算公式。

1.串联电路中等效电阻：串联电路是指多个电阻依次连接在一起，形成一个单一路径的电路。

在串联电路中，电流在各个电阻中是相等的，而电压则是依次分配给每个电阻的。

因此，将整个电路简化到一个等效电阻上，使得通过该等效电阻的电流与原始电路中的电流相同，通过该等效电阻的电压与原始电路中的电压相同。

计算串联电路中的等效电阻的公式很简单，只需将各个电阻的阻值相加即可。

即：R_eq = R1 + R2 + R3 + ... + Rn例如，对于一个有三个电阻（R1=10Ω,R2=20Ω,R3=30Ω）的串联电路，其等效电阻为：R_eq = 10Ω + 20Ω + 30Ω = 60Ω2.并联电路中等效电阻：并联电路是指多个电阻并联在一起，形成多个并行路径的电路。

在并联电路中，电流会分流通过各个电阻，而电压则是各个电阻所在路径上的电压相等。

因此，将整个电路简化到一个等效电阻上，使得通过该等效电阻的电流与原始电路中的电流相同，通过该等效电阻的电压与原始电路中的电压相同。

计算并联电路中的等效电阻的公式需要注意，因为电阻是倒数关系，所以计算的时候需要将每个电阻的倒数相加，并将结果再次取倒数。