2020高一升高二预科班衔接教数学精品课程《第1讲集合及其运算》提升训练(附解析)
- 格式:pdf
- 大小:202.78 KB
- 文档页数:7

上海-高一数学同步讲义(2020新版)1.1集合的意义集合的运算-交集及其运算-B-1●十年一线教学经验沉淀●每年同步更新●优选全国题目,只为更好地贴合沪教版●四级大纲,按知识点按题型纵横编排●难度A-E五档覆盖不同层次学生●补差、培优、自招全体系覆盖●充分冗余,保证题型全面、保证题量充裕详尽答案、解析、word请联系作者1.1集合的意义-集合的运算-交集及其运算-B-11.设A={x|x≤1或x≥3},B={x|a≤x≤a+1},A∩B=B,则a的取值范围是.2.若集合A={x|x2﹣x﹣2=0},B={x|mx+1=0},若A∩B=B,则m=.3.定义集合M与N的新运算如下:M*N={x|x∈M∪N,且x∉M∩N}.若M={0,2,4,6,8,10,12},N={0,3,6,9,12,15},则(M*N)*M=.4.已知集合A={x||2x﹣1|<3},B={x|x2﹣(a+2)x+2a≤0}.(1)若a=1,求A∩B;(2)若A∩B=A,求实数a的取值范围.5.已知集合A={x|x2﹣3x+2=0},B={x|x2+2(a+1)x+(a2﹣5)=0},(Ⅰ)是否存在实数a,使B={﹣2}?(Ⅱ)若A∩B=B,求实数a的取值范围.6.已知集合A={x|a﹣1<x<2a+1},B={x|0<x<1}.(Ⅰ)若 ,求A∩B;(Ⅱ)若集合A不是空集,且A∩B=∅,求实数a的取值范围.7.已知集合A={x|2﹣a≤x≤2+a},B={x|x≤1或x≥4}.(1)当a=3时,求A∩B.(2)若A∩B=∅,求实数a的取值范围.8.已知集合A={a2,a+1,﹣3},B={a﹣3,2a+1,a2+3},若A∩B={﹣3},求实数a的值.(Wx:znufewangyang)9.已知A={x∈R|x2+2x+p=0}且A∩{x∈R|x>0}=∅,求实数p的取值范围.10.设集合A={(x,y)|y=x2+4x+6},B={(x,y)|y=2x+a},问:(1)a为何值时,集合A∩B有两个元素;(2)a为何值时,集合A∩B至多有一个元素.11.已知集合A={x|},B={x|p+1≤x<2p﹣1},A∩B=B,求实数p的取值范围.12.已知两个不同集合A={1,3,a2﹣a+3},B={1,5,a2+2a},A∩B={1,3},求a的值及集合A.(Wx:znufewangyang)13.已知集合A={x|x2﹣ax+a2﹣19=0},B={x|x2﹣5x+6=0},C={x|x2+2x﹣8=0}(1)当A=B时,求实数a的值;(2)当A∩C=∅,但A∩B≠∅时,求实数a的值.14.已知集合A={x|x2+2x+p=0},B={y|y=x2,x≠0},若A∩B=∅,求实数p的取值范围.15.已知集合A={x|x2+px﹣3=0},集合B={x|x2﹣qx﹣p=0|},且A∩B={﹣1},求2p+q的值.(Wx:znufewangyang)16.设集合P={x|﹣2≤x≤3},Q={x|2a≤x≤a+3}(1)若P∩Q=∅,求实数a的取值范围;(2)若P∩Q={x|0≤x≤3},求实数a的取值范围.。

⊂⊂⊂高一数学第一章集合与简易逻辑辅导讲义第一讲集合【辅导内容】 1、集合2、子集、全集、补集3、交集、并集 【学习内容】 一、集合的概念1、常用数集及其记法。
φ空集 N 非负整数集,自然数集 N +或N +正整数集 Z 整数集Q 有理数集 R 实数集 C 复数集 2、集合中元素的特征确定性;互异性;无序性, 会判断一组对象是否组成集合 3、集合的表示方法 ①列举法②描述法{x| p(x)} 4、集合的分类空集,有限集,无限集 二、子集,全集,补集1、掌握子集,真子集,全集,补集的概念及表示方法2、掌握子集,补集的性质①A ⊆B B ⊆C 则A ⊆C A ≠B B ≠C 则A ≠C②A ⊆BB ⊆A则A=B③Cu(CuA)=A ;CuU=φ,Cu φ=U ,CuA ⊆U ④φ⊆A ,A ⊆A三、交集、并集1、掌握交集、并集的概念及表示方法2、结合文氏图,掌握交集并集的性质①A ∩A=A ,A ∩φ=φA ∪A=A ,A ∪φ=A ②(A ∩B)⊆A ,(A ∩B)⊆B(A ∪B)⊇A ,(A ∪B)⊇B③A ∩B=B ∩A A ∪B=B ∪A ④若A ⊆B 则A ∩B=A 反之也其 若A ⊆B 则A ∪B=B 反之也其 ⑤(A ∩B) ⊆(A ∪B)当且仅当A=B 时,A ∩B= A ∪B⊂⊂3、结合文氏图及数轴会求两集合的交集,并集,补集四、1、理解奇数、偶数的定义,会用集合语言表示奇数集,偶数集、整数集之间的关系2、注意a 与{a}的区别,以及φ,0,{0}的区别。
【例题选讲】例1、已知集合A={x|ax 2+2x+1=0,a ∈R}(1)若A 只有一个元素,试求a 的值,并求出这个元素; (2)若A 是空集,求a 的取值范围;(3)若A 中至多有一个元素,求a 取值范围 分析:(1)集合只有一个元素时有两种情形: ①a=0,方程为2x+1=0,只有一个根为21-=x ②当a ≠0时,△=0,即4-4a=0,∴a=1,这时方程有两个相同的实数根x 1=x 2=-1 由①②可知,当a=0或a=1时,A 中只有一个元素,分别为21-或-1 (2)若A 为空集,则必须有⎩⎨⎧<-=∆≠0440a a ,解得a>1。

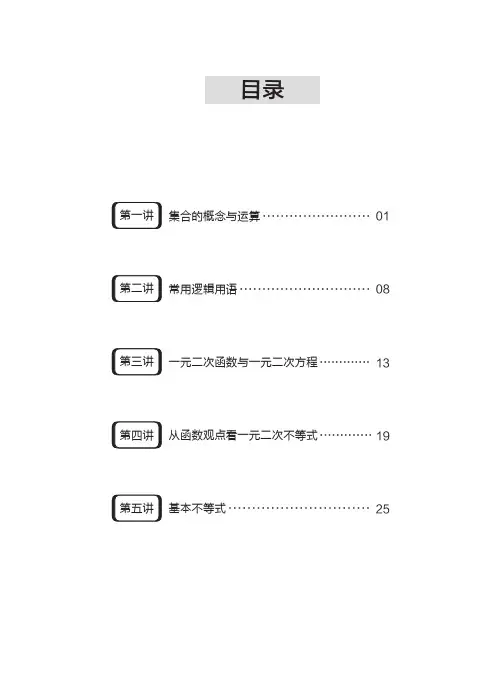


第03讲集合的基本运算,并能够运用这些语言解决集合运算知识点1并集1、并集的概念自然语言一般地,由所有属于集合A 或属于集合B 的元素组成的集合称为A 与B 的并集,记作A ∪B ,读作“A 并B ”符号语言A ∪B ={x |x ∈A 或x ∈B }图形语言2、并集的运算性质性质定义A B B A = 满足交换律A A A = 任何集合与其本身的并集等于这个集合本身A A A∅=∅= 任何集合与空集的并集等于这个集合本身()()A B C A B C = 多个集合的并集满足结合律()A A B ⊆ ,()B A B ⊆ 任何集合都是该集合与另一个集合并集的子集A B ⊆⇔A B B= 任何集合与它子集的并集都是它本身,反之亦然知识点2交集1、交集的概念自然语言由所有属于集合A 且属于集合B 的元素组成的集合,称为集合A 与B 的交集,记作A ∩B ,读作“A 交B ”符号语言A ∩B ={x |x ∈A 且x ∈B }图形语言2、交集的运算性质性质定义A B B A = 满足交换律A ∅=∅ 空集与任何集合的交集都是空集A A A= 集合与集合本身的交集仍为集合本身()()A B C A B C = 多个集合的交集满足结合律()()()A B C A C B C = 多个集合的综合运算满足分配律()()()A B C A C B C = 若A B A = ,则A B⊆交集关系与子集关系的转化()(),A B A A B B⊆⊆ 两个集合的交集是其中任一集合的子集知识点3全集与补集1、全集的概念自然语言一般地,如果一个集合包含所研究问题中涉及的所有元素,那么就称这个集合为全集,通常记为U .符号语言若,,,A U B U C U ⊆⊆⊆ ,则U 为全集.图形语言2、补集的概念自然语言若集合A 是全集U 的一个子集,由全集U 中不属于集合A 的所有元素组成的集合称为集合A 相对于全集U 的补集,记作U A ð.符号语言{}U A x x U x A =∈∉且ð图形语言3、补集的运算性质性质定义()U A A U= ð任何集合与其补集的并集为全集()U A A =∅ ð任何集合与其补集的交集为空集()UUA A=痧任何集合补集的补集为集合本身,U U U U=∅∅=痧全集的补集为空集,空集的补集为全集知识点4德摩根律与容斥原理1、德摩根定律:设集合U 为全集,A 、B 为U 的子集,则有(1)()()()U U U A B A B = 痧(2)()()()U U U A B A B = 痧2、容斥原理:在部分有限集中,我们经常遇到有关集合中元素的个数问题,常用Venn 图表示两集合的交、并、补。
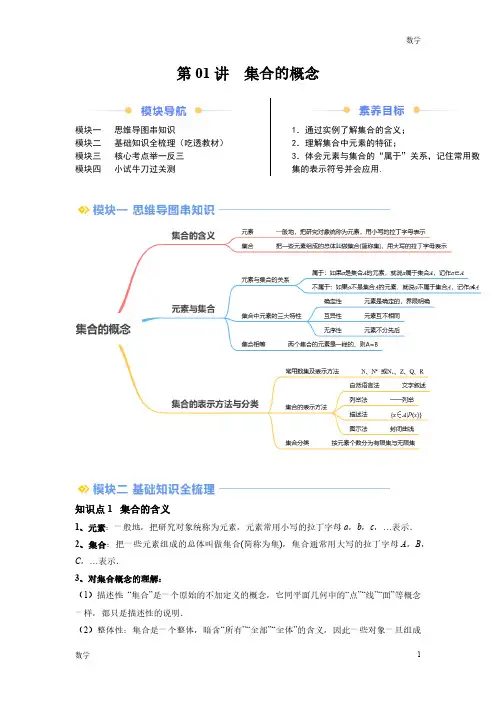
第01讲 集合的概念模块一 思维导图串知识模块二 基础知识全梳理(吃透教材)模块三 核心考点举一反三模块四 小试牛刀过关测1.通过实例了解集合的含义;2.理解集合中元素的特征;3.体会元素与集合的“属于”关系,记住常用数集的表示符号并会应用.知识点 1 集合的含义1、元素:一般地,把研究对象统称为元素,元素常用小写的拉丁字母a ,b ,c ,…表示.2、集合:把一些元素组成的总体叫做集合(简称为集),集合通常用大写的拉丁字母A ,B ,C ,…表示.3、对集合概念的理解:(1)描述性:“集合”是一个原始的不加定义的概念,它同平面几何中的“点”“线”“面”等概念一样,都只是描述性的说明.(2)整体性:集合是一个整体,暗含“所有”“全部”“全体”的含义,因此一些对象一旦组成了集合,这个集合就是这些对象的全体,而非个别对象.(3)广泛性:组成集合的对象可以是数、点、图形、多项式、方程,也可以是人或物等.知识点 2 元素与集合1、元素与集合的关系(1)属于:如果a 是集合A 的元素,就说a 属于集合A ,记作a ∈A ,读作a 属于A .(2)不属于:如果a 不是集合A 的元素,就说a 不属于集合A ,记作a ∉A ,读作a 不属于A .【注意】符号“∈”和“∉”只能用于元素与集合之间,表示元素与集合之间的从属关系,注意开口方向.2、集合中元素的三大特性(1)确定性:给定的集合,它的元素必须是确定的.也就是说,给定一个集合,那么任何一个元素在不在这个集合中就确定了.简记为“确定性”.【注意】如果元素的界限不明确,即不能构成集合.例如:著名的科学家、比较高的人、好人、很难的题目等.(2)互异性:一个给定集合中的元素是互不相同的.也就是说,集合中的元素是不重复出现的.简记为“互异性”.(3)无序性:给定集合中的元素是不分先后,没有顺序的.简记为“无序性”.3、集合相等:根据集合中元素的无序性,我们可以判断两个集合是否相等:只要构成两个集合的元素是一样的,我们就称两个集合是相等的。

集合的基本关系及运算【学习目标】1.理解集合之间包含与相等的含义,能识别一些给定集合的子集.在具体情境中,了解空集和全集的含义.2.理解两个集合的交集和并集的含义,会求两个简单集合的交集与并集.理解在给定集合中一个子集的补集的含义,会求给定子集的补集. 【要点梳理】要点一:集合之间的关系1.集合与集合之间的“包含”关系集合A 是集合B 的部分元素构成的集合,我们说集合B 包含集合A;子集:如果集合A 的任何一个元素都是集合B 的元素,我们说这两个集合有包含关系,称集合A 是集合B 的子集(subset).记作:A B(B A)⊆⊇或,当集合A 不包含于集合B 时,记作A B,用Venn 图表示两个集合间的“包含”关系:A B(B A)⊆⊇或要点诠释:(1)“A 是B 的子集”的含义是:A 的任何一个元素都是B 的元素,即由任意的x A ∈,能推出x B ∈. (2)当A 不是B 的子集时,我们记作“A ⊆B (或B ⊇A )”,读作:“A 不包含于B ”(或“B 不包含A ”). 真子集:若集合A B ⊆,存在元素x ∈B 且x A ∉,则称集合A 是集合B 的真子集(proper subset).记作:A B(或B A)规定:空集是任何集合的子集,是任何非空集合的真子集. 2.集合与集合之间的“相等”关系A B B A ⊆⊆且,则A 与B 中的元素是一样的,因此A =B要点诠释:任何一个集合是它本身的子集,记作A A ⊆.要点二:集合的运算 1.并集一般地,由所有属于集合A 或属于集合B 的元素所组成的集合,称为集合A 与B 的并集,记作:A ∪B 读作:“A 并B ”,即:A ∪B ={x|x ∈A,或x ∈B}Venn 图表示:要点诠释:(1)“x ∈A,或x ∈B ”包含三种情况:“,x A x B ∈∉但”;“,x B x A ∈∉但”;“,x A x B ∈∈且”. (2)两个集合求并集,结果还是一个集合,是由集合A 与B 的所有元素组成的集合(重复元素只出现一次).2.交集一般地,由属于集合A 且属于集合B 的元素所组成的集合,叫做集合A 与B 的交集;记作:A ∩B,读作:“A 交B ”,即A ∩B ={x|x ∈A,且x ∈B};交集的Venn 图表示:要点诠释:(1)并不是任何两个集合都有公共元素,当集合A 与B 没有公共元素时,不能说A 与B 没有交集,而是A B =∅.(2)概念中的“所有”两字的含义是,不仅“A ∩B 中的任意元素都是A 与B 的公共元素”,同时“A 与B 的公共元素都属于A ∩B ”.(3)两个集合求交集,结果还是一个集合,是由集合A 与B 的所有公共元素组成的集合. 3.补集 全集:一般地,如果一个集合含有我们所研究问题中所涉及的所有元素,那么就称这个集合为全集,通常记作U.补集:对于全集U 的一个子集A,由全集U 中所有不属于集合A 的所有元素组成的集合称为集合A 相对于全集U 的补集(complementary set),简称为集合A 的补集,记作:U U A A={x|x U x A}∈∉;即且;痧补集的Venn 图表示:要点诠释:(1)理解补集概念时,应注意补集U A ð是对给定的集合A 和()U A U ⊆相对而言的一个概念,一个确定的集合A ,对于不同的集合U,补集不同.(2)全集是相对于研究的问题而言的,如我们只在整数范围内研究问题,则Z 为全集;而当问题扩展到实数集时,则R 为全集,这时Z 就不是全集.(3)U A ð表示U 为全集时A 的补集,如果全集换成其他集合(如R )时,则记号中“U ”也必须换成相应的集合(即R A ð).4.集合基本运算的一些结论:A B A A B B A A=A A =A B=B A ⋂⊆⋂⊆⋂⋂∅∅⋂⋂,,,, A A B B A B A A=A A =A A B=B A ⊆⋃⊆⋃⋃⋃∅⋃⋃,,,,U U (A)A=U (A)A=⋃⋂∅,痧 若A ∩B =A,则A B ⊆,反之也成立 若A ∪B =B,则A B ⊆,反之也成立若x ∈(A ∩B),则x ∈A 且x ∈B 若x ∈(A ∪B),则x ∈A,或x ∈B求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn 图或数轴进而用集合语言表达,增强数形结合的思想方法. 【典型例题】类型一:集合间的关系例 1. 请判断①0{0} ;②{}R R ∈;③{}∅∈∅;④∅{}∅;⑤{}0∅=;⑥{}0∈∅;⑦{}0∅∈;⑧∅{}0,正确的有哪些?【答案】②③④⑧【试题解析】①错误,因为0是集合{}0中的元素,应是{}00∈;②③中都是元素与集合的关系,正确;④⑧正确,因为∅是任何集合的子集,是任何非空集合的真子集,而④中的{}∅为非空集合;⑤⑥⑦错误,∅是没有任何元素的集合.【总结升华】集合的符号语言十分简洁,因而被广泛用于现代数学之中,但往往容易混淆,其障碍在于这些符号与具体意义之间没有直接的联系,突破方法是熟练地掌握这些符号的具体含义.举一反三:【变式1】用适当的符号填空:(1) {x||x|≤1} {x|x 2≤1};(2){y|y =2x 2} {y|y =3x 2-1}; (3){x||x|>1} {x|x >1};(4){(x,y)|-2≤x ≤2} {(x,y)|-1<x ≤2}. 【答案】 (1)= (2) (3) (4)【总结升华】区分元素与集合间的关系,集合与集合间的关系.例2.(2015秋 确山县期中)已知A ={x |x 2―4=0},B ={x |ax ―6=0},且B 是A 的子集. (1)求a 的取值集合M ;(2)写出集合M 的所有非空真子集.【思路点拨】对(1)根据A 集合中的元素,B A ⊆,分类讨论B 的可能情况,再注解a ,写出集合M .根据含有n 个元素的集合的真子集个数是2n -1,求解(2).【答案】(1)M ={0,3,-3};(2){0},{3},{-3},{0,3},{0,-3},{3,-3} 【试题解析】(1)A ={2,-2}.∵B 是A 的子集,∴B =∅,{2},{-2}, ①B =∅时,方程ax -6=0无解,得a =0;②B ={2}时,方程ax -6=0的解为x =2,得2a -6=0,所以a =3;③B ={-2}时,方程ax -6=0的解为x =-2,得-2a -6=0,所以a =-3. 所以a 的取值集合M ={0,3,-3}.(2)M ={0,3,-3}的非空真子集为{0},{3},{-3},{0,3},{0,-3},{3,-3}【总结升华】本题考查集合的子集问题,含有n 个元素的集合的子集个数是2n ,真子集个数是2n -1;非空真子集个数是2n -2.举一反三:【变式1】已知{},a b A ⊆{},,,,a b c d e ,则这样的集合A 有 个.【答案】7个【变式2】同时满足:①{}1,2,3,4,5M ⊆;②a M ∈,则6a M -∈的非空集合M 有( ) A. 16个 B. 15个 C. 7个 D. 6个 【答案】C【试题解析】3a =时,63a -=;1a =时,65a -=;2a =时,64a -=;4a =时,62a -=;5a =时,61a -=;∴非空集合M 可能是:{}{}{}{}{}{}3,1,5,2,4,1,3,5,2,3,4,1,2,4,5,{}1,2,3,4,5共7个.故选C.【变式3】已知集合A ={1,3,a}, B ={a 2},并且B 是A 的真子集,求实数a 的取值.【答案】 a =-1, a =3±或a =0【试题解析】∵, ∴a 2∈A, 则有:(1)a 2=1⇒a =±1,当a =1时与元素的互异性不符,∴a =-1; (2)a 2=3⇒a =3±(3)a 2=a ⇒a =0, a =1,舍去a =1,则a =0综上:a =-1, a =3±或a =0.注意:根据集合元素的互异性,需分类讨论.【高清课堂:集合的概念、表示及关系377430 例2】例3. 设M ={x|x =a 2+1,a ∈N +},N ={x|x =b 2-4b +5,b ∈N +},则M 与N 满足( ) A. M =N B. M N C. N M D. M ∩N =∅【答案】B【试题解析】当a ∈N +时,元素x =a 2+1,表示正整数的平方加1对应的整数,而当b ∈N +时,元素x =b2-4b +5=(b -2)2+1,其中b -2可以是0,所以集合N 中元素是自然数的平方加1对应的整数,即M 中元素都在N 中,但N 中至少有一个元素x =1不在M 中,即M N,故选B.例 4.已知},,,0{},,,{y x N y x xy x M =-=若M =N ,则+++2()(x y x )()1001002y xy +++ = .A .-200B .200C .-100D .0【思路点拨】解答本题应从集合元素的三大特征入手,本题应侧重考虑集合中元素的互异性. 【答案】D【试题解析】由M =N,知M,N 所含元素相同.由0∈{0,|x|,y}可知0∈若x =0,则xy =0,即x 与xy 是相同元素,破坏了M 中元素互异性,所以x ≠0.若x ·y =0,则x =0或y =0,其中x =0以上讨论不成立,所以y =0,即N 中元素0,y 是相同元素,破坏了N 中元素的互异性,故xy ≠00,则x =y,M,N 可写为M ={x,x 2,0},N ={0,|x|,x}由M =N 可知必有x 2=|x|,即|x|2=|x| ∴|x|=0或|x|=1若|x|=0即x =0,以上讨论知不成立 若|x|=1即x =±1当x =1时,M 中元素|x|与x 相同,破坏了M 中元素互异性,故 x ≠1当x =-1时,M ={-1,1,0},N ={0,1,-1}符合题意,综上可知,x =y =-1∴+++2()(x y x )()1001002y x y +++ =-2+2-2+2+…+2=0【总结升华】解答本题易忽视集合的元素具有的“互异性”这一特征,而找不到题目的突破口.因此,集合元素的特征是分析解决某些集合问题的切入点.举一反三:【变式1】设a,b ∈R ,集合b {1,a+b,a}={0,,b}a,则b -a =( ) 【答案】2【试题解析】由元素的三要素及两集合相等的特征:b1{0,,b},0{1,a+b,a}a 0a b=0a∈∈≠∴+,又,∴当b =1时,a =-1,b{0,b}={0,-1,1}a∴,当b=1a时,∴b =a 且a +b =0,∴a =b =0(舍) ∴综上:a =-1,b =1,∴b -a =2. 类型二:集合的运算例5.(1)(2014 湖北武汉期中)已知{}22A y y x ==-;{}22B y y x ==-+,则A ∩B =( )A.()){}00,,, B.⎡⎣C.[-2,2]D.{(2)设集合M ={3,a },N ={x |x 2-2x <0,x ∈Z},M ∩N ={1},则M ∪N 为( ).A. {1,2,a }B. {1,2,3,a }C. {1,2,3}D. {1,3}【思路点拨】(1)先把集合A 、B 进行化简,再利用数轴进行相应的集合运算.(2)先把集合N 化简,然后再利用集合中元素的互异性解题.【答案】(1)C (2)D【试题解析】(1)集合A 、B 均表示构成相关函数的因变量取值范围,故可知:A ={y |y ≥-2},B ={y |y ≤2},所以A ∩B ={y |-2≤y ≤2},选C.(2)由N ={x |x 2-2x <0,x ∈Z}可得:N ={x |0<x <2,x ∈Z}={1},又由M ∩N ={1},可知1∈M ,即a =1,故选D. 举一反三:【变式1】设A 、B 分别是一元二次方程2x 2+px +q =0与6x 2+(2-p)x +5+q =0的解集,且A ∩B ={21},求A ∪B.【答案】{21, 31,-4} 【试题解析】∵A ∩B ={21}, ∴21是方程2x 2+px +q =0的解,则有: 0q p 21)21(22=++(1),同理有:6(21)2+(2-p)·21+5+q =0(2)联立方程(1)(2)得到:⎩⎨⎧-==.4q ,7p∴方程(1)为2x 2+7x -4=0,∴方程的解为:x 1=21, x 2=-4, ∴ }4,21{A -=,由方程(2) 6x 2-5x +1=0,解得:x 3=21, x 4=31,∴B ={21, 31},则A ∪B ={21, 31,-4}.【高清课堂:集合的运算377474 例5】【变式2】设集合A ={2,a 2-2a,6},B ={2,2a 2,3a -6},若A ∩B ={2,3},求A ∪B. 【答案】 {2,3,6,18}【试题解析】由A ∩B ={2,3},知元素2,3是A,B 两个集合中所有的公共元素,所以3∈{2,a 2-2a,6},则必有a 2-2a =3,解方程a 2-2a -3=0得a =3或a =-1当a =3时,A ={2,3,6},B ={2,18,3}∴A ∪B ={2,3,6}∪{2,18,3}={2,3,6,18} 当a =-1时,A ={2,3,6},B ={2,2,-9}这既不满足条件A ∩B ={2,3},也不满足B 中元素具有互异性,故a =-1不合题意,应舍去. 综上A ∪B ={2,3,6,18}.【高清课堂:集合的运算 377474 例6】例 6. 设全集U ={x ∈N +|x ≤8},若A ∩(C u B)={1,8},(C u A)∩B ={2,6},(C u A)∩(C u B)={4,7},求集合A,B.【答案】A ={1,3,5,8},B ={2,3,5,6} 【试题解析】全集U ={1,2,3,4,5,6,7,8}由A ∩(C u B)={1,8}知,在A 中且不在B 中的元素有1,8;由(C u A)∩B ={2,6},知不在A 中且在B 中的元素有2,6;由(C u A)∩(C u B)={4,7},知不在A 中且不在B 中的元素有4,7,则元素3,5必在A ∩B 中.由集合的图示可得A ={1,3,5,8},B ={2,3,5,6}. 类型三:集合运算综合应用例7.(2014 北京西城学探诊)已知集合A ={x |-4≤x <2}, B ={x |-1≤x <3},C ={x |x ≥a ,a ∈R}. (1)若(A ∪B )∩C =∅,求实数a 的取值范围;(2)若(A ∪B )ÜC ,求实数a 的取值范围.【思路点拨】(1)画数轴;(2)注意是否包含端点.【答案】(1)a ≥3 (2)a ≤-4 【试题解析】(1)∵A ={x |-4≤x <2}, B ={x |-1≤x <3},又(A ∪B )∩C =∅,如图,a ≥3;(2)画数轴同理可得:a ≤-4.【总结升华】此问题从表面上看是集合的运算,但其本质是一个定区间,和一个动区间的问题.思路是,使动区间沿定区间滑动,数形结合解决问题.举一反三:【变式1】已知集合P ={x ︱x 2≤1},M ={a }.若P ∪M =P,则a 的取值范围是( ) A.(-∞, -1] B.[1, +∞) C.[-1,1] D.(-∞,-1] ∪[1,+∞) 【答案】C【试题解析】P ={x ︱11x -≤≤}又 P M P =, ∴M P ⊆,∴ 11a -≤≤ 故选C.例8. 设集合{}{}222|40,|2(1)10,A x x x B x x a x a a R =+==+++-=∈.(1)若A B B =,求a 的值; (2)若A B B =,求a 的值.【思路点拨】明确A B 、A B 的含义,根据的需要,将其转化为等价的关系式B A ⊆和A B ⊆,是解决本题的关键.同时,在包含关系式B A ⊆中,不要漏掉B =∅的情况.【答案】(1)1a =或1a ≤-;(2)1a =. 【试题解析】 首先化简集合A ,得{}4,0A =-. (1)由AB B =,则有B A ⊆,可知集合B 为∅,或为{}0、{}4-,或为{}0,4-.①若B =∅时,224(1)4(1)0a a ∆=+--<,解得1a <-. ②若0B ∈,代入得21011a a a -=⇒==-或.当1a =时,{}{}2|400,4,B x x x A =+==-=符合题意;当1a =-时,{}{}2|00,B x x A ===⊆也符合题意.③若4B -∈,代入得2870a a -+=,解得7a =或1a =. 当1a =时,已讨论,符合题意;当7a =时,{}{}2|1648012,4B x x x =++==--,不符合题意.由①②③,得1a =或1a ≤-. (2),A B B A B =∴⊆.又{}4,0A =-,而B 至多只有两个根,因此应有A B =,由(1)知1a =.【总结升华】两个等价转化:,AB B A B A B B B A =⇔⊆=⇔⊆非常重要,注意应用.另外,在解决有条件A B ⊆的集合问题时,不要忽视A ≠∅的情况.举一反三:【变式1】(2015 源汇区一模)设A ={x |x 2+4x =0},B ={x |x 2+2(a +1)x +a 2-1=0},其中x ∈R ,如果A ∩B =B ,求实数a 的取值范围.【答案】a =1或a ≤-1【试题解析】A ={x |x 2+4x =0}={0,-4}, ∵A ∩B =B 知,B A ⊆,∴B ={0}或B ={-4}或B ={0,-4}或B =∅,若B ={0}时,x 2+2(a +1)x +a 2-1=0有两个相等的根0,则2002(1)001a a +=-+⎧⎨⨯=-⎩,∴a =-1,若B ={-4}时,x 2+2(a +1)x +a 2-1=0有两个相等的根-4,则24(4)2(1)4(4)1a a -+-=-+⎧⎨-⨯-=-⎩,∴a 无解, 若B ={0,-4}时,x 2+2(a +1)x +a 2-1=0有两个不相等的根0和-4,则2402(1)401a a -+=-+⎧⎨-⨯=-⎩,∴a =1, 当B =∅时,x 2+2(a +1)x +a 2-1=0无实数根,Δ=[2(a +1)]2-4(a 2-1)=8a +8<0,得a <-1,综上,a =1或a ≤-1.。

第一讲 集合及其运算一、选择题(每题5分,合计60分)8. 已知2{1,},{1,}M y y x x R P x x a a R ==-∈==-∈,则集合M 与P 的关系是( )A. M=PB. P R ∈ C . M ⊂≠P D. M ⊃≠P9. 设P 、Q 为两个非空实数集合,定义集合P+Q=},5,2,0{},,|{=∈∈+P Q b P a b a 若}6,2,1{=Q ,则P+Q 中元素的个数是( )A .9B .8C .7D .6 10. 设全集{(,),},I x y x y R =∈集合3{(,)1},{(,)1}2y M x y N x y y x x -===≠+-,那么()()I I C M C N ⋂等于 ( )A. ∅B.{(2,3)}C. (2,3)D.{(,)1}x y y x ≠+11. 设U 为全集,集合A 、B 、C 满足条件A B A C ⋃=⋃,那么下列各式中一定成立的是( ) A.A B A C ⋂=⋂ B.B C =C. ()()U U A C B A C C ⋂=⋂D. ()()U U C A B C A C ⋂=⋂12.2{60},{10}A x x x B x mx =+-==+=,且A B A ⋃=,则m 的取值范围是( )A.11{,}32-B. 11{0,,}32--C. 11{0,,}32-D. 11{,}32二、填空题(共4题,每题4分,计16分)13/ 若集合{}|6,A x x x N =≤∈,{|}B x x =是非质数,C A B =,则C 的非空子集的个数为 /14/ 若集合{}|37A x x =≤<{}|210B x x =<<,则A B =_____________/15.设集合{32}A x x =-≤≤,{2121}B x k x k =-≤≤+,且A B ⊇,则实数k 的取值范围是 /16/已知知{}{}221,21A y y x x B y y x ==-+-==+,则A B =_________/三、解答题(共6题,合计74分)17/ (原创)(本题满分12分)某班有学生55人,其中体育爱好者43人,音乐爱好者34人,还有4人既不爱好体育也不爱好音乐,求该班既爱好体育又爱好音乐的人数/18. (本题满分12分)已知集合A=()(){}222110y y a a y a a -++++> , B=215,0322y y x x x ⎧⎫=-+≤≤⎨⎬⎩⎭,A∩B=φ,求实数a 的取值范围.19/ 已知A={x ︱x 2-3x+2=0},B={x ︱ax -2=0},且满足B A ⊆,求实数a的取值范所组成的集合C /20/(本题满分12分)已知集合{}{}22,1,3,3,21,1A a a B a a a =+-=--+,若A∩B={-3},求实数a 的值21.(本题满分12分)设}01)1(2|{},04|{222=-+++==+=a x a x x B x x x A ,若B B A =⋂,求a 的值22.(本题满分14分)已知集合A={|}x y =使,集合B={|}y y =使 ,A=B 是否可能成立?如可能成立,求出使A=B 的a 的取值范围,如不可能成立,说明理由.第一章 集合全章检测参考解析 一、选择题:1/ 答案: C 解析:主要考察元素的确定性; 2/ 答案: D解析: 选项A 所代表的集合是{}0并非空集,选项B 所代表的集合是{}(0,0)并非空集,选项C 所代表的集合是{}0并非空集,选项D 中的方程210x x -+=无实数根;3/ 答案: D 解析: 当0m =时,,B φ=满足AB A =,即0m =;当0m ≠时,1,B m ⎧⎫=⎨⎬⎩⎭而A B A =,∴11111m m=-=-或,或;∴1,10m =-或; 4/ 答案: A解析: 阴影部分完全覆盖了C 部分,这样就要求交集运算的两边都含有C 部分; 5/ 答案: D 解析:由元素的互异性a b c ≠≠可得答案; 6/ 答案: C解析:由{}0,1,3A =,其真子集有3217-=/7. 答案: A解析: (1)最小的数应该是0,(2)反例:0.5N -∉,但0.5N ∉(3)当0,1,1a b a b ==+=,(4)元素的互异性8.答案: A 解析:由x 2≥0,而︱a ︱≥0,则M=P . 9. 答案:B解析:分别取P 、Q 为两个非空实数集中的元素相加,可知所得的结果有8个。

第一章第三节集合的基本运算一、电子版教材二、教材解读知识点集合的运算1.由所有属于集合A或属于集合B的元素组成的集合叫A与B的并集,记作A∪B;符号表示为A∪B={x|x ∈A或x∈B}2.并集的性质A∪B=B∪A,A∪A=A,A∪∅=A,A⊆A∪B.3.对于两个给定的集合A、B,由所有属于集合A且属于集合B的元素组成的集合叫A与B的交集,记作A∩B。
符号为A∩B={x|x∈A且x∈B}。
4.交集的性质A∩B=B∩A,A∩A=A,A∩∅=∅,A∩B⊆A.5、对于一个集合A,由全集U中不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集,记作∁U A。
符号语言:∁U A={x|x∈U,且x∉A}。
【例题1】(2020·全国高一)已知集合,,,则的子集共有()A.2个B.3个C.8个D.4个【答案】D【解析】,的子集有,,,,共个.【例题2】(2020·山东省邹城市第一中学高三其他)已知集合,,则()A.B.C.D.【答案】D【解析】,,,故选:D.【例题3】(2020·安徽省舒城中学高二月考(文))已知集合,则=A.B.C.D.【答案】C【解析】由题意得,,则.故选C.【例题4】(2020·肥城市教学研究中心高三其他)已知全集,集合,,则()A.B.C.D.【答案】B【解析】由题可知,则.【例题5】(2020·重庆高三月考(文))已知全集为R,集合,,则()A.B.C.D.【答案】C【解析】,则.故选:C.【例题6】(2020·全国高一)设全集为,,.(1)求;(2)求.【解析】(1)由题意;(2)由题意,∴或.【例题7】(2020·全国高一)已知集合,,.(1)若,求;.(2)若,求实数的取值范围.【解析】(1)若时,,∴,由或,所以(2)由知当时∴当时或∴或综上:的取值范围是.三、素养聚焦1.已知集合,则=()A.B.C.D.【答案】D【解析】,所以.故选:D2.已知集合,,则A.B.C.D.【答案】C【解析】集合,而,所以,故选C.3.已知集合,则()A.B.C.D.【答案】C【解析】因为集合,,故.故选:C4.若集合,,则()A.B.C.D.【答案】A【解析】由于集合,,所以5.已知集合A={x|﹣1<x<5},B={1,3,5},则A∩B=()A.{1,3}B.{1,3,5}C.{1,2,3,4}D.{0,1,2,3,4,5}【答案】A【解析】∵A={x|﹣1<x<5},B={1,3,5},∴A∩B={1,3}.故选:A.6.若集合,,则()A.B.C.D.【答案】A【解析】因为,,所以.7.已知集合,,则().A.B.C.D.【答案】D【解析】,所以.8.满足条件的所有集合A的个数是()A.1B.2C.3D.4【答案】D【解析】因为,所以,集合A可能为,即所有集合A的个数是4,故选D.9.已知集合,满足,则下列关系式恒成立的是()A.P⫋S B.C.D.S⫋P 【答案】B【解析】集合,满足,中的元素都在集合中,.10.已知集合I,M,N的关系如图,则I,M,N的关系为().A.B.C.D.【答案】C【解析】由韦恩图可知,N M I,11.设,,则必有().A.B.A B C.D.【答案】D【解析】,,12.设全集,集合,,那么是().A.B.C.D.【答案】A【解析】因为全集,集合,,所以,,所以,13.已知集合,集合,().A.B.C.D.【答案】B【解析】,,故14.已知全集,集合,,则()A.B.C.D.【答案】A【解析】,则15.已知集合或,集合,则()A.B.C.D.【答案】A【解析】依题意,所以.16.已知函数的定义域为A,则()A.或B.或C.D.【答案】D【解析】已知函数的定义域为,所以,得,即,故.17.设集合,则()A.B.C.D.【答案】C【解析】首先注意到集合A与集合B均为点集,联立,解得,或,从而集合,18.下列表示图形中的阴影部分的是()A.B.C.D.【答案】A【解析】由已知中阴影部分所表示的集合元素满足“是的元素且是的元素,或是的元素”,故阴影部分所表示的集合是19.集合A,B,C满足,则成立的等式是().A.B.C.D.【答案】B【解析】因为,所以且,而集合不一定相等,所以选项A,C,D错误;又由可知,故B做正确.20.如图所示的韦恩图中,A、B是非空集合,定义表示阴影部分的集合,若x,y∈R,,则A*B为()A.B.或C.或D.或【答案】B【解析】依据定义,就是指将除去后剩余的元素所构成的集合;对于集合A,求的是函数的定义域,解得:;对于集合B,求的是函数的值域,解得;依据定义,借助数轴得:或.21.设全集为定义集合与的运算:且,则()A.B.C.D.【答案】B【解析】且22.设集合,,若,则的取值范围为()A.B.C.D.【答案】D【解析】因为,所以,解得或.23.设集合,则=()A.B.C.D.【答案】A【解析】∵,∴,∴24.已知集合,,则=()A.B.C.D.【答案】B【解析】由可得:解得,即,则25.设集合,,则()A.B.C.D.【答案】D【解析】由题意,集合,集合,所以,所以.故选:D.26.已知非空集合A,B满足以下两个条件2,3,4,5,,;若,则.则有序集合对的个数为A.12B.13C.14D.15【答案】A【解析】由题意分类讨论可得:若,则3,4,5,;若,则3,4,5,;若,则2,4,5,;若,则2,3,5,;若,则3,4,1,;若,则4,5,;若,则3,5,;若,则3,4,;若,则3,5,;若,则3,4,;若,则2,4,;若3,,则4,.综上可得:有序集合对的个数为12.27.已知集合,,则()A.B.C.D.【答案】A【解析】由已知得,因为,所以,故选A.28.某单位周一、周二、周三开车上班的职工人数分别是14,10,8.若这三天中至少有一天开车上班的职工人数是20,则这三天都开车上班的职工人数至多是()A.5B.6C.7D.8【答案】B【解析】如图所示,(a+b+c+x)表示周一开车上班的人数,(b+d+e+x)表示周二开车上班人数,(c+e+f+x)表示周三开车上班人数,x表示三天都开车上班的人数,则有:,即,即,当b=c=e=0时,x的最大值为6,即三天都开车上班的职工人数至多是6.29.设集合,都是的含两个元素的子集,且满足:对任意的,(),都有(表示两个数,中的较大者),则的最大值是()A.B.C.D.【答案】B【解析】根据题意,对于M,含2个元素的子集有15个,但{1,2}、{2,4}、{3,6}只能取一个;{1,3}、{2,6}只能取一个;{2,3}、{4,6}只能取一个,故满足条件的两个元素的集合有11个;30.当一个非空数集满足“如果,则,且时,”时,我们称就是一个数域,以下四个关于数域的命题:①是任何数域的元素;②若数域有非零元素,则;③集合是一个数域;④有理数集是一个数域,其中真命题有()A.个B.个C.个D.个【答案】C【解析】①:当时,有,所以是任何数域的元素,正确;②:取为实数域,令,,则,正确;③:若为数域,取,,则不成立,错误;④:取有理数,,令,,则有理数集,有理数集,有理数集,且有理数集(),所以有理数集是数域.正确的有:①②④.31.全集,非空集合,且中的点在平面直角坐标系内形成的图形关于轴、轴和直线均对称.下列命题:①若,则;②若,则中至少有8个元素;③若,则中元素的个数一定为偶数;④若,则.其中正确命题的个数是()A.1B.2C.3D.4【答案】C【解析】中的点在平面直角坐标系内形成的图形关于轴、轴和直线均对称.所以当,则有,,,进而有:,,,①若,则,正确;②若,则,,,能确定4个元素,不正确;③根据题意可知,,若能确定4个元素,当也能确定四个,当也能确定8个所以,则中元素的个数一定为偶数正确;④若,由中的点在平面直角坐标系内形成的图形关于轴、轴和直线均对称可知,,,,即,故正确,综上:①③④正确.故选C.32.已知集合,若,则实数的取值范围为()A.B.C.D.【答案】C【解析】试题分析:集合,若,则,所以有,所以,故选C.33.(多选题)给定数集,若对于任意,,有,且,则称集合为闭集合,则下列说法中不正确的是()A.集合为闭集合B.正整数集是闭集合C.集合为闭集合D.若集合,为闭集合,则为闭集合【答案】ABD【解析】A.当集合时,,而,所以集合不为闭集合.B.设是任意的两个正整数,当时,不是正整数,所以正整数集不为闭集合.C.当时,设则(?为∈),,所以集合是闭集合.D.设,由C可知,集合,为闭集合,,而,此时不为闭集合.所以说法中不正确的是ABD34.(多选题)集合,是实数集的子集,定义,叫做集合的对称差,若集合,,则以下说法正确的是()A.B.C.D.E.【答案】BCD【解析】,,故,..35.(多选题)已知集合,,则()A.集合B.集合可能是C.集合可能是D.0可能属于B【答案】ABD【解析】∵,∴,故A正确.∵集合,∴集合中一定包含元素1,2,3,∵,∴集合可能是,故B正确;∵不是自然数,∴集合不可能是,故C错误;∵0是最小的自然数,∴0可能属于集合,故D正确.。
第一节集合的含义与关系知识点: (1)集合:某些指定的集在一起就成为一个集合.常用大写字母A、B、C等来表示.(2)常用的数集及记法:①非负整数集(自然数集)全体非负整数的集合.记作.②正整数集:非负整数集内排除0的集合.记作③整数集:全体整数的集合.记作④有理数集:全体有理数的集合.记作⑤实数集:全体实数的集合.记作(3)元素及元素与集合的关系:元素:集合中的每个叫做这个集合的元素.常用小写字母a,b,c,……来表示.如果a是集合A中的元素,就说a属于A,记作a A,否则a A.(4)列举法:把集合中的元素一一列举出来,写在大括号“{}”内,元素与元素之间用“,”分开,这样的表示方法叫列举法.(5)描述法:用确定的条件表示某些对象是否属于这个集合的方法叫描述法.(6)有限集:含有有限个元素的集合叫有限集.(7)无限集:含有无限个元素的集合叫无限集.(8)集合中的元素必须具有三大特性“”.①:是指集合中的元素必须是确定的,即任何一个对象都能判断它是或不是某个集合的元素,二者必居其一.如“接近于0的实数”接近由于没有一个确定的界性,故0.001是否属于这个集合不能判断,所以这不能组成一个集合.②:是指集合中的元素互不相同,即同一个集合中不能出现同一个元素两次,如:{1,0,a2}表示一个集合,则 a≠±1.③:集合中的元素无先后顺序,如{1,2}与{2,1}是同一个集合.二、集合间的基本关系1 子集:对于集合A与B,如果集合A的任何一个元素都是集合B的元素,我们就说集合A包含于集合B,或集合B包含集合A,记作:A B(或B A),图1—1所示表示:这时我们也说集合A是集合B的子集.2 集合的相等:对于两个集合A与B,如果集合A的任何一个元素都是集合B的元素,同时集合B的任何一个元素都是集合A的元素.我们说集合A等于集合B,记作:A=B.即对于集合A,B,如果A B,同时B A,那么A=B.B,并且A≠B,我们就说集合A是集合B的真子集,记作A 3.真子集:对于两个集合A与B,如果AB(或B A).4.空集是5 知识拓宽含有n 个元素的集合有几个子集?问:∈与⊆的区别是什么?[例1]若A ={a ,b };B ={x |x ∈A },则集合A 与集合B 的关系是( )A .B ⊆A B .B AC .B ∈AD .B ∉A[例2]已知A ={x|x <-1或x >2},B ={x|4x +p <0},当A ⊇B 时,求实数p 的取值范围.答案:p ≥4[例3]下列集合中表示空集的是( )A .{x ∈R|x +5=5}B .{x ∈R|x +5>5}C .{x ∈R|x 2=0}D .{x ∈R|x 2+x +1=0}一、选择题1.在“①很大的有理数;②方程x 2+1=0的实数根;③直角坐标平面的第二象限的一些点;④所有等腰直角三角形”中,能够表示成集合的是A .②B .②③④C .②④D .①②③④答案C 提示:因为“大”“一些”没有具体的界线.2.方程组⎩⎨⎧=-=+13y x y x 的解集是 A .{2,1} B .{x =2,y =1} C .{(2,1)} D .{(x ,y)|(2,1)}答案D 提示:因为⎩⎨⎧=-=+1y x 3y x 的解为⎩⎨⎧==1y 2x 写成集合的形式为{(x ,y)|(2,1)}.3.下列四个关系式中,正确的是A .集合N 中最小元素为1B .0.7∈QC .{a }∈{a ,b }D .{a }∈a答案B4.下列各题中的M 与P 表示同一个集合的是A .M ={(1,-3)} P ={(-3,1)}B .M ={3,4} P ={(3,4)}C .M ={y |y =x 2+1,x ∈R } P ={(x ,y)|y =x 2+1,x ∈R }D .M ={y |y =x 2+1,x ∈R } P ={t |t =(y -1)2+1,y ∈R }答案D 提示:因为(1,-3)与(-3,1)是不同的点,而C 中M 是数集,P 是点集.二、填空题5.设21∈{x |x 2-ax -25=0},则a =_________.答案-29 提示:由题意知21是x 2-ax -25=0的一个根,所以,252141--a =0,所以a =-296.设A ={x |x =2k ,k ∈Z },B ={x |x =2k -1,k ∈Z },C ={x |x =4k +1,k ∈Z },a ∈A ,b ∈B ,则a +b ∈_________.填(A 或B 或C)答案B 提示:因为A 是偶数集,B 是奇数集.∴a +b 是奇数.即a +b ∈B .7.{n |5n是整数,|n |≤20}=_________.答案 提示:{n |5n是整数,|n |≤20}={-20,-15,-10,-5,0,5,10,15,20}三、解答题8.若-3∈{a 2-2a -3,2a 2-a -4,a 2+1},求实数a 的值构成的集合.答案解:∵-3∈{a 2-2a -3,2a 2-a -4,a 2+1}.∴a 2-2a -3=-3或2a 2-a -4=-3.∴a =0,2,1,-21.经检验a =0,2,1,-21均合题意.∴a 的值构成的集合为{0,2,1,-21}.【同步达纲练习】一、选择题1.下列关系不正确的是A .R ⊆QB .R ⊇ZC .N ⊆ND .Z ⊆Q2.设集合A ={x |x ≤10},a =3,则A .a AB .a ∉AC .{a }∈AD .{a }A3.设M ={x |x >}31,则①0⊆M ,②∅⊆M ,③{0}M ,④{31}M ,其中正确命题的个数是A.1 B.2 C.3 D.44.集合M={y|y=x2-2x-1,x∈R},N={x|-2≤x≤4,x∈R},则M与N的关系是A.M=N B.M N C.M N D.无法确定5.下面四个命题正确的是:A.任何一个集合必有两个或两个以上的子集 B 空集是任何集合的子集C.空集有真子集 D.∅={0}二、填空题6.集合M={0},N={x|x2+1=0,x∈R},则M_________N.⊆{0,1,2,3,4}的不同集合M有___________.7.满足{1,0}M⊆{1,2,3,4,5};②对于M中的任何一个元素a,都能使得6-a∈M.则8.非空集合M满足①M同时满足①,②的M共有_________个.三、解答题9.设A={x|x≥-2-b,b∈R},B={y|y=2x2+1,x∈R}.当A B时,求b的取值集合.10 设集合A={x| x2+4x=0},B ={x| x2+2(a+1)x+ 2a-1=0 , a∈R} 若B⊆A ,求实数a 的取值范围。
高一数学预科班讲义(总25页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--高一数学预科第1讲:集合及其运算一、集合的含义与表示:1.集合的表示方法:① ② ③2.关于集合的元素的特征:(1)确定性:设A 是一个给定的集合,x 是某一个具体对象,则或者是A 的元素,或者不是A 的元素,两种情况必有一种且只有一种成立。
(2)互异性:一个给定集合中的元素,指属于这个集合的互不相同的个体(对象),因此,同一集合中不应重复出现同一元素。
(3)无序性:一般不考虑元素之间的顺序,但在表示数列之类的特殊集合时,通常按照习惯的由小到大的数轴顺序书写。
3.集合元素与集合的关系用“属于”和“不属于”表示; (1)如果a 是集合A 的元素,就说a 属于A ,记作a ∈A(2)如果a 不是集合A 的元素,就说a 不属于A ,记作a ∉A (“∈”的开口方向,不能把a ∈A 颠倒过来写)4.常用数集的记法:(1)非负整数集(自然数集):全体非负整数的集合记作N ,{} ,2,1,0=N(2)正整数集:非负整数集内排除0的集记作N *或N + {} ,3,2,1*=N (3)整数集:全体整数的集合记作Z , {} ,,,210±±=Z(4)有理数集:全体有理数的集合记作Q , {}整数与分数=Q(5)实数集:全体实数的集合记作R {}数数轴上所有点所对应的=R5.两个集合相等:如果两个集合所含的元素完全相同,则称这两个集合相等。
6. 有限集合、无限集合、空集的定义 例题1.下列各组对象不能组成集合的是( )A.大于6的所有整数B.高中数学的所有难题C.被3除余2的所有整数D.函数y=x1图象上所有的点 练习:下列条件能形成集合的是( )A.充分小的负数全体B.爱好足球的人C.中国的富翁D.某公司的全体员工例题2、填空:或用符号∉∈(1) -3 N ; (2) Q ; (3)31Q ; (4)0 Φ ;(5)3 Q ; (6)21- R ; (7)1 N +; (8)π R 。
1.3集合的基本运算第2课时全集与补集课后训练·巩固提升UB.{0,2}C.{-1,2}D.{-1,0,2}U={-1,0,1,2},P={x∈Z|-√2<x<√2}={-1,0,1},所以∁U P={2},故选A.()A.A∩(∁U B)B.(∁U A)∩B∩B) D.∁U(A∪B)Venn图可以看出,阴影部分是A中去掉B那部分所得,即阴影部分的元素属于A,且不属于B,∁U B).U={x∈R|-2≤x≤2},A={x∈R|-2≤x≤0},则∁U A等于()A.{x|0<x<2}B.{x|0≤x<2}<x≤2} D.{x|0≤x≤2}U={x∈R|-2≤x≤2},A={x∈R|-2≤x≤0},∴∁U A={x|0<x≤2},故选C.U=Z,A={0,1,2,3},B={x|x2=2x},则A∩(∁U B)等于()A.{1,3}B.{0,2}D.{2}U=Z,A={0,1,2,3},B={x|x2=2x}={0,2},所以∁U B={x|x∈Z,且x≠0,且x≠2},所以B)={1,3}.I={1,2,3,4,5,6,7,8},集合M={3,4,5},N={1,3,6},则集合{2,7,8}是()A.M∪NB.M∩N)∪(∁I N) D.(∁I M)∩(∁I N)全集I={1,2,3,4,5,6,7,8},集合M={3,4,5},集合N={1,3,6},N={1,3,4,5,6},M∩N={3},∁I M={1,2,6,7,8},∁I N={2,4,5,7,8},)∪(∁I N)={1,2,4,5,6,7,8},(∁I M)∩(∁I N)={2,7,8},故选D.U=R,集合A={x|x<-2,或x>4},B={x|-3≤x≤3},则(∁U A)∩B等于()A.{x|-3≤x≤4}B.{x|-2≤x≤3}C.{x|-3≤x≤-2,或3≤x≤4}≤x≤4}U=R,A={x|x<-2,或x>4},可得∁U A={x|-2≤x≤4}.∁U A和B,如图.(∁U A)∩B={x|-2≤x≤3}.U=R,A={x|x<-1,或x≥3},B={x|x>2},求:(1)∁U A;∪(∁U B).因为全集U=R,A={x|x<-1,或x≥3},所以∁U A={x|-1≤x<3}.B={x|x>2},所以∁U B={x|x≤2}.所以A∪(∁U B)={x|x≤2,或x≥3}.U={2,3,a2-2a-3},A={2,|a-7|},∁U A={5},求实数a的值.∁U A={5},可知5∈U,且5∉A,所以a2-2a-3=5,且|a-7|≠5,解得a=-2或a=4.事实上,当a=-2时,|a-7|=9,A={2,9},U={2,3,5},则A 不是U 的子集,不合题意;Z B.P C.Q D.⌀M={x|x=3k ,k ∈Z },表示被3整除的整数组成的集合,P={x|x=3k+1,k ∈Z },表示被3除余数,Q={x|x=3k-1,k ∈Z }={x|x=3n+2,n ∈Z },表示被3除余数为2的整数组成的集∪Q 表示被3除余数为1或余数为2的整数组成的集合,故∁Z (P ∪Q )=M.U={x ∈N +|x<9},(∁U A )∩B={1,6},A ∩(∁U B )={2,3},∁U (A ∪B )={5,7,8},则集合B=( )A.{2,3,4}B.{1,4,6}D.{1,2,3,6},可得U={1,2,3,4,5,6,7,8},根据题意作出Venn 图,如图.B={1,4,6}.{0,1,2,3},A={x ∈U|x 2+mx=0},若∁U A={1,2},则实数m= .U={0,1,2,3},∁U A={1,2},=-m ,即m=-3.3A={x|x ≤a },B={x|1≤x ≤2},且A ∪(∁R B )=R ,则实数a 的取值范围是 .B={x|1≤x ≤2},R {x|x<1,或x>2},又A ∪(∁R B )=R ,≤x ≤2}⊆A ,∴a ≥2.≥2U 为全集,集合A={1,3,x },B={1,x 2},若B ∪(∁U B )=A ,则∁U B= .B ∪(∁U B )=A ,∴U=A.A ,∴x 2=3,或x 2=x ,解得x=±√3或x=0或x=1.当x=√3时,B={1,3},A={1,3,√3},∴∁U B={√3};当x=-√3时,B={1,3},A={1,3,-√3},∴∁U B={-√3};当x=0时,B={1,0},A={1,3,0},∴∁U B={3};当x=1时,B={1,1},不符合集合元素的互异性,舍去.,∁U B={√3}或{-√3}或{3}.√3}或{-√3}或{3}A={x|-1≤x ≤3},B={x|m-2≤x ≤m+2,x ∈R }.(1)若A ∩B={x|0≤x ≤3},求实数m 的值;A ∩(∁RB )=A ,求实数m 的取值范围.因为A ∩B={x|0≤x ≤3},所以{m -2=0,m +2≥3,解得m=2. (2)因为B={x|m-2≤x ≤m+2,x ∈R },所以∁R B={x|x<m-2,或x>m+2},又由A ∩(∁R B )=A ,可得A ⊆∁R B ,所以有m-2>3,或m+2<-1,解得m>5,或m<-3.。