六年级数学下册知识重点结构图
- 格式:docx
- 大小:1.05 MB
- 文档页数:30

期中复习讲义(苏教版)2020-2021学年苏教版数学六年级下册期中章节复习精编讲义第一单元《扇形统计图》知识互联网知识导航一、扇形统计图的意义:用整个圆的面积表示总数,用圆内各个扇形面积表示各部分数量同总数之间的关系。
也就是各部分数量占总数的百分比(因此也叫百分比图)。
二、常用统计图的优点:1、条形统计图:可以清楚的看出各种数量的多少。
2、折线统计图:不仅可以看出各种数量的多少,还可以清晰看出数量的增减变化情况。
3、扇形统计图:能够清楚的反映出各部分数量同总数之间的关系。
三、扇形面积的大小表示的意义:在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关,圆心角越大,扇形越大。
(因此扇形面积占圆面积的百分比,同时也是该扇形圆心角度数占圆周角度数的百分比。
)夯实基础一、精挑细选(共5题;每题2分,共10分)1. (2020六上·甘井子期末)要统计分析淘气和笑笑一到六年级每年身高变化情况,应选择()。
A. 条形统计图B. 折线统计图C. 扇形统计图D. 复式折线统计图2. (2020六上·宝安期末)在学过的统计图中,要想直观表示出各部分数量同总数量之间的关系,用()统计图比较合适。
A. 圆形统计图B. 条形统计图C. 折线统计图D. 扇形统计图3. (2020六上·龙华期末)六年级书屋各类书籍情况统计如图所示,其中文学类有240本。
下面说法错误的是()。
A. 六年级书屋共有800本书B. 科技类的书最多C. 漫画类的书占总数的20%D. 其他类的书有144本4. 某班13位同学参加每周一次的卫生大扫除,按学校的卫生要求需要完成总面积为80㎡的三个项目的任务,三个项目的面积比例和每人每分钟完成各项目的工作量如图所示:从统计图中可知:4人擦完全部玻璃的时间是()分钟.A. 1B. 3C. 4D. 55. 如图是甲﹑乙两户居民家庭全年各项支出的统计图.根据统计图,下列对两户家庭教育支出占全年总支出的百分比作出的判断中正确的是()A. 甲户比乙户大B. 乙户比甲户大C. 甲﹑乙两户一样大D. 无法确定哪一户大二、判断正误(共5题;每题1分,共5分)6.(2021六上·新会月考)扇形统计图能清楚地看出数量的多少和数量变化的情况。

人教版新课标六年级数学下册(4~6单元)重点知识归纳四会市龙湾学校:练志强2012年1月第四单元:统计1.扇形统计图及其特点:扇形统计图是用整个圆表示总数,用圆内各个扇形的大小表示各部分数量占总数的百分数;从扇形统计图中可以清楚地看出各部分数量同总数之间的关系。
2.制作统计图时,一定要客观准确地反映信息;在分析统计图时,不要被模糊数据所误导,一定要认真分析,准确提取统计信息。
3.折线统计图及其特点:折线统计图是用一个单位长度表示一定的数量,根据数量的多少描出各点,然后把各点用线段顺次连接起来。
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况。
4.在根据统计图进行比较、判断时要注意统一标准。
5.温馨提示:当扇形统计图中“其他”部分的占有率比已知占有率最小的部分大时,不能判定已知占有率最小的部分所代表的数据最小。
第五单元:数学广角1.“抽屉原理”(一):把m个物体任意放进n个空抽屉里(m>n,n是0非自然数),那么一定有一个抽屉中放进了至少2介物体。
2.“抽屉原理”(二):把多于kn个的物体任意分放进n个空抽屉(k是正整数),那么一定有一个抽屉中放进了至少(k+1)个物体。
3.用“抽屉原理”解题的一般步骤是:(1)分析题意,把实际问题转化为“抽屉原理”,即弄清“抽屉”(“抽屉”是什么,有几个抽屉)和分放物体。
(2)设计“抽屉”的具体形式,即“抽屉原理”。
(3)运用原理,得出在某个“抽屉”中至少分放物体的个数,最终归到原题结论上。
4.温馨提示:要把a个物体放进n个抽屉,如果a÷n=b……c(c≠0且c<b),那么一定有一个抽屉至少可以放(b+1)个物体,而不是(b+c)个。
第六单元:整理和复习1 数与代数数的意义及分类1.整数的含义:像……-3,-2,-1,0,1,2,3,……这样的数统称整数。
整数的个数是无限的。
没有最小的整数,也没有最大的整数。
自然数是整数的一部分。


人教版新课标六年级数学下册(1~3单元)重点知识归纳第一单元:负数1.(1)正、负数的读写方法:○1写正数时,加“+”号或省略“+”号两种形式都可以,但是读正数时,加“+”的,一定要读出“正”字;省略“+”号的,这个“正”字也要省略不读。
○2写负数时,一定要写出“一”号,读时也一定要读出“负”字。
(2)0既不是正数,也不是负数,它是正数与负数的分界点。
2.正、负数不能凭正、负号进行区分,比如“+(一3)”是一个负数,而一(一3)却是一个正数。
3.能表示出正数、0、负数的直线,我们把它叫做数轴。
4.(1)数轴的概念:规定了原点、正方向和单位长度的直线叫做数轴。
(2)温度计也可以看作是一数轴。
5.(1)在数轴上,从左到右的顺序就是数从小到大的顺序。
(2)所有的负数都在0的左边,即负数都比0小;所有的正数都在0的右边,即正数都比0大。
因此,负数都比正数小。
(3)比较两个负数的大小,可以先比较与其对应的两个正数的大小,对应的正数大的那个负数反而小。
6.温馨提示:水结冰时的温度是0摄氏度,0在这里的意义不是表示“没有”,而是一个具体的数。
7.温馨提示:在用正负数表示具有相反意义的量时,要先规定哪个量为正(或负)。
如果上升用正数表示,那么下降一定用负数表示。
8.负数与正数相加,如果负数中负号后面的数比正数大,那么得数为负数,式中负号后面的数减去正数得几,结果就是负几。
第二单元:圆柱与圆锥1.圆柱是由两个底面和一个侧面三部分组成的。
2.(1)圆柱的两个圆面叫做底面。
(2)底面各部分的名称:圆柱的底面圆的圆心、半径、直径和周长分别叫做圆柱的底面圆心、底面半径、底面直径和底面周长。
(3)底面的特征:圆柱底面是完全相同的两个圆。
3.(1)圆柱周围的面叫做侧面。
(2)特征:圆柱的侧面是曲面。
4.(1)圆柱两个底面之间的距离叫做圆柱的高。
(2)一个圆柱有无数条高。
5.把圆柱平行于底面进行切割,切面是和底面大小相同的两个圆;把圆柱沿底面直径垂直于底面进行切割,切面是两个完全相同的长方形。
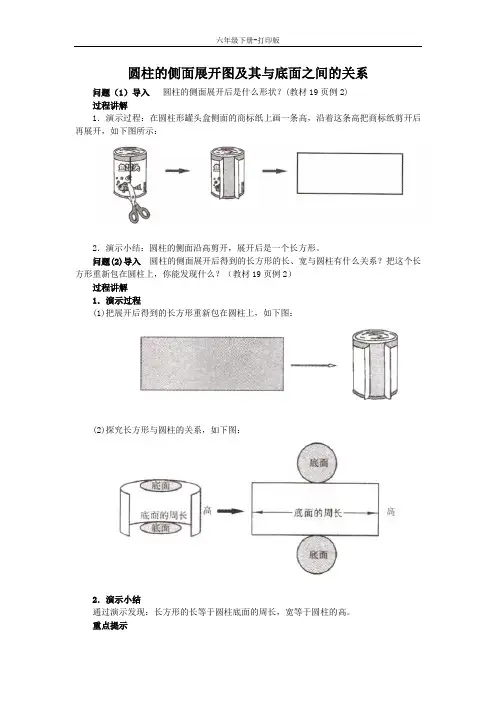
圆柱的侧面展开图及其与底面之间的关系
问题(1)导入圆柱的侧面展开后是什么形状?(教材19页例2)
过程讲解
1.演示过程:在圆柱形罐头盒侧面的商标纸上画一条高,沿着这条高把商标纸剪开后再展开,如下图所示:
2.演示小结:圆柱的侧面沿高剪开,展开后是一个长方形。
问题(2)导入圆柱的侧面展开后得到的长方形的长、宽与圆柱有什么关系?把这个长方形重新包在圆柱上,你能发现什么?(教材19页例2)
过程讲解
1.演示过程
(1)把展开后得到的长方形重新包在圆柱上,如下图:
(2)探究长方形与圆柱的关系,如下图:
2.演示小结
通过演示发现:长方形的长等于圆柱底面的周长,宽等于圆柱的高。
重点提示
当圆柱的底面周长和高相等时,沿高剪开的侧面展开后是一个正方彤。
归纳总结
圆柱的侧面沿高剪开的展开图是一个长方形(或正方形),这个长。
方形(或正方形)的长(或边长)等于圆柱的底面周长,宽(或边长)等于圆柱的商。

六年级数学下册(1~3单元)重点知识归纳第一单元:负数1.(1)正、负数的读写方法:○1写正数时,加“+”号或省略“+”号两种形式都可以,但是读正数时,加“+”的,一定要读出“正”字;省略“+”号的,这个“正”字也要省略不读。
○2写负数时,一定要写出“一”号,读时也一定要读出“负”字。
(2)0既不是正数,也不是负数,它是正数与负数的分界点。
2.正、负数不能凭正、负号进行区分,比如“+(一3)”是一个负数,而一(一3)却是一个正数。
3.能表示出正数、0、负数的直线,我们把它叫做数轴。
4.(1)数轴的概念:规定了原点、正方向和单位长度的直线叫做数轴。
(2)温度计也可以看作是一数轴。
5.(1)在数轴上,从左到右的顺序就是数从小到大的顺序。
(2)所有的负数都在0的左边,即负数都比0小;所有的正数都在0的右边,即正数都比0大。
因此,负数都比正数小。
(3)比较两个负数的大小,可以先比较与其对应的两个正数的大小,对应的正数大的那个负数反而小。
6.温馨提示:水结冰时的温度是0摄氏度,0在这里的意义不是表示“没有”,而是一个具体的数。
7.温馨提示:在用正负数表示具有相反意义的量时,要先规定哪个量为正(或负)。
如果上升用正数表示,那么下降一定用负数表示。
8.负数与正数相加,如果负数中负号后面的数比正数大,那么得数为负数,式中负号后面的数减去正数得几,结果就是负几。
第二单元:圆柱与圆锥1.圆柱是由两个底面和一个侧面三部分组成的。
2.(1)圆柱的两个圆面叫做底面。
(2)底面各部分的名称:圆柱的底面圆的圆心、半径、直径和周长分别叫做圆柱的底面圆心、底面半径、底面直径和底面周长。
(3)底面的特征:圆柱底面是完全相同的两个圆。
3.(1)圆柱周围的面叫做侧面。
(2)特征:圆柱的侧面是曲面。
4.(1)圆柱两个底面之间的距离叫做圆柱的高。
(2)一个圆柱有无数条高。
5.把圆柱平行于底面进行切割,切面是和底面大小相同的两个圆;把圆柱沿底面直径垂直于底面进行切割,切面是两个完全相同的长方形。


六年级数学下册(1~3单元)重点知识归纳第一单元:负数1.《1》正;负数的读写方法:○1写正数时,加“+”号或省略“+”号两种形式都可以,但是读正数时,加“+”的,一定要读出“正”字;省略“+”号的,这个“正”字也要省略不读。
○2写负数时,一定要写出“一”号,读时也一定要读出“负”字。
《2》0既不是正数,也不是负数,它是正数与负数的分界点。
2.正;负数不能凭正;负号进行区分,比如“+《一3》”是一个负数,而一《一3》却是一个正数。
3.能表示出正数;0;负数的直线,我们把它叫做数轴。
4.《1》数轴的概念:规定了原点;正方向和单位长度的直线叫做数轴。
《2》温度计也可以看作是一数轴。
5.《1》在数轴上,从左到右的顺序就是数从小到大的顺序。
《2》所有的负数都在0的左边,即负数都比0小;所有的正数都在0的右边,即正数都比0大。
因此,负数都比正数小。
《3》比较两个负数的大小,可以先比较与其对应的两个正数的大小,对应的正数大的那个负数反而小。
6.温馨提示:水结冰时的温度是0摄氏度,0在这里的意义不是表示“没有”,而是一个具体的数。
7.温馨提示:在用正负数表示具有相反意义的量时,要先规定哪个量为正《或负》。
如果上升用正数表示,那么下降一定用负数表示。
8.负数与正数相加,如果负数中负号后面的数比正数大,那么得数为负数,式中负号后面的数减去正数得几,结果就是负几。
第二单元:圆柱与圆锥1.圆柱是由两个底面和一个侧面三部分组成的。
2.《1》圆柱的两个圆面叫做底面。
《2》底面各部分的名称:圆柱的底面圆的圆心;半径;直径和周长分别叫做圆柱的底面圆心;底面半径;底面直径和底面周长。
《3》底面的特征:圆柱底面是完全相同的两个圆。
3.《1》圆柱周围的面叫做侧面。
《2》特征:圆柱的侧面是曲面。
4.《1》圆柱两个底面之间的距离叫做圆柱的高。
《2》一个圆柱有无数条高。
5.把圆柱平行于底面进行切割,切面是和底面大小相同的两个圆;把圆柱沿底面直径垂直于底面进行切割,切面是两个完全相同的长方形。

北师大版六年级数学下册知识点第一单元《圆柱与圆锥》知识点点动成线,线动成面,面动成体。
圆柱的上、下两个面叫做圆柱的底面。
它们是大小相等的两个圆。
侧面是一个曲面。
沿圆柱的高剪开,圆柱的侧面展开图是一个长方形或正方形(底面周长和高相等时,展开是一个正方形),如果斜着剪,圆柱的侧面展开图是平行四边形。
圆柱两个底面之间的距离叫做高,圆柱有无数条高。
圆锥只有一个底面,是一个圆形。
侧面是一个曲面,圆锥侧面展开是一个扇形。
圆锥的顶点到底面圆心的距离是圆锥的高,圆锥只有一条高。
把圆柱沿底面直径切开,切面是长方形或正方形。
当底面直径与高相等时是正方形。
把圆柱垂直于高切下去,切面是个圆形。
把圆锥沿高切下去,切面是个三角形。
圆柱的侧面积=底面周长×高,字母公式是S=Ch=πdh=2πrh 。
C=S ÷h h=S ÷C圆柱的表面积=侧面积+底面积,在计算时要注意它有几个底面。
圆柱的体积=底面积×高,字母公式是V=Sh=πr 2 h S=V ÷h h=V ÷S圆柱的体积等于和它等底等高的圆锥体积的3倍。
圆锥体积=31×底面积×高 V=31Sh S=V ×3÷h h=V ×3÷S第二单元《比例》知识点表示两个比相等的式子叫作比例。
两端的两项叫作比例的外项,中间的两项叫作比例的内项在比例里,两个内项的积等于两个外项的积。
图上距离和实际距离的比,叫作这幅图的比例尺。
比例尺是一个最简单的整数比,它没有计量单位,也不能是一个具体的数。
图上距离︰实际距离=比例尺 图上距离=实际距离×比例尺实际距离=图上距离÷比例尺比例尺的分类:按形式分,分为线段比例尺和数值比例尺。
按用途分,分为缩小比例尺和放大比例尺。
图形放大前后对应线段长的比相等。
图形缩小前后对应线段长的比相等。
放大或者缩小,只改变图形的大小,不改变图形的形状。
第一单元负数1、负数的由来:为了表示相反意义的两个量(如盈利亏损、收入支出……),光有学过的 0 1 3.4 2/5……是远远不够的。
所以出现了负数,以盈利为正、亏损为负;以收入为正、支出为负2、负数:小于 0 的数叫负数(不包括 0),数轴上 0 左边的数叫做负数。
若一个数小于 0,则称它是一个负数。
负数有无数个,其中有(负整数,负分数和负小数)负数的写法:数字前面加负号“-”号,不可以省略例如:-2,-5.33,-45,-2/53、正数:大于 0 的数叫正数(不包括 0),数轴上 0 右边的数叫做正数若一个数大于 0,则称它是一个正数。
正数有无数个,其中有(正整数,正分数和正小数)正数的写法:数字前面可以加正号“+”号,也可以省略不写。
例如:+2,5.33,+45,2/54、0 既不是正数,也不是负数,它是正、负数的分界限负数都小于 0,正数都大于 0,负数都比正数小,正数都比负数大5、数轴:6、比较两数的大小:①利用数轴:负数<0<正数或左边<右边②利用正负数含义:正数之间比较大小,数字大的就大,数字小的就小。
负数之间比较大小,数字大的反而小,数字小的反而大1/3>1/6 -1/3<-1/6第二单元百分数二(一)、折扣和成数1、折扣:用于商品,现价是原价的百分之几,叫做折扣。
通称“打折”。
几折就是十分之几,也就是百分之几十。
例如:八折=8/10=80﹪,六折五=6.5/10=65/100=65﹪解决打折的问题,关键是先将打的折数转化为百分数或分数,然后按照求比一个数多(少)百分之几(几分之几)的数的解题方法进行解答。
商品现在打八折:现在的售价是原价的 80﹪商品现在打六折五:现在的售价是原价的 65﹪2、成数:几成就是十分之几,也就是百分之几十。
例如:一成=1/10=10﹪八成五=8.5/10=85/100=80﹪解决成数的问题,关键是先将成数转化为百分数或分数,然后按照求比一个数多(少)百分之几(几分之几)的数的解题方法进行解答。
人教版小学数学六年级下册16单元知识点思维导图一、数与代数1. 分数分数的意义和性质分数加减法分数乘除法分数混合运算2. 小数小数的意义和性质小数加减法小数乘除法小数混合运算3. 比和比例比的意义和性质比例的意义和性质比例尺比例应用题二、空间与图形1. 角角的度量角的分类角的画法2. 三角形三角形的性质三角形的分类三角形的画法3. 四边形四边形的性质四边形的分类四边形的画法4. 圆圆的性质圆的画法圆的周长和面积三、统计与概率1. 数据的收集和整理调查法抽样调查数据整理2. 数据的表示条形统计图折线统计图扇形统计图3. 数据的分析平均数中位数众数4. 概率概率的定义概率的计算概率应用题四、实践与综合应用1. 实践活动数学游戏数学实验数学探究2. 综合应用解决实际问题的能力综合应用题数学建模人教版小学数学六年级下册16单元知识点思维导图一、数与代数1. 分数分数的意义和性质分数表示部分与整体的关系分数的分子和分母分数的基本性质分数加减法同分母分数的加减法异分母分数的加减法分数加减法的应用分数乘除法分数乘法的意义和计算方法分数除法的意义和计算方法分数乘除法的应用分数混合运算分数混合运算的顺序分数混合运算的技巧分数混合运算的应用2. 小数小数的意义和性质小数表示部分与整体的关系小数的整数部分和小数部分小数的基本性质小数加减法小数点对齐的加减法小数加减法的应用小数乘除法小数乘法的意义和计算方法小数除法的意义和计算方法小数乘除法的应用小数混合运算小数混合运算的顺序小数混合运算的技巧小数混合运算的应用3. 比和比例比的意义和性质比表示两个数的关系比的基本性质比例的意义和性质比例表示两个比的关系比例的基本性质比例尺比例尺的定义比例尺的应用比例应用题比例问题的解决方法比例问题的应用二、空间与图形1. 角角的度量角的定义角的度量单位角的分类锐角、直角、钝角、周角角的画法角的画法步骤角的画法应用2. 三角形三角形的性质三角形的边和角的关系三角形的分类三角形的分类按边分类:等边三角形、等腰三角形、不等边三角形按角分类:锐角三角形、直角三角形、钝角三角形三角形的画法三角形的画法步骤三角形的画法应用3. 四边形四边形的性质四边形的边和角的关系四边形的分类四边形的分类按边分类:等边四边形、等腰四边形、不等边四边形按角分类:锐角四边形、直角四边形、钝角四边形四边形的画法四边形的画法步骤四边形的画法应用4. 圆圆的性质圆的定义圆的基本性质圆的画法圆规的使用方法圆的画法应用圆的周长和面积圆的周长公式圆的面积公式三、统计与概率1. 数据的收集和整理调查法调查问卷的设计调查数据的收集抽样调查抽样调查的方法抽样调查的应用数据整理数据的排序数据的分组2. 数据的表示条形统计图条形统计图的制作条形统计图的应用折线统计图折线统计图的制作折线统计图的应用扇形统计图扇形统计图的制作扇形统计图的应用3. 数据的分析平均数平均数的计算方法平均数的应用中位数中位数的计算方法中位数的应用众数众数的计算方法众数的应用4. 概率概率的定义概率的计算方法概率的表示概率的计算概率的基本公式概率的计算应用概率应用题概率问题的解决方法概率问题的应用四、实践与综合应用1. 实践活动数学游戏数学游戏的设计数学游戏的规则数学实验数学实验的设计数学实验的操作数学探究数学探究的主题数学探究的方法2. 综合应用解决实际问题的能力实际问题的分析实际问题的解决综合应用题综合应用题的类型综合应用题的解答数学建模数学建模的意义数学建模的方法人教版小学数学六年级下册16单元知识点思维导图一、数与代数1. 分数分数的意义和性质分数表示部分与整体的关系分数的分子和分母分数的基本性质分数加减法同分母分数的加减法异分母分数的加减法分数加减法的应用分数乘除法分数乘法的意义和计算方法分数除法的意义和计算方法分数乘除法的应用分数混合运算分数混合运算的顺序分数混合运算的技巧分数混合运算的应用2. 小数小数的意义和性质小数表示部分与整体的关系小数的整数部分和小数部分小数的基本性质小数加减法小数点对齐的加减法小数加减法的应用小数乘除法小数乘法的意义和计算方法小数除法的意义和计算方法小数乘除法的应用小数混合运算小数混合运算的顺序小数混合运算的技巧小数混合运算的应用3. 比和比例比的意义和性质比表示两个数的关系比的基本性质比例的意义和性质比例表示两个比的关系比例的基本性质比例尺比例尺的定义比例尺的应用比例应用题比例问题的解决方法比例问题的应用二、空间与图形1. 角角的度量角的定义角的度量单位角的分类锐角、直角、钝角、周角角的画法角的画法步骤角的画法应用2. 三角形三角形的性质三角形的边和角的关系三角形的分类三角形的分类按边分类:等边三角形、等腰三角形、不等边三角形按角分类:锐角三角形、直角三角形、钝角三角形三角形的画法三角形的画法步骤三角形的画法应用3. 四边形四边形的性质四边形的边和角的关系四边形的分类四边形的分类按边分类:等边四边形、等腰四边形、不等边四边形按角分类:锐角四边形、直角四边形、钝角四边形四边形的画法四边形的画法步骤四边形的画法应用4. 圆圆的性质圆的定义圆的基本性质圆的画法圆规的使用方法圆的画法应用圆的周长和面积圆的周长公式圆的面积公式三、统计与概率1. 数据的收集和整理调查法调查问卷的设计调查数据的收集抽样调查抽样调查的方法抽样调查的应用数据整理数据的排序数据的分组2. 数据的表示条形统计图条形统计图的制作条形统计图的应用折线统计图折线统计图的制作折线统计图的应用扇形统计图扇形统计图的制作扇形统计图的应用3. 数据的分析平均数平均数的计算方法平均数的应用中位数中位数的计算方法中位数的应用众数众数的计算方法众数的应用4. 概率概率的定义概率的计算方法概率的表示概率的计算概率的基本公式概率的计算应用概率应用题概率问题的解决方法概率问题的应用四、实践与综合应用1. 实践活动数学游戏数学游戏的设计数学游戏的规则数学实验数学实验的设计数学实验的操作数学探究数学探究的主题数学探究的方法2. 综合应用解决实际问题的能力实际问题的分析实际问题的解决综合应用题综合应用题的类型综合应用题的解答数学建模数学建模的意义数学建模的方法。
六年级上册这一册教材包括下面一些内容:位置,分数乘法,分数除法,圆,百分数,统计,数学广角和数学实践活动等。
分数乘法和除法,圆,百分数等是本册教材的重点教学内容。
在数与代数方面,这一册教材安排了分数乘法、分数除法、百分数三个单元。
分数乘法和除法的教学是在前面学习整数、小数有关计算的基础上,培养学生分数四则运算能力以及解决有关分数的实际问题的能力。
分数四则运算能力是学生进一步学习数学的重要基本技能,应该让学生切实掌握。
百分数在实际生活中有着广泛的应用,理解百分数的意义、掌握百分数的计算方法,会解决简单的有关百分数的实际问题,也是小学生应具备的基本数学能力。
在空间与图形方面,这一册教材安排了位置、圆两个单元。
位置的教学在已有知识和经验的基础上,通过丰富的现实的数学活动,让学生经历初步的数学化的过程,理解并学会用数对表示位置;通过对曲线图形——圆的特征和有关知识的探索与学习,初步认识研究曲线图形的基本方法,促进学生空间观念的进一步发展。
在统计方面,本册教材安排的是扇形统计图。
在前面学习条形统计图和折线统计图的基础上,学会看懂扇形统计图,认识扇形统计图的特点,进一步体会统计在生活和生产实际当中的运用在用数学解决问题方面,教材一方面结合分数乘法和除法、百分数、圆、统计等知识,教学用所学的知识解决生活中的简单问题;另一方面,安排了“数学广角”的教学内容,引导学生通过观察、猜测、实验、推理等活动,体会解决问题策略的多样性及运用假设的方法解决问题的有效性,进一步体会用代数方法解决问题的优越性,感受数学的魅力,发展学生解决问题的能力。
六年级上册一、位置 (用数对表示具体情境中物体的位置;在方格纸上用数对确定物体的位置。
)二、分数乘法 (分数乘法;整数乘法运算定律推广到分数乘法运算中;求一个数的几分之几是多少的实际问题;倒数。
)三、分数除法 (分数除法;已知一个数的几分之几是多少求这个数的实际问题;比的意义,比与分数、除法的关系,比的基本性质,化简比和求比值;运用比的知识解决有关的实际问题。