2018年河北省衡水市冀州中学高一

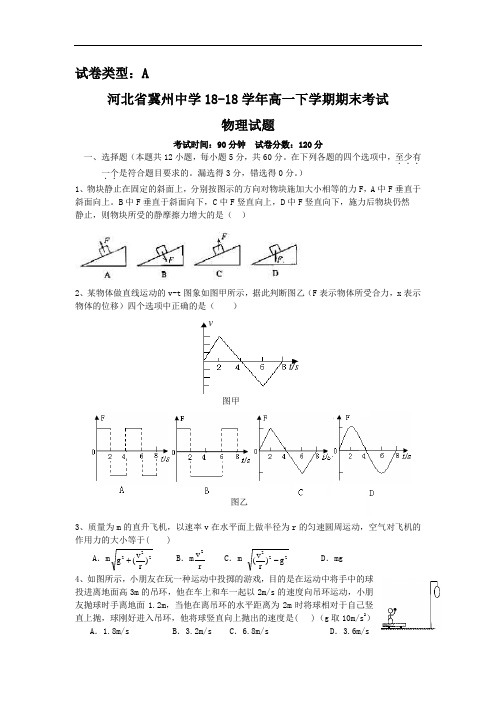
试卷类型：A河北省冀州中学18-18学年高一下学期期末考试物理试题考试时间：90分钟 试卷分数：120分一、选择题（本题共12小题，每小题5分，共60分。

在下列各题的四个选项中，至少有．．．一个．．是符合题目要求的。

漏选得3分，错选得0分。

） 1、物块静止在固定的斜面上，分别按图示的方向对物块施加大小相等的力F ，A 中F 垂直于 斜面向上。

B 中F 垂直于斜面向下，C 中F 竖直向上，D 中F 竖直向下，施力后物块仍然 静止，则物块所受的静摩擦力增大的是（ ）2、某物体做直线运动的v-t 图象如图甲所示，据此判断图乙（F 表示物体所受合力，x 表示物体的位移）四个选项中正确的是（ ）答案：B3、质量为m 的直升飞机，以速率v 在水平面上做半径为r 的匀速圆周运动，空气对飞机的作用力的大小等于( )A ．m 222)r v (g + B ．m r v 2C ．m 222g )rv (- D ．mg4、如图所示，小朋友在玩一种运动中投掷的游戏，目的是在运动中将手中的球投进离地面高3m 的吊环，他在车上和车一起以2m/s 的速度向吊环运动，小朋友抛球时手离地面1.2m ，当他在离吊环的水平距离为2m 时将球相对于自己竖直上抛，球刚好进入吊环，他将球竖直向上抛出的速度是( )（g 取10m/s 2） A ．1.8m/s B ．3.2m/s C ．6.8m/s D ．3.6m/sv t/s 图甲 图乙5、2018年9月25日至28日我国成功实施了“神舟”七号载入航天飞行并实现了航天员首次出舱。

飞船先沿椭圆轨道飞行，后在远地点343千米处点火加速，由椭圆轨道变成高度为343千米的圆轨道，在此圆轨道上飞船运行周期约为90分钟。

下列判断正确的是（ ） A ．飞船变轨前后的机械能相等B ．飞船在圆轨道上时航天员出舱前后都处于失重状态C ．飞船在此圆轨道上运动的角度速度大于同步卫星运动的角速度D ．飞船变轨前通过椭圆轨道远地点时的加速度大于变轨后沿圆轨道运动的加速度 6、某质点做简谐运动，其位移随时间变化的关系式为x ＝Asin 4t，则质点( ) A.第1 s 末与第3 s 末的加速度相同B.第1 s 末与第3 s 末的动量相同C.3 s 末至5 s 末的位移方向都相同D.3 s 末至5 s 末的速度方向都相同7、如图所示，倾斜的传送带保持静止，一木块从顶端以一定的初速度匀加速下滑到底端．如果让传送带沿图中虚线箭头所示的方向匀速运动，同样的木块从顶端以同样的初速度下滑到底端的过程中，与传送带保持静止时相比 ( )A ．木块在滑到底端的过程中，摩擦力的冲量变大B ．木块在滑到底端的过程中，摩擦力的冲量不变C ．木块在滑到底端的过程中，木块克服摩擦力所做的功变大D ．木块在滑到底端的过程中，系统产生的内能数值将不变8、为了安全，汽车在行驶途中，车与车之间必须保持一定的距离，这是因为从驾驶员看见某一情况到采取制动动作的反应时间里，汽车仍然要通过一段距离（称为反应距离），而从采取制动动作到汽车停下的时间内，汽车也要通过一段距离，称为制动距离，下表中列出了在不同速度下的反应距离和制动距离的部分数据，根据分析计算，表中未给出的数据X 、Y 应是：( ) A ．X=40，Y=24 B ．X=45，Y=24C ．X=50，Y=22D ．X=60，Y=229、如图1所示，水平面上质量均为5kg 的两木块A 、B平衡状态。

试卷类型:A 卷 河北冀州中学 2018—2018学年度下学期期中考试高一年级物理（理）试题考试时间90分钟 试题分数120分注意事项：1.答题前，务必将自己的班级、姓名、学号填写在答题纸规定的位置上。

2.答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其他答案标号。

3.答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题纸规定的位置上。

4.所有题目必须在答题纸上作答，在试题卷上答题无效。

I 卷一、选择题（本题共12小题，每小题6分，漏选得3分，多选、错选不得分。

共72分。

）1、一个物体做变速运动，下列叙述中正确的是（ ）A ．物体所受的合外力一定为变力B ．合外力一定对物体做功，物体的动能一定改变C ．合外力不一定对物体做功，物体的动能不一定改变D ．合外力一定不为零，物体的速度一定改变2、平抛物体的初速度为v 0，当水平方向分位移与竖直方向分位移相等时（ ） A.运动的时间02v t g=B．瞬时速率0t vC.水平分速度与竖直分速度大小相等D.位移大小等于20/g3、在下列几种运动中，遵守机械能守恒定律的运动是 （ ） A.自由落体运动 B.雨点匀速下落 C.物体沿光滑斜面下滑 D.汽车刹车的运动4、质量为m 的物体沿着半径为r 的半球形金属球壳滑到最低点时的速度大小为υ，如图所示，若物体与球壳之间的摩擦因数为μ，则物体在最低点时的 （ ）A ．向心加速度为υ2rB ．向心力为m （g +υ2r ）C ．对球壳的压力为mυ2r D ．受到的摩擦力为μm （g +υ2r）5．火星有两颗卫星，分别是火卫一和火卫二，它们的轨道近似为圆。

已知火卫一的周期为7h39min ，火卫二的周期为30h18min 。

则两颗卫星相比（ ） A 、火卫一距火星表面较近 B 、火卫二的角速度较大 C 、火卫一的运动速度较大 D 、火卫二的向心加速度较大 6．做曲线运动的物体，在运动过程中，一定变化的物理量是（ ） A ．速率 B ．速度 C ．加速度 D ．合力r7、下列说法中正确的是： （ ）A.摩擦力一定对物体做负功B.静摩擦力一定不做功C.滑动摩擦力可以对物体不做功D.静摩擦力的方向可以跟物体运动方向垂直 8．一质量为m 的木块静止在光滑的水平面上，从t=0开始，将一个大小为F 的水平恒力作用在该木块上，在t=t 1时刻F 的功率是（ ）A ．F 2t 1/mB ．F 2t 12/2mC ．F 2t 1/2mD ．F 2t 12/m 9．起重机竖直吊起质量为m 的重物，上升的加速度是α，上升的高度是h ，则起重机对货物所做的功是。

试卷类型A 河北冀州中学2018—2018学年度下学期期末考试高一年级化学试题考试时间90分钟试题分数110分可能用到的相对原子质量：H－1 C－12 N－14 O－16 Na－23 Cl－35.5 Cu－64Ⅰ卷（50分）一、选择题（每题只有一个．．．．正确选项，1-10每小题2分，11-20每小题3分）1．2018年诺贝尔化学奖得主Gerhard Ertl对金属Pt表面催化CO氧化反应的模型进行了深入研究。

下列关于20278Pt的说法正确的是（）A．20278Pt和19878Pt的质子数相同，互称为同位素B．20278Pt和19878Pt的中子数相同，互称为同位素C．20278Pt和19878Pt的核外电子数相同，是同一种核素D．20278Pt和19878Pt的质量数不同，不能互称为同位素2．开发新材料是现代科技发展的方向之一。

下列有关材料的说法正确的是（）A．氮化硅陶瓷是新型无机非金属材料B．C60属于一种新型化合物，用于制造纳米材料C．单晶硅常用于制造光导纤维D．世界上现在已经成功研制了液氮动力车，其工作原理是：氮气是一种可燃性气体，燃烧时放热。

3．下列关于臭氧性质的叙述中不正确的是（）A．臭氧比氧气的氧化性更强，常温下能将Ag、Hg等较不活泼的金属氧化B．臭氧可以杀死许多细菌，是一种良好的消毒剂C．O2比O3稳定D．臭氧和氧气在一定条件下可以相互转化，是物理变化4．下列金属能溶于稀硫酸，但用它制成的容器可用来盛装浓硫酸的是（）A．锌B．铁C．铜D．金5．可以说明硫比氯气氧化性弱的是( )A．常温下硫为固体而氯气是气体B．硫不溶于水而氯气溶于水C．与Fe反应，硫被还原为－2价，而氯被还原为－1价D．Fe与S反应生成FeS而与Cl2反应生成FeCl36．下列叙述中正确的是（）A．NH3、CO、CO2都是极性分子B．CH4、CCl4都是含有极性键的非极性分子C．HF、HCl、HBr、HI的稳定性依次增强D．CS2、H2O、CO2都是直线型分子7．下列有关试剂的保存，错误的是（）A．少量白磷保存在水中（冷水）B．金属钠要保存在煤油里C．氢氟酸要保存在橡胶塞的玻璃瓶中D．浓硝酸要保存在棕色试剂瓶中8．通过实验观察，得知某气体有下列性质：①无色有刺激性气味；②潮湿空气中形成雾；③易溶于水，溶液使石蕊试纸变红；④把它加入浓HNO3中，产生红棕色气体。

2017-2018学年河北省衡水市冀州中学高一（上）期中物理试卷一、选择题（本题共20小题，每小题3分，共60分。

1-13为单选题，在每小题给出的四个选项中只有一个选项正确，14-20为多选题，错选不得分少选得2分）1．（3分）关于质点下列说法正确的是（）A．质点一定是体积很小的物体B．只有做直线运动的物体才可以看成质点C．如果物体上各点的运动情况完全相同，在研究物体的运动速度随时间的变化规律时可以将物体看成质点D．研究奥运会三米跳板运动员的跳水动作时，可以把她看作质点2．（3分）小球从离地面高为2m处竖直向上抛出，上升0.5m后又落到地面上停下，规定向上为正，则小球运动的全过程中通过的路程和位移分别为（）A．3m，2m B．﹣3m，﹣2m C．3m，﹣2m D．﹣3m，2m3．（3分）一个物体受到敲击后，沿倾角为θ的光滑斜面底端向上滑行，则上滑过程中，物体受力情况为（）A．重力：垂直斜面向下，弹力：垂直斜面指向被支持物体B．重力：竖直向下，弹力：垂直斜面指向被支持物体C．重力：竖直向下，冲力：沿斜面向上，弹力：垂直斜面指向被支持物体D．重力：竖直向下，弹力：垂直斜面向上，下滑力：沿斜面向下，冲力：沿斜面向上4．（3分）对于公式v t=v0+at，下列说法中正确的是（）A．适用于任何变速运动B．只适用于匀加速直线运动C．适用于任何匀变速直线运动D．v0和v t只能取正值，不可能为负值5．（3分）一轻质弹簧一端固定，用大小为F1的力压弹簧的另一端，平衡时弹簧长度为l1；若改用大小为F2的力拉弹簧的另一端，平衡时弹簧长度为l2，已知弹簧的拉伸或压缩均在弹性限度内，则该弹簧的劲度系数为（）A．B．C．D．6．（3分）关于重力与重心下列说法正确的是（）A．物体在空中下落时受到的重力比静止时受到的重力大B．规则物体的重心一定在其几何中心C．放在桌面上的物体对桌面的压力，其实就是该物体的重力D．重心是物体内各部分所受的重力的合力的等效作用点7．（3分）小球从空中自由下落，与水平地面相碰后弹到空中某一高度，其速度﹣时间图象如图所示，则由图可知（g取10m/s2）（）A．小球下落的高度2.5mB．小球在从开始下落0.8s内的平均速度大小是4m/s，方向竖直向下C．小球在从开始下落0.8s内的位移为0.8m，方向竖直向下D．小球在从开始下落0.5s内和后0.3s内加速度大小相等，方向相同8．（3分）如图所示，直线a和曲线b分别是在平直公路上行驶的汽车a和b的位置﹣时间（x﹣t）图线．由图可知（）A．在时刻t2，a、b两车运动方向相反B．在时刻t1、a车追上b车C．在t1到t2这段时间内，b车的位移比a车的大D．在t1到t2这段时间内，b车的速率一直比a车的大9．（3分）已知力F的一个分力F1跟F成30°角，大小未知，另一分力F2的大小为，方向未知。

2018-2018学年河北省衡水市冀州中学高一（下）开学物理试卷一、单项选择题（共10小题，每小题2分，满分20分）1．一个小石块从空中a点自由落下，先后经过b点和c点．不计空气阻力．已知它经过b点时的速度为v，经过c点时的速度为3v．则ab段与bc段位移之比为（）A．1：3 B．1：5 C．1：8 D．1：92．某质点从静止开始做匀加速直线运动，已知第3秒内通过的位移是x，则物体运动的加速度为（）A．B．C．D．3．如图所示，固定在竖直平面内的光滑圆环的最高点有一个光滑的小孔，质量为m的小球套在圆环上，一根细线的下端系着小球，上端穿过小孔用手拉住，现拉动细线，使小球沿圆环缓慢上移，在移动过程中手对线的拉力F和轨道对小球的弹力N的大小变化情况是（）A．F减小，N不变B．F不变，N减小C．F不变，N增大D．F增大，N减小4．在水平的足够长的固定木板上，一小物块以某一初速度开始滑动，经一段时间t后停止．现将该木板改置成倾角为45°的斜面，让小物块以相同的初速度沿木板上滑．若小物块与木板之间的动摩擦因数为μ．则小物块上滑到最高位置所需时间与t之比为（）A．B．C．D．5．如图，在光滑的水平桌面上有一物体A，通过绳子与物体B相连，假设绳子的质量以及绳子与定滑轮之间的摩擦力都可以忽略不计，绳子不可伸长．如果m B=3m A，则物体A的加速度大小等于（）A．3g B．g C．D．6．如图所示，有两个相同材料物体组成的连接体在斜面上运动，当作用力F一定时，m2所受绳的拉力（）A．与θ无关B．与斜面动摩擦因数无关C．与系统运动状态有关D．F T=，仅与两物体质量有关7．如图所示，一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上．物体与斜面接触时速度与水平方向的夹角φ满足（）A．tanφ=sinθB．tanφ=cosθC．tanφ=tanθD．tanφ=2tanθ8．一条笔直的河流，宽l=40m，水的流速是v1=3m/s，有航速（相对水面）为v2=4m/s的小汽船保持船身垂直河岸渡到彼岸．则小汽船渡河的时间和位移（相对地面）分别为（）A．8s，30m B．8s，40m C．10s，30m D．10s，50m9．在水平面上，小猴拉着小滑块做匀速圆周运动，O点为圆心，能正确地表示小滑块受到的牵引力F及摩擦力F f的图是（）A．B．C．D．10．如图所示，有一个半径为R的光滑圆轨道，现给小球一个初速度，使小球在竖直面内做圆周运动，则关于小球在过最高点的速度v，下列叙述中正确的是（）A．v的极小值为B．v由零逐渐增大，轨道对球的弹力逐渐增大C．当v由值逐渐增大时，轨道对小球的弹力也逐渐增大D．当v由值逐渐减小时，轨道对小球的弹力也逐渐减小二、多项选择题（共15小题，每小题3分，满分45分。

冀州中学 2018—2018高一物理文期末考试一、选择题（每小题2分，共28分；每小题给出的四个选项中，只有一个选项符合题意，有选错或不答的得0分。

）1.关于惯性，下列说法中正确的是（）A. 静止的物体没有惯性B. 速度越大的物体惯性越大C. 同一物体在地球上和月球上惯性不同D. 质量越大的物体惯性越大2. 在研究下列问题中，能够把研究对象看作质点的是（）A．研究地球的自转B．研究地球绕太阳的公转C．研究一列火车通过某一路标所用的时间D．研究乒乓球的旋转3. 关于物体的重心，下列说法中正确的是（）A. 任何物体的重心都一定在这个物体上B. 重心的位置只与物体的形状有关C.形状规则、质量分布均匀的物体，其重心在物体的几何中心D. 物体重心的位置一定会随物体形状改变而改变4. 关于速度与加速度的关系，下列说法中正确的是（）A. 物体的速度改变越快，其加速度也越大B. 物体的速度越大，其加速度也越大C. 物体的速度改变量越大，其加速度也越大D. 物体的速度为零，其加速度一定为零5. 如图所示为某校学生开展无线电定位“搜狐”比赛，甲、乙两人从O点同时出发，并同时到达A点搜到狐狸，两人的搜狐路径已在图中标出，则（）A.甲的平均速度大于乙的平均速度B. 两人运动的平均速度相等C. 甲的位移大于乙的位移D. 甲的路程等于乙的路程6．洗衣机的脱水筒采用带动衣物旋转的方式脱水，下列说法中错误的是（）A脱水过程中，衣物是紧贴筒壁的B加快脱水筒转动角速度，脱水效果会更好C水会从桶中甩出是因为水滴受到向心力很大的缘故D靠近中心的衣物脱水效果不如四周的衣物脱水效果好7. 如上图所示小物体A与圆盘保持相对静止，跟着圆盘一起做圆周运动，则A 的受力情况是（）A受重力，支持力B受重力，支持力和指向圆心的摩擦力C受重力，支持力，向心力和指向圆心的摩擦力D以上都不正确。

8．作匀速圆周运动的物体，其加速度的数值必定 （ ） A ．跟其角速度的平方成正比 B ．跟其线速度的平方成正比C ．跟其运动的半径成反比D ．跟其运动的线速度和角速度的乘积成正比9. 下列关于平抛运动及两个分运动的说法不正确的是 （ ） A 某段时间内的合位移等于两分位移的矢量和，某一时刻的合速度等于两分速度的矢量和 B 两个分运动是先后进行的C 水平方向速度大小并不影响物体竖直方向的运动D 两个分运动和合运动在时间上是相等的10．竖直升空的火箭，其v —t 图象如图所示，由图可知以下说法中正确的是 （ ）A. 火箭上升的最大高度为16000mB. 火箭上升的最大高度为48000mC. 火箭经过120s 落回地面D. 火箭上升过程中的加速度始终是20m/s2 11、把木箱放在电梯的水平地板上，则下列运动中地板受到的压力最小的是 （ ）A ．电梯以a =5m/s 2的加速度匀减速上升B ．电梯以a =2m/s 2的加速度匀加速上升C ．电梯以a =2.5m/s 2的加速度匀加速下降D ．电梯以v =10m/s 的速度匀速上升12．如图3所示，A 、B 是两个摩擦传动的靠背轮，A 是主动轮，B 是从动轮，它们的半径R A ＝2R B ， a 和b 两点在轮的边缘，c 和d 在各轮半径的中点，下列判断正确的有（ ）A V a = 2 V bB ωb = 2ωaC V c = V aD ωb = ωc13.以速度v 0水平抛出一球，某时刻其竖直分位移与水平位移相等，以下判断错误的是（ ）（A ）竖直分速度等于水平分速度（B ）此时球的速度大小为5 v 0（C ）运动的时间为g v 02 （D ）运动的竖直位移是22v g14.（6分）汽车刹车后，停止转动的轮胎在地面上发生滑动，产生明显的滑动痕迹，即常说的刹车线。

2017-2018学年河北省衡水市冀州中学高一（下）期末语文试卷副标题一、选择题（本大题共8小题，共24.0分）1.下列各句中加点成语的使用，全都不正确的一项是（）①碧波荡漾的湖水，欢快的鸟声，吐绿的柳条……经过治理开发，这里的生态环境变好了，再加上这里的气候冬温夏清．．．．，使得这里游人不断。

②《乱弹三月》使用了特殊的舞台背景和二胡、笙、箫等乐器，当宣布演出开始，一时间霓虹闪烁，瓦釜雷鸣．．．．，令人耳目一新。

③十余年如一日的刻苦练习，博采众长，使他的书法创作日渐成熟，他既能写出谦和宁静的《心经》，也能呈上洋洋洒洒．．．．的《洛神赋》。

④我们要善于把传统文化的精华内化于心，外化于行，要在践行上下功夫，克服知而不行、首鼠两端．．．．的毛病，而不是喊喊口号。

⑤他的作品充满诗情画意，形神兼备，洋溢着游子浓浓的莼鲈之思．．．．，读来犹如一曲古老的民歌，那高亢的秦腔至今仍让人牵肠挂肚。

⑥《中国诗词大会》成为人们评头论足．．．．的电视节目，相较于近几年博人眼球、追求搞笑效果的各色综艺节目，可谓卓尔不群。

A. ①③⑥B. ①④⑤C. ②③⑤D. ②④⑥【答案】D【解析】①望文生义，冬温夏清：指为人子的孝道。

此处误以为“生态环境好”；②望文生义，瓦釜雷鸣：比喻无才无能的人占据高位，煊赫一时。

此处误以为“各种乐器发出声响”；③正确，洋洋洒洒：形容文章或谈话内容丰富，连续不断，或形容规模、气势盛大。

符合语境；④不合语境，首鼠两端：迟疑不决，动摇不定。

此处强调的是“没有行动”；⑤正确，莼鲈之思：比喻怀念故乡的心情。

符合语境；⑥感情色彩不当，评头论足：指无聊的人随便谈论妇女的容貌，也比喻在小节上多方挑剔。

此处属于贬词褒用；故选：D。

该题考查正确使用成语的能力。

此类题要在理解句意的基础上，结合具体语境及词语的意思从三个方面综合考虑分析即成语的基本义、感情色彩和语境。

需要注意色彩不明，断词取义，对象误用，谦敬错位，功能混乱，不合语境，望文生义等错误使用类型。

2018年冀州中学高一数学下学期期末试题（理科附解析）
5 c 2018学年河北省衡水市冀州中学高一（下）期末数学试卷（理科）
参考答案与试题解析
一、选择题（共15个小题，每小题4分，共60分在每个小题给出的四个选项中，只有一项是符合要求的）
1．已知全集U=R，A= ，B={x|lnx＜0}，则A∪B=（）
A．{x|﹣1≤x≤2}B．{x|﹣1≤x＜2}c．{x|x＜﹣1或x≥2}D．{x|0＜x＜2}
【考点】并集及其运算．
【分析】求出A与B中不等式的解集，分别确定出A与B，找出两集合的并集即可．
【解答】解由A中不等式变形得≤0，即（x+1）（x﹣2）＜0，且x﹣2≠0，
解得﹣1≤x＜2，即A={x|﹣1≤x＜2}，
由B中不等式变形得lnx＜0=ln1，得到0＜x＜1，即B={x|0＜x ＜1}，
则A∪B={x|﹣1≤x＜2}，
故选B．
2．已知，那么csα=（）
A． B． c． D．
【考点】诱导式的作用．
【分析】已知等式中的角变形后，利用诱导式化简，即可求出csα的值．
【解答】解sin（ +α）=sin（2π+ +α）=sin（ +α）=csα= ．。

河北冀州中学2017-2018学年下学期期末考试高一年级文科数学试题考试时间120分钟试题分数150分一、选择题：（共15小题。

每小题4分，共60分。

在每个小题给出的四个选项中，只有一项是符合要求的。

）1. ( )A . B. C. D.2.已知向量，满足，，则（）A． B．C． D．3.若函数，则=（）A． B． C． D．4．已知，那么（）A． B． C． D．5.已知为的边的中点，所在平面内有一个点，满足，则的值为（）A． B．C． D．6.已知是边长为1的等边三角形，则（）A． B． C． D．7．中，，则（）A. B. C. D.8.定义矩阵，若，则的图象向右平移个单位得到函数，则函数解析式为（）A. B.C. D.9.若，是第三象限角，则（）A． B． C． D．10.已知一个几何体的三视图如图所示，则该几何体的体积为（）A. B. C. D.11.的值是 ( )A． B.C. 2D.12．已知定义在R上的奇函数满足则的值为( )A. －1B.0C.1D.213．在下列四个正方体中，能得出AB⊥CD的是( )14．直线的倾斜角的取值范围是( )A．[，] B． [，C．[0，]∪（， D．[，∪[，15.若函数单调递增，则实数的取值范围是（）A. B. C. (1,3) D.(2,3)二．填空题：(共5小题，每小题4分，共20分。

)16.已知向量且A,B,C三点共线，则k= .17．已知向量、满足＝，＝，与的夹角为，则||= .18．若，且，则19.在四棱锥中，,若四边形为边长为2的正方形，,则此四棱锥外接球的表面积为 .20．圆关于直线对称，则ab的取值范围是三、解答题：（本大题共6个小题，共70分。

解答时应写出必要的文字说明、证明过程或演算步骤．）21.（本小题满分10分）已知平面向量，．（1）若，求|-|（2）若与夹角为锐角，求的取值范围．22.（本小题满分12分）已知，且，（1）求的值；（2）若，，求的值.23. (本小题满分12分)已知向量，若函数（1）求的最小正周期；(2)若，求的单调减区间24．(本小题满分12分）在锐角△ABC中，a、b、c分别为角A、B、C所对的边，且。

2017-2018学年河北省衡水市冀州中学高一（下）第一次月考语文试卷副标题一、选择题（本大题共16小题，共38.0分）1.下列加点的词解释有误．．的一项是（）A. 长余佩之陆离．．陆离：修长的样子B. 忍尤而攘．诟攘：忍受C. 苟余情其信．芳信：确实D. 又申．之以揽茝申：申述，说明【答案】D【解析】A．正确；B．正确；C．正确；D．申：加上。

译为：又因为我采集白芷而给我加上罪名；故选：D。

本题考查理解文言句子中实词含义的能力。

解答本题，要结合平时的积累以及语境进行辨析。

文言实词众多，并且一个实词有多个义项和用法，除了平常多积累之外，同学们还需掌握一些推断实词的方法，常见的文言实词推断方法有以下六种：一、字形推断法中国汉字中多为会意字和形声字，因此我们可以借助汉字的形旁来推断实词的含义。

二、邻字帮助法在文言文阅读中，实词以单音节为主，即一个字往往就是一个词。

而以两个或几个词义相同或相近的实词合起来表示一个共同的意义的现象也经常出现。

所以我们可以根据相邻的字来推断其意义。

三、成语联想法成语中保留了大量的文言词义，在解释文言实词时，我们可以联系自己熟悉的成语，加以比较验证，这对判断文言词义会有很大的帮助。

四、语法分析法所谓“语法分析法”，即运用现代汉语的语法常识，根据实词在句中的位置来确定其词性。

一般来说，在主语、宾语位置上的是名词，在谓语位置上的是动词。

受副词、数次修饰的是动词，受形容词修饰的是名词。

然后根据词性来确定词义，词性不同，词义往往不同。

五、代入验证法这是最简洁直接的方法。

把所给义项代入到句中之后，解释准确的就是正确答案。

它的局限性也在这里，就是只能适用于已给义项的题目。

六、语境分析法所谓“语境分析法”，即联系该实词在文中的前后语句甚或前后语段来推断实词意义的方法。

文言实词绝大部分是一词多义的，词义是不定项的，但我们可以结合上下文来判定实词的含义，上下文这个语境是相对稳定的，语境可以帮助我们确定词义的。