用解析法设计四杆机构共20页

按行程速比系数K设计
• 极位夹角θ和近极位传动角γ1为 • 环路AC1D投影方程
(b a) cos( 0 ) 1 c cos( 1 0 ) (b a) sin( 0 ) c sin( 1 0 )
1 2 K 1 180 K 1
• 由上式解出
2 2 2 2 ( y2 y1 )( y3 y12 x3 x12 ) ( y3 y1 )( y2 y12 x2 x12 ) x 2( x3 x1 )( y2 y1 ) ( x2 x1 )( y3 y1 ) 2 2 y2 y12 x2 x12 ( x2 x1 ) x y 2( y2 y1 ) ( y2 y1 )
按连杆给定位置设计
• 连架杆的杆长和方位角
l ( x x1 ) 2 ( y y1 ) 2
y yi i arctan xx i
按行程速比系数K设计
• 给定行程速比系数K、执行构件摆角ψ和机构远 极位传动角γ2
y C2 C1 θ A B1 a θ0 γ1 B2 d ψ D x b γ2 c
平面四杆机构设计（解析法）
1. 按连杆给定位置设计 2. 按行程速比系数置设计四杆机构
• 问题实质：求固定支座A、D的坐标值
C1 C2
b B2 B3
c
C3
B1
D a A d α4
按连杆给定位置设计
• 由某点的三个位置坐标求其转动中心坐标
( x1 x) 2 ( y1 y ) 2 ( x2 x) 2 ( y2 y ) 2 ( x1 x) 2 ( y1 y ) 2 ( x3 x) 2 ( y3 y ) 2

注意：死点、自锁与机构自由度小于等于零的区别。 自由度小于等于零，表明机构中各构件间不可作相对 运动；死点是指不计摩擦时机构所处的特殊位置，可
2021/10/10
12
借助惯性或采用机构错位排列的方法，使机构能顺 利通过死点位置而正常运转；而自锁是指机构在考 虑摩擦的情况下，当驱动力的作用方向满足一定的 几何条件时，虽然机构的自由度大于零，但机构仍 无法运动的现象。
④以O为圆心，C1O为半径作圆。
⑤作偏距线e，交圆弧于A，即为所求。
⑥以A为圆心，A C1为半径作弧交于E,得： l1 =EC2/ 2 l2 = A C2－EC2/ 2
2021/10/10
3
二、按预定连杆位置设计四杆机构
C1
a)给定连杆两组位置
C2
将铰链A、D分别 选在B1B2， C1C2连线的垂直平分线上任意 位置都能满足设计要求。
P
④作△P C1C2的外接圆，则A点必在此圆上。
⑤选定A，设Leabharlann 柄为l1 ，连杆为l2 ，则:A C1= l1+l2 ,A C2=l2- l1 => l1 =( A C1－A C2)/ 2
⑥以A为圆心，A C2为半径作弧交于E,得：
2021/1l01/1=0 EC1/ 2
l2 = A C1－EC1/ 2
7.一对心曲柄滑块机构，若以滑块为机架，则将演化
成___________机构。
8.曲柄为主动件的曲柄摇杆机构中，当从动摇杆处于
两极限位置时，________在该位置所夹的锐角，称
为极位夹角。
9.铰链四杆机构中，_____角越大，对机构的传动越
有利。
2021/10/10
22
10.死点是指不计摩擦时机构所处的特殊位置，可借 助_____或采用_____的方法使机构能顺利通过死点 位置而正常运转。

自测试题
一、 判断题（正确：T，错误：F）
1.平面连杆机构是低副机构，其接触处压强较小，因 此适用于受力较大的场合。
2.铰链四杆机构通过机架的转换，就一定可以得到曲 柄摇杆机构、双曲柄机构和双摇杆机构。
3.铰链四杆机构如有曲柄存在，则曲柄必为最短构 件。
4.在曲柄滑块机构中，当曲柄为主动件时，机构没
21
5.平行四边形机构的极位夹角=___ ,它的行程速比系 数K____。 6.铰链四杆机构演化成其它形式的四杆机构常有三种 方法，它们是______、________和_______。 7.一对心曲柄滑块机构，若以滑块为机架，则将演化 成___________机构。 8.曲柄为主动件的曲柄摇杆机构中，当从动摇杆处于 两极限位置时，________在该位置所夹的锐角，称 为极位夹角。
14
2）用作图法按两连架杆预定的对应位置 设计四杆机构 设计方法是：此类问题刚固反转法进行设计 （重点）
15
3）按预定的连杆位置设计四杆机构：
已知：连杆BC的三个预定位置B1C1、B2C2和B3C3 设计的实质是：求固定铰链中心的位置 设计方法是：此类问题可用求圆心法来解决，即作 铰链B各位置点连线B1B2 、B2B3的中垂线，两中 垂线的交点即为固定铰链中心A。同理，作铰链C 各位置点连线C1C2、 C2C3的中垂线，两中垂线的 交点即为固定铰链中心D。
9.铰链四杆机构中，_____角越大，对机构的传动越 有利。
22
10.死点是指不计摩擦时机构所处的特殊位置，可借 助_____或采用_____的方法使机构能顺利通过死点 位置而正常运转。
三、选择题
1.下面
不是平面连杆机构的优点。
A. 运动副是面接触，故压强小、耐磨损；

三 对 对 应 位 置 （ ． ） （ ， ） （ ， ） 则 有 下 列 、 、 也 ，
关 系 ：
Ｃ８ ： Ｏ ＋ ｏ （ ） Ｐ ０ 咖】 Ｓ ｃ ｓ 妇一 ＋ ２ ｃ ｓ＞－ ０ Ｐｌ ８ 如一她） Ｐ ｏ ４Ｆ ８ ｃ （ ０ ＋ ２ Ｃ ８ ｏ ｃ ｓ 只ｃ ｓ 如一 ） Ｏ 也ｔ ｏ ＋ ｏ （ ＋ Ｐ，
ａｌ 、 ／ 、 ｃ 根 据 实 际 需 要 决 定 构 件 的 长 度 ｃ 其 ｃ ｂ ｃ ｄ， 再 ， 余 构 件 的 长 度 。 ６、 便 可 最 后 确 定 。 、 ｄ 然 而 ， 生 产 实 践 中 ， 常 要 求 原 动 件 和 从 动 在 常
件 之 间 能 实 现 三对 以 上 或 更 多 的 对 应 位 置 关 系 。根
在 生 产 实 践 中 ， 常 要 求 平 面 四 杆 机 构 的 原 动 常 件 和 从 动 件 之 间 能 实 现 三 对 以 上 或 更 多 对 对 应 的 位 置 关 系 。 解 析 法 只 能 准 确 实 现 原 动 件 和 从 动 件 之
间 的 三 对 对 应 位 置 关 系 ，实 验 法 虽 然 能 近 似 地 解 决
其 中 、 、 同前 。 只
（ ４）
显 然 ． 要 知 道 原 动 件 和 从 动 件 的 四对 对 应 位 其 置 关 系 ， 可 以 求 出 ： 、 ／ 、 ／ 和 ０ 然 后 ． 据 实 就 ６ ｃａ ｄａ 。 根
际 需 要 确 定 构 件 ＡＢ的 长 度 口 从 而 即 可 确 定 机 构 其 ，
若 以 构 件 Ｃ 的 长 度 ｃ 基 准 ， 按 方 程 （ ） （ ） Ｄ 为 １ 、２ 、 （ ） 确 定 ， ３可 ， ，进 而 求 解 出其 余 的 相 对 长 度

设计
已知活动铰点B、C中心位置，求固定铰链A、D 中心位置。
B1
C1
B2
A●
●D
C2
四杆机构 AB1C1D 为所求.
第29页/共41页
实现连杆给定的三个位置
C1 C2
B1 B2
B3 C3
D
A
四杆机构 AB1C1D 为所求.
第30页/共41页
2.具有急回特性的机构
第31页/共41页
按给定的 K 值,设计曲柄摇杆机构
4 D
lCD
3 D
e
B
1
2
C3
A 4
对心式曲柄滑块机构
B
2
C3
e0 1
A 4
偏置式曲柄滑块机构
第11页/共41页
e ——偏心距 e =0 为曲柄滑块机构 e≠0 为偏置曲柄滑块
运动特点： 曲柄的回转运动变换为滑块的往复直线运动（如空压机）
或将滑块的往复直线运动变换为回转运动（如内燃机）。
第12页/共41页
• 传动角为零=0(连杆与从动件共线),机构顶死
C
C
C2
2
1
3
B
B
vF
B1 =00
1
A
B2
4
=00
A
B2
D
=00
B
=00
C１
C
C
1
F
2
v
第22页/共41页
克服死点的措施
• 利用构件惯性力
• 实例:家用缝纫机
• 采用多套机构错位排列
• 实例:蒸汽机车车轮联动机构
• 蒸汽机车两侧利用错位排列的两套曲柄滑块机构使车
1） 给定 K、y、LCD

按照相对运动关系，可画出该机构 的运动简图。如图4-21b所示。由图可 知，偏心轮是回转副B扩大到包括回转 副A而形成的，偏心距e即曲柄的长度。
6．双滑块机构 曲柄滑块机构演化为具有两个移动 副的四杆机构，称为双滑块机构。 在图4-22a所示的曲柄滑块机构中， 将转动副B扩大，则图a所示的曲柄滑块 机构，可等效为图b所示的机构。
利用错列机构克服平行四边形 机构不确定性状态
利用辅助曲柄消除平行四边形机构 的不确定状态
三、双摇杆机构
两连架杆均为摇杆的铰链四杆机构 称为双摇杆机构。 图4-11所示为起重机机构，当摇杆 CD摇动时，连杆BC上悬挂重物的M点 作近似的水平直线移动，从而避免了重 物平移时因不必要的升降而发生的事故 和能量的损耗。
2．导杆机构 图4-16a）所示为 曲柄滑块机构。
若取曲柄为机架， 则为演变为导杆机构， 如图4-16b）所示。
若AB<BC，则杆2和杆4均可作整周回转， 故称为转动导杆机构。若AB>BC，则杆4 均只能作往复摆动，故称为摆动导杆机构。
图4-17牛头刨床的摆动导杆机构
又如图4-18为牛头刨床回转导杆机 构，当BC杆绕B点作等速转动时，AD 杆绕A点作变速转动DE杆驱动刨刀作变 速往返运动。
§4-2 铰链四杆机构的演化
一、铰链四杆机构的曲柄存在条件 铰链四杆机构中是否存在曲柄，取 决于机构各杆的相对长度和机架的选择。 如图4-13所示的机构中，杆1为曲柄，杆 2为连杆，杆3 为摇杆，杆4为机架，各杆 长度以l1、l2、l3、l4表示。为了保证曲柄 1 整周回转，曲柄 1 必须能顺利通过与机 架4共线的两个位置AB’和AB’’。
曲柄摇杆机构 双曲柄机构
双摇杆机构
一、 曲柄摇杆机构

以A为圆心、 l1为半径作圆， 交C1A的延长线于
B1， 交C2A于B2， 即可得连杆的长度l2=B1C1=B2C2
以及机架的长度l4=AD。 机构AB1C1D即为该机构在
极限位置时的运动简图。
返回
机械设计基础
cos l2 cos l4 l3 cos
sin l2 sin l3 sin
机械设计基础
Machine Design Foundation
平面四杆机构的设计
该机构的四个杆组成封闭多边形。取各杆在坐标轴 x和y上的投影，可得以下关系式：
将cosφ和sinφ平移到等式右边，再把等式两边平
机械设计基础
Machine Design Foundation
平面四杆机构的设计
1.3 按给定的行程速度变化系数设计
在设计具有急回特性的平面四杆机构时， 通常 按照实际的工作需要， 先确定行程速度变化系数K的
数值， 并按式（6 - 2）计算出极位夹角θ， 然后利用
机构在极限位置时几何关系， 再结合其它有关的附加 条件进行四杆机构的设计， 从而求出机构中各个构件 的尺寸参数。
P
平面四杆机构的设计
NM
图6- 25 按K值设计曲柄摇杆机构
机械设计基础
Machine Design Foundation
平面四杆机构的设计
解 设计的实质就是确定曲柄与机架组成的固定
铰链中心A的位置， 并求出机构中其余三个构件的长 度l1、 l2和l4。
其设计步骤如下：
(1) 计算极位夹角θ。
根据给定的行程速度变化系数K， 由式（4 - 9）计
解 设计的实质就是确定连架杆与机架组成的固定
铰链中心A和D的位置， 并由此求出机构中其余三个构 件的长度l1、 l3和l4。

四杆机构第三章平⾯四杆机构的设计§3—1 平⾯连杆机构的特点、类型及应⽤1.1 概述连杆机构：各构件之间⽤低副和刚性构件连接起来实⾏运动传递的机构。

如图2-1 分为平⾯连杆机构和空间连杆机构。

连杆机构由连架杆，连杆和机架组成。

平⾯连杆机构的特点：1.2平⾯连杆机构的基本类型和结构特点：由于连杆机构的构件⼀般呈杆状，也以其构件的数量称为多杆机构。

平⾯杆机构是最基本最常⽤的连杆机构。

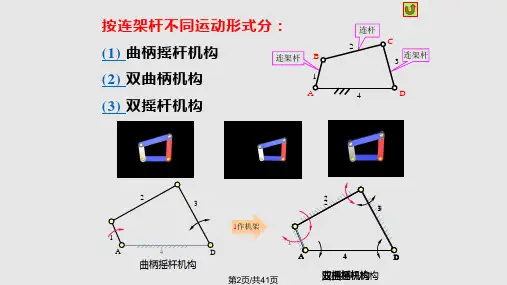
1．2．1 平⾯连杆机构的基本类型：1) 曲柄摇杆机构 2）双曲柄机构 3）双摇杆机构 1．2．2 平⾯连杆机构演化 1) 转动副转化为移动副 2）取不同的构件为机架3）变换构件的形态 4）扩⼤转动副的尺⼨§3—2 平⾯连杆机构的运动特性2.1平⾯连杆机构的运动特性：（1的Grashoff 定理（简称曲柄存在条件）a + d ≤b + cb ≤ d – a +c c ≤d – a + b a ≤ c a + b ≤ c + da ≤b a +c ≤ b +d a ≤ d a + d ≤ b + c在全铰链四杆机构中，如果最短杆与最长杆杆长之和⼩于或等于其余两杆杆长之和，则必然存在作整周转动的构件。

若不满⾜上述条件，即最短杆与最长杆杆长之和⼤于其余两杆杆长之和，则不存在作整周转动的构件。

（2）四杆机构从动件的急回特性：如图⽰四杆机构从动件的回程所⽤时间⼩于⼯作⾏程所⽤的时间，称为该机构急回特性。

急回特性⽤⾏程速⽐系数K 表⽰。

212112??===t t v v K极位夹⾓θ—— 从动摇杆位于两极限位置时，原动件两位置所夹锐⾓。

θ越⼤，K 越⼤，急回特性越明显。

§3—3 平⾯连杆机构的传⼒特性3．1．传动⾓与压⼒⾓：如图⽰在机构处于某⼀定位置时，从动件上作⽤⼒与作⽤点绝对速度⽅向所夹的锐⾓α称为压⼒⾓。

压⼒⾓的余⾓γ（γ = 90°— α）作为机构的传⼒特性参数，故称为传动⾓。

在四杆机构运动过程中，压⼒⾓和传动⾓是变化的，为使机构具有良好的传⼒特性应使压⼒⾓越⼩越好，传动⾓越⼤越好。

第37页/共87页
§4-2 铰链四杆机构的演化
一、铰链四杆机构的曲柄存在条件 铰链四杆机构中是否存在曲柄，取决于机构各杆的相对长度和机架的选
择。如图4-13所示的机构中，杆1为曲柄，杆2为连杆，杆3 为摇杆，杆4为机架， 各杆长度以l1、l2、l3、l4表示。为了保证曲柄1整周回转，曲柄1必须能顺利通过与 机架4共线的两个位置AB’和AB’’。
第51页/共87页
2．导杆机构 图4-16a）所示为曲柄滑块机构。
若取曲柄为机架，则为演变为导 杆机构，如图4-16b）所示。
若AB<BC，则杆2和杆4均可作整周回转，故称为转动导杆机构。若AB>BC，则杆4 均只能作往复摆动，故称为摆动导杆机构。
第52页/共87页
图4-17牛头刨床的摆动导杆机构
曲柄摇杆机构
双曲柄机构 双摇杆机构
第5页/共87页
一、 曲柄摇杆机构
在铰链四杆机构中，若两个连架杆，一个为曲柄，另一个为摇杆，则 此铰链四杆机构称为曲柄摇杆机构。
图4-2所示为调整雷达天线俯仰角的曲柄摇杆机构。曲柄1缓慢地匀速转 动，通过连杆2使摇杆3在一定的角度范围内摇动，从而调整天线俯仰角的大小。
第19页/共87页
在实际应用中，为度量方便起见，
常用压力角的余角来衡量机构传力性 能的好坏，称为传力角。显然值越大 越好，理想情况是=90。
一般机械中，=40~50。
大功率机构，min=50。
非传动机构，<40，但不能过小。
第20页/共87页
确 定 最 小 传 动 角 min 。 由 图 4-5 中
第25页/共87页
图4-6 利用死点夹紧工件的夹具
第26页/共87页
二、双曲柄机构 两连架杆均为曲柄的铰链四杆机构称为双曲柄机构。

代入解析方程式， 列 方程组求解未知参数
（4）插值结点的选取 在结点处应有
f(x)-F(x)=0
偏差大小取决结点数目 和分布位置
结点以外的其他位置的偏差为 y f ( x ) F ( x ) 0 结点数：最多为5个
结点位置的分布根据函数逼近理论按下式选取：
xi ( xm x0 )/2 - ( xm x0 )cos[180(2i 1)/(2 m)] / 2
( x x D ) 2 ( y yD )2 g 2 f 2 2[ g ( x x D ) f ( y yD )] cos 2 2[ f ( x x D ) g ( y yD )] sin 2 c 2
( x x A )2 ( y yA )2 e 2 f 2 2[e ( x x A ) f ( y yA )] cos 2 2[ f ( x x A ) e ( y yA )] sin 2 a 2
P0 n P1 ( n / l ) P ( l 2 n2 1 m 2 ) /( 2l ) 3
n= 1.533 l =1.442 m=1.783
根据结构要求，确定曲柄长
度，可求各构件实际长度。
（2）按预期函数设计四杆机构 ★期望函数：要求四杆机 构两连架杆转角之间实现 的函数关系 y=f(x)。
3、按预定的运动轨迹设计四杆机构
左侧杆组 设计要求：确定机构的各尺度 参数和连杆上的描点位置M， 使该点所描绘的连杆曲线与预 右侧杆组 定的轨迹相符。 设计思路：分别按左侧杆组 和右侧杆组的矢量封闭图形 写出方程解析式。
联 立 求 解
( x x A )2 ( y yA )2 e 2 f 2 2[e ( x x A ) f ( y yA )] cos 2 2[ f ( x x A ) e ( y yA )] sin 2 a 2

两极限位置间的夹角称为摇杆的摆角。
图4-4 曲柄摇杆机构的急回特性
当曲柄由AB1顺时针转到AB2时，
曲柄转角1=180+，这时摇杆由C1D摆 到C2D，摆角为；而当曲柄顺时针再转 过角度2=180-时，摇杆由C2D摆回C1D， 其摆角仍然是 。虽然摇杆来回摆动的
摆角相同，但对应的曲柄转角不等
(12);当曲柄匀速转动时,对应的时间
图4-19自卸卡车翻斗机构及其运动简图
4．定块机构
图4-16a）所示 曲柄滑块机构。
若取杆3为固定件， 即可得图4-16d）所示 的固定滑块机构或称 定块机构。
这种机构常用于 如图4-20所示抽水唧筒 机构中。
图4-20所示为抽水唧筒机构及其运动简图
5．偏心轮机构
图4-21a所示为偏心轮机构。杆1为 圆盘，其几何中心为B。因运动时该圆 盘绕偏心A转动，故称偏心轮。 A、B之 间的距离e称为偏心距。
的锐角称为压力角。由图可见，力P在vc 方向的有效分力为Pt=Pcos，
图4-5 压力角与传动角
它可使从动件产生有效的回转力矩， 显然Pt越大越好。而P在垂直于vc方向的
分力Pn=Psin则为无效分力，它不仅无
助于从动件的转动，反而增加了从动件 转动时的摩擦阻力矩。因此，希望Pn越
小越好。由此可知，压力角越小，机 构的传力性能越好，理想情况是=0，
由上述分析可知：
最短杆和最长杆长度之和小于或等于其 余两杆长度之和是铰链四杆机构存在曲 柄的必要条件。
满足这个条件的机构究竟有一个曲柄、 两个曲柄或没有曲柄，还需根据取何杆 为机架来判断。
二、铰链四杆机构的演化
1．曲柄滑块机构
如图4-15a所示 的曲柄摇杆机构中， 摇杆3上C点的轨迹是以D为圆心，杆3的 长度L3为半径的圆弧mm。如将转动副D 扩大，使其半径等于L3，并在机架上按C 点的近似轨迹mm作成一弧形槽，摇杆3 作成与弧形槽相配的弧形块，如图4-14b 所示。

3.4 图解法设计平面四杆机构3.4.1按连杆位置设计四杆机构1.给定连杆的三个位置给定连杆的三个位置设计四杆机构时，往往是已知连杆B C的长度L B C和连杆的三个位置B1C1和B2C2和B3C3时，怎样设计四杆机构呐？图解过程。

：：1：：：：2：：2.给定连杆的两个位置给定连杆的两个位置B1C1和B2C2时与给定连杆的三个位置相似，设计四杆机构图解过程如下。

①选定长度比例尺绘出连杆的两个位置B1C1、B2C2。

②连接B1B2、C1C2，分别作线段B1B2和C1C2的垂直平分线B12和C12，分别在B12和C12上任意取A，D两点，A，D两点即是两个连架杆的固定铰链中心。

连接A B1、C1D、B1C1、A D，A B1C1D即为所求的四杆机构。

③测量A B1、C1D、A D计算l A B、L C D L A D的长度,由于A点可任意选取，所以有无穷解。

在实际设计中可根据其他辅助条件，例如限制最小传动角或者A、D的安装位置来确定铰链A、D的安装位置。

例设计一振实造型机的反转机构，要求反转台8位于位置Ⅰ（实线位置）时，在砂箱7内填砂造型振实，反转台8反转至位置Ⅱ（虚线线位置）时起模，已知连杆B C长0.5m和两个位置B1C1、B2C2.。

要求固定铰链中心A、D在同一水平线上并且A D=B C。

自己可以试着在纸上按比例作出图形，再求出各杆长度。

若想对答案请点击例题祥解3.4.2 按行程速度变化系数设计四杆机构1.设计曲柄摇杆机构按行程速度变化系数K设计曲柄摇杆机构往往是已知曲柄机构摇杆L3的长度及摇杆摆角ψ和速度变化系数K。

怎样用作图法设计曲柄摇杆机构？2.设计曲柄摆动导杆机构已知机架长度l4和速度变化系数K，设计曲柄导杆机构。

①求出极位夹角②根据导杆摆角ψ等于曲柄极位夹角θ，任选一点C后可找出导杆两极限C m、C n。

③作∠M C N的角评分线，取C A＝，得到A点，过A点作C m和C n的垂线B1和B2两点，A B1（或A B2）即为曲柄。

实现预定轨迹的例题
鹤式起重机
搅拌机
连杆
1．平面四杆机构中，是否存在死点取决于
是否与
连杆共线。
A 、主动件 B、 从动件 C、 机架 D、 摇杆
2、在设计铰链四杆机构时，应使最小传动角 。 A、 尽可能小一些 B 、为0 C、 尽可能大一些 D、 为90
3.一对心曲柄滑块机构中，如果将曲柄改为机架，则将演 化为 机构。
4．下面简图所示的铰链四杆机构，图 是双曲柄机构。 A）a； B）b； C）c； D）d。
(a)
(b)
(c)
(d)
二、平面连杆机构设计
图解法 解析法 实验法
（一）图解法
简单、直观、 易理解知识点、误差大。
1.给定连杆的位置要求设计四杆机构
（1）给定连杆的两个位置设计四杆机构
已知连杆长度，连杆的2个（或3，4。。 个）工作位置B1C1与B2C2。设计此四杆机构。
一 、四杆机构设计的基本问题
1）实现给定位置的设计（导引机构设计） 2）实现预定运动规律的设计（函数机构设计） 3）实现预定轨迹的设计（轨迹机构设计）
1.实现给定位置的设计
例如：满足预定的连杆位置要求
要求所设计的机构 能引导连杆顺序通 过一系列给定的位 置。即要求连杆能 依次占据一系列给 定的位置。
（3）极为夹角=0，则K=1，无急回 运动；
（4）角越大，则K值越大，说明急回 运动的性质也越显著。
曲柄滑块机构中，原动件AB以 1 等速转动
B
a1
2
C2
b
C3 C1
1
A B1 H
4
B2
偏置曲柄滑块机构
H (a b )2 e2(b a )2 e2

二、急回特性
急回特性 机构工作件返回行程速度大于工作行程速度的特性。 行程速比系数K 为了表示工作件往复运动时的急回程度，用V2和V1的比值K来描述。
急回性能分析
V2 c2c1 / t 2 t1 1 1800 k V1 c1c2 / t1 t 2 2 1800
演化：曲柄摇杆机构
回转副D→移动副 曲柄滑块机构
§2.2 平面四杆机构的基本形式及其演化
类型：
曲柄滑块机构（偏距e） 对心曲柄滑块机构， e=0 滑块运动线与曲柄回转中心共线 偏置曲柄滑块机构，e≠0 滑块运动线与曲柄回转中心不共线 特点：曲柄等速回转，滑块具有急 回特性。
应用：活塞式内燃机，空气压缩
§2.2 平面四杆机构的基本形式及其演化
曲柄摇杆机构应用实例
缝纫机脚踏板机构
§2.2 平面四杆机构的基本形式及其演化
曲柄摇杆机构应用实例
跑步机
§2.2 平面四杆机构的基本形式及其演化
曲柄摇杆机构应用实例
自动送料机构
§2.2 平面四杆机构的基本形式及其演化
2.双曲柄机构——两连杆架均为曲柄的四杆机构 连杆架 曲柄—原动件，等速转动 曲柄—从动件，变速转动
l1+l4≤ l2+ l3 将式2-1、2-2、2-3两两相加，可得 l1≤l2 ， l1≤l3 ， l1≤l4 AB杆（曲柄）为最短杆 最短杆与任意一杆长度之和≤其它两杆长度之和
§2.3 平面四杆机构的几个基本概念
铰链四杆机构有一个曲柄的条件： (1) 最短杆与最长杆之和小于或等于其余两杆长度之和；
Fn
1 1
A
B
2

4

3 D
g C a
F

这两个条件必须同时满足，否则机构中不存在 整转副，无论取哪个构件作机架都只能得到双摇 杆机构。
18
另外，具有整转副的铰链四杆机构是否存 在曲柄，还应根据选择何杆为机架来判断。 (1) 取最短杆为机架时，机架上有两个整转副， 故得双曲柄机构。
19
(2) 取最短杆的邻边为机架时，机架上只有一 个整转副，故得曲柄摇杆机构。
共线。此时杆１与杆２的夹角β的变化范围为也是 0o ～360 0
杆３为摇杆，它与相邻两杆的夹角ψ 、γ 的 变化范围小于360°。
显然，Ａ、Ｂ为整转副， Ｃ、Ｄ不是整转副。
为了实现曲柄 １整周回转，AB杆 必须顺利通过与连 杆共线的两个位置 AB′和AB″。
15
当杆１处于AB′位置时，形成三角形 ACD 。
摇杆自C2D摆回至C1D是其空回行程，这时 Ｃ点的平均速度是v2=C1C2 ／t2，显然v1 < v2 ， 它表明摇杆具有急 回运动的特性。牛 头刨床、往复式输 送机等机械就利用 这种急回特性来缩 短非生产时间，提 高生产率。
4
急回运动特性可用行程速度变化系数（也称 行程速比系数）K 表示。
v2
பைடு நூலகம்
C1C2/t2
根据三角形任意两边之和必大于(极限情况下等于)
第三边的定理可得
l4≤(l2 －l1)＋l3
l3≤(l2 －l1)＋l4
即 l1＋l4≤l2＋l3 （2-4） l1＋l3≤l2＋l4 （2-5）
当杆１处于AB″位置
时，形成三角形ACD 。
可得
l1 ＋ l2 ≤l4 ＋ l3
（2-6）
16
将式(2-4)、(2-5)、(2-6)两两相加
l1＋l4≤l2＋l3
（2-4）

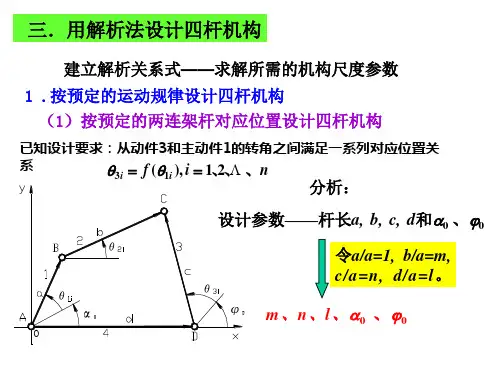
5.5平面四杆机构的解析法设计5.5.1按许用传动角设计曲柄摇杆机构设已知从动摇杆的摆角ψ、行程速比系数K，机架的杆长d＝1，许用传动角[γ]，设曲柄的杆长a为参变量，用解析法[23]确定连杆的杆长b以及摇杆的杆长c。

由行程速比系数K求出极位夹角θ，即θ＝180(K－1)/(K＋1)。

在图5.20中，由△B1B0B2得B1B2＝2c sin(0.5ψ)，对△A0B1B2应用余弦定理得由此得a、b、c 与θ的函数关系对△A3B3B0应用余弦定理得将式(5.13)代入式(5.14)，得以 a 为设计变量的设计方程为设已知从动摇杆的摆角ψ、若θ＝0，K＝1，机架的杆长d＝1，许用传动角[γ]。

用解析法确定曲柄的杆长a、连杆的杆长b以及摇杆的杆长c。

在图5.21中，K＝1，摇杆在B3B0、B4B0位置出现最小传动角且两个最小传动角相等，对△A1B1B0、△A1B2B0应用余弦定理化简上式得机构杆长之间的约束方程为对△A4B4B0、△A3B3B0应用余弦定理得化简上式得令式(5.13)中的θ＝0，得杆长c的函数式为联立式(5.20)～(5.23)得曲柄的杆长a、连杆的杆长 b 以及摇杆的杆长 c 的设计方程为【点击链接曲柄摇杆机构的设计动画】5.5.2刚体导引机构的解析法设计刚体导引机构是指它的连杆能够通过一系列有限分离位置的一种机构。

其解析法设计就是建立机构的结构参数与运动参数之间的关系式，采用适宜的数学方法，按一定的精度要求，求出机构的未知参数。

1)平面位移矩阵设一连杆在平面坐标系xOy 中占据n 个位置，连杆的第j(j＝1,2,…，n)个位置用向量P j Q j表示。

如图5.22 所示，连杆由位置P1Q1运动到P j Q j可以看成由P1Q1平移到P j Q'j再绕Pj 点转动θ1j的运动之和。

设[Rθ1j]表示连杆旋转θ1j后，其上的向量在旋转前后的关系矩阵，则( Qj －Pj ) = [Rθ1j]( Q'j－P j ) 由于Qj －Pj = Q1 －P1为此( Qj －Pj ) = [Rθ1j]( Q1 －P1 )式中［D1j］为[D1j]称为平面位置矩阵。