Fisher判别-jing

fisher判别准则
Fisher判别准则是一种分类算法，主要用于将多维数据分为两
个类别。

该算法的核心是通过最大化类别间距离和最小化类别内部距离来确定决策边界，从而实现对新数据的分类。

具体来说，该算法首先计算每个类别的均值向量和协方差矩阵，然后通过类别间距离和类别内部距离的比值来确定最佳的决策边界。

决策边界可以用一个线性方程表示，因此该算法也称为线性判别分析（LDA）。

由于Fisher判别准则考虑了类别间的差异和类别内部的相似性，因此在处理高维数据时表现出色。

同时，该算法还可以用于特征选择和降维，有助于简化数据处理过程。

总之，Fisher判别准则是一种有效的分类算法，可用于处理多
维数据和进行特征选择。

在实际应用中，可以根据具体问题的性质选择适合的分类算法并进行实验验证。

- 1 -。

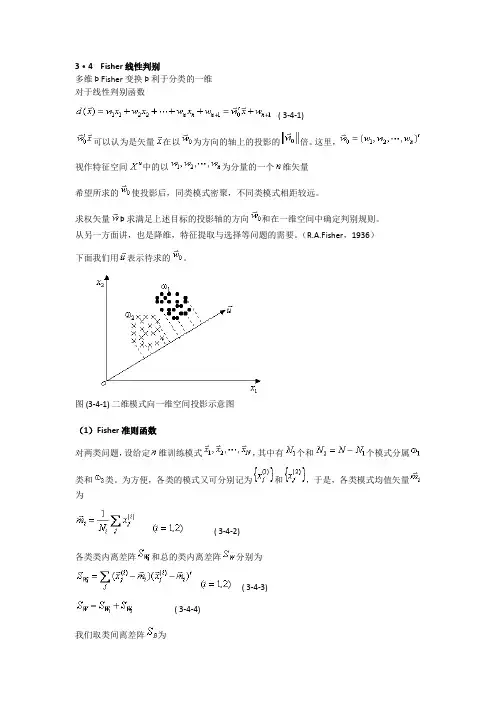
3·4 Fisher线性判别多维 Þ Fisher变换 Þ 利于分类的一维对于线性判别函数( 3-4-1)可以认为是矢量在以为方向的轴上的投影的倍。

这里，视作特征空间中的以为分量的一个维矢量希望所求的使投影后，同类模式密聚，不同类模式相距较远。

求权矢量Þ 求满足上述目标的投影轴的方向和在一维空间中确定判别规则。

从另一方面讲，也是降维，特征提取与选择等问题的需要。

（R.A.Fisher，1936）下面我们用表示待求的。

图 (3-4-1) 二维模式向一维空间投影示意图（1）Fisher准则函数对两类问题，设给定维训练模式，其中有个和个模式分属类和类。

为方便，各类的模式又可分别记为和，于是，各类模式均值矢量为( 3-4-2)各类类内离差阵和总的类内离差阵分别为( 3-4-3)( 3-4-4)我们取类间离差阵为( 3-4-5)作变换，维矢量在以矢量为方向的轴上进行投影( 3-4-6)变换后在一维空间中各类模式的均值为( 3-4-7)类内离差度和总的类内离差度为( 3-4-8)( 3-4-9)类间离差度为( 3-4-10)我们希望经投影后，类内离差度越小越好，类间离差度越大越好，根据这个目标作准则函数( 3-4-11)称之为Fisher准则函数。

我们的目标是，求使最大。

（2）Fisher变换将标量对矢量微分并令其为零矢量，注意到的分子、分母均为标量，利用二次型关于矢量微分的公式可得( 3-4-12)令可得当时，通常是非奇异的，于是有( 3-4-13)上式表明是矩阵相应于本征值的本征矢量。

对于两类问题，的秩为1，因此只有一个非零本征值，它所对应的本征矢量称为Fisher最佳鉴别矢量。

由式( 3-4-13)有( 3-4-14)上式右边后两项因子的乘积为一标量，令其为，于是可得式中为一标量因子。

这个标量因子不改变轴的方向，可以取为1,于是有( 3-4-15)此时的是使Fisher准则函数取最大值时的解，即是维空间到一维空间投影轴的最佳方向，( 3-4-16)称为Fisher变换函数。

关于fisher判别的⼀点理解最近⼀个朋友问这⽅⾯的⼀些问题，其实之前也就很粗略的看了下fisher，真正帮别⼈解答问题的时候才知道原来⾃⼰也有很多东西不懂。

下⾯⼩结下⾃⼰对fisher判别的理解：其实fisher和PCA差不多，熟悉PCA的⼈都知道，PCA其实就是在寻找⼀个⼦空间。

这个空间怎么来的呢，先求协⽅差矩阵，然后求这个协⽅差矩阵的特征空间（特征向量对应的空间），选取最⼤的特征值对应的特征向量组成特征⼦空间（⽐如说k个，相当于这个⼦空间有k 维，每⼀维代表⼀个特征，这k个特征基本上可以涵盖90%以上的信息）。

那么我们把样本投影在这个⼦空间，原来那么多维的信息就可以⽤这k维的信息代替了，也就是说降维了。

⾄于PCA为啥要⽤求协⽅差矩阵然后求特征⼦空间的⽅法，这个数学上有证明，记得在某篇⽂章上看过，有兴趣的可以找找，看看证明。

那么fisher空间⼜是怎么⼀回事呢，其实fisher判别和PCA是在做类似的⼀件事，都是在找⼦空间。

不同的是,PCA是找⼀个低维的⼦空间，样本投影在这个空间基本不丢失信息。

⽽fisher是寻找这样的⼀个空间，样本投影在这个空间上，类内距离最⼩，类间距离最⼤。

那么怎么求这个空间呢，类似于PCA，求最⼤特征值对应的特征向量组成的空间。

当我们取最⼤⼏个特征值对应的特征向量组成特征空间时（这⾥指出，最佳投影轴的个数d<=c-1，这⾥c是类别数），最佳投影矩阵如下：其实在⽂章Eigenfaces vs Fisherfaces ：recognition using class specific linear projection中给出了PCA和LDA⽐较直观的解释，⽂中对⼀个⼆维的数据进⾏分析,PCA和LDA都是把⼆维数据降到⼀个⼀维空间，那么其实PCA使得数据投影在这个⼀维空间总的离散度最⼤，我的理解是这样的，如果数据在某⼀维上⽐较离散，说明这维特征对数据的影响⽐较⼤，也就是说这维特征是主成分。

Fisher判别函数，也称为线性判别函数（Linear Discriminant Function），是一种经典的模式识别方法。

它通过将样本投影到一维或低维空间，将不同类别的样本尽可能地区分开来。

一、算法原理：Fisher判别函数基于以下两个假设：1.假设每个类别的样本都服从高斯分布；2.假设不同类别的样本具有相同的协方差矩阵。

Fisher判别函数的目标是找到一个投影方向，使得同一类别的样本在该方向上的投影尽可能紧密，而不同类别的样本在该方向上的投影尽可能分开。

算法步骤如下：(1)计算类内散度矩阵（Within-class Scatter Matrix）Sw，表示每个类别内样本之间的差异。

Sw = Σi=1 to N (Xi - Mi)(Xi - Mi)ᵀ，其中Xi 表示属于类别i 的样本集合，Mi 表示类别i 的样本均值。

(2)计算类间散度矩阵（Between-class Scatter Matrix）Sb，表示不同类别之间样本之间的差异。

Sb = Σi=1 to C Ni(Mi - M)(Mi - M)ᵀ，其中 C 表示类别总数，Ni 表示类别i 中的样本数量，M 表示所有样本的均值。

(3)计算总散度矩阵（Total Scatter Matrix）St，表示所有样本之间的差异。

St =Σi=1 to N (Xi - M)(Xi - M)ᵀ(4)计算投影方向向量w，使得投影后的样本能够最大程度地分开不同类别。

w= arg max(w) (wᵀSb w) / (wᵀSw w)，其中w 表示投影方向向量。

(5)根据选择的投影方向向量w，对样本进行投影。

y = wᵀx，其中y 表示投影后的样本，x 表示原始样本。

(6)通过设置一个阈值或使用其他分类算法（如感知机、支持向量机等），将投影后的样本进行分类。

二、优点和局限性：Fisher判别函数具有以下优点：•考虑了类别内和类别间的差异，能够在低维空间中有效地区分不同类别的样本。

论文(设计)《模式识别》题目Fisher线性判别的基本原理及应用Fisher判别准则一、基本原理思想Fisher线性判别分析的基本思想：通过寻找一个投影方向（线性变换，线性组合），将高维问题降低到一维问题来解决，并且要求变换后的一维数据具有如下性质：同类样本尽可能聚集在一起，不同类的样本尽可能地远。

Fisher线性判别分析，就是通过给定的训练数据，确定投影方向W和阈值y0，即确定线性判别函数，然后根据这个线性判别函数，对测试数据进行测试，得到测试数据的类别。

二、算法的实现及流程图1 算法实现 （1）W 的确定x 1m x, 1,2ii X ii N ∈==∑各类样本均值向量mi样本类内离散度矩阵和总类内离散度矩阵Tx S (x m )(x m ), 1,2ii i i X i ∈=--=∑样本类间离散度矩阵T1212S (m m )(m m )b =--在投影后的一维空间中，各类样本均值。

样本类内离散度和总类内离散度。

样本类间离散度。

Fisher 准则函数满足两个性质：·投影后，各类样本内部尽可能密集，即总类内离散度越小越好。

·投影后，各类样本尽可能离得远，即样本类间离散度越大越好。

根据这个性质确定准则函数，根据使准则函数取得最大值，可求出W ：。

（2）阈值的确定采取的方法：【1】【2】【3】（3）Fisher 线性判别的决策规则对于某一个未知类别的样本向量x ，如果y=W T·x>y0，则x ∈w1；否则x ∈w2。

2 流程图归一化处理载入训练数据三、实验仿真1.实验要求试验中采用如下的数据样本集:ω1类： (22,5),(46,33),(25,30),(25,8),(31, 3),(37,9),(46,7),(49,5),(51,6),(53,3)(19,15),(23,18),(43,1),(22,15),(20,19),(37,36),(22,22),(21,32),(26,36),(23,39)(29,35),(33,32),(25,38),(41,35),(33,2),(48,37)ω2类: (40,25),(63,33),(43,27),(52,25),(55,27),(59,22) ,(65,59),(63,27)(65,30),(66,38),(67,43),(52,52),(61,49) (46,23),(60,50),(68,55) (40,53),(60,55),(55,55) (48,56),(45,57),(38,57) ,(68,24)在实验中采用Fisher线性判别方法设计出每段线性判别函数。

1实验1 Fisher 线性判别实验一、实验目的应用统计方法解决模式识别问题的困难之一是维数问题，在低维空间行得通的方法，在高维空间往往行不通。

因此，降低维数就成为解决实际问题的关键。

Fisher 的方法，实际上涉及维数压缩。

如果要把模式样本在高维的特征向量空间里投影到一条直线上，实际上就是把特征空间压缩到一维，这在数学上容易办到。

问题的关键是投影之后原来线性可分的样本可能变得混杂在一起而无法区分。

在一般情况下，总可以找到某个最好的方向，使样本投影到这个方向的直线上是最容易分得开的。

如何找到最好的直线方向，如何实现向最好方向投影的变换，是Fisher 法要解决的基本问题。

这个投影变换就是我们寻求的解向量*w本实验通过编制程序体会Fisher 线性判别的基本思路，理解线性判别的基本思想，掌握Fisher 线性判别问题的实质。

二、实验原理1．线性投影与Fisher 准则函数各类在d 维特征空间里的样本均值向量：∑∈=ik X x kii xn M 1，2,1=i (4.5-2)通过变换w 映射到一维特征空间后，各类的平均值为：∑∈=ik Y y kii yn m 1，2,1=i (4.5-3)映射后，各类样本“类内离散度”定义为：22()k ii k i y Y S y m ∈=-∑，2,1=i (4.5-4)显然，我们希望在映射之后，两类的平均值之间的距离越大越好，而各类的样本类内离散度越小越好。

因此，定义Fisher 准则函数：2122212||()F m m J w s s -=+ (4.5-5) 使F J 最大的解*w 就是最佳解向量，也就是Fisher 的线性判别式。

2．求解*w从)(w J F 的表达式可知，它并非w 的显函数，必须进一步变换。

2已知：∑∈=ik Y y ki i yn m 1，2,1=i , 依次代入(4.5-1)和(4.5-2)，有：i TX x kiT k X x T ii M wx n w x w n m ik ik ===∑∑∈∈)1(1，2,1=i (4.5-6)所以：221221221||)(||||||||M M w M w M w m m TTT-=-=-w S w w M M M M w b T T T =--=))((2121 (4.5-7) 其中：T b M M M M S ))((2121--= (4.5-8)b S 是原d 维特征空间里的样本类内离散度矩阵，表示两类均值向量之间的离散度大小，因此，b S 越大越容易区分。

实验1 Fｉsｈｅr线性判别实验一、实验目的应用统计方法解决模式识别问题的困难之一是维数问题，低维特征空间的分类问题一般比高维空间的分类问题简单。

因此，人们力图将特征空间进行降维，降维的一个基本思路是将ｄ维特征空间投影到一条直线上,形成一维空间，这在数学上比较容易实现。

问题的关键是投影之后原来线性可分的样本可能变为线性不可分。

一般对于线性可分的样本,总能找到一个投影方向，使得降维后样本仍然线性可分。

如何确定投影方向使得降维以后，样本不但线性可分,而且可分性更好（即不同类别的样本之间的距离尽可能远，同一类别的样本尽可能集中分布)，就是Fisher线性判别所要解决的问题。

本实验通过编制程序让初学者能够体会Fｉsｈer线性判别的基本思路，理解线性判别的基本思想，掌握Ｆｉsheｒ线性判别问题的实质。

二、实验要求1、改写例程，编制用Fishｅr线性判别方法对三维数据求最优方向W的通用函数。

2、对下面表1-１样本数据中的类别ω1和ω２计算最优方向W。

3、画出最优方向W的直线，并标记出投影后的点在直线上的位置。

表1-1 Fｉｓｈｅr线性判别实验数据４、选择决策边界,实现新样本xx1＝（-0.7,０.５8，0.0８9),xｘ2＝(0．047,-０．４,1.０4)的分类。

５、提高部分（可做可不做)：设某新类别ω3数据如表１-2所示,用自己的函数求新类别ω3分别和ω1、ω２分类的投影方向和分类阈值。

表1-２新类别样本数据三、部分参考例程及其说明求取数据分类的Fiｓher投影方向的程序如下：其中w为投影方向。

clear %Removeｓａll vａriａbleｓfrｏm thｅworksｐaｃe.cｌc %Clｅａrs the ｃommanｄwinｄoｗ anｄｈomｅs thｅ cuｒsor．% ｗ1类训练样本，10组，每组为行向量。

w1=[－０.４,０.5８,0.０89;-0.31,0.27,-0．０4;-0．３8,0．05５,-0.035;－0.１５,0．5３,0.011;-0．３５，0．47,0.0３4；.．.0．１7，０.6９,0．１；-0.０11,0.５5，-０.18;－0.27，0.61,0.12;－０.065,0．４9，0.０012;-0．12,0.054,-0.063];% w2类训练样本，１0组，每组为行向量。

1 绪 论1.1课题背景随着社会经济不断发展，科学技术的不断进步，人们已经进入了信息时代，要在大量的信息中获得有科学价值的结果，从而统计方法越来越成为人们必不可少的工具和手段。

多元统计分析是近年来发展迅速的统计分析方法之一，应用于自然科学和社会各个领域，成为探索多元世界强有力的工具。

判别分析是统计分析中的典型代表，判别分析的主要目的是识别一个个体所属类别的情况下有着广泛的应用。

潜在的应用包括预测一个公司是否成功；决定一个学生是否录取；在医疗诊断中，根据病人的多种检查指标判断此病人是否有某种疾病等等。

它是在已知观测对象的分类结果和若干表明观测对象特征的变量值的情况下，建立一定的判别准则，使得利用判别准则对新的观测对象的类别进行判断时，出错的概率很小。

而Fisher 判别方法是多元统计分析中判别分析方法的常用方法之一，能在各领域得到应用。

通常用来判别某观测量是属于哪种类型。

在方法的具体实现上，采用国内广泛使用的统计软件SPSS（Statistical Product and Service Solutions ）,它也是美国SPSS 公司在20世纪80年代初开发的国际上最流行的视窗统计软件包之一 1.2 Fisher 判别法的概述根据判别标准不同，可以分为距离判别、Fisher 判别、Bayes 判别法等。

Fisher 判别法是判别分析中的一种，其思想是投影，Fisher 判别的基本思路就是投影，针对P 维空间中的某点x=(x1，x2，x3，…，xp)寻找一个能使它降为一维数值的线性函数y(x)： ()j j x C x ∑=y然后应用这个线性函数把P 维空间中的已知类别总体以及求知类别归属的样本都变换为一维数据，再根据其间的亲疏程度把未知归属的样本点判定其归属。

这个线性函数应该能够在把P 维空间中的所有点转化为一维数值之后，既能最大限度地缩小同类中各个样本点之间的差异，又能最大限度地扩大不同类别中各个样本点之间的差异，这样才可能获得较高的判别效率。

Fisher判别法课程设计一、课程目标知识目标：1. 理解Fisher判别法的原理和数学推导过程；2. 学会运用Fisher判别法解决实际问题，如对给定的数据集进行判别分析；3. 掌握Fisher判别法在统计学习中的应用范围和限制。

技能目标：1. 能够运用所学软件（如R、Python等）实现Fisher判别法的计算过程；2. 能够通过实际案例，运用Fisher判别法对数据进行预处理和特征提取；3. 能够分析判别结果，对模型的性能进行评估和优化。

情感态度价值观目标：1. 培养学生独立思考、团队协作的能力，激发学生学习统计学习的兴趣；2. 培养学生面对实际问题，敢于尝试、勇于探索的精神；3. 增强学生对我国在统计学习领域取得的成果的认识，提高国家自豪感。

课程性质：本课程为高年级统计学或相关专业的专业课程，旨在让学生掌握Fisher判别法这一经典统计学习方法。

学生特点：学生已具备一定的数学基础和统计学知识，具有一定的编程能力。

教学要求：通过本课程的学习，使学生能够将Fisher判别法应用于实际问题，并具备独立解决实际问题的能力。

教学过程中注重理论与实践相结合，培养学生的实际操作能力和创新精神。

教学评估将以学生在实际案例中的应用表现为主，注重学生的过程学习和能力提升。

二、教学内容1. 引入Fisher判别法的背景和基本概念，介绍Fisher线性判别和Fisher二次判别的原理；- 教材章节：第三章“判别分析”，第一节“Fisher判别法”；- 内容安排：讲解Fisher判别法的数学推导，分析线性与二次判别的区别及适用场景。

2. 讲解Fisher判别法的计算步骤和实际应用案例；- 教材章节：第三章“判别分析”，第二节“Fisher判别法的计算与应用”；- 内容安排：通过实际案例，演示Fisher判别法的计算过程，分析判别效果。

3. 学习使用统计软件（如R、Python）实现Fisher判别法；- 教材章节：第三章“判别分析”，第三节“Fisher判别法的软件实现”；- 内容安排：教授学生如何利用统计软件进行Fisher判别法的计算，掌握相关函数和操作。