Fisher判别

Fisher判别法课程设计一、教学目标本节课的教学目标是使学生掌握Fisher判别法的基本原理和应用方法。

知识目标包括：了解Fisher判别法的数学背景和原理，掌握Fisher判别函数的推导过程，理解Fisher判别法的应用场景。

技能目标包括：能够运用Fisher判别法解决实际问题，能够使用相关软件进行Fisher判别法的计算和分析。

情感态度价值观目标包括：培养学生的数据分析能力和科学思维，激发学生对统计学的兴趣和热情。

二、教学内容本节课的教学内容主要包括Fisher判别法的原理和应用。

首先，介绍Fisher判别法的基本概念和数学背景，解释判别函数的推导过程。

然后，通过实例分析，展示Fisher判别法在实际问题中的应用，如分类问题和判别分析。

最后，结合教材和课外资料，进行深入学习，探讨Fisher判别法的优缺点和适用条件。

三、教学方法为了达到本节课的教学目标，将采用多种教学方法相结合的方式进行教学。

首先，采用讲授法，系统地讲解Fisher判别法的原理和推导过程。

其次，通过案例分析法，引导学生运用Fisher判别法解决实际问题，培养学生的应用能力。

此外，还采用讨论法，鼓励学生积极参与课堂讨论，提出问题和观点，培养学生的思考能力和团队合作精神。

最后，利用实验法，让学生亲自动手进行实验，验证Fisher判别法的有效性，提高学生的实践能力。

四、教学资源为了支持本节课的教学内容和教学方法的实施，将准备以下教学资源。

首先，教材和相关参考书籍，为学生提供系统的学习材料。

其次，多媒体资料，如PPT和教学视频，用于辅助讲解和展示Fisher判别法的原理和应用。

此外，实验设备，如计算机和统计软件，用于学生进行实验和实践操作。

最后，网络资源，如学术期刊和在线课程，为学生提供更多的学习参考和拓展资料。

五、教学评估本节课的教学评估将采用多元化的评估方式，以全面、客观地评价学生的学习成果。

评估方式包括平时表现、作业和考试。

Fisher 判别函数的使用具体步骤Fisher 多类判别模型假定事物由p 个变量描述, 即: x=(p x x x ,...,,21)T该种事物有G 个类型, 从每个类型中顺次抽取p n n n ,...,,21个样品, 共计n=∑=Gi i1n个样品。

即从第g 类取了g n 个样品, g=1,2,⋯, G, 第g 类的第i 个样品, 用向量:gi x =(pgi gi gi x x ,...,,x 21)T (1)( 1) 式中, 第一个下标是变量号, 第二个下标是类型号,第三个下标是样品号。

设判别函数为:T x p p v x v x v x v =+++=...y 2211 （2）其中: V=(p v v v ,...,21)T按照组内差异最小, 组间差异最大同时兼顾的原则, 来确定判别函数系数。

（中间推导过程不在这里介绍了）最终就有个判别函数:,y x V Tj j=1,...,2,1s j = 一般只取前M=min(G- 1,p)个, 即:M j x v x v x v y p pj j j j ,...,2,1,...2211=+++= （3）根据上述M 个判别函数, 可对每一个待判样品做出判别。

),...,,(x 020100p x x ｘ=其过程如下:1、把x0 代入式(3) 中每一个判别函数, 得到M 个数,,...,2,1,...y 202101j 0M j x v x v x v p pj j j =+++=记：TM y y y y ),...,,(020100= 2、把每一类的均值代入式（3）得Gg y y y y G g M j x v x v x v y M gggg pg pg g g g g j g ,...,2,1),,...,,(,...2,1,,...,2,1,...212211====+++=3、计算：∑=-=Mj j j g gy y D 1202)(，从这G 个值中选出最小值：)(min 212g Gg h D D ≤≤=。

Fisher判别是一种基于线性判别分析的分类方法，用于将样本分为不同的类别。

其基本步骤如下：
1. 确定判别变量：首先需要确定用于判别的变量，即用于分类的特征。

2. 计算判别函数：根据样本数据，计算出判别函数，即用于将样本分为不同类别的函数。

3. 确定判别类别：根据判别函数，将样本分为不同的类别。

4. 计算判别准确率：计算分类准确率，即正确分类的样本数与总样本数之比。

5. 优化判别函数：根据判别准确率，调整判别函数，以提高分类准确率。

6. 重复步骤3~5：重复以上步骤，直到达到所需的分类准确率。

在Fisher判别中，判别函数是基于Fisher线性判别的，即对于每个类别，计算出一个线性函数，使得属于该类别的样本与属于其他类别的样本的距离最大化。

这个过程可以通过矩阵运算和求导来实现。

总之，Fisher判别是一种基于线性判别分析的分类方法，其基本步骤包括确定判别变量、计算判别函数、确定判别类别、计算判别准确率、优化判别函数和重复步骤3~5，直到达到所需的分类准确率。

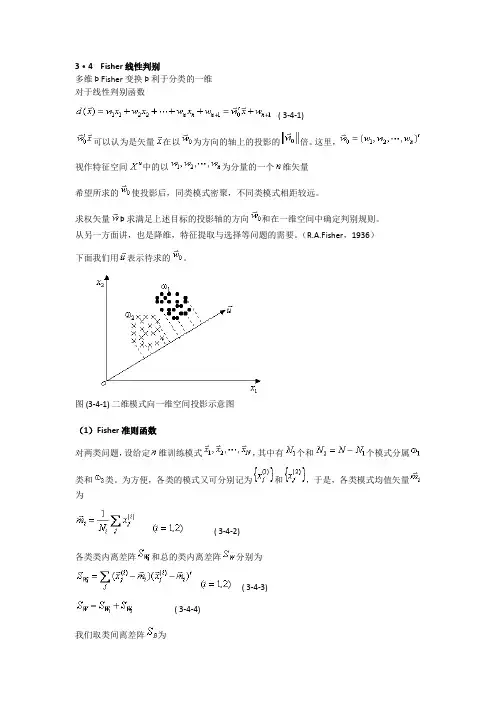
3·4 Fisher线性判别多维 Þ Fisher变换 Þ 利于分类的一维对于线性判别函数( 3-4-1)可以认为是矢量在以为方向的轴上的投影的倍。

这里，视作特征空间中的以为分量的一个维矢量希望所求的使投影后，同类模式密聚，不同类模式相距较远。

求权矢量Þ 求满足上述目标的投影轴的方向和在一维空间中确定判别规则。

从另一方面讲，也是降维，特征提取与选择等问题的需要。

（R.A.Fisher，1936）下面我们用表示待求的。

图 (3-4-1) 二维模式向一维空间投影示意图（1）Fisher准则函数对两类问题，设给定维训练模式，其中有个和个模式分属类和类。

为方便，各类的模式又可分别记为和，于是，各类模式均值矢量为( 3-4-2)各类类内离差阵和总的类内离差阵分别为( 3-4-3)( 3-4-4)我们取类间离差阵为( 3-4-5)作变换，维矢量在以矢量为方向的轴上进行投影( 3-4-6)变换后在一维空间中各类模式的均值为( 3-4-7)类内离差度和总的类内离差度为( 3-4-8)( 3-4-9)类间离差度为( 3-4-10)我们希望经投影后，类内离差度越小越好，类间离差度越大越好，根据这个目标作准则函数( 3-4-11)称之为Fisher准则函数。

我们的目标是，求使最大。

（2）Fisher变换将标量对矢量微分并令其为零矢量，注意到的分子、分母均为标量，利用二次型关于矢量微分的公式可得( 3-4-12)令可得当时，通常是非奇异的，于是有( 3-4-13)上式表明是矩阵相应于本征值的本征矢量。

对于两类问题，的秩为1，因此只有一个非零本征值，它所对应的本征矢量称为Fisher最佳鉴别矢量。

由式( 3-4-13)有( 3-4-14)上式右边后两项因子的乘积为一标量，令其为，于是可得式中为一标量因子。

这个标量因子不改变轴的方向，可以取为1,于是有( 3-4-15)此时的是使Fisher准则函数取最大值时的解，即是维空间到一维空间投影轴的最佳方向，( 3-4-16)称为Fisher变换函数。

Fisher判别函数，也称为线性判别函数（Linear Discriminant Function），是一种经典的模式识别方法。

它通过将样本投影到一维或低维空间，将不同类别的样本尽可能地区分开来。

一、算法原理：Fisher判别函数基于以下两个假设：1.假设每个类别的样本都服从高斯分布；2.假设不同类别的样本具有相同的协方差矩阵。

Fisher判别函数的目标是找到一个投影方向，使得同一类别的样本在该方向上的投影尽可能紧密，而不同类别的样本在该方向上的投影尽可能分开。

算法步骤如下：(1)计算类内散度矩阵（Within-class Scatter Matrix）Sw，表示每个类别内样本之间的差异。

Sw = Σi=1 to N (Xi - Mi)(Xi - Mi)ᵀ，其中Xi 表示属于类别i 的样本集合，Mi 表示类别i 的样本均值。

(2)计算类间散度矩阵（Between-class Scatter Matrix）Sb，表示不同类别之间样本之间的差异。

Sb = Σi=1 to C Ni(Mi - M)(Mi - M)ᵀ，其中 C 表示类别总数，Ni 表示类别i 中的样本数量，M 表示所有样本的均值。

(3)计算总散度矩阵（Total Scatter Matrix）St，表示所有样本之间的差异。

St =Σi=1 to N (Xi - M)(Xi - M)ᵀ(4)计算投影方向向量w，使得投影后的样本能够最大程度地分开不同类别。

w= arg max(w) (wᵀSb w) / (wᵀSw w)，其中w 表示投影方向向量。

(5)根据选择的投影方向向量w，对样本进行投影。

y = wᵀx，其中y 表示投影后的样本，x 表示原始样本。

(6)通过设置一个阈值或使用其他分类算法（如感知机、支持向量机等），将投影后的样本进行分类。

二、优点和局限性：Fisher判别函数具有以下优点：•考虑了类别内和类别间的差异，能够在低维空间中有效地区分不同类别的样本。

论文(设计)《模式识别》题目Fisher线性判别的基本原理及应用Fisher判别准则一、基本原理思想Fisher线性判别分析的基本思想：通过寻找一个投影方向（线性变换，线性组合），将高维问题降低到一维问题来解决，并且要求变换后的一维数据具有如下性质：同类样本尽可能聚集在一起，不同类的样本尽可能地远。

Fisher线性判别分析，就是通过给定的训练数据，确定投影方向W和阈值y0，即确定线性判别函数，然后根据这个线性判别函数，对测试数据进行测试，得到测试数据的类别。

二、算法的实现及流程图1 算法实现 （1）W 的确定x 1m x, 1,2ii X ii N ∈==∑各类样本均值向量mi样本类内离散度矩阵和总类内离散度矩阵Tx S (x m )(x m ), 1,2ii i i X i ∈=--=∑样本类间离散度矩阵T1212S (m m )(m m )b =--在投影后的一维空间中，各类样本均值。

样本类内离散度和总类内离散度。

样本类间离散度。

Fisher 准则函数满足两个性质：·投影后，各类样本内部尽可能密集，即总类内离散度越小越好。

·投影后，各类样本尽可能离得远，即样本类间离散度越大越好。

根据这个性质确定准则函数，根据使准则函数取得最大值，可求出W ：。

（2）阈值的确定采取的方法：【1】【2】【3】（3）Fisher 线性判别的决策规则对于某一个未知类别的样本向量x ，如果y=W T·x>y0，则x ∈w1；否则x ∈w2。

2 流程图归一化处理载入训练数据三、实验仿真1.实验要求试验中采用如下的数据样本集:ω1类： (22,5),(46,33),(25,30),(25,8),(31, 3),(37,9),(46,7),(49,5),(51,6),(53,3)(19,15),(23,18),(43,1),(22,15),(20,19),(37,36),(22,22),(21,32),(26,36),(23,39)(29,35),(33,32),(25,38),(41,35),(33,2),(48,37)ω2类: (40,25),(63,33),(43,27),(52,25),(55,27),(59,22) ,(65,59),(63,27)(65,30),(66,38),(67,43),(52,52),(61,49) (46,23),(60,50),(68,55) (40,53),(60,55),(55,55) (48,56),(45,57),(38,57) ,(68,24)在实验中采用Fisher线性判别方法设计出每段线性判别函数。

实验1 Fisher线性判别实验一、实验目的应用统计方法解决模式识别问题的困难之一是维数问题，低维特征空间的分类问题一般比高维空间的分类问题简单。

因此，人们力图将特征空间进行降维，降维的一个基本思路是将d维特征空间投影到一条直线上，形成一维空间，这在数学上比较容易实现。

问题的关键是投影之后原来线性可分的样本可能变为线性不可分。

一般对于线性可分的样本，总能找到一个投影方向，使得降维后样本仍然线性可分。

如何确定投影方向使得降维以后，样本不但线性可分，而且可分性更好（即不同类别的样本之间的距离尽可能远，同一类别的样本尽可能集中分布），就是Fisher线性判别所要解决的问题。

本实验通过编制程序让初学者能够体会Fisher线性判别的基本思路，理解线性判别的基本思想，掌握Fisher线性判别问题的实质。

二、实验要求1、改写例程，编制用Fisher线性判别方法对三维数据求最优方向W的通用函数。

2、对下面表1-1样本数据中的类别ω1和ω2计算最优方向W。

3、画出最优方向W的直线，并标记出投影后的点在直线上的位置。

表1-1 Fisher线性判别实验数据4、选择决策边界，实现新样本xx1=（-0.7,0.58,0.089），xx2=（0.047,-0.4,1.04）的分类。

5、提高部分（可做可不做）：设某新类别ω3数据如表1-2所示，用自己的函数求新类别ω3分别和ω1、ω2分类的投影方向和分类阈值。

表1-2 新类别样本数据三、部分参考例程及其说明求取数据分类的Fisher投影方向的程序如下：其中w为投影方向。

clear %Removes all variables from the workspace.clc %Clears the command window and homes the cursor.% w1类训练样本，10组，每组为行向量。

w1=[-0.4,0.58,0.089;-0.31,0.27,-0.04;-0.38,0.055,-0.035;-0.15,0.53,0. 011;-0.35,0.47,0.034;...0.17,0.69,0.1;-0.011,0.55,-0.18;-0.27,0.61,0.12;-0.065,0.49,0.0012;-0 .12,0.054,-0.063];% w2类训练样本，10组，每组为行向量。

Fisher判别理论，编程步骤和优缺点1.理论判别分析是用于判别个体所属群体的一种统计方法，判别分析的特点是根据已掌握的、历史上每个类别的若干样本的数据信息，总结出客观事物分类的规律性，建立判别公式和判别准则。

然后，当遇到新的样本点时，只要根据总结出来的判别公式和判别准则，就能判别该样本点所属的类别。

判别分析是一种应用性很强的统计数据分析方法。

Fisher判别（1）借助方差分析的思想构造一个线性判别函数：（2）确定判别函数系数时要求使得总体之间区别最大，而使每个总体内部的离差最小。

（3）从几何的角度看，判别函数就是p维向量X在某种方向上的投影。

使得变换后的数据同类别的点“尽可能聚在一起”，不同类别的点“尽可能分离”，以此达到分类的目的。

两类Fisher判别示意图（1）如果有多个类别， Fisher 判别可能需要两个或者更多的判别函数才能完成分类。

（2）一般来说判别函数的个数等于分类的个数减一。

（3）得到判别函数后，计算待判样品的判别函数值，根据判别函数的值计算待判样品到各类的重心的距离，从而完成分类。

2.编程步骤① 把来自两类21/w w 的训练样本集X 分成1w 和2w 两个子集1X 和2X 。

G1 G2X② 由∑∈=i k X x k ii x n M 1，2,1=i ，计算i M 。

③ 由T i X x k i k i M x M x S ik ))((--=∑=计算各类的类内离散度矩阵i S ，2,1=i 。

④ 计算类内总离散度矩阵21S S S w +=。

⑤ 计算w S 的逆矩阵1-w S 。

⑥ 由)(211*M M S w w -=-求解*w 。

3.优点（1）一般对于线性可分的样本，总能找到一个投影方向，使得降维后的样本仍然线性可分，而且可分性更好即不同类别的样本之间的距离竟可能的远，同一类别的尽可能的集中分布。

（2）Fisher 方法可以直接求解法向量。

（3）Fisher 的线性判别不仅适用于确定性的模式分类器的训练，而且对于随机的模机也是适用的，Fisher 还可以推广到多类问题中去。

Fisher线性判别分析
Fisher线性判别分析
1、概述
在使⽤统计⽅法处理模式识别问题时，往往是在低维空间展开研究，然⽽实际中数据往往是⾼维的，基于统计的⽅法往往很难求解，因此降维成了解决问题的突破⼝。

假设数据存在于d维空间中，在数学上，通过投影使数据映射到⼀条直线上，即维度从d维变为1维，这是容易实现的，但是即使数据在d维空间按集群形式紧凑分布，在某些1维空间上也会难以区分，为了使得数据在1维空间也变得容易区分，需要找到适当的直线⽅向，使数据映射在该直线上，各类样本集群交互较少。

如何找到这条直线，或者说如何找到该直线⽅向，这是Fisher线性判别需要解决的问题。

2、从d维空间变换到1维空间
3、介绍⼏个基本的参量
A. 在d维原始空间
B. 在1维映射空间
4、Fisher准则函数
5、学习算法推导
6、决策分类。