角的度量与比较

角的度量与比较角是平面几何中的基本概念之一，它是由两条射线共同起点组成的图形。

在数学和几何学中，了解角的度量和比较是非常重要的。

本文将探讨角的度量方法以及如何进行角的比较。

一、角的度量方法角的度量单位通常是度（°），角度可以通过度数来表示。

一圆周的度数为360°。

角度用于测量角的大小，也可以用于测量旋转的程度。

有以下几种方法来度量角的大小。

1. 度数制：以圆周的度数为单位来度量角的大小。

当角所对的弧长等于圆的半径时，这个角的度数为1°。

通过测量角所对的弧长可以计算出角的大小。

2. 弧度制：弧度是度数制的补充，它是一种无单位的角度度量方法。

弧度的定义是，当一个角所对的弧长等于半径时，这个角的弧度为1。

弧度制在解决圆周运动问题时非常有用，通常用于微积分和物理学中。

3. 百分度数制：除了度数制和弧度制之外，还可以使用百分度数制来度量角的大小。

一圆周被分为100个等分，每个等分被称为一个百分度（%），因此一个右角的大小为90%。

二、角的比较方法角度的大小可以用来比较角的大小。

在比较角的大小时，常常需要考虑以下几点：1. 角的度数：通过比较角的度数，可以确定哪个角比较大，哪个角比较小。

例如，一个角的度数为45°，另一个角的度数为60°，可以得出第二个角比第一个角更大。

2. 角的弧度：使用弧度制来度量角时，可以通过比较角所对的弧长来确定角的大小。

弧长越大，角度就越大。

3. 角的位置：角的位置也可以决定角的大小。

当两个角位于同一条直线的同一侧时，可以比较它们与直线的夹角。

夹角较大的角更大。

如果两个角位于同一条直线的相对侧面，那么这两个角的和将等于180°，我们可以通过比较它们与直线的夹角来确定它们的相对大小。

4. 角的比较符号：在进行角的比较时，可以使用角的比较符号来表示比较的结果。

常见的角的比较符号有“>”（大于）、“<”（小于）和“=”（等于）。

角的度量与比较角是在数学中常见的概念，用来描述物体或图形之间的相对方向关系。

在几何学中，角可以通过度量和比较来描述其大小和关系。

本文将对角的度量和比较进行介绍和解释。

一、角的度量角的度量通常用角度来表示，常见的单位有度（°）和弧度（rad）。

度是指一个平面角所占据的空间角的1/360部分，而弧度则是角所对应的弧所占据的弧长与半径的比值。

换句话说，一个完整的圆周对应的弧度是2π。

根据这个关系，我们可以将角的度量进行转换。

举个例子来说明，如果一个角所对应的弧长是半径的一半，我们就可以称之为一个直角。

根据圆周对应的弧度是2π，我们可以计算得知直角所对应的弧度是π/2。

因此，直角的度量可以用90°或π/2 rad来表示。

在实际应用中，我们常常使用度来度量角，因为它更容易理解和计算。

而弧度则在更高级的数学和物理学中使用较多，因为它和三角函数的关系更为简洁。

二、角的比较在几何学中，我们经常需要进行角的比较。

这可以通过比较角度的大小或比较角的关系来实现。

1. 比较角度大小比较角度大小是通过确定两个角度的差异来进行的。

如果两个角度的差值是正数，则表示第一个角度较大；如果差值是负数，则表示第一个角度较小。

例如，如果一个角度是30°，另一个角度是60°，那么它们的差值是60°-30°=30°，说明第一个角度较小。

2. 比较角的关系比较角的关系主要包括三种情况：相等、锐角和钝角。

当两个角的度量相等时，我们可以称它们为相等角。

相等角意味着两个角所对应的弧长相等或角度相等。

当一个角的度量小于90°时，我们称之为锐角。

锐角表示两个物体或者图形之间的相对方向是接近的。

当一个角的度量大于90°时，我们称之为钝角。

钝角表示两个物体或者图形之间的相对方向是偏离的。

三、角的应用角的概念在日常生活和实际应用中非常重要。

它被广泛应用于测量、导航、工程设计和图形图像处理等领域。

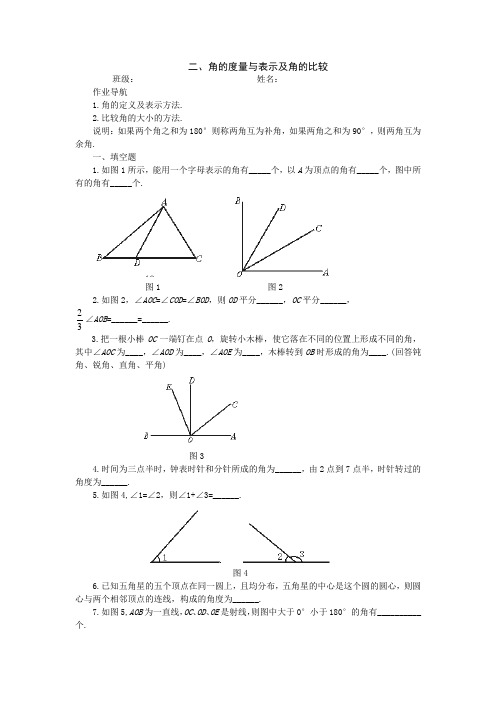
二、角的度量与表示及角的比较班级：___________________________姓名：___________________________ 作业导航1.角的定义及表示方法.2.比较角的大小的方法.说明：如果两个角之和为180°则称两角互为补角，如果两角之和为90°，则两角互为余角.一、填空题1.如图1所示，能用一个字母表示的角有_____个，以A 为顶点的角有_____个，图中所有的角有_____个.图1 图22.如图2，∠AOC =∠COD =∠BOD ，则OD 平分______，OC 平分______，32∠AOB =______=______. 3.把一根小棒OC 一端钉在点O ，旋转小木棒，使它落在不同的位置上形成不同的角，其中∠AOC 为____，∠AOD 为____，∠AOE 为____，木棒转到OB 时形成的角为____.(回答钝角、锐角、直角、平角)图34.时间为三点半时，钟表时针和分针所成的角为______，由2点到7点半，时针转过的角度为______.5.如图4,∠1=∠2，则∠1+∠3=______.图46.已知五角星的五个顶点在同一圆上，且均分布，五角星的中心是这个圆的圆心，则圆心与两个相邻顶点的连线，构成的角度为______.7.如图5,AOB 为一直线，OC 、OD 、OE 是射线，则图中大于0°小于180°的角有__________个.图58.如果一个角的度数为n ，则它的补角为______，余角为______.9.∠α的补角为125°，∠β的余角为37°，则α、β的大小关系为α__________β. 二、选择题10.一个角等于它的补角的5倍，那么这个角的补角的余角是（ ） ° ° ° ° 11.两个锐角的和（ ）A.一定是锐角B.一定是钝角C.一定是直角D.以上三种情况都有可能 12.互为补角的两个角度比是3∶2，这两个角是（ ） °,72° °，85° °，80° °，70° 13.下列各角中是钝角的为（ ）A.41周角 B.65平角 C.32直角D.31直角 14.如果角α和角β互为余角,角α与角γ互为补角,角β和角γ的和等于周角的31，那么此三个角分别为（ ）°,15°,105° °,30°, 120° °, 30°,130° °, 20°, 110° 15.如图6，图形表示的是（ ）A.直线B.射线C.平角D.周角图616.船的航向从正北按顺时针方向转到东南方向，它转了（ ） ° ° ° °17.有两个角，它们的比为7∶3，它们的差为72°，则这两个角的关系是（ ） A.互为余角 B.互为补角C.相等D.以上答案都不对 三、解答题18.四个角的和是180°，其中有三个角相等，且都是第四个角的32，求这四个角. 19.如图7，已知∠AOC =∠BOD =75°，∠BOC =30°，求∠AO D.图7 图820.如图8，已知O是直线AB上的点，OD是∠AOC的平分线，OE是∠COB的平分线，求∠DOE的度数.二、角的度量与表示及角的比较一、1. 2 3 72.∠BOC∠AOD∠AOD∠BOC3.锐角直角钝角平角° 165°°°°－n 90°－n 9.＞二、三、°，40°，40°，60°°°。

角的度量与表示，大小比较教学目标:1、 通过丰富的实例，进一步理解角的有关概念，认识角的表示2、 认识度、分、秒，会进行简单的换算3、 在现实情境中，进一步丰富对角与锐角、钝角、直角、平角、周角及其大小关系的认识4、 会比较角的大小，能估计一个角的大小5、 在操作活动中认识角的平分线，能画出一个角的平分线教学重点：理解角的概念，用字母表示角；比较角的大小，能估计一个角的大小 教学难点：1进行简单的度、分、秒的换算 2正确认识角的平分线 知识点：一、 用字母表示角图1C 图2C图3角的表示：角用符号“∠”表示，常见有以方法：（1） 用三个大写英文字母表示：如图1，可记作∠AOB 或∠BOA ，其中O 是角的顶点，必须写中间，A 、B 分别是角的两边上的一点，写在两边，可以交换位置（2） 用一个大写英文字母表示：如图1，可记作∠O 。

用这种方法表示的前提是同一个点作顶点的角只有一个时，否则不能用这种表示方法。

如图2，∠AOC 就不能记作∠O ，因为此时以O 为顶点的角不止一个，容易引起混淆。

（3） 用数字或希腊字母来表示，用这种方法表示角时，要在靠近顶点处加上弧线，注上阿拉伯数字或小写希腊字母α、β、γ等，如图2中，∠AOB 可记作∠1，∠BOC 记作∠2，如图3中，∠AOB 记作∠β，∠BOC 记作∠α二、度、分、秒的换算从量角器上看到，把一个平角180等分，每一份就是1度的角，为了更精密地度量角，把1°的60等分，每份叫做1分的度，记作1′，又把1′的度60等分，每一份叫做1秒的角，记作1″。

即1°=60′；1′=60″ 三、角的比较：角是可以比较的，由比较的结果，可分为两角相等、不相等且有大小之分.（1）重合法：CC（F ） （F ）A B B CA B （D ）（D ）（E ）（D ）（F ） （图1）（图2）（图3）（E ）移动∠DEF 使顶点E 与顶点B 重合，一边ED 和BA 重合，另一边EF 和BC 落在BA 的同旁若EF 和BC 重合，记作∠DEF ＝∠ABC 如上图1 若EF 落在∠ABC 的外部，记作∠DEF>∠ABC 如上图2 若EF 落在∠ABC 的内部，记作∠DEF<∠ABC 如上图3结论：比较两角∠ABC 与∠DEF 的大小的结果有且只有下列三种情况之一：∠DEF ＝∠ABC ，∠DEF>∠ABC ，∠DEF<∠ABC.（2）度量法：在小学学过用量角器量一个角.方法:①分别量出两个角的度数.②比较两个度数的大小. 结果:度数大的角大.注意：角的大小与两边画的长短无关. 四、角的和、差、倍、分 （1）两角的和:完成如下变化:把∠2移到∠1上, 使顶点重合,一边重合, ∠2在∠1外部,所形成的∠ABC 是∠1与∠2的和.表示: ∠ABC=∠1+∠2 （如图）（2）两角的差:当∠2在∠1的内部时,它们的另一边所成的角(∠DEF)是它们的差. （如图） 表示:∠DEF=∠1－∠2（3）角的倍分图形：意义：如果两个∠1的和是∠ABC ，那么∠ABC 是∠1的2倍. （如图）表示：∠ABC ＝2∠1 （4）角的几分之一： 意义：若∠ABC ＝2∠1则∠1是∠ABC 的二分之一. 表示:∠1=21∠ABC. （如图） 五、角的平分线:（1）定义:从一个角的顶点,引出一条射线把这个角分成两个相等的角,这条射线叫做这个角的平分线.（2）图形:（3）表示方法:∠AOB=2∠AOC=2∠BOC或: ∠AOC=∠BOC=21∠AOBBAC OAC2 1B121 1ABC112D21FE 1B11C课堂练习 一、填空题1.45°=_____直角=______平角=_____周角.2.∠α+∠β=90°,且∠α=2∠β,则∠α=___________，∠β=_________.3.0.5°=_______′=_______″; 1800″=_______°=_______′.4.(601)°=_______′=_______″, 32.81°=_______°_______′_______″. 57.32°=___度_____分____秒. 27°14′24″=__度.5.时钟的时针三小时旋转的角度是_______，分针三分钟旋转的角度是_______.6.如图，锐角的个数共有_______个. 二、判断题 1.∠1是钝角，则21∠1一定是锐角. （ ） 2.图中∠CAB 也可表 示成∠A .（ ）3.两条射线组成的图形叫做角. （ ）4.两条直线相交形成的图形叫做角.（ ）5.射线绕它上面一点旋转形成的图形叫做（ ）三、∠AOB 的度数与时钟4：00整时时针与分针所成的角度相同，那么∠AOB =___°，21∠AOB =_ °,90°－31∠AOB =90°－__°=_ _°. 四、解答题1.两角差是36°，且它们的度数比是3∶2，则这两角的和是多少？ 解法一：设这两角度数分别为(3x )°和(2x )°，则根据题意列方程为：解方程：__________________________, x =____________,∴3x +2x =______________.解法二：设这两个角的度数和为x °，则这两个角分别为_______和_______，根据题意列方程为：_______________________________解方程_____________________________ ∴这两角的和是____________°.2.请将图中的角用不同方法表示出来，并填写下表：∠ABE∠1 ∠2 ∠33.小亮利用星期天搞社会调查活动，早晨8：00出发，中午12：30到家，问小亮出发时和到家时时针和分针的夹角各为多少度.4.如图，用字母A、B、C表示∠α、∠β.5．三角板如下图所示放置，在图上加弧线的角为多少度？6. 请估计下面角的大小，然后再用量角器测量.课后练习一、填空题1.由_______的_______射线组成的图形叫做角.2.一条以一个角的_______为_______的射线把这个角分成_______的角，这条射线叫做这个角的_______.3.一副三角板的六个角各是_______、_______、_______、_______、_______、_______.4.一个周角是一个平角的_________倍，一个平角是一个直角的_________倍.5.根据右图，比较∠AOC、∠BOD、∠BOC、∠COD、∠AOD的大小，它们从小到大排列为___________.二、判断题1.一条线就是一个平角.（）2.从一个角的顶点出发，把它分成两个角的直线叫做这个角的平分线.（）3.一个角的两边越长，这个角就越大.（）三、读图填空1.如下左图，∠BDC=_______+_______，∠CDA=_______－_______.2.如上右图，OC⊥AB，OE为∠COB的平分线，∠AOE的度数为_______.3.如下左图，BD与CE分别是∠ABC和∠ACB的平分线，如果∠DBC=∠ECB，那么∠ABC=∠ACB吗？_______.4.如上右图，OB是∠AOC的平分线，OD是∠COE的平分线，若∠AOC=70°，∠COE=40°,那么∠BOD=_______°.四、解答题：1、做一做：观察一下这副三角板每一个角的度数分别是多少度？下面是用三角板拼成的一些角，请你判断一下图中所示的角的度数，将它们的度数分别填在图下的括号中.你还能拼出其他度数的角吗？试一试.2、如图，OA是表示北偏东30°方向的一条射线，仿照这条射线画出表示下列方向的射线：(1) 南偏东25°； (2) 北偏西60°3．给你一张长方形纸片，不准使用其它工具，你能折出22.5°的角吗?亲手做一做,再和你的同学比一比. 4．如图，点O在直线AC上，画出∠COB的平分线OD。

编号9：角的度量与表示、角的比较姓名：一、角的度量与表示角的概念1角是由两条具有公共端点的组成的图形，这两条射线的公共端点叫做这个角的，这两条射线叫做角的。

构成两个角的基本条件：一是角的，二是角的。

角的表示方法角用几何符号“ ∠”表示，角的表示方法有三种：（1）一是由三个大写英文字母表示，如∠ AOB，其中A、B分别为两边上的一点，写在两边，可以交换位置，O是角的顶点，必须写在中间.（2）二是由一个大写英文字母表示，如∠ O，O是角的顶点，这种表示方法是在顶点O处只有一个角时才能使用。

（3）三是由一个阿拉伯数字或希腊字母表示，如∠ 1或∠α，用这种方法表示角时，要在靠近顶点处加上弧线，并注上阿拉伯数字或小写希腊字母。

1.角就是（）A、两条射线组成的图形B、有公共点的两条直线组成的图形C、有公共端点的两条射线组成的图形D、由一条直线旋转而成的图形2.用适当的方式分别表示下列各角：3.将图中的角用不同方法表示出来，并填写下表：角的概念2角也可以看成是由一条射线绕着它的端点旋转而成的图形。

平角、周角的概念一条射线绕它的端点旋转，当终边和始边成一条直线时，所成的角叫做平角。

终边继续旋转，当它又和始边重合时，所成的角叫做周角。

4.直角等于______度，平角等于_______度，周角等于_______度。

5.计算:⑴1.45°等于多少分? 等于多少秒?⑵1800″等于多少分? 等于多少度?6.在下图中，确定相应钟表上时针与分针所成的角度．7.如图，以O为顶点的角有几个？请表示出来．8.3点钟时,时针与分针所成的角度是_。

9.（1）每经过1时，时针转过度,每经过1分，分针转过度。

（2）9点时，时针和分针的夹角_________度。

（3）当时针指向上午10：30，时针和分针的夹角是______度。

二、角的比较10.角的分类：①②③11.观察一个公园的示意图：①海洋世界在大门的正东方向，你能说出它在大门的北偏东度。

《角的大小比较》资料知识要点1.角的定义：角是由两条射线共同起点形成的图形部分。

射线的起点称为角的顶点，两条射线称为角的边。

角一般用大写字母表示，如∠ABC.2.角的度量单位：角的大小可用度来度量，一个完整的圆周有360°。

也可用弧度来度量，一个完整的圆周有2π弧度。

3.角的种类：根据角的大小，角可以分为以下几种：a.锐角：度数小于90°或弧度小于π/2的角。

b.直角：度数为90°或弧度为π/2的角。

c.钝角：度数大于90°但小于180°或弧度大于π/2但小于π的角。

d.平角：度数为180°或弧度为π的角。

e.复角：度数介于180°和360°之间或弧度介于π和2π之间的角。

4.角的比较方法：a.角的比较可以通过度数或弧度来进行。

对于角α和角β来说，它们的大小关系可以通过以下几种情况来判断：i.如果α的度数小于β的度数，则α<β。

ii. 如果α的度数等于β的度数，则α=β。

iii. 如果α的度数大于β的度数，则α>β。

当用弧度来度量时，同样适用上述情况的推理方法。

b.通过数学运算进行角的比较：i.加法：若α<β，则α+γ<β+γ。

ii. 减法：若α<β，则α-γ<β-γ。

iii. 乘法：若α<β且γ>0，则αγ<βγ；若α<β且γ<0，则αγ>βγ。

iv. 除法：若α<β且γ>0，则α/γ<β/γ；若α<β且γ<0，则α/γ>β/γ。

5.角的比较法则：a.角的对立角相等：对于角α和β，如果α+β=180°或α+β=π，则α和β是对立角，它们的大小相等。

b.垂直角相等：对于由同一直线分割出来的两个相交角，它们是垂直角。

垂直角的度数之和等于180°或弧度之和等于π，所以它们是相等的。

c.角的平分线：对于一个角的平分线，它将该角分为两个相等的角。