概率与事件的关系

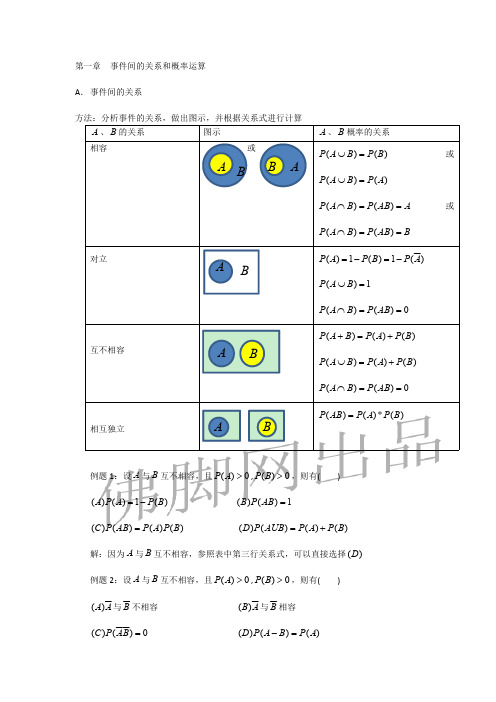
概率与事件的关系了解概率和事件的基本概念和关系概率与事件的关系：了解概率和事件的基本概念和关系概率和事件是数学中的重要概念，它们经常被用于统计学、经济学、工程学等多个领域。

概率是指某个事件发生的可能性，而事件则是指某个具体结果或一系列结果的集合。

本文将详细介绍概率和事件的基本概念以及它们之间的关系。

一、概率的基本概念1.1 概率的定义概率是用来描述某个事件发生的可能性大小的数值，一般用P(A)表示事件A发生的概率。

概率的取值范围是0到1，其中0表示不可能事件，1表示必然事件。

1.2 概率的性质（1）非负性：概率的取值范围是非负数，即P(A)≥0。

（2）规范性：某个样本空间中所有可能事件的概率之和为1，即P(Ω)=1。

（3）加法性：对于互斥事件（即事件A和事件B不可能同时发生），它们的概率可以相加，即P(A∪B)=P(A)+P(B)。

二、事件的基本概念2.1 事件的定义事件是指某个具体结果或一系列结果的集合，用A、B、C等字母表示。

事件可以是简单事件，即只包含一个结果的事件，也可以是复合事件，即包含多个结果的事件。

2.2 事件之间的关系（1）互斥事件：事件A和事件B是互斥事件，当且仅当它们不可能同时发生，即P(A∩B)=0。

（2）相互独立事件：事件A和事件B是相互独立事件，当且仅当它们的发生与否互不影响，即P(A∩B)=P(A)×P(B)。

三、概率与事件的关系概率与事件之间存在着紧密的关系，概率可以用来描述事件发生的可能性，而事件又是概率的基本对象。

概率可以通过事件的数量与样本空间的数量之比来计算，即P(A) = N(A) / N(Ω)其中，N(A)表示事件A包含的结果数量，N(Ω)表示样本空间中的结果数量。

在实际问题中，我们可以利用概率和事件的关系进行推理和预测。

通过观察和分析已有的数据，我们可以根据事件之间的关系和概率的性质，推断未来事件的可能性大小。

举个例子来说明概率和事件的关系。

概率事件的关系与运算知识点总结一、事件的关系。

1. 包含关系。

- 定义：如果事件A发生必然导致事件B发生，那么称事件B包含事件A，记作A⊆ B。

例如，在掷骰子试验中，设事件A=“掷出的点数为1”，事件B=“掷出的点数为奇数”，那么A发生时B一定发生，所以A⊆ B。

- 特殊情况：如果A⊆ B且B⊆ A，那么A = B，即这两个事件是同一个事件。

2. 互斥关系（互不相容关系）- 定义：如果事件A与事件B不能同时发生，即A∩ B=varnothing （varnothing为空集），那么称A与B是互斥事件。

例如，掷一枚硬币，事件A=“正面朝上”，事件B=“反面朝上”，A和B不可能同时发生，所以A与B互斥。

3. 对立关系。

- 定义：如果A∩ B=varnothing且A∪ B=varOmega（varOmega为样本空间），那么称A与B是对立事件，B叫做A的对立事件，记作B=¯A。

例如，在掷骰子试验中，设事件A=“掷出的点数为偶数”，事件B=“掷出的点数为奇数”，A∩ B=varnothing且A∪ B={1,2,3,4,5,6}（整个样本空间），所以A与B是对立事件。

- 关系：对立事件一定是互斥事件，但互斥事件不一定是对立事件。

4. 独立关系（如果涉及到选修内容）- 定义：设A,B是两个事件，如果P(AB)=P(A)P(B)，则称事件A与事件B相互独立。

例如，连续掷两次硬币，事件A=“第一次正面朝上”，事件B=“第二次正面朝上”，P(A)=(1)/(2)，P(B)=(1)/(2)，P(AB)=(1)/(4)，满足P(AB) = P(A)P(B)，所以A与B相互独立。

二、事件的运算。

1. 事件的并（和）运算。

- 定义：事件A与事件B的并（和）事件A∪ B是由所有A发生或B发生的基本事件组成的集合。

例如，掷骰子试验中，设事件A=“掷出的点数为1或2”，事件B=“掷出的点数为3或4”，那么A∪ B=“掷出的点数为1、2、3或4”。

概率计算与事件关系概率是数学中一个重要的分支，它研究的是事件发生的可能性。

概率计算是我们在日常生活中不可避免的一部分，我们可以利用概率计算来解决各种问题，从而更好地预测和决策。

概率计算的基本概念是事件的可能性。

事件可以是任何可能发生的事情，比如掷硬币的结果，买彩票中奖的概率，或者得到某种疾病的风险。

概率是用来描述事件发生的可能性的数值，通常在0到1之间。

如果一个事件的概率为0，表示这个事件不可能发生；如果一个事件的概率为1，表示这个事件一定会发生。

概率计算可以用来解决各种实际问题。

比如，在投资中，我们可以利用概率计算来预测某只股票的涨跌概率，从而做出更明智的投资决策。

在医学中，我们可以利用概率计算来评估某种疾病的风险，帮助医生更好地诊断和治疗疾病。

在工程中，我们可以利用概率计算来评估某种设计或者系统的可靠性，从而提高产品的质量。

概率计算涉及许多基本概念和方法。

其中一个基本概念是样本空间，它是指所有可能发生的结果的集合。

比如，掷一枚硬币，它的样本空间可以是{正面，反面}。

另一个基本概念是事件，它是样本空间的子集。

比如，在掷一枚硬币的例子中，正面朝上是一个事件。

概率可以通过计算事件发生的可能结果数目与样本空间中可能结果数目的比值来得到。

在概率计算中，还有一些常见的方法。

其中之一是加法规则，它用于计算两个事件的并的概率。

比如，事件A表示投掷一枚硬币正面朝上的概率，事件B表示投掷一枚硬币反面朝上的概率，那么事件A或事件B发生的概率可以用加法规则计算。

另一个常见的方法是乘法规则，它用于计算两个事件的交的概率。

比如，在抽取一张红色或者黑色扑克牌的例子中，事件A表示抽取一张红色牌的概率，事件B表示抽取一张黑色牌的概率，那么事件A和事件B同时发生的概率可以用乘法规则计算。

概率计算不仅仅可以用来预测结果，还可以帮助我们理解事件之间的关系。

例如，事件A和事件B是相互独立的，表示事件A的发生不会影响事件B的发生。

另外，事件A和事件B可以是互斥事件，表示事件A和事件B不能同时发生。

概率计算中的事件和与事件或关系在概率计算中，我们经常遇到各种事件，而了解事件之间的关系对于准确计算概率至关重要。

本文将详细讨论概率计算中的事件以及与事件“或”关系的相关内容。

一、事件的定义和表示方法在概率计算中，事件是指试验（随机现象）的一种结果或结果的集合。

事件通常用大写字母表示，比如A、B、C等。

例如，我们进行一次抛硬币的实验，正面朝上的结果就是一个事件，用A表示。

二、事件的包含关系1. 子事件：如果事件A发生，则事件B也一定发生，那么称事件B 是事件A的子事件。

用数学符号表示为A⊆B。

比如，当掷一个六面骰子时，事件A为出现奇数点数，事件B为出现大于等于4的点数，则事件A是事件B的子事件。

2. 互不相容事件：如果事件A和事件B没有共同的结果，即A∩B=Ø，则称事件A和事件B是互不相容的。

比如，掷一个六面骰子时，事件A为出现偶数点数，事件B为出现奇数点数，则A和B是互不相容的。

三、事件的并、或运算1. 事件的并运算：事件A和事件B的并，表示事件A或事件B至少发生一个。

用数学符号表示为A∪B。

比如，当掷一个六面骰子时，事件A为出现偶数点数，事件B为出现大于等于4的点数，则A∪B表示出现偶数点数或大于等于4的点数。

2. 事件的或运算：事件A和事件B的或，表示事件A和事件B都发生。

用数学符号表示为A∩B。

比如，当掷一个六面骰子时，事件A为出现偶数点数，事件B为出现大于等于4的点数，则A∩B表示既出现偶数点数又大于等于4的点数。

四、事件的计算方法1. 互不相容事件的概率计算：对于互不相容的事件A和事件B，它们的概率之和等于它们的并的概率。

即P(A∪B) = P(A) + P(B)。

比如，当掷一个六面骰子时，事件A为出现奇数点数，事件B为出现大于等于4的点数，则P(A∪B) = P(A) + P(B) = 3/6 + 3/6 = 1。

2. 一般事件的概率计算：对于一般事件A，我们可以利用事件A的子事件来计算其概率。

概率与事件关系概率是数学中的一个重要概念，它描述的是某件事情发生的可能性大小。

而事件是指我们所关注的事情或结果。

概率与事件之间存在着密切的关系，下面我们来探讨一下它们之间的联系。

首先，我们来了解一下概率的基本定义。

概率是一个介于0和1之间的数，表示某个事件发生的可能性大小。

通常用P(A)来表示事件A发生的概率，其中P代表概率。

如果一个事件发生的概率为0，那么这个事件是不可能发生的；如果概率为1，那么这个事件是肯定会发生的。

在实际问题中，我们通常通过统计或者实验来估算概率。

事件是我们所关心或所研究的对象，它可以是单个结果或一系列结果的集合。

我们可以将事件分为简单事件和复合事件。

简单事件是指只包含一个结果的事件，例如掷一次硬币正面朝上的事件；而复合事件是指包含多个结果的事件，例如掷两次硬币，至少有一枚硬币正面朝上的事件。

概率与事件之间的联系，可以通过概率公式来表示。

对于简单事件A来说，概率可以通过以下公式计算：P(A) = n(A)/n(S)，其中n(A)表示事件A中有多少个有利结果，n(S)表示在给定条件下所有可能结果的个数。

例如，在一副标准扑克牌中，红心K的概率为1/52，因为有且只有一张红心K，而总共有52张牌。

对于复合事件B来说，概率的计算稍微复杂一些。

复合事件可以通过求交集、并集、补集等运算来计算概率。

例如，对于掷两次硬币的复合事件C来说，至少有一枚硬币正面朝上的概率可以通过以下公式计算：P(C) = P(正正) + P(正反) + P(反正)，其中P(正正)表示两枚硬币都正面朝上的概率，P(正反)表示第一枚硬币正面朝上，第二枚硬币反面朝上的概率，P(反正)表示第一枚硬币反面朝上，第二枚硬币正面朝上的概率。

除了基本的概率公式之外，还有一些常见的概率规则可以用来计算复杂事件的概率。

其中包括加法法则、乘法法则和条件概率等。

加法法则指的是计算两个事件之和的概率；乘法法则指的是计算两个事件同时发生的概率；而条件概率是指在已知某个事件发生的条件下，另一个事件发生的概率。

条件概率与事件关系推导概率理论是数学中的一个重要分支，它研究随机事件的发生概率。

条件概率是概率理论中的一个重要概念，用于描述一个事件在给定另一个事件已经发生的条件下发生的概率。

在实际应用中，我们经常需要推导事件之间的关系，以便更好地理解和分析随机事件的发生概率。

本文将介绍条件概率的基本概念和推导方法，帮助读者更好地掌握条件概率与事件关系的推导。

条件概率是指在某个事件已经发生的条件下，另一个事件发生的概率。

用数学符号表示，假设事件A和事件B是两个随机事件，P(A|B)表示在事件B已经发生的条件下，事件A发生的概率。

根据概率的定义，我们可以将条件概率表示为：P(A|B) = P(A∩B) / P(B) （1）其中，P(A∩B)表示事件A和事件B同时发生的概率，P(B)表示事件B发生的概率。

根据上述公式，我们可以推导出一些常见的条件概率关系。

1. 乘法法则乘法法则是条件概率推导中的一个重要原理，用于计算两个事件同时发生的概率。

假设事件A和事件B是两个随机事件，根据乘法法则，可以推导出以下公式：P(A∩B) = P(B) * P(A|B) = P(A) * P(B|A) （2）通过以上公式，我们可以根据已知的概率信息计算出两个事件同时发生的概率。

这对于进行条件概率推导的问题非常有用。

2. 全概率公式全概率公式是条件概率推导中的另一个重要工具，用于计算一个事件的概率。

假设事件A是一个随机事件，事件B1、B2、B3、...是一组互斥且穷尽的事件，即B1、B2、B3、...两两不相交且它们的并集等于样本空间。

根据全概率公式，可以推导出以下公式：P(A) = P(A∩B1) + P(A∩B2) + P(A∩B3) + (3)通过以上公式，我们可以将事件A的概率表示为一系列条件概率相乘的形式，进而推导出事件A的实际概率。

3. 贝叶斯定理贝叶斯定理是条件概率推导中的一个重要定理，用于计算一个事件在另一个事件已经发生的条件下的条件概率。

概率计算与事件的关系概率是数学中重要的概念，它用于描述事件发生的可能性大小。

在现实生活中，我们常常需要计算概率来预测事情的发生可能性，进而做出合理的决策。

概率计算与事件的关系密切，本文将探讨概率计算与事件之间的关系，并介绍一些与概率计算相关的常见概念和方法。

一、概率的定义与性质概率是描述事件发生可能性的数值，通常用一个介于0和1之间的实数表示。

事件的概率越接近1，表示事件发生的可能性越大；概率越接近0，表示事件发生的可能性越小。

概率的定义具有以下几个性质：1. 非负性：概率必须大于等于0，即P(A) >= 0。

2. 规范性：对于一个必然事件（即一定会发生的事件），其概率为1，即P(S) = 1，其中S表示样本空间。

3. 互斥性：对于两个互斥事件A和B，即两个事件不可能同时发生，则它们的概率之和等于各自的概率之和，即P(A∪B) = P(A) + P(B)。

4. 有限可加性：对于任意一组互不相交的事件A₁，A₂，...，An，则它们的并事件的概率等于各个事件概率之和，即P(A₁∪A₂∪...∪An) = P(A₁) + P(A₂) + ... + P(An)。

以上是概率的一些基本性质，它们帮助我们理解和计算事件的概率。

二、计算概率的方法在实际计算中，我们需要了解一些常见的概率计算方法，其中包括了条件概率、乘法原理和加法原理。

1. 条件概率：条件概率是指在已知某个事件A发生的条件下，事件B发生的概率。

用P(B|A)表示条件概率，其计算公式为P(B|A) =P(A∩B)/P(A)。

其中，P(A∩B)表示事件A与事件B同时发生的概率，P(A)表示事件A发生的概率。

2. 乘法原理：乘法原理用于计算多个事件同时发生的概率。

当事件A和事件B相互独立时，它们同时发生的概率等于它们各自发生的概率的乘积，即P(A∩B) = P(A) × P(B)。

当事件A和事件B不相互独立时，乘法原理可以表示为P(A∩B) = P(A) × P(B|A)。

概率计算的事件关系概率是数学中一个重要的分支，它用于描述和预测事件的可能性。

在现实生活中，概率计算被广泛应用于各个领域，如科学、经济、统计学等。

本文将探讨概率计算的事件关系，并分析其在实际应用中的重要性。

概率的运算与事件关系密切相关。

事件是指可能发生或不发生的结果，而事件关系则用于描述不同事件之间的相互关系。

常见的事件关系包括“与”、“或”以及“非”等。

首先，我们来讨论一下“与”的事件关系。

当我们要计算两个事件同时发生的概率时，可以使用概率乘法规则。

该规则表示，如果事件A 和事件B是相互独立的，那么它们同时发生的概率等于它们各自发生的概率的乘积。

例如，假设我们有两个骰子，事件A表示第一个骰子掷出1的结果，事件B表示第二个骰子掷出2的结果。

那么同时掷出1和2的概率就是1/6乘以1/6，即1/36。

接下来，我们来讨论一下“或”的事件关系。

当我们要计算两个事件至少有一个发生的概率时，可以使用概率加法规则。

该规则表示，如果事件A和事件B是互斥的（即不能同时发生），那么它们至少有一个发生的概率等于它们各自发生的概率的和。

例如，假设我们有一个扑克牌的桥牌，事件A表示从中随机抽取一张梅花牌的结果，事件B 表示从中随机抽取一张红色牌的结果。

那么至少抽到一张梅花牌或一张红色牌的概率就等于13/52加上26/52，即39/52。

此外，还存在一种特殊的“或”的事件关系，即非互斥事件。

当我们要计算两个事件中至少一个发生的概率时，可以使用概率加法规则，但需要注意减去同时发生的概率。

例如，假设我们有一个标准的扑克牌组，事件A表示从中随机抽取一张红心牌的结果，事件B表示从中随机抽取一张A的结果。

那么至少抽到一张红心牌或一张A的概率就等于26/52加上4/52减去2/52（同时是红心和A的概率），即28/52。

除了上述常见的事件关系，还存在一种“非”的事件关系。

当我们要计算一个事件不发生的概率时，可以使用概率互补规则。

该规则表示，事件A不发生的概率等于1减去事件A发生的概率。