信息量和概率的关系

一、绪论11.模拟信号：是信号参量的取值是连续的或取无穷多个值的信号。

如机送出的语音信号、电视摄像机输出的图像信号等。

模拟信号有时也称连续信号，这个连续是指信号的某一参量可以连续变化或取无穷多个值，而不一定在时间上也连续。

2.数字信号：是信号参量只能取有限个值的信号。

如电报信号、计算机输入/输出信号、PCM 信号等。

数字信号有时也称离散信号，这个离散是指信号的某一参量是离散变化的，而不一定在时间上也离散。

3.通信系统的一般模型信源：是消息的产生地， 其作用是把各种消息转换成原始电信号(基带信号)。

机、电视摄像机和电传机、计算机等各种数字终端设备就是信源。

前者属于模拟信源，输出的是模拟信号；后者是数字信源，输出离散的数字信号。

发送设备：是将信源和信道匹配起来，即将信源产生的消息信号变换成适合在信道中传输的信号(如调制成已调信号）。

信道：是指传输信号的物理媒质。

在无线信道中，信道可以是大气（自由空间），在有线信道中，信道可以是明线、 电缆、波导或光纤。

噪声源：是通信系统中各种设备以及信道中噪声与干扰的集中表现。

接收设备：是完成发送设备的反变换，它的任务是从带有干扰的接收信号中正确恢复出相应的原始基带信号来。

信宿：是信息传输的归宿点，其作用是将复原的原始信号转换成相应的消息。

4.按照信道中传输的是模拟信号还是数字信号，可相应地把通信系统分为模拟通信系统和数字通信系统。

模拟通信系统：利用模拟信号来传递信息的系统。

分为模拟基带传输系统和模拟调制传输系统。

数字通信系统：利用数字信号来传递信息的系统。

分为数字基带传输系统和数字调制传输系统5.语音信号为300~3400Hz6.数字通信的优点：（1）抗干扰能力强，可消除噪声积累；（2）差错可控， 可以采用信道编码技术使误码率降低， 提高传输的可靠性；（3）易于与各种数字终端接口，用现代计算技术对信号进行处理、加工、变换、存储，从而形成智能网；（4） 易于集成化， 从而使通信设备微型化；（5） 易于加密处理， 且强度高。

信息量，信息熵1. 信息量的多与少任何事都会承载⼀定的信息量，包括已发⽣和未发⽣的事，只是它们承载的信息量有所不同。

如昨天下⾬这个已知事件，因为已经发⽣，你我都知道这件事，故它的信息量为0。

但明天会下⾬这件事，因为未发⽣，所以这事的信息量就⼤。

从上⾯例⼦可以看出信息量是⼀个与事件发⽣概率相关的概念，⼀条信息的信息量跟这个信息能解答的问题的不确定性有关。

⼀条信息能解答的问题越不确定，那它包含的信息量就越⼤。

如猜⼀个骰⼦最后向上的那⾯是多少点的游戏，这个游戏可能的情况有6种，但是猜32⽀球队中谁获得世界杯冠军的游戏则有32种可能。

所以“哪⽀球队最终获得世界杯冠军”的信息量⽐“骰⼦最后向上那⾯是多少点”的信息量⼤，因为前者是从32种可能中确定答案，⽽后者是从6种可能中确定答案。

2. 信息量的计算假设我错过了某年世界杯⽐赛，现在要去问⼀个知道⽐赛结果的朋友“哪⽀球队最终获得世界杯冠军”？他要求我猜，猜完会告诉我是对还是错，但我每猜⼀次就要给他⼀块钱。

那么我需要付给他多少钱才能知道谁是冠军？解：我可以把球队编号，从1到32，然后问“冠军的球队在1-16号中吗？”。

假如他告诉我对了，我就问“冠军的球队在1-8号中吗？”。

如果他告诉我不对，我就⾃然就知道冠军队在9-16号中。

这样我只需要猜5次就可以知道哪⽀球队是冠军了（思路类似于折半查找）所以，“谁是世界杯冠军”这个问题的答案的信息量只值5块钱。

⾹农⽤“⽐特”（bit）来作为信息量的单位。

像上边“谁是世界杯冠军”这个问题的答案的信息量是5⽐特。

如果是64⽀球队，“谁是世界杯冠军”这个问题的答案的信息量就是6⽐特，因为要多猜⼀次。

对⾜球了解的朋友看到这有疑问了，他觉得他不需要5次来猜。

因为他知道巴西，西班⽛，德国等这些强队夺冠的可能性⽐⽇本，韩国等球队⼤的多。

所以他可以先把强队分成⼀组，剩下的其它队伍⼀组。

然后问冠军是否在夺冠热门组⾥边。

重复这样的过程，根据夺冠的概率对剩下的候选球队分组，直⾄找到冠军队，这样也许三次或四次就猜出结果了。

通信原理考试第一章 绪论 1、信号是消息的载体。

2、模拟通信系统传输质量的度量准则主要是信噪比；数字通信系统传输质量的度量准则主要是错误判决的概率。

3、在数字通信系统中，可以采用纠错编码等差错控制技术，从而大大提高系统的抗干扰性。

4、5、衡量一个通信系统性能优劣的基本因素是有效性和可靠性。

有效性是指信道传输信息的速度快慢，可靠性则是指信道传输信息的准确程度。

6、模拟通信系统中用带宽衡量系统性能的有效性，用信噪比衡量系统性能的可靠性；数字通信系统的有效性用传输传输速率(或码元传输速率或者信息传输速率)衡量，可靠性用差错率(或误码率及误信率)衡量7.香农公式：)/1(log 2N S B C +=8.噪声按照来源分人为噪声和自然噪声两大类，其中自然噪声中的热噪声来自一切电阻性元器件中电子的热运动，热噪声无处不在，不可避免地存在于一切电子设备中。

9.噪声按性质分为脉冲噪声、窄带噪声和起伏噪声。

10.由于在一般的通信系统的工作频率范围内热噪声的频谱是均匀分布的，好像白光的频谱在可见的频谱范围内均匀分布那样，所以热噪声又常称为白噪声。

11.公式概率与信息量关系:)(log x p I a -= 二进制信息量:)(log 2x p I -=M MI M 22log /11log :-=-=进制每一码元信息量 离散独立非等概率的信息量: (1)平均信息量----信源熵)(log )()(21i Mi i x p x p x H ∑=-=比特/符号(2)总的信息量)(log )()(21i Mi i x p x p m x mH I ∑=-==(3)平均信息速率非等概率（也适用于等概率）()()b B R H x R = =⨯平均信息速率信源熵码元速率等概率2log b B R R M =【例1】已知彩色电视图象由1000000个象素组成。

设每个象素有64种彩色度。

每种彩色有16个亮度等级。

如果所有彩色度和亮度等级的组合机会均等，并统计独立，（1）试计算每秒传送100个画面所需的信息量；（2）如果接收机信噪比为30dB ，为了传送彩色图象所需信道带宽为多少？ ［正确答案］1）bit 109)1664(log 1010026=⨯⨯⨯2log ;()b B b B R R M R R ==⨯【评注】等概率信息速率非等概率也适用于等概率平均信息量2）B=C/(log2(1+S/N)=109/log2(1000)=108(Hz)2log (1/)C B S N =+【评注】香农公式：信道容量(即信道最大信息速率)【例2】 设某信息源的输出由A,B,C,D,E 五个符号组成，出现的概率分别为1/3, 1/4, 1/4, 1/12, 1/12。

信息熵是一种度量随机事件的不确定性或信息量的方法。

它用来衡量随机事件的复杂度和混乱程度，从而反映信息的实际价值。

信息熵的具体计算方法如下：对于每一个可能的结果，都要计算其发生概率。

对于每一个可能的结果，都要计算其对应的信息量。

这通常是采用对数函数计算，即以2为底的对数。

将每一个可能的结果的信息量乘以其发生概率，然后将所有的结果的信息量求和，即可得到信息熵的值。

对于每一个可能的结果，都要计算其发生概率。

在计算信息熵的过程中，首先需要计算每一个可能的结果的发生概率。

这是因为，发生概率与信息量是密切相关的，发生概率越大，信息量就越大。

因此，在计算信息熵时，必须首先确定每一个可能的结果的发生概率。

通常情况下，可以通过对事件发生的次数进行计数，来计算发生概率。

例如，如果有一个随机事件，其中有4种可能的结果，分别是A、B、C、D，且这4种结果在总共10次实验中对于每一个可能的结果，都要计算其发生概率。

在计算信息熵的过程中，首先需要计算每一个可能的结果的发生概率。

这是因为，发生概率与信息量是密切相关的，发生概率越大，信息量就越大。

因此，在计算信息熵时，必须首先确定每一个可能的结果的发生概率。

通常情况下，可以通过对事件发生的次数进行计数，来计算发生概率。

例如，如果有一个随机事件，其中有4种可能的结果，分别是A、B、C、D，且这4种结果在总共10次实验中分别发生了2次、3次、2次、3次，则它们的发生概率分别为0.2、0.3、0.2、0.3。

对于每一个可能的结果，都要计算其对应的信息量。

这通常是采用对数函数计算，即以2为底的对数。

在计算信息熵的过程中，需要计算每一个可能的结果的信息量。

这是因为，信息量与发生概率是密切相关的，发生概率越大，信息量就越大。

因此，在计算信息熵时，必须首先确定每一个可能的结果的信息量。

通常情况下，信息量是采用对数函数计算的，即以2为底的对数。

这是因为，在计算信息量时，需要考虑信息的不确定性，而以2为底的对数可以很好地反映信息的不确定性。

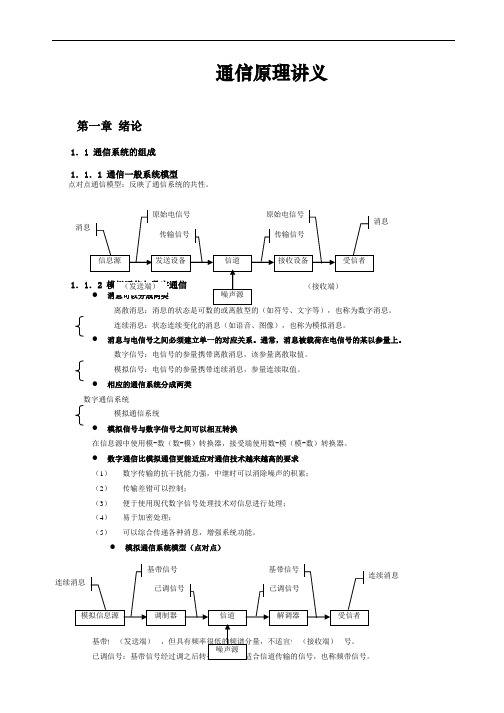
通信原理讲义第一章绪论1．1 通信系统的组成1．1．1 通信一般系统模型点对点通信模型：反映了通信系统的共性。

连续消息：状态连续变化的消息（如语音、图像），也称为模拟消息。

●消息与电信号之间必须建立单一的对应关系。

通常，消息被载荷在电信号的某以参量上。

数字信号：电信号的参量携带离散消息，该参量离散取值。

模拟信号：电信号的参量携带连续消息，参量连续取值。

●相应的通信系统分成两类数字通信系统模拟通信系统●模拟信号与数字信号之间可以相互转换在信息源中使用模-数（数-模）转换器，接受端使用数-模（模-数）转换器。

●数字通信比模拟通信更能适应对通信技术越来越高的要求（1）数字传输的抗干扰能力强，中继时可以消除噪声的积累；（2）传输差错可以控制；（3）便于使用现代数字信号处理技术对信息进行处理；（4）易于加密处理；（5）可以综合传递各种消息，增强系统功能。

●模拟通信系统模型（点对点）调制器：将基带信号转变为频带信号的设备。

解调器：将频带信号转变为基带信号的设备。

模拟通信强调变换的线性特性，既已调参量与基带信号成比例。

● 数字通信系统模型（点对点） 强调已调参量与基带信号之间的一一对应。

数字通信需要解决的问题：（2） 编码与解码：通过差错控制编码消除噪声或干扰造成的差错； （3） 加密和解密：对基带信号进行人为“搅乱”；（4） 同步：发送和接收节拍一致，包括：位同步（码元同步）和群同步、帧同步、句同步或码组同步。

数字通信模型：1．2 通信系统的分类及通信方式 1．2．1 通信系统分类● 按消息的物理特征分类电报通信系统 电话通信系统 数据通信系统图像通信系统 ● 按调制方式分类基带传输线性调制载波调制 非线性调制 频带传输 数字调制脉冲模拟调制脉冲调制消息 消息消息消息脉冲数字调制●按信号特征分类模拟通信系统数字通信系统●按传输媒介分类有线无线1．2．2 通信方式分类●点对点通信，按传送方向与时间关系：单工通信：消息只能单方向传输半双工通信：通信双方都能收发消息，但不能同时进行收发全双工通信：通信双方可同时进行收发●数字通信中，按数据信号码元排列方式：串行传输：数字信号码元序列按时间顺序一个接一个的在信道中传输，适合远距离传输。

227随着我国科学技术的不断创新与发展，概率论与数理统计作为一门课程，在灵活运用中能够协助我们从海量数据中发现规律，并深入挖掘数据的潜在价值。

通过将大数据分析技术引入概率论与数理统计课程，我们可以探索不同数据之间的关系，并展示数据的意义。

通过使用概率统计中随机数据的演绎和归纳理念来分析海量数据间的联系，可以更清晰地实现理论与实践的结合，帮助学生更容易地掌握这门学科。

这种教学方法基于作者多年的教学经验和对大数据的认识和理解。

同时，该方法也考虑到学生自身发展的实际需求，并符合数字化时代发展的理念。

基于上述背景，文中提出了基于大数据分析能力的概率论与数理统计课程的教学改革策略。

这些策略旨在为今后概率统计课程的发展提供借鉴，并帮助学生更好地适应数字化时代的需求。

一、概率论与数理统计课程教学目标基于大数据分析能力的概率论与数理统计课程，其教学改革旨在适应大数据、人工智能等信息化技术的发展，培养学生深入挖掘数据价值的潜在能力，让他们能将大数据技术应用到更广泛的行业领域。

该课程的教学目标主要体现在以下几个层面：第一，整合专业相关的大数据技术应用案例：针对不同专业的教师和学生，需要收集和汇总与各个专业相关的大数据技术应用案例，并将这些案例有机地融入概率论与数理统计课程中，使学生能够将理论知识应用于实际问题。

第二，采用线上和线下相结合的教学模式：通过开设“微课”、MOOC 等线上学习资源，结合线下的理论学习，学生可以拓展眼界、开阔思维，并提升自主学习能力。

基于大数据分析能力的概率论与数理统计课程教学改革研究第三，建立多样化的考核评价制度：当前许多高校的概率论与数理统计课程的考核内容主要集中在理论知识的了解层面，对实践应用的考核较少，甚至没有考核。

在改革课程考核制度时，可以借鉴数学模型的构建形式，要求学生将概率统计相关的理论知识运用到论文中，以展示他们对知识的掌握程度，并提升他们的课程实践能力。

第四，整合数据统计软件：将数据统计软件与概率论与数理统计课程相融合。

第二章信息的度量2.1信源在何种分布时，熵值最大？又在何种分布时，熵值最小？答：信源在等概率分布时熵值最大；信源有一个为1，其余为0时熵值最小。

2.2平均互信息量I(X;Y)与信源概率分布q(x)有何关系？与p(y|x)又是什么关系？答：若信道给定，I(X;Y)是q(x)的上凸形函数；若信源给定，I(X;Y)是q(y|x)的下凸形函数。

2.3熵是对信源什么物理量的度量？答：平均信息量2.4设信道输入符号集为{x1,x2,……xk}，则平均每个信道输入符号所能携带的最大信息量是多少？答：kk k xi q xi q X H i log 1log 1)(log )()(2.5根据平均互信息量的链规则，写出I(X;YZ)的表达式。

答：)|;();();(Y Z X I Y X I YZ X I 2.6互信息量I(x;y)有时候取负值，是由于信道存在干扰或噪声的原因，这种说法对吗？答：互信息量)()|(log );(xi q yj xi Q y x I ，若互信息量取负值，即Q(xi|yj)<q(xi)，说明事件yi 的出现告知的是xi 出现的可能性更小了。

从通信角度看，视xi 为发送符号，yi 为接收符号，Q(xi|yj)<q(xi)，说明收到yi 后使发送是否为xi 的不确定性更大，这是由于信道干扰所引起的。

2.7一个马尔可夫信源如图所示，求稳态下各状态的概率分布和信源熵。

答：由图示可知：43)|(41)|(32)|(31)|(41)|(43)|(222111110201s x p s x p s x p s x p s x p s x p 即：43)|(0)|(41)|(31)|(32)|(0)|(0)|(41)|(43)|(222120121110020100s s p s s p s s p s s p s s p s s p s s p s s p s s p 可得：1)()()()(43)(31)()(31)(41)()(41)(43)(210212101200s p s p s p s p s p s p s p s p s p s p s p s p得：114)(113)(114)(210s p s p s p )]|(log )|()|(log )|()[()]|(log )|()|(log )|()[()]|(log )|()|(log )|()[(222220202121211111010100000s s p s s p s s p s s p s p s s p s s p s s p s s p s p s s p s s p s s p s s p s p H 0.25（bit/符号）2.8一个马尔可夫信源，已知：0)2|2(,1)2|1(,31)1|2(,32)1|1(x x p x x p x x p x x p 试画出它的香农线图，并求出信源熵。

认证认可业务信息统一查询平台
中国认证认可信息网是经国家认证认可监督管理委员会授权，由国家认证认可监督管理委员会信息中心主办的认证认可行业门户网站。

以下是店铺为大家整理的关于认证认可业务信息统一查询平台，给大家作为参考，欢迎阅读!
认证认可业务信息统一查询平台点击进入↓↓↓
信息特点
别担心，信息虽然是不确定的，但还是有办法将它们进行量化的。

人们根据信息的概念，可以归纳出信息是有以下的几个特点的：
1. 消息x发生的概率P(x)越大，信息量越小;反之，发生的概率越小，信息量就越大。

可见，信息量(我们用I来表示)和消息发生的概率是相反的关系。

2. 当概率为1时，百分百发生的事，地球人都知道，所以信息量为0。

3. 当一个消息是由多个独立的小消息组成时，那么这个消息所含信息量应等于各小消息所含信息量的和。

根据这几个特点，如果用数学上对数函数来表示，就正好可以表示信息量和消息发生的概率之间的关系式：I=-loga(P(x))。

这样，信息不就可以被量化了吗?既然信息可以被量化，那么总得给它一个单位吧?人的体重是以公斤来计量的，人的身高是以米来计量的，那么信息量该以什么单位来计量呢?通常是以比特(bit)为单位来计量信息量的，这样比较方便，因为一个二进制波形的信息量恰好等于1bit。

息论的创始人是美贝尔电话研究所的数学家申农（C.E.Shannon1916——），他为解决通讯技术中的信息编码问题，突破发老框框，把发射信息和接收信息作为一个整体的通讯过程来研究，提出发通讯系统的一般模型；同时建立了信息量的统计公式，奠定了信息论的理论基础。

1948年申农发表的《通讯的数学理论》一文，成为信息论诞生的标志。

申农创立信息论，是在前人研究的基础上完成的。

1922年卡松提出边带理论，指明信号在调制（编码）与传送过程中与频谱宽度的关系。

1922年哈特莱发表《信息传输》的文章，首先提出消息是代码、符号而不是信息内容本身，使信息与消息区分开来，并提出用消息可能数目的对数来度量消息中所含有的信息量，为信息论的创立提供了思路。

美国统计学家费希尔从古典统计理论角度研究了信息理论，苏联数学家哥尔莫戈洛夫也对信息论作过研究。

控制论创始人维纳建立了维纳滤波理论和信号预测理论，也提出了信息量的统计数学公式，甚至有人认为维纳也是信息论创始人之一。

在信息论的发展中，还有许多科学家对它做出了卓越的贡献。

法国物理学家L.布里渊（L.Brillouin）1956年发表《科学与信息论》专著，从热力学和生命等许多方面探讨信息论，把热力学熵与信息熵直接联系起来，使热力学中争论了一个世纪之久的“麦克斯韦尔妖”的佯谬问题得到了满意的解释。

英国神经生理学家（W.B.Ashby）1964年发表的《系统与信息》等文章，还把信息论推广应用芋生物学和神经生理学领域，也成为信息论的重要著作。

这些科学家们的研究，以及后来从经济、管理和社会的各个部门对信息论的研究，使信息论远远地超越了通讯的范围。

信息论-信息概念信息科学是以信息为主要研究对象，以信息的运动规律和应用方法为主要研究内容，以计算机等技术为主要研究工具，以扩展人类的信息功能为主要目标的一门新兴的综合性学科。

信息科学由信息论、控制论、计算机科学、仿生学、系统工程与人工智能等学科互相渗透、互相结合而形成的。

通信的基本概念通信：所谓通信就是信息的传递。

消息：通常指有具体的内容的文字、符号、数据、语音、图片、图像等。

消息是信息的具体表现形式，是各种特定的信息。

信息：是消息的统称，是消息的抽象和概括。

通信的基本目的：把信息大量地、快速地、准确地、广泛地、方便地、经济地、安全地（即：多、快、好、广、便、省、安）从信源通过传输介质传送到信宿。

通信系统通信系统：用于进行通信的设备硬件、软件和传输介质的集合叫做通信系统。

模拟通信系统：指的是信源、信宿和信道处理的都是模拟信号的通信系统。

数字通信系统：指信源、信宿处理的是模拟信号，而信道为数字信道的通信系统。

数据通信系统：是随计算机和计算机网络的发展而出现的一种新的通信概念，它是指信源、信宿处理的是数字信号，而信道既可以为数字信道也可以是模拟信道的通信，主要指计算机之间的通信系统。

基带通信系统：所谓基带通信指的是以基带信号（指没有经过任何调制处理的信号）作为传输信号的通信系统。

调制通信系统：调制通信系统是传输已调信号的通信系统。

无线通信系统：利用无线电波、红外线、超声波、激光进行通信的系统统称为无线通信系统。

有线通信系统：用导线（包括电缆、光缆和波导等）作为介质的通信系统就是有线通信系统。

数字通信系统的优点：①抗干扰能力强。

②便于进行信号加工与处理。

③传输中出现的差错（误码）可以设法控制，提高了传输质量。

④数字信息易于加密且保密性强。

信息是可以量化的，也就是说信息是可以度量的。

信息量的大小与事件出现的概率成反比关系：多路复用的基本概念多路复用：所谓多路复用就是在同一个物理信道（如一个无线电频段、一个无线电频率、一对线缆、一条光纤等）中利用特殊技术传输多路信号，即在一条物理信道内产生多个逻)(log )(1log x P x P I a a -==)1(log 2NS B C +=辑信道，每个逻辑信道传送一路信号。

目前常用的复用技术主要有：频分复用技术、时分复用技术、空分复用技术、码分复用技术、波分复用技术。

浅谈信息论及其应用摘要本文主要研究了信息论的起源、信息论的分类、信息论研究的主要内容以及信息论在现实生活中的运用，信息论是运用概率论与数理统计的方法研究信息信息熵通信系统数据传输密码学数据压缩等问题的应用数学学科。

主要介绍信息论在数据压缩、密码学、统计及信号处理中的应用。

关键字：信息论数据压缩密码学一、信息论的起源随着社会的发展，科学技术的不断进步，近些年信息论，控制论和系统论被作为一种新的理论方法，在社会科学各个领域中被加以尝试和运用。

信息反馈控制机制稳定性等大量新概念和新名词被人们所接受，并涌进许多传统的社会科学领域这是一场方法论的革命，为社会科学各个领域带来了朝气。

信息论最早是美国研究所（信息论之父）克劳德·申农提出[1]，他于1948年10月发表于贝尔系统技术学报上的论文《通信的数学原理》作为现代信息论研究的开端。

二、信息论的定义与分类（一）定义[2]1.申农认为信息论是：通讯的基本问题就是精确地或近似地在一端复现在另一端所挑选的信号。

2.信息论是关于信息的本质和传送规律的科学理论，是研究信息的计量、发送、传递、交换、接收和储存的一门新兴科学。

（二）分类1. 狭义信息论：是用统计学的方法研究通讯系统中存在的信息传递和处理的规律的科学。

2. 广义信息论：是用数学和其他有关科学的方法研究一切现实系统中存在的信息传递、处理识别和利用的共同规律的科学。

三、信息论研究的基本内容实际通信系统比较复杂，但是任何通信系统都可以抽象为信息源发送机信道接收机收信者，因此，通信过程中信息的定量表示信源和信宿信道和信道容量编码和译码等方面的问题，就构成了信息论的基本内容。

信息论是运用概率论与数理统计的方法研究信息信息熵通信系统数据传输密码学数据压缩等问题的应用数学学科。

信息论将信息的传递作为一种统计现象来考虑，给出了估算通信信道容量的方法。

信息传输和信息压缩是信息论研究中的两大领域这两个方面又由信息传输定理信源信道隔离定理相互联系[3]。

通信原理试卷一填空题1.接收设备的功能是将和。

信号放大,反变换2.受信者是传送信息的，其功能与相反。

目的地, 信源3.基带的含义是指信号的频谱从附近开始，如话音信号的频率范围为。

零频,300Hz-3400Hz4.经过调制以后的信号称为已调信号，有两个基本特征：一是；二是。

携带有信息,适应在信道中传输5.同步是使两端的信号在上保持步调一致。

收发, 时间6.在数据通信中，按数据代码排列的方式不同，可分为和。

并行传输, 串行传输7.通信中的和都可看作随时间变化的随机过程。

信号,噪声8.随机过程具有和的特点。

随机变量,时间函数9.一个随机过程的与无关，则称其为严平稳过程。

统计特性, 时间起点10.若一个过程是严平稳的，则它广义平稳的，反之。

必是,不一定成立11.若一个过程的等于对应的，则该过程是各态历经的。

时间平均,统计平均12.若一个过程是各态历经的，则它平稳的，反之。

也是,不一定成立13.无线信道按传输方式区分基本上有、和视线传播三种。

地波, 天波14.有线信道分为和两大类。

有线电信道, 有线光信道15.信道的数学模型分为模型和模型。

调制信道,编码信道16.由连续信道容量的公式得知：、是容量的决定因素。

带宽, 信噪比17.调制信道模型用和表示信道对信号传输的影响。

加性干扰,乘性干扰18.模拟调制分为：和。

幅度调制, 角度调制19.SSB信号只传输DSB信号中的一个边带，所以频谱，效率。

最窄, 最高20.VSB是与之间的一种折中方式。

DSB, SSB21.调制方法分为：和。

相干解调, 非相干解调22.FDM是一种按来划分的复用方式。

频率, 信道23.的非相干解调和的非相干解调一样，都存在“门限效应”。

FM信号, AM信号24.多路复用是指在信道中同时传输信号。

一条, 多路25.基带信号的特征是将其频谱从开始，占据的频带。

零频或很低频率, 较宽26.对基带信号传输前的处理或变换的目的是使与相匹配。

信号的特性,信道的传输特性27.数字基带传输系统中，造成误码的两个主要因素是和。