2014年高三一模客观压轴题汇编(3)

2014高考数学压轴题一1．（12分）已知抛物线、椭圆和双曲线都经过点()1,2M ，它们在x 轴上有共同焦点，椭圆和双曲线的对称轴是坐标轴，抛物线的顶点为坐标原点.（Ⅰ）求这三条曲线的方程；（Ⅱ）已知动直线l 过点()3,0P ，交抛物线于,A B 两点，是否存在垂直于x 轴的直线l '被以AP 为直径的圆截得的弦长为定值？若存在，求出l '的方程；若不存在，说明理由.解：（Ⅰ）设抛物线方程为()220y px p =>，将()1,2M 代入方程得2p =24y x ∴= 抛物线方程为: ………………………………………………（1分）由题意知椭圆、双曲线的焦点为()()211,0,1,0,F F -∴ c=1…………………（2分） 对于椭圆，()()222122112114222a MF MF =+=+++-+=+()222222212123222221322222a ab ac x y ∴=+∴=+=+∴=-=+∴+=++ 椭圆方程为：………………………………（4分）对于双曲线，122222a MF MF '=-=-222222213222221322222a abc a x y '∴=-'∴=-'''∴=-=-∴-=-- 双曲线方程为：………………………………（6分）（Ⅱ）设AP 的中点为C ，l '的方程为：x a =，以AP 为直径的圆交l '于,D E 两点，DE 中点为H令()11113,,,22x y A x y +⎛⎫∴ ⎪⎝⎭ C ………………………………………………（7分） ()()22111111322312322DC AP x y x CH a x a ∴==-++=-=-+()()()2222221112121132344-2324622222DH DC CH x y x a a x a aa DH DE DH l x ⎡⎤⎡⎤∴=-=-+--+⎣⎦⎣⎦=-+==-+=∴=='= 当时,为定值; 为定值此时的方程为： …………（12分）2．（14分）已知正项数列{}n a 中，16a =，点()1,n n n A a a +在抛物线21yx =+上；数列{}n b 中，点(),n n B n b 在过点()0,1，以方向向量为()1,2的直线上.（Ⅰ）求数列{}{},n n a b 的通项公式；（Ⅱ）若()()()n na f nb ⎧⎪=⎨⎪⎩, n 为奇数, n 为偶数，问是否存在k N ∈，使()()274f k f k +=成立，若存在，求出k 值；若不存在，说明理由； （Ⅲ）对任意正整数n ，不等式11202111111n n nn a a n a b b b +-≤⎛⎫⎛⎫⎛⎫-++++ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭成立，求正数a 的取值范围.解：（Ⅰ）将点()1,n n n A a a +代入21y x =+中得()11111115:21,21n n n n n n a a a a d a a n n l y x b n ++=+∴-==∴=+-⋅=+=+∴=+ 直线 …………………………………………（4分）（Ⅱ）()()()521n f n n ⎧+⎪=⎨+⎪⎩, n 为奇数, n 为偶数………………………………（5分）()()()()()()27274275421,42735227145,24k k f k f k k k k k k k k k k ++=∴++=+∴=+∴++=+∴==当为偶数时，为奇数， 当为奇数时，为偶数，舍去综上，存在唯一的符合条件。

2014年高三一模客观压轴题汇编（学生版）填空题1.（2014年普陀一模文理12）已知全集}8,7,6,5,4,3,2,1{=U ，在U 中任取四个元素组成的集合记为 },,,{4321a a a a A =，余下的四个元素组成的集合记为},,,{4321b b b b A C U =， 若43214321b b b b a a a a +++<+++，则集合A 的取法共有 种2.（2014年普陀一模文理14） 已知函数⎩⎨⎧<+≥-=0),1(0,2)(x x f x a x f x ，若方程0)(=+x x f 有且仅有两个解，则实数a 的取值范围是3.（2014年长宁一模文14）设a 为非零实数，偶函数1||)(2+-+=m x a x x f (x R )在区间(2,3)上存在唯一零点，则实数a 的取值范围是变式：函数2()4f x x x a =-+在(0,3)上有一个零点，则实数a 的取值范围是4.（2014年长宁一模理14）定义：{}123min ,,,,n a a a a 表示123,,,,n a a a a 中的最小值．若定义()f x ={}2min ,5,21x x x x ---，对于任意的n *∈N ，均有(1)(2)(21)(2)()f f f n f n kf n +++-+≤成立，则常数k 的取值范围是5.（2014年嘉定一模理13文14）已知函数⎪⎩⎪⎨⎧<++-≥++=0,,0,12)(22x c bx x x x ax x f 是偶函数，直线t y =与函数 )(x f 的图像自左至右依次交于四个不同点A 、B 、C 、D ，若||||BC AB =，则实数t 的值为6.（2014年嘉定一模理14）某种平面分形图如下图所示，一级分形图是一个边长为1的等边三角形（图（1））；二级分形图是将一级分形图的每条线段三等分，并以中间的那一条线段为一底边向形外作等边三角形， 然后去掉底边（图（2））；将二级分形图的每条线段三等边，重复上述的作图方法，得到三级分形图 （图（3））；…；重复上述作图方法，依次得到四级、五级、…、n 级分形图．则n 级分形图的 周长为7.（2014年静安一模理12）图（1） 图（2） 图（3）……8.（2014年静安一模理14）9.（2014年闸北一模理9）设0,1a a >≠，已知函数()2sin 22,(0)x f x a x x π=+->至少有5个零点，则a 的取值范围为变式练习（2014年闸北区一模文科9）设1,0≠>a a ，函数2|2sin |2)(-+=x a x f xπ（0>x ）有四个零点，则a 的值为10. （2014年闸北一模理10）设曲线22:23()C x y x y ++=+，则曲线C 所围封闭图形的面积为变式练习（2014年闸北区一模文科10）由曲线||||22y x y x +=+所围成的封闭图形的面积为11.（2014年宝山一模理14） 关于函数()1x f x x =-，给出下列四个命题：①当0x >时，()y f x =单调递减且没有最值；②方程()(0)f x kx b k =+≠一定有解；③如果方程()f x k =有解，则解的个数一定是偶数； ④()y f x =是偶函数且有最小值； 则其中真命题是12. （2014年闵行一模理12）设,i j 依次表示平面直角坐标系x 轴、y 轴上的单位向量， 且25a i a j -+-=，则2a i +的取值范围是13.（2014年闵行一模理13）22log (04)()2708(4)33x x f x x x x ⎧<≤⎪=⎨-+>⎪⎩，若,,,a b c d 互不相同， 且()()()()f a f b f c f d ===，则abcd 的取值范围是 变式练习（2014年闵行区一模文科13）已知函数()11f x x =--，若关于x 的方程()f x t =()t R ∈恰有四个 互不相等的实数根1234,,,x x x x （1234x x x x <<<），则1234x x x x ++⋅的取值范围是14.（2014年闵行一模理14）211,1k A x x kt t kt k ⎧⎫==+≤≤⎨⎬⎩⎭，其中2,3,......,2014k =， 则所有k A 的交集为变式练习（2014年闵行区一模文14）已知42421()1x kx f x x x ++=++（k 是实常数），则()f x 的最大值与最小值的乘积 为15.（2014年徐汇一模理12）如图所示，已知点G 是△ABC 的重心，过G 作直线与AB 、AC 两边分别交于M 、N 两点，且,AM x AB AN y AC ==，则xyx y+的值为16.（2014年徐汇一模理13） 一个五位数abcde 满足,,,a b b c d d e <>><且,a d b e >>(如37201,45412)，则称这个五位数符合“正弦规律”.那么，共有 个五位数符合“正弦规律”17.（2014年徐汇区一模理科14）定义区间(),c d 、[),c d 、(],c d 、[],c d 的长度均为()d c d c ->. 已知实数(),a b a b >.则满足111x a x b+≥--的x 构成的区间的长度之和为18.（2014年松江一模理11）对于任意实数x ，x 表示不小于x 的最小整数，如1.22,0.20=-=．定义在R 上的函数()2f x x x =+，若集合{}(),10A y y f x x ==-≤≤，则集合A 中所有元素的和为19.（2014年松江一模理13）已知函数()log 1(0,1)a f x x a a =->≠，若1234x x x x <<<， 且12()()f x f x =34()()f x f x ==，则12341111x x x x +++=20.（2014年松江一模理14） 设集合{1,2,3,,}A n =，若B ≠∅且B A ⊆，记()G B 为B 中元素的最大值与最小值之和，则对所有的B ，()G B 的平均值＝21.（2014年青浦一模理13）已知直角坐标平面上任意两点11(,)P x y 、22(,)Q x y ，定义212121212121(,)x x x x y y d P Q y y x x y y ⎧--≥-⎪=⎨--<-⎪⎩为,P Q 两点的“非常距离”，当平面上动点(,)M x y到定点(,)A a b 的距离满足3MA =时，则(,)d M A 的取值范围是22.（2014年青浦一模理14）若不等式1(1)(1)31n na n +--<++对任意自然数n 恒成立，则实数a 的取值范围是23（2014年金山一模理13）如图，已知直线:4360l x y -+=，抛物线2:4C y x =图像上的一个 动点P 到直线l 与y 轴的距离之和的最小值是24.（2014年金山一模理14）在三棱锥P ABC -中，PA 、PB 、PC 两两垂直，且3,2,1PA PB PC ===.设M 是底面ABC 内一点，定义()(,,)f M m n p =，其中m 、n 、p 分别是三棱锥M PAB -、三棱锥M PBC -、三棱锥M PCA -的体积。

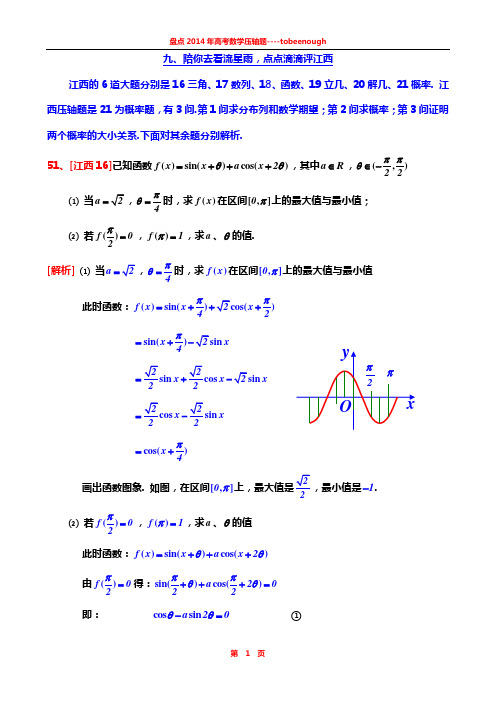
九、陪你去看流星雨，点点滴滴评江西江西的6道大题分别是16三角、17数列、18、函数、19立几、20解几、21概率. 江西压轴题是21为概率题，有3问.第1问求分布列和数学期望；第2问求概率；第3问证明两个概率的大小关系.下面对其余题分别解析.51、[江西16]已知函数f x x a x 2()sin()cos()θθ=+++，其中a R ∈，22(,)ππθ∈-⑴当a =4πθ=时，求f x ()在区间0[,]π上的最大值与最小值；⑵ 若f 02()π=，f 1()π=，求a 、θ的值.[解析] ⑴当a =4πθ=时，求f x ()在区间0[,]π上的最大值与最小值此时函数：f x x x 42()sin())ππ=+++x x 4sin()π=+x x x 22sin =+-x x 22cos =- x 4cos()π=+画出函数图象. 如图，在区间0[,]π1-. ⑵ 若f 02()π=，f 1()π=，求a 、θ的值此时函数：f x x a x 2()sin()cos()θθ=+++由f 02()π=得：a 2022sin()cos()ππθθ+++=即： a 20cos sin θθ-= ①由f 1()π=得：a 21sin()cos()πθπθ+++= 即： a 21sin cos θθ--= ② 由①×①得：222a 22a 20cos sin cos sin θθθθ+-= ③ 由②×②得：222a 22a 21sin cos sin cos θθθθ++= ④ 由③＋④得：2a 2a 220(sin cos cos sin )θθθθ+-= 即：2a 2a 20sin()θθ+-=，即：a a 20(sin )θ-= 故：a 0=或 a 2sin θ= 将a 0=代入①、②式得：2πθ=-，这与22(,)ππθ∈-不符，故：2πθ≠- 则：a 2sin θ= ⑤将⑤式代入①式得：220cos sin sin θθθ-=，即：240cos sin cos θθθ-= 即：2140cos (sin )θθ-=，即：0cos θ= ⑥ 或2140sin θ-=，即：12sin θ= ⑦ 或：12sin θ=-⑧ 由⑥式得： 2k 2πθπ=±+，由于不满足22(,)ππθ∈-，故⑥式舍. 将⑤⑦式代入②式得： 1212cos θ--=， 即：322cos θ-=，由于不满足21cos θ≤，故⑦式舍. 将⑤⑧式代入②式得：1212cos θ+=，即：122cos θ= ⑨ 由⑧⑨式和22(,)ππθ∈-得：6πθ=-，代入⑤式得：a 1=-本题答案：⑴ 最大值是2，最小值是1-； ⑵ 6πθ=-，a 1=-.52、[江西17]已知首项都是1的两个数列{}n a 、{}n b （n b 0≠，n N +∈），满足n n 1n 1n n 1n a b a b 2b b 0+++-+=.⑴ 令nn na cb =，求数列{}n c 的通项公式； ⑵ 若n 1n b 3-=，求数列{}n a 的前n 项和n S . [解析] ⑴ 令nn na cb =，求数列{}n c 的通项公式 由n n 1n 1n n 1n a b a b 2b b 0+++-+=除以n 1n b b +得：n n 1n n 1a a 20b b ++-+= 即：n n 1c c 20+-+=，即：n 1n c c 2+-= ① 且：111a c 1b == ② ①②表明：{}n c 是一个首项为1，公差为2的等差数列. 故：n c 2n 1=- ③⑵ 若n 1n b 3-=，求数列{}n a 的前n 项和n S 由nn na c 2n 1b ==-得：n 1n n a 2n 1b 2n 13()()+=-=-⋅ ④ 故数列{}n a 前n 项和n S 为：0123n 1n S 133353732n 13...()-=⋅+⋅+⋅+⋅++-⋅ ⑤ 1234n n 3S 133353732n 13...()=⋅+⋅+⋅+⋅++-⋅ ⑥由⑤-⑥得：0123n 1n n 2S 132********n 13...()--=⋅+⋅+⋅+⋅++⋅--⋅0123n 10n 233333132n 13(...)()-=⋅+++++-⋅--⋅n0n 1323132n 1313()()-=⋅⋅-⋅--⋅-n n 3112n 13()()=----⋅ n 22n 23()=---故：n n S n 131()=-⋅+本题答案：⑴ n c 2n 1=-；⑵ n n S n 131()=-⋅+.本题第⑵问，网上由好多都写错，写成n 1n b 3+=，应更正为：n 1n b 3-=.53、[江西18] 已知函数2f x x bx b ()(=++b R ∈）.⑴当b 4=时，求f x ()的极值；⑵若f x ()在区间103(,)上单调递增，求b 的取值范围.[解析] ⑴ 当b 4=时，求f x ()的极值此时函数为：2f x x 4x 4x 2()(()=++=+ ① 函数的定义域为：1x 2<令：t x 2=+，则：x t 2=-，代入①式得：f t t t 2()==② 由均值不等式n n A G ≥得：12222222222255a b c d e a b c d e abcde 5()()++++≥=25≥即：2510t 5(≥，即：52t 2≤= ③代入②式得：f t t 422()=≤= ④由于②式中f t t 0()==≥ ⑤ 由④⑤式得本题极值为：极大值4，在t 104t =-时得到，即：1t 2=，即：11x t 20=-=时得到； 极小值0，在t 0=时得到，即：2t 0=，即：22x t 22=-=-时得到.⑵ 若f x ()在区间103(,)上单调递增，求b 的取值范围函数的导数由①式2f x x bx b ()(=++2f x 2x b '()(=+22x b 12x x bx b )()()]=+--++23bx x 5()-==-⑥ 当f x ()在区间103(,)上单调递增时，则：f x 0'()>，即：1f x kx x 03'()()=--> ⑦若保证⑦式成立，对比⑥⑦式，则⑥式中：23b 153-≥ 即：69b 5-≥，即：9b 1≤，即：1b 9≤，故：1b 9(,]∈-∞ 本题答案：⑴ 极大值4，极小值0； ⑵ b 的取值范围 19(,]-∞.54、[江西19]如图，四棱锥P ABCD -中，ABCD 为矩形，平面PAD ⊥平面ABCD .⑴求证：AB PD ⊥；⑵若o BPC 90∠=，PB =PC 2=，问AB 为何值时，四棱锥P ABCD -的体积最大？并求此时平面PBC 与平面DPC 夹角的余弦值.[解析] ⑴求证：AB PD ⊥因为ABCD 为矩形，所以AB AD ⊥；又因为平面PAD ⊥平面ABCD ，AD 为两平面的交线，根据平面与平面垂直的性质定理：若两平面垂直，则在一个平面内垂直于交线的直PA BCD线垂直于另一个平面.故：AB PAD ⊥平面.根据直线与平面垂直的定义：若一直线与一平面垂直，则此直线与该平面内的任何直线垂直.故：AB PD ⊥. 证毕.⑵若o BPC 90∠=，PB =PC 2=，问AB 为何值时，四棱锥P ABCD -的体积最大？并求此时平面PBC 与平面DPC 夹角的余弦值.在Rt PBC ∆中，由勾股定理得：BC ==过P 作PE AD ⊥，交AD 于E ；过E 作EF BC ⊥，交BC 于F ；连结PF .由三垂线定理得：AD PEF ⊥平面，即：BC PEF ⊥平面. 设AB x =，则矩形ABCD， 由PBC 11S PB PC BC PF 22∆=⋅⋅=⋅⋅得：PB PC PF BC ⋅== 在Rt PEF ∆中，由勾股定理得：PE ==四棱锥P ABCD -的体积为：ABCD 111V S PE 333=⋅⋅=⋅= ① 由均值不等式：22a b ab 2+≤（当且仅当a b =时取等号）故：226x 86x 42()+-≤= ② 将②代入①式得：PABC DEF=时③式取等号，即体积V=则V最大时：226x86x=-，即：26x4=，即：22x3=，即：x=故：当AB=时，四棱锥P ABCD-的体积最大.⑶要求此时平面PBC与平面DPC夹角的余弦值.设111m(,,)αβγ=为过E点垂直于平面PBC的向量，设222n(,,)αβγ=为过E点垂直于平面DPC的向量.则：m FC⊥，m PC⊥④而：n DC⊥，n PD⊥⑤以E点为原点，以EF为x轴，以ED为y轴，以EP为z轴，建立三维直角坐标系.FC3===，PE3===则：E000(,,)，F00,)，C0)，D00()，P00(,则：FC003(,)=，6PC333(=-；6DC00(,)=，PD0(=.由④式m FC⊥得：111m FC000(,,)()αβγ⋅=⋅=，即：10β=；由④式mPC⊥得：111m PC0333(,,)αβγ⋅=⋅-=即：11120αβγ+-=，即：110αγ-=；令11α=，则11γ=，故：m101(,,)=⑥PA BCDEF由⑤式n PD ⊥得：222n PD 00(,,)(αβγ⋅=⋅-= 即：2220βγ-=，令：21β=，则：22γ=，故：n 012(,,)= 法向量m 和n 的点乘：2m nm n m n1cos ,⋅<>====最后一定画图，以此来决定法向量的夹角是二面角还是二面角的补角. 经画图确定，平面PBC 与平面DPC . 本题答案：⑵AB 3=；5. 55、[江西20] 如图，已知双曲线222x C y 1a :-= （a 0>）的右焦点F ,点A B ,分别在C 的两条渐近线上，AF x ⊥轴，AB OB ⊥，BF OA ∥ (O 为坐标原点). ⑴求双曲线C 的方程；⑵过C 上一点00P x y (,)（0y 0≠）的直线002x x l y y 1a:-=与直线AF 相交于点M ，与直线3x 2=相交于点N，证明点P 在C 上移动时，MF NF 恒为定值，并求此定值.[解析] ⑴求双曲线C 的方程实际上是求a . 双曲线C 的方程：222x y 1a -=，则右焦点F c 0(,)，其中c ==渐近线OA 方程：x y a =，A 点坐标：A x c =，A A x cy a a == 渐近线OB 方程：x y a =-，其斜率：OB 1k a=-因为AB OB ⊥，所以AB 的斜率：OB1k a k =-=故AB 的直线方程：A A y a x x y ()=-+ ① A> B 点在AB 直线上，故：B B A A y a x x y ()=-+ ②同时B 点在OB 直线上，故：BB x y a=-③ 联立②③得：B A A 1a x ax y a ()+=-，即：A A B 2a ax y x 1a()-=+ 代入③得：B A A B 2x ax y y a 1a ()-=-=-+ B> 由于BF OA ∥，即其斜率相等由于OA 1k a=；B F B BF B F B y y y k x x x c -==--，所以：A A 2B A A 2A A B A A 2ax y y ax y 11a a ax y a x c a ax y c 1a c 1a ()()()()---+===-----+-+ 即：2A A A A a ax y a ax y c 1a ()()()-=--++ 即：22A A 2a x ay c 1a ()()-=+ ④ 将A x c =，A cy a=代入上式得：222a c c c 1a ()()-=+ 即：222a 11a ()-=+，即：2a 3=故，双曲线C 的方程为：22x y 13-= ⑤而c 2===⑵ 过C 上一点00P x y (,)（0y 0≠）的直线00x xl y y 13:-=与直线AF 相交于点M ，与直线3x 2=相交于点N ，证明点P 在C 上移动时，MF NF 恒为定值，并求此定值.M 点的坐标为：M x c 2==，而0M0M x x y y 13-=得：00M 002x 12x 33y y 3y --==； N 点的坐标为：N 3x 2=，而0N 0N x x y y 13-=得：00N 00x 1x 22y y 2y --== F 点的坐标为：F x c 2==，F y 0=P 点的坐标满足C 的方程：2200x y 13-=，即：222000x x 3y 133-=-=故：002x 31MF 3y -===⋅ ⑥NF ========⑦由⑥和⑦得：1MF31NF3==本题答案：⑴ 22x y 13-=；⑵MF NF 3=. 56、[江西21]随机将122n ,,...,(n N *∈)这2n 个连续正整数分成A B ,两组，每组n 个数，A 组最小数为1a ，最大数为2a ；B 组最小数为1b ，最大数为2b ，记21a a ξ=-,21b b η=-⑴当n 3=时，求ξ的分布列和数学期望；⑵令C 表示事件ξ与η的取值恰好相等，求事件C 发生的概率P C ()；⑶对⑵中的事件C ,C 表示C 的对立事件，判断P C ()和P C ()的大小关系，并说明理由。

2014年福建省高考压轴卷理科综合能力测试物理部分第I 卷（ 必考）每小题6分，在下列各题的四个选项中，只有一个选项是正确的 13．位于原点的波源在t ＝0开始沿y 轴做简谐运动，它激起横波沿x 轴传播，当t ＝0.15s的图像如右图所示，此时波恰好传到P 点，则（ ）A.波长是0.4mB.该波源的频率是0.2HzC. P 点将向右运动D. P 点将向下运动解析：由图的波形图可读出λ=0.4m ，A 正确。

T=0.2s ，f=5Hz,B 错。

P 是向上运动，不迁移，CD 错。

14．两块完全相同的截面为等腰三角形的玻璃梭镜ABC 和A'B'C ’如图放置，AC与A'C ’间有均匀的未知透明介质，现有一细束单色光从图中O 点垂直于AB 面射入，从AB ’面射出，P 为入射光线所在直线与A ．B ，的交点，以下说法正确的是（C ） A ．出射点一定在P 点上方 B ．出射点一定在P 点下方 C ．出射光线一定与入射光线平行 D ．若光从P 点上方射出，则光在未知介质中传播较棱镜中的传播速度大解析：AC 与A'C ’间有均匀的未知透明介质，可看成类似“玻璃砖”，则：出射光线一定与入射光线平行，选C 。

未知透明介质的折射率大小如何未确定，A 、B 都未定。

若折射率大于玻璃的折射率，光从P 点上方射出，由n=c/v ，传播速度小，D 错。

15．下图为远距离输电的电路原理图，变压器均为理想变压器并标示了电压和电流，其中输电线总电阻为R ，则（ B ）A ．22U I R=B ．22UI R<C ．用户得到的电功率与电厂输出的电功率相等D ．用户得到的交变电流的频率小于电厂输出交变电流的频率解析：U 2=U 3+I 2R ，A 错，B 对。

有线路损耗。

C 错。

输电频率不变，D 错。

16．2013年12月2日1时30分，“嫦娥三号”月球探测器搭载长征三号乙火箭发射升空。

该卫星将在距月球表面高度为h 的轨道上做匀速圆周运动，其运行的周期为T ；最终在月球表面实现软着陆。

绝密★启用前 试卷类型：A山东省2014年高考仿真模拟冲刺卷（三）理科数学满分150分 考试用时120分钟参考公式：如果事件A ，B 互斥，那么P （A+B ）=P （A ）+P （B ）; 如果事件A ，B 独立，那么P （AB ）=P （A ）·P （B ）．如果事件A 在一次试验中发生的概率是p ，那么n 次独立重复试验中事件A 恰好发生k 次的概 率：).,,2,1,0()1()(n k p p C k P kn kkn n =-=-第Ⅰ卷（选择题 共50分）一、选择题：（本大题共10小题，每小题5分，共50分．每小题给出的四个选项中，只有一项是符合题目要求的）1．若复数2(1)ai +（i 为虚数单位）是纯虚数，则实数=a （ ）A ．1±B ．1-C ．0D ．1 2．下列有关命题的叙述错误的是（ ）A ．若p 且q 为假命题，则p ，q 均为假命题B ．若p ⌝是q 的必要条件，则p 是q ⌝的充分条件C ．命题“x x R x -∈∀2,≥0”的否定是“x x R x -∈∃2,＜0” D ．“x ＞2”是“211<x ”的充分不必要条件 3．设集合{}{}|31,,|5,,A x x k k N B x x x Q ==+∈=≤∈则B 等于（ ）A ．{1,2,5}B ．{l, 2，4, 5}C ．{1，4, 5}D ．{1，2，4}4．在样本的频率分布直方图中，一共有)3(≥m m 个小矩形，第3个小矩形的面积等于其余m-1个小矩形面积和的41，且样本容量为100，则第3组的频数是（ ）A ．10B ．25C ．20D ．405．如右图,在△ABC 中, 13AN NC =,P 是BN 上的一点,若29AP m AB AC −−→−−→−−→=+,则实数m 的值为 （ ）A ．19B ．31C ．1D ．36．已知()()()2,log 0,1x a f x a g x x a a -==>≠，若()()440f g ⋅-<，则y=()f x ，y=()g x 在同一坐标系内的大致图象是（ ）7．已知()f x 为R 上的可导函数，且,x R ∀∈均有/()()f x f x >，则有（ ）A ．20132013(2013)(0),(2013)(0)e f f f e f ->< B ．20132013(2013)(0),(2013)(0)e f f f e f -<< C ．20132013(2013)(0),(2013)(0)ef f f e f ->> D ．20132013(2013)(0),(2013)(0)ef f f e f -<>8．将函数x y 2sin =的图象向右平移4π个单位，再向上平移1个单位，所得函数图象对应的解析式为（ ）A ．1)42sin(+-=πx yB ．x y 2cos 2= C ．x y 2sin 2=D ．x y 2cos -=9．将A ，B ，C ，D ，E 五种不同的文件放入编号依次为1，2，3，4，5，6，7的七个抽屉内，每个抽屉至多放一种文件，若文件A 、B 必须放入相邻的抽屉内，文件C 、D 也必须放在相邻的抽屉内，则所有不同的放法有（ ） A ．192B ．144C ．288D ．24010．如果函数2()ln(1)a f x x b =-+的图象在1x =处的切线l 过点1(0,)b-，并且l 与圆C ：221x y +=相离，则点（a,b ）与圆C 的位置关系是（ ）A ．在圆上B ．在圆外C ．在圆内D ．不能确定第Ⅱ卷（非选择题 共100分）二、填空题：（本大题共5个小题，每小题5分，共25分．将答案填在题中横线上） 11．等差数列{a n }中，a 4+ a 10+ a 16=30，则a 18-2a 14的值为 ．12．设动点),(y x P 满足⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+00502402y x y x y x ，则y x z 25+=的最大值是 ．13．二项式（1+sinx ）n 的展开式中，末尾两项的系数之和为7，且系数最大的一项的值为25，则x 在[0，2π]内的值为 ． 14．直线l 过点(1,3)-，且与曲线12y x =-在点(1,1)-处的切线相互垂直，，则直线l 的方程为 ；15．下列结论中正确的是 ．① 函数y=f （x ）是定义在R 上的偶函数，且f （x+1）=- f （x ），则函数y=f （x ）的图像关于直线x=1对称；② 2~(16,),(17)0.35,(1516)0.15;N P P ξσξξ>=<<=已知若则 ③ ()(,),(,0]f x -∞+∞-∞已知是定义在上的偶函数且在上是增函数1.21(ln ),(log 3),(0.4),;43a fb fc f c a b -===<<设则④ 线性相关系数r 的绝对值越接近于1，表明两个变量线性相关程度越弱．三、解答题（本大题共6个小题，共75分．解答应写出文字说明，证明过程或演算步骤） 16．（本小题满分12分）设△ABC 的内角,,A B C 所对的边分别为,,a b c ,且6,2a c b +==,7cos 9B =. （Ⅰ）求,a c 的值; （Ⅱ）求sin()A B -的值.如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,BC AB ⊥,AB AS =,过A 作SB AF ⊥,垂足为F ,点G E ，分别是棱SC SA ，的中点.求证：（Ⅰ）平面//EFG 平面ABC ;（Ⅱ）SA BC ⊥.ABCSGFE一个盒子装有六张卡片，上面分别写着如下六个函数：31()f x x =,2()5xf x =,3()2f x =，421()21x x f x -=+，5()sin()2f x x π=+，6()cos f x x x =．（Ⅰ）从中任意拿取2张卡片，若其中有一张卡片上写着的函数为奇函数。

14年高考数学压轴题系列训练含答案及解析详解1．（本小题满分14分）如图，设抛物线的焦点为F，动点P在直线上运动，过P 作抛物线C的两条切线PA、PB，且与抛物线C分别相切于A、B两点.（1）求△APB的重心G的轨迹方程.（2）证明∠PFA=∠PFB.解：（1）设切点A、B坐标分别为，∴切线AP的方程为：切线BP的方程为：解得P点的坐标为：所以△APB的重心G的坐标为，所以，由点P在直线l上运动，从而得到重心G的轨迹方程为：（2）方法1：因为由于P点在抛物线外，则∴同理有∴∠AFP=∠PFB.方法2：①当所以P点坐标为，则P点到直线AF的距离为：即所以P点到直线BF的距离为：所以d1=d2，即得∠AFP=∠PFB.②当时，直线AF的方程：直线BF的方程：所以P点到直线AF的距离为：，同理可得到P点到直线BF的距离，因此由d1=d2，可得到∠AFP=∠PFB. 2．（本小题满分12分）设A、B是椭圆上的两点，点N（1，3）是线段AB的中点，线段AB的垂直平分线与椭圆相交于C、D两点.（Ⅰ）确定的取值范围，并求直线AB的方程；（Ⅱ）试判断是否存在这样的，使得A、B、C、D四点在同一个圆上？并说明理由.（此题不要求在答题卡上画图）本小题主要考查直线、圆和椭圆等平面解析几何的基础知识以及推理运算能力和综合解决问题的能力.（Ⅰ）解法1：依题意，可设直线AB的方程为，整理得①设是方程①的两个不同的根，∴②且由N（1，3）是线段AB的中点，得解得k=－1，代入②得，的取值范围是（12，+∞）.于是，直线AB的方程为解法2：设则有依题意，∵N（1，3）是AB的中点，∴又由N（1，3）在椭圆内，∴∴的取值范围是（12，+∞）.直线AB的方程为y－3=－（x－1），即x+y－4=0.（Ⅱ）解法1：∵CD垂直平分AB，∴直线CD的方程为y－3=x－1，即x－y+2=0，代入椭圆方程，整理得又设CD的中点为是方程③的两根，∴于是由弦长公式可得④将直线AB的方程x+y－4=0，代入椭圆方程得⑤同理可得⑥∵当时，假设存在>12，使得A、B、C、D四点共圆，则CD必为圆的直径，点M为圆心.点M到直线AB的距离为⑦于是，由④、⑥、⑦式和勾股定理可得故当>12时，A、B、C、D四点匀在以M为圆心，为半径的圆上.（注：上述解法中最后一步可按如下解法获得：）A、B、C、D共圆△ACD为直角三角形，A为直角|AN|2=|CN|·|DN|，即⑧由⑥式知，⑧式左边由④和⑦知，⑧式右边∴⑧式成立，即A、B、C、D四点共圆.解法2：由（Ⅱ）解法1及λ>12,∵CD垂直平分AB，∴直线CD方程为，代入椭圆方程，整理得③将直线AB的方程x+y－4=0，代入椭圆方程，整理得⑤解③和⑤式可得不妨设∴计算可得，∴A在以CD为直径的圆上.又B为A关于CD的对称点，∴A、B、C、D四点共圆.（注：也可用勾股定理证明AC⊥AD）3．（本小题满分14分）已知不等式为大于2的整数，表示不超过的最大整数. 设数列的各项为正，且满足（Ⅰ）证明（Ⅱ）猜测数列是否有极限？如果有，写出极限的值（不必证明）；（Ⅲ）试确定一个正整数N，使得当时，对任意b>0，都有本小题主要考查数列、极限及不等式的综合应用以及归纳递推的思想.（Ⅰ）证法1：∵当即于是有所有不等式两边相加可得由已知不等式知，当n≥3时有，∵证法2：设，首先利用数学归纳法证不等式（i）当n=3时，由知不等式成立.（ii）假设当n=k（k≥3）时，不等式成立，即则即当n=k+1时，不等式也成立.由（i）、（ii）知，又由已知不等式得（Ⅱ）有极限，且（Ⅲ）∵则有故取N=1024，可使当n>N时，都有4．如图，已知椭圆的中心在坐标原点，焦点F1，F2在x轴上，长轴A1A2的长为4，左准线l与x轴的交点为M，|MA1|∶|A1F1|＝2∶1．(Ⅰ)求椭圆的方程；(Ⅱ)若点P为l上的动点，求∠F1PF2最大值．本题主要考查椭圆的几何性质、椭圆方程、两条直线的夹角等基础知识，考查解析几何的基本思想方法和综合解题能力.满分14分.解：(Ⅰ)设椭圆方程为，半焦距为，则(Ⅱ)5．已知函数和的图象关于原点对称，且．(Ⅰ)求函数的解析式；(Ⅱ)解不等式；(Ⅲ)若在上是增函数，求实数的取值范围．本题主要考查函数图象的对称、二次函数的基本性质与不等式的应用等基础知识，以及综合运用所学知识分析和解决问题的能力.满分14分.解：(Ⅰ)设函数的图象上任意一点关于原点的对称点为，则∵点在函数的图象上∴(Ⅱ)由当时，，此时不等式无解.当时，，解得.因此，原不等式的解集为.（Ⅲ）①②ⅰ）ⅱ）6．(本题满分16分)本题共有3个小题,第1小题满分4分, 第2小题满分6分, 第3小题满分6分.对定义域分别是D f、D g的函数y=f(x) 、y=g(x),(1) 若函数f(x)=,g(x)=x2,x∈R,写出函数h(x)的解析式;(2) 求问题(1)中函数h(x)的值域;(3)若g(x)=f(x+α), 其中α是常数,且α∈[0,π],请设计一个定义域为R的函数y=f(x),及一个α的值,使得h(x)=cos4x,并予以证明.[解] (1)h(x)= x∈(-∞,1)∪(1,+∞)1 x=1(2) 当x≠1时, h(x)= =x-1++2,若x>1时, 则h(x)≥4,其中等号当x=2时成立若x<1时, 则h(x)≤ 0,其中等号当x=0时成立∴函数h(x)的值域是(-∞,0] {1}∪[4,+∞)(3)令f(x)=sin2x+cos2x,α=则g(x)=f(x+α)= sin2(x+)+cos2(x+)=cos2x-sin2x,于是h(x)= f(x)·f(x+α)= (sin2x+co2sx)( cos2x-sin2x)=cos4x.另解令f(x)=1+sin2x, α=,g(x)=f(x+α)= 1+sin2(x+π)=1-sin2x,于是h(x)= f(x)·f(x+α)= (1+sin2x)( 1-sin2x)=cos4x.7．(本题满分18分)本题共有3个小题,第1小题满分4分, 第2小题满分8分, 第3小题满分6分.在直角坐标平面中,已知点P1(1,2),P2(2,22),┄,P n(n,2n),其中n是正整数.对平面上任一点A0,记A1为A0关于点P1的对称点, A2为A1关于点P2的对称点, ┄, A N为A N-1关于点P N的对称点.(1)求向量的坐标;(2)当点A0在曲线C上移动时, 点A2的轨迹是函数y=f(x)的图象,其中f(x)是以3为周期的周期函数,且当x∈(0,3]时,f(x)=lgx.求以曲线C为图象的函数在(1,4]上的解析式;(3)对任意偶数n,用n表示向量的坐标.[解](1)设点A0(x,y), A0为P1关于点的对称点A0的坐标为(2-x,4-y),A1为P2关于点的对称点A2的坐标为(2+x,4+y),∴={2,4}.(2) ∵={2,4},∴f(x)的图象由曲线C向右平移2个单位,再向上平移4个单位得到.因此, 曲线C是函数y=g(x)的图象,其中g(x)是以3为周期的周期函数,且当x∈(-2,1]时,g(x)=lg(x+2)-4.于是,当x∈(1,4]时,g(x)=lg(x-1)-4.另解设点A0(x,y), A2(x2,y2),于是x2-x=2,y2-y=4,若3< x2≤6,则0< x2-3≤3,于是f(x2)=f(x2-3)=lg(x2-3).当1< x≤4时, 则3< x2≤6,y+4=lg(x-1).∴当x∈(1,4]时,g(x)=lg(x-1)-4.(3) =,由于,得=2()=2({1,2}+{1,23}+┄+{1,2n-1})=2{,}={n,}。

12014年北京市各区高三一模试题分类汇编 03立体几何 (理科1 (2014年东城一模理科2 (2014年西城一模理科如图, 设 P 为正四面体 A BCD -表面 (含棱上与顶点不重合的一点, 由点 P 到四个顶点的距离组成的集合记为 M , 如果集合 M 中有且只有 2个元素,那么符合条件的点 P 有( C(A 4个(B 6个(C 10个(D 14个3 (2014年西城一模理科已知一个正三棱柱的所有棱长均等于 2,它的俯视图是一个边长为 2的正三角形,那么它的侧(左视图面积的最小值是__4 (20145 (2014______6 (2014年朝阳一模理科如图,在四棱锥 S ABCD -中, SB ⊥底面 ABCD .底面ABCD 为梯形,AB AD ⊥, AB ∥ CD , 1, 3AB AD ==, 2CD =. 若点 E 是线段 AD 上的动点, 则满足 90SEC ∠=︒的点 E 的个数是 __2_7 (2014年丰台一模理科棱长为 2的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是(B (A 143(B 4 (C 103 (D 38 (2014年石景山一模理科右图是某个三棱锥的三视图,其中主视图是等边三角形,左视图是直角三角形,俯视图是等腰直角三角形,则该三棱锥的体积是(B A . 12 B . 3 C .4 D . 69 (2014年顺义一模理科一个几何体的三视图如图所示,则这个几何体的体积是_________1 正视图侧视图俯视图111 侧视图俯视图主视图1主视图左视图俯视图ADC. P 俯视图主视图侧视图210 (2014年延庆一模理科右图是一个几何体的三视图,则该几何体的体积是 (AA . 3B . 34C . 1D . 3211 (2014年东城一模理科12 (2014年西城一模理科如图,在四棱柱1111ABCD A BC D -中,底面 ABCD 和侧面 11BCC B 都是矩形, E 是 CD 的中点, 1D E CD ⊥, 22AB BC ==(Ⅰ求证:1⊥BC D E ; (Ⅱ求证:1B C // 平面 1BED ;(Ⅲ若平面 11BCC B 与平面 1BED 所成的锐二面角的大小为π3,求线段 1D E 的长度 . 13 (2014年海淀一模理科如图 1,在 Rt △ ABC 中,∠ACB =30°,∠ ABC =90°, D 为 AC 中点,AE BD ⊥于 E ,延长 AE 交 BC 于 F ,将∆ABD 沿 BD 折起,使平面 ABD ⊥平面BCD ,如图 2所示.(Ⅰ求证:AE ⊥平面 BCD ; (Ⅱ求二面角 A – DC – B 的余弦值.(Ⅲ在线段 AF 上是否存在点 M 使得 //EM 平面 ADC ?若存在,请指明点 M 的位置;若不存在,请说明理由.14 (2014年朝阳一模理科如图 , 四棱锥 P ABCD -的底面为正方形 , 侧面 PAD ⊥底面A B C D . PAD △为等腰直角三角形,且 PA AD ⊥. E , F 分别为底边 AB 和侧棱 PC 的中点.(Ⅰ求证:EF ∥平面 PAD ;(Ⅱ求证:EF ⊥平面 PCD ;(Ⅲ求二面角 E PD C --的余弦值.15 (2014年丰台一模理科如图,在棱长为 1的正方体 ABCD-A1B1C1D1中, 点 E 是棱 AB 上的动点 . (Ⅰ求证:DA1⊥ ED1 ;(Ⅱ若直线 DA1与平面 CED1成角为 45o ,求AEAB的值; (Ⅲ写出点 E 到直线 D1C 距离的最大值及此时点 E 的位置(结论不要求证明 .主视图侧(左视图俯视图3主视图左视图俯视图1E BCAD FA E BCDPF316 (2014年石景山一模理科如图, 正三棱柱111ABC A B C -的底面边长是 2,D 是AC 的中点.(Ⅰ求证:1B C ∥平面 1A BD ;(Ⅱ求二面角1A BD A --的大小;(Ⅲ在线段 1AA 上是否存在一点 E , 使得平面 11B C E ⊥平面 1A BD ,若存在, 求出 AE 的长;若不存在,说明理由.17 (2014年顺义一模理科如图在四棱锥 P ABCD -中,底面 ABCD 是菱形, 060BAD ∠=, 平面 PAD ⊥平面 ABCD , 2PA PD AD ===, Q 为 AD 的中点, M 是棱PC 上一点,且 13PM PC =. (Ⅰ求证:PQ ⊥平面 ABCD ; (Ⅱ证明:PA ∥平面 BMQ (Ⅲ求二面角 M BQ C --的度数 .18 (2014年延庆一模理科在四棱锥 ABCD P -中, ⊥PA 平面 ABCD , 底面ABCD 是正方形,且 2==AD PA , F E , 分别是棱 PC AD , 的中点. (Ⅰ求证://EF 平面PAB ; (Ⅱ求证:⊥EF 平面 PBC ; (Ⅲ求二面角 D PC E --的大小.2014年北京市各区高三一模试题汇编 --立体几何 (理科答案1. ;2. C ; 3.; 4. 96 ; 5. 13, ; 6. 2 ; 7. B ; 8. B ; 9. ; 10. A ;11. 吧A 1A 1B1CC DFDM Q A C412(Ⅰ证明:因为底面 ABCD 和侧面 11BCC B 是矩形, 所以 BC CD ⊥, 1BC CC ⊥,又因为 1=CDCC C ,所以 BC ⊥平面11DCC D , ……………… 2分因为 1D E ⊂平面 11DCC D , 所以1BC D E ⊥. ………… 4分(Ⅱ证明 :因为 1111//, BB DD BB DD =,所以四边形 11D DBB 是平行四边形 .连接 1DB 交 1D B 于点 F ,连接 EF , 则 F 为 1DB 的中点 . 在1∆B CD 中,因为 DE CE =, 1DF B F =,所以1//EF B C . …………… 6分又因为 1⊄B C 平面 1BED , ⊂EF 平面1BED ,所以 1//BC 平面1BED . ……… 8分 (Ⅲ解 :由(Ⅰ可知 1BC D E ⊥, 又因为1D E CD ⊥, BCCD C =,所以 1D E ⊥平面 A BCD . ……………… 9分设 G 为 AB 的中点,以 E 为原点, EG , EC , 1ED如图建立空间直角坐标系, 设 1D E a =,则 1(0,0,0, (1,1,0, (0,0,, E B D a C 设平面1BED 法向量为 (, , x y z =n ,因为1(1,1,0, (0,0, EB ED a ==,由 10,0,EB ED ⎧⋅=⎪⎨⋅=⎪⎩n n 得 0, 0.x y z +=⎧⎨=⎩令 1x =,得 (1,1,0 =-n . ………… 11分设平面 11BCC B 法向量为111(, , x y z =m ,因为1(1,0,0, (1,1, CB CB a ==,由 10, 0,CB CB ⎧⋅=⎪⎨⋅=⎪⎩m m得 11110, 0.x x y az =⎧⎨++=⎩令 11z =,得 (0,,1 a =-m . ………… 12分由平面 11BCC B 与平面 1BED 所成的锐二面角的大小为π3, 得||π|cos , |cos 3⋅<>===m n m n m n , …………… 13分解得1a =. ……………… 14分13(Ⅰ因为平面 ABD ⊥平面 BCD ,交线为 BD ,又在ABD ∆中, AE BD ⊥于 E , AE ⊂平面 ABD所以 AE ⊥平面 BCD . ———————————————— 3分 (Ⅱ由(Ⅰ结论AE ⊥平面 BCD 可得 AE EF ⊥. 由题意可知 EF BD ⊥,又 AE ⊥BD .如图, 以 E 为坐标原点, 分别以 , , EF ED EA 所在直线为 x 轴, y 轴,z 轴,建立空间直角坐标系 E xyz -—— 4分不妨设 2AB BD DC AD ====,则1BE ED ==. 由图 1条件计算得, AE =BC =BF =则 (0,0,0,(0,1,0,(0,1,0, 3E D B AF C -——————— 5分,0, (0,1, DC AD ==.由 AE ⊥平面 BCD 可知平面 DCB 的法向量为 EA . ——————— 6分设平面 ADC 的法向量为 (, , x y z =n ,则 0, 0. DC AD ⎧⋅=⎪⎨⋅=⎪⎩n n 即 0,0.y y +==⎪⎩令 1z =,则 1y x ==,所以 (11 =-n . —————————— 8分平面 DCB 的法向量为 EA 所以 cos , ||||EA EA EA ⋅<>==⋅n n n ,所以二面角 A DC B --————————————— 9分 (Ⅲ设AM AF λ=,其中[0,1]λ∈.由于 AF =, 所以AM AF λλ==,其中[0,1]λ∈———————————— 10分5所以,0,(13EM EA AM λ⎛=+=-⎝———————————— 11分由 0EM ⋅=n ,即 03λ=-(1-——— 12分解得3=(0,14λ∈. ———— 13分所以在线段 AF 上存在点M 使 EM ADC ∥平面 ,且34AM AF =. ———————— 14分 14(Ⅰ证明:取 PD 的中点 G ,连接 FG , AG .因为 F , G 分别是 PC , PD 的中点,所以 FG 是△ PCD 的中位线. 所以 FG ∥ CD , 且 12FG CD =.又因为 E 是 AB 的中点,且底面 ABCD 为正方形,所以 1122AE AB CD ==,且 AE ∥ CD .所以 AE ∥ FG ,且 AE FG =.所以四边形 AEFG 是平行四边形 . 所以 EF ∥ AG .又 EF ⊄平面 PAD , AG ⊂平面 PAD ,所以 EF 平面PAD . ………………… 4分 (Ⅱ证明 :因为平面 PAD ⊥平面 A B C D , PA AD ⊥,且平面 PAD I 平面 ABCD AD =,所以 PA ⊥平面 ABCD .所以 PA AB ⊥, PA AD ⊥. 又因为 ABCD 为正方形, 所以 AB AD ⊥,所以 , , AB AD AP 两两垂直.以点 A 为原点,分别以 , , AB AD AP 为 , , x y z 轴,建立空间直角坐标系(如图 .由题意易知 AB AD AP ==,设 2AB AD AP ===,则(0,0,0A , (2,0,0B , (2,2,0C , (0,2,0D , (0,0,2P , (1,0,0E , (1,1,1F .因为 (0,11EF =uu u r , , (022 PD =-u u u r , , , (200 CD =-uu u r , , , 且 (0,11(0,2,2 0EF PD ⋅=⋅-=u u u r u u u r, , (0,11(2,00 0EF CD ⋅=⋅-=u u u r u u u r, ,所以 EF PD ⊥, EF CD ⊥.又因为 PD , CD 相交于 D ,所以 EF ⊥平面PCD . …………… 9分(Ⅲ易得 (102 EP =-uu r , , , (0,22 PD =-u u u r, .设平面 EPD 的法向量为 (, , x y z =n ,则 0,0. EP PD ⎧⋅=⎪⎨⋅=⎪⎩uuruu u r n n 所以 20, 220. x z y z -+=⎧⎨-=⎩即 2, . x z y z =⎧⎨=⎩令 1z =,则 (2,1,1=n .由(Ⅱ可知平面 PCD 的法向量是 (0,11EF =uu u r, , 所以 cos , EFEF EF⋅〈〉===⋅uu u r uu u r n n n E PD C --的大小为锐角,所以二面角 E PD C --. ………… 14分 15. 解:以 D 为坐标原点,建立如图所示的坐标系,则D(0,0,0,A(1, 0, 0 , B(1,1,0, C(0,1,0,D1(0,1,2,A1(1,0,1,设E(1,m,0(0≤m≤ 1(Ⅰ证明:1(1,0,1 DA =, 1(1, ,1 ED m =-- 111(1 0( 110DA ED m ⋅=⨯-+⨯-+⨯=所以 DA1⊥ED1. ----4分 (Ⅱ设平面 CED1的一个法向量为 (, , v x y z =, 则100v C D v C E ⎧⋅=⎪⎨⋅=⎪⎩,而 1(0,1,1 CD =-, (1, 1,0 CE m =-所以 0, (1 0, y z x m y -+=⎧⎨+-=⎩取 z=1,得 y=1,x=1-m, 得(1,1,1 v m =-.因为直线 DA1与平面 CED1成角为 45o ,所以 1sin45|cos , |DA v ︒=<> 所以11||||||DA v DA v ⋅=⋅2=,解得 m=12.-----11分 (Ⅲ点 E 到直线 D1C E 在 A 点处 .------14分 16(Ⅰ证明:连结 1AB 交 1A B 于 M ,连结 1B C DM ,, 因为三棱柱 111ABC A B C -是正三棱柱, 所以四边形 11AA B B 是矩形,所以 M 为 1A B 的中点.因为 D 是 AC 的中点,MA1A1B1CBCD所以 MD 是三角形 AB1C 的中位线，…………………………2 分所以 MD ∥B1C ．…………………………3 分因为平面 A 1C ∥平面 A 1BD ， B 1C 平面 A 1BD ，所以 B 1BD ．……………4 分（Ⅱ）解：作于 O ，所以平面 ABB1 A 1，所以在正三棱柱中如图建立空间直角坐标系．因为， AA ， D 是 AC 的中点．，3 ，…………………12 分，，，解得，又，即所以存在点 E ，使得平面平面A ．…………………………14 分 1BD 且令，则， y1， 0 ，， 0， 0 ， C(0 ，，所以 A(1，0 …………5 分 0 3 ， A1 (1，3 ， z 所以 D( ， 0 ，，， 0， 1 2 3 2 3 2 3 ，， 3 ，0 ．设， y， z 是平面 A1BD 的法向量，，， 2 所以即，， D B1 y OA A1 令，则，， x 结 BD ， Q 底面 ABCD 是菱形，且，所以，， 2 3 是平面 A1BD 的一个法向量．……………6 分由题意可知 AA 0 是平面 ABD 的一个法向量，………7 分 1 ， 3 ，．………………8 分所以二面角A ．…………………………9 分的大小为 3 x， 0 ，则，3 ， 3 ，，，（Ⅲ）设 E (1，所以，设平面 B1C1E 的法向量， y1 ， z1 ，所以即是等边三角形，由（Ⅰ）平面以 Q 为坐标原点，QA, QB, QP 分别为 x 轴 y 轴 z 轴建立空间直角坐标系则 Q (0, 0, 0, A(1, 0, 0, B(0, 3, 0, P(0, 0, 3 .————10 分设平面 BMQ 的法向量为，，，，，，注意到 MN ∥ PA 6，解得是平面 BMQ 的一个法向量——12 分（Ⅰ）证明：设 G 是 PB 的中点，连接 AG, GF ∵ E , F 分别是 AD, PC 的中点，∴ GF // 1 1 BC ， AE // BC 2 2 ∴ GF // AE ，∴ AEFG 是平行四边形，∴ EF // AG ………………2 分∵平面平面 PAB ，∴EF // 平面PAB ………………3 分（Ⅱ）∵，∴PB ，………………4 分∵，∴，又∵，∴ BC 平面 PAB ，∴，………………6 分∵ PB 与 BC 相交，∴平面 PBC ，∴平面 PBC ．………………7 分（Ⅲ）以 AB, AD, AP 分别为 x 轴、 y 轴、 z 轴，建立空间直角坐标系，…8 分∵，∴ E (0,1,0 ， C (2,2,0 ， P(0,0,2 ， F (1,1,1 设 H 是 PD 的中点，连接 AH ∵平面PBC ，∴同理可证平面 PCD ，∴ AH 是平面 PCD 的法向量，(0,1,1 ………………9 分，设平面 PEC 的法向量，则∴令，则∴分．………………13 分∴| ∴二面角 E 的大小为分 7。

绝密★启用前 试卷类型：A2014年高考数学压轴卷22()x x -++第Ⅰ卷（选择题 共50分）一、选择题（本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的）1、定义集合运算：A ⊙B ={z ︳z =xy ,x ∈A ,y ∈B },设集合A ={—2013,0,2013},B ={ln a ,e a },则集合A ⊙B 的所有元素之和为 【 】 A. 2013 B. 0 C. —2013 D. ln2013+e 20132、奇函数f (x )在（0，+∞）上的解析式是f (x )= x (1—x )，则在（-∞，0）上，f (x )的函数解析式是【 】A. f (x )= —x (1—x )B. f (x )= x(1+x ) C. f (x )= —x (1+x ) D. f (x )= x (x —1) 3、若复数221z i i=++，其中i 是虚数单位，则复数z 的模为 【 】 A.2B.C. D. 24、设a ∈R ，则“a =1”是“直线l 1：ax +2y —1=0与直线l 2：x +（a +1）y +4=0平行的【 】A.充分不必要条件B.必要不充分条件 C. 充分必要条件 D. 既不充分不必要条件 5、若一个螺栓的底面是正六边形，它的主视图和俯视图如图所示，则它的体 积是 【 】 A ． B ． π C ．D ．6、为得到函数πcos 23y x ⎛⎫=+ ⎪⎝⎭的图像，只需将函数sin 2y x =的图像 【 】 A ．向左平移5π12个长度单位B ．向右平移5π12个长度单位C ．向左平移5π6个长度单位 D ．向右平移5π6个长度单位7、若程序框图如图所示,则该程序运行后输出k 的值是( ) A. 4 B. 5C. 6D. 7容器8、从某高中随机选取5名高三男生，其身高和体重的数据如下表所示：根据上表可得回归直线方程0.56y x a =+，据此模型预报身高为172 cm 的高三男生的体重为【 】A ． 70.09B ． 70.12C ． 70.55D ． 71.059、在棱长分别为1，2，3的长方体上随机选取两个相异顶点，若每个顶点被选 的概率相同，则选到两个顶点的距离大于3的概率为 【 】A.47 B.37 C.27 D.31410、设等差数列{}n a 满足：22222233363645sin cos cos cos sin sin 1sin()a a a a a a a a -+-=+，公差(1,0)d ∈-. 若当且仅当9n =时，数列{}n a 的前n 项和n S 取得最大值，则首项1a 的取值范围是 【 】 A. 74,63ππ⎛⎫ ⎪⎝⎭B. 43,32ππ⎛⎫⎪⎝⎭ C. 74,63ππ⎡⎤⎢⎥⎣⎦D.43,32ππ⎡⎤⎢⎥⎣⎦第Ⅱ卷（非选择题 共100分）二、填空题：（本大题共5小题，每小题5分，共25分．把答案值填在答题卡的相应位置） 11、给n 个自上而下相连的正方形着黑色或白色，当n≤4时，在所有不同的着色方案中，黑色正方形互不相邻的着色方案如图1所示，由此推断，当n=6时，黑色正方形互不相邻的着色方案共有____________种，至少有两个黑色正方形相邻的着色方案共有____________.(结果用数值表示) 12、设(5nx 的展开式的各项系数之和为M ，二项式系数之和为N ，若M —N=240，则展开式中3x 的系数为13、如图是一种加热水和食物的太阳灶，上面装有可旋转的抛物面形的反光镜，镜的轴截面是抛物线的一部分，盛水和食物的容器放在抛物线的焦点处，容器由若干 根等长的铁筋焊接在一起的架子支撑。