几何变换之一轴对称变换(生).

几何变换中的镜面对称与轴对称几何变换是数学中研究图形在平面或空间中变换的方式，其中镜面对称和轴对称是两种常见的变换方式。

本文将介绍镜面对称和轴对称的概念、性质以及它们在几何变换中的应用。

一、镜面对称镜面对称是指一个图形相对于一个镜面进行对称，对称后的图形和原图形相互重合。

镜面对称可以分为平面上的镜面对称和空间中的镜面对称。

1. 平面上的镜面对称平面上的镜面对称是指一个平面图形通过一个平面镜面进行对称。

镜面对称的性质如下：a) 对称轴：镜面对称的镜面是一个直线，称为对称轴。

对称轴将平面分为两个对称的部分。

b) 重合：镜面对称的图形和它的镜像图形重合。

c) 保角：镜面对称保持角度不变。

平面上的镜面对称常用于绘制对称图形，也是设计、美术等领域中常用的构图手法之一。

2. 空间中的镜面对称空间中的镜面对称是指一个空间图形通过一个平面镜面进行对称。

空间中的镜面对称具有与平面上的镜面对称类似的性质，同样有对称轴、重合和保角的特点。

空间中的镜面对称也常常用于艺术创作，如立体雕塑、建筑设计等领域。

二、轴对称轴对称是指一个图形相对于一条轴进行对称，对称后的图形和原图形相互重合。

轴对称是相对于一条线来进行对称的，可以分为平面上的轴对称和空间中的轴对称。

1. 平面上的轴对称平面上的轴对称是指一个平面图形相对于一条直线进行对称。

轴对称的性质如下：a) 对称轴：轴对称的轴是一条直线，称为对称轴。

对称轴将平面分为两个对称的部分。

b) 重合：轴对称的图形和它的轴对称图形重合。

c) 保角：轴对称保持角度不变。

平面上的轴对称经常出现在几何图形中，是数学中常用的概念之一。

2. 空间中的轴对称空间中的轴对称是指一个空间图形相对于一条直线进行对称。

空间中的轴对称具有与平面上的轴对称类似的性质，同样有对称轴、重合和保角的特点。

空间中的轴对称也常常出现在几何图形、三维模型等领域中。

三、镜面对称与轴对称的应用镜面对称和轴对称在几何变换中有着广泛的应用。

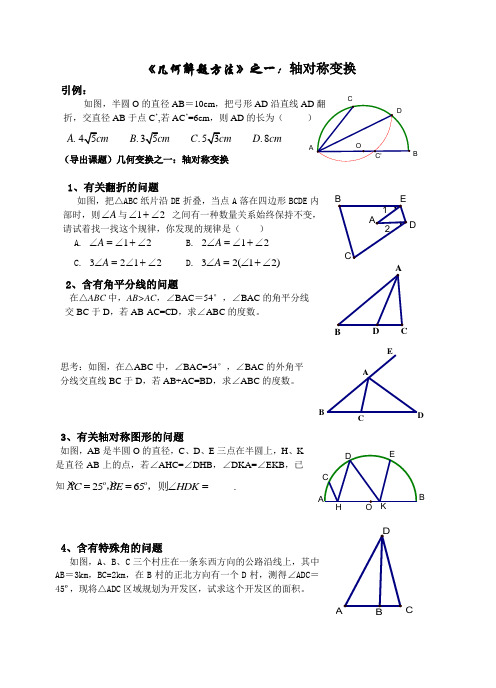
CBA《几何解题方法》之一：轴对称变换引例：如图，半圆O 的直径AB ＝10cm ，把弓形AD 沿直线AD 折，交直径AB 于点C ’,若AC ’=6cm ，则AD的长为（..8A B C D cm（导出课题）几何变换之一：轴对称变换1、有关翻折的问题如图，把△ABC 纸片沿DE 折叠，当点A 落在四边形BCDE 内部时，则∠A 与∠+∠12 之间有一种数量关系始终保持不变，请试着找一找这个规律，你发现的规律是（ ） A. ∠=∠+∠A 12 B. 212∠=∠+∠AC. 3212∠=∠+∠AD. )21(23∠+∠=∠A2、含有角平分线的问题在△ABC 中，AB>AC ，∠BAC ＝54°，∠BAC 的角平分线 交BC 于D ，若AB-AC=CD ，求∠ABC 的度数。

思考：如图，在△ABC 中，∠BAC=54°，∠BAC 的外角平分线交直线BC 于D ，若AB+AC=BD ，求∠ABC 的度数。

3、有关轴对称图形的问题如图，AB 是半圆O 的直径，C 、D 、E 三点在半圆上，H 、K 是直径AB 上的点，若∠AHC=∠DHB ，∠DKA=∠EKB ，已知2565____.AC BE HDK ==∠=，，则4、含有特殊角的问题如图，A 、B 、C 三个村庄在一条东西方向的公路沿线上，其中AB ＝3km ，BC=2km ，在B 村的正北方向有一个D 村，测得∠ADC ＝45º，现将△ADC 区域规划为开发区，试求这个开发区的面积。

E DCABCDB应用：1、如图，AD是△ABC的角平分线，BE⊥AD，交AD的延长线于E，•EF•∥AC交AB于F．求证：AF=FB．2、如图AB是半圆O的直径，点C在BA的延长线上运动（不与A重合），以OC为直径的半圆M与半圆O交于点D，∠DCB的平分线与半圆M交于点E。

（1）求证：CD是半圆O的切线；（2）过点E作EF⊥AB于F，则有OA=2EF,请说明理由。

几何变换之轴对称（翻折）翻折和折叠问题其实质就是对称问题，翻折图形的性质就是翻折前后图形是全等的，对应的边和角都是相等的。

以这个性质为基础，结合圆的性质，三角形相似，勾股定理设方程思想来考查。

那么碰到这类题型，我们的思路就要以翻折性质为基础，结合题中的条件，或利用三角形相似，或利用勾股定理设方程来解题！对于翻折和折叠题型分两个题型来讲，一类题型就是直接计算型，另一类是涉及到分类讨论型，由浅入深难度逐步加大，，掌握好分类讨论型的翻折问题，那么拿下中考数学翻折题型就没问题了！解决翻折题型的策略一：利用翻折的性质：①翻折前后两个图形全等。

对应边相等，对应角相等②对应点连线被对称轴垂直平分二：结合相关图形的性质（三角形，四边形等）三：运用勾股定理或者三角形相似建立方程。

翻折折叠题型（一），直接计算型，运用翻折的性质，结合题中的条件，或利用三角形相似，或利用勾股定理设方程来解题！一般难度小，我们要多做一些这些题型，熟练翻折的性质，以及常见的解题套路！翻折折叠题型（二），分类讨论型，运用翻的性质，结合题中的条件，或利用三角形相似，或利用勾股定理设方程来解题！般难度较大，需要综合运用题中的条件，多种情况讨论分析，需要准确的画图，才能准确分析！常见的几类类型1. 纸片中的折叠如图，有一条直的宽纸带，按照如图方式折叠，则＝.【解答】【解析】，如图所示：∵∠＝∠1，∠2＝∠1，∴∠＝∠2，∴2∠＋∠AEB＝180º，即2∠＋∠30º＝180º，解得∠＝75º.2. 三角形中的折叠在△ABC中，已知∠A=80°，∠C=30°，现把△CDE沿DE进行不同的折叠得△C’DE，对折叠后产生的夹角进行探究：（1）如图1，把△CDE沿DE折叠在四边形ADEB内，则求∠1+∠2的和；（2）如图2，把△CDE沿DE折叠覆盖∠A，则求∠1+∠2的和；（3）如图3，把△CDE沿DE斜向上折叠，探求∠1、∠2、∠C的关系.【解答】（1）∠1＋∠2＝60º；（2）∠1＋∠2＝50º；（3）∠2－∠1＝2∠C【解析】（1）由图可得∠1＋∠2＝180º－2∠CDE＋180º－2∠CED＝360º－2（∠CDE＋∠CED）＝360º－2（180º－∠C）＝2∠C＝60º（2）连接DG，如图所示：∠1＋∠2＝180º－∠C’－（∠ADG＋∠AGD）＝180º－30º－（180º－80º）＝50º（3）由图可得∠2－∠1＝180º－2∠CED－（2∠CDE－180º）＝360º－2（∠CDE＋∠CED）＝360º－2（180º－∠C）＝2∠C3. 矩形中的折叠如图，沿矩形ABCD的对角线BD折叠，点C落在点E的位置，已知BC＝8，AB＝6，求折叠后重合部分的面积.【解答】阴影部分的面积为【解析】∵点C与点E关于直线BD对称，∴∠1＝∠2，∵AD∥BC，∴∠1＝∠3，∴∠2＝∠3，∴FB＝FD，设，则，在Rt △BAF 中，，即，解得， ∴阴影部分面积. 4.圆中的折叠 如图，将半径为8的沿AB 折叠，弧AB 恰好经过与AB 垂直的半径OC 的中点D ，则折痕AB ＝ .【解答】AB = 【解析】延长CO 交AB 于E 点，连接OB ，如图所示：∵CE ⊥AB ，∴E 为AB 的中点，由题意可得CD=4，OD=4，OB=8，DE = 21(8×2 - 4) = 6，OE=6-4=2，在Rt △OEB 中，根据勾股定理可得：AB = .。

简单的几何变换几何变换是数学中的一个重要分支，它研究的是图形在平面或空间中的位置、形状和大小的变化。

在日常生活中，我们经常会遇到几何变换的应用，比如地图的缩放、图片的旋转和镜像等。

本文将从几何变换的基本概念开始，逐渐深入探讨几何变换的各种形式和应用。

1. 平移变换平移变换是最简单的几何变换之一，它将图形沿着某个方向移动一定的距离，而不改变其形状和大小。

平移变换可以用向量表示，假设有一个平面上的点P(x, y)，沿着向量v(a, b)进行平移，则点P'的坐标为P'(x+a, y+b)。

平移变换在计算机图形学中广泛应用，可以用来实现图形的移动、平移动画等效果。

2. 旋转变换旋转变换是将图形绕着某个点或轴进行旋转，使得图形相对于原来的位置发生旋转。

旋转变换可以用角度表示，假设有一个平面上的点P(x, y)，绕着原点逆时针旋转角度θ，则点P'的坐标为P'(x*cosθ - y*sinθ, x*sinθ + y*cosθ)。

旋转变换常用于计算机图形学、机器人学和物理学等领域，可以用来实现图形的旋转、物体的运动轨迹等模拟。

3. 缩放变换缩放变换是将图形按照一定比例进行放大或缩小，改变图形的大小而保持其形状不变。

缩放变换可以用比例因子表示，假设有一个平面上的点P(x, y)，按照比例因子s进行缩放，则点P'的坐标为P'(s*x, s*y)。

缩放变换在计算机图形学中常用于图像处理、图形的放大缩小等操作，也被广泛应用于地图的缩放和建筑物的设计等领域。

4. 对称变换对称变换是将图形关于某个直线、点或平面进行翻转，使得图形的两侧或两部分相互对称。

对称变换可以分为轴对称和中心对称两种形式。

轴对称变换是将图形关于某个直线进行翻转，使得图形的两侧镜像对称；中心对称变换是将图形关于某个点进行翻转，使得图形相对于该点对称。

对称变换在几何学和艺术设计中有着广泛的应用，可以用来构造对称的图案和装饰。

轴对称变换轴对称变换是一种常见的几何变换方式，它在我们的日常生活中无处不在。

无论是建筑设计、艺术创作，还是图形处理、物体制造，轴对称变换都扮演着重要角色。

本文将从不同领域的角度，分别介绍轴对称变换的应用。

在建筑设计中，轴对称变换常常被用于对称建筑的设计。

对称建筑体现了一种和谐、平衡的美感，它通过轴对称变换实现对称效果。

例如，古代的宫殿、寺庙和城堡等建筑物往往具有左右对称的结构。

通过轴对称变换，设计师可以在图纸上只绘制一半的建筑结构，然后通过轴对称变换复制另一半，从而节省了时间和精力。

在艺术创作中，轴对称变换也被广泛运用。

许多古代艺术作品，如中国的对联、剪纸和泥塑等，都采用了轴对称的构图方式。

这种构图方式通过轴对称变换使作品呈现出一种平衡、和谐的美感。

此外，现代艺术家也喜欢运用轴对称变换来创作独特的艺术作品。

他们通过将图像沿着某条轴进行镜像对称，创造出奇特、离奇的艺术效果，给人以强烈的视觉冲击力。

在图形处理中，轴对称变换是一种非常重要的操作。

图像处理软件通常都提供了轴对称变换的功能，使用户可以轻松地对图像进行镜像对称。

这对于修复照片中的缺陷、改善图像的美观度非常有帮助。

此外，轴对称变换还被广泛应用于计算机辅助设计（CAD）领域。

在CAD软件中，轴对称变换可以帮助工程师快速复制和对称设计图形，提高设计效率。

在物体制造中，轴对称变换也起到了重要的作用。

许多物体的制造过程都需要进行轴对称变换。

例如，汽车零部件、家电产品等的制造往往需要对称的设计。

通过轴对称变换，制造商可以在设计阶段更好地控制产品的对称性，提高产品的质量和可靠性。

此外，轴对称变换还广泛应用于机械加工工艺中。

在机械加工过程中，通过轴对称变换可以使物体在加工过程中保持平衡，从而提高加工精度和效率。

轴对称变换在建筑设计、艺术创作、图形处理和物体制造等领域都具有重要的应用价值。

它不仅能够帮助设计师和工程师提高工作效率，还能够为我们带来更美丽、更和谐的世界。

初中数学轴对称知识点初中数学轴对称知识点轴对称是初中数学中的一个重要部分，它是一种几何变换，在平面几何中经常使用。

轴对称就是将一个图形绕着某一直线对称，使得图形的两边完全重合的操作。

轴对称有许多应用，例如：制作对称的图案、设计对称的建筑和寻找自然界中的对称图案等。

掌握好轴对称的知识点，是初中数学的重要内容之一。

一、轴对称的定义轴对称是将平面中的一个图形绕着某一条直线对称，使得每个点关于这条直线对称。

二、轴对称图形的特点1. 轴对称图形的两侧完全相同，彼此对称。

2. 轴对称图形的中心轴是给定的直线，在给定的平面上不动。

3. 轴对称图形中排布的点与轴对称轴相固定，无论如何移动都不会移动到另一侧。

三、轴对称的性质1. 一条直线可以同时是多个图形的轴对称线，但一个图形只有一条轴对称线。

2. 轴对称的图形中任意两个点关于对称轴对称，即对称轴将图形分成两部分。

3. 对称轴上的点对图形的对称性质没有影响，对称轴与其他轴相同，没有特殊性。

4. 如果图形中有一个点在对称轴上，那么这个点还是在对称轴上，即对称轴与该点位置无关。

四、轴对称图形的种类1. 点对称：点对称就是当旋转一定角度时，每个点都对称于一个固定的中心点。

2. 直线对称：直线对称就是当沿一条相邻直线旋转一定角度时，整个图形都对称于这条直线。

3. 中心对称：中心对称就是当沿一个点旋转一定角度时，整个图形都对称于这个点。

五、轴对称的运用1. 寻找对称中心：将一图形旋转180°后，重叠的部分即为轴对称的中心。

2. 判断轴对称性：根据图形重叠的部分，判断是否对称。

3. 构造轴对称的图形：通过对称轴给出的点构造出轴对称的图形。

在初中数学中，轴对称是一个重要的几何概念。

掌握好轴对称的知识点，能帮助我们更好地理解平面几何知识，并在解题时更快捷的找到方法，提高解题效率。

同时，在实际生活中，轴对称也有一定的应用，例如：制作图案、设计建筑和寻找对称图案等。

我们应该认真学习并掌握这一重要内容。

轴对称变换在几何变换中的地位非常重要，较多的和全等三角形，相似三角形，勾股定理相结合.轴对称的性质：①.成轴对称的两个图形全等，即对应角相等，对应边相等；②对称轴是任何一对对应点所连线段的垂直平分线；③对应点的连线互相平行或在同一条直线上；1.抓住对称轴，找准对应点，根据关于某条直线对称的两个图形全等，确定图形中的边，角的相等关系；2.理解基本图形中的重要关系：如图，将矩形ABCD纸片沿EF折叠，点D的对称点是D′，点C的对称点是C′，则有①ED＝ED′，CD＝C′D′；②∠C＝∠C′，∠D＝∠D′，∠DEF＝∠D′EF；③等腰△GEF中，GE＝GF.3.求角的度数的问题，一般利用轴对称的性质，结合平行线的性质，三角形的内角和定理，相似三角形等知识来求解；4.求线段的长度的问题，或构造直角三角形，利用勾股定理列方程，或借助全等三角形，或利用相似三角形求解.例1.如图，将△ABC沿DE，DF翻折，顶点B，C均落在点G处，且BD与CD重合于线段DG，若∠A＝36°，∠AEG＋∠AFG的度数为（）．A .100°B .102°C .108°D .117°【答案】C例2.如图，对折矩形纸片ABCD ，使AD 与BC 重合，得到折痕EF ，把纸片展开.再一次折叠纸片，使点A 落在EF 上，得到折痕BM ，同时，得到线段BN ，若3AB，则BM 的长为（ ） N ABC D EF M A .332 B .2 C .3 D .23【答案】B例3.如图，在平行四边形ABCD 中，AB ＝6，BC ＝4，∠B ＝60°，点E 是边AB 上的一点，点F 是边CD 上一点，将平行四边形ABCD 沿EF 折叠，得到四边形EFGC ，点A 的对应点为点C ，点D 的对应点为点G ，则△CEF 的面积_____．73【精细解读】解：根据轴对称的性质可证△BCE ≌△GCF ，得到CE ＝CF 。

§22几何变换一、 平移变换1． 定义 设PQ 是一条给定的有向线段，T 是平面上的一个变换，它把平面图形F 上任一点X 变到'X ，使得PQ XX ='，则T 叫做沿有向线段PQ 的平移变换。

记为')(X X PQ T −−→−，图形')(F F PQ T −−→− 。

2． 主要性质 在平移变换下，对应线段平行且相等，直线变为直线，三角形变为三角形，圆变为圆。

两对应点连线段与给定的有向线段平行（共线）且相等。

二、 轴对称变换1． 定义 设l 是一条给定的直线，S 是平面上的一个变换，它把平面图形F 上任一点X 变到'X ，使得X 与'X 关于直线l 对称，则S 叫做以l 为对称轴的轴对称变换。

记为')(X X l S −−→−，图形')(F F l S −−→− 。

2． 主要性质 在轴对称变换下，对应线段相等，对应直线（段）或者平行，或者交于对称轴，且这两条直线的夹角被对称轴平分。

三、 旋转变换1． 定义 设α是一个定角，O 是一个定点，R 是平面上的一个变换，它把点O 仍变到O （不动点），而把平面图形F 上任一点X 变到'X ，使得OX OX ='，且α=∠'XOX ，则R 叫做绕中心O ，旋转角为α的旋转变换。

记为'),(X X O R −−→−α，图形'),(F F O R −−→−α 。

其中0<α时，表示'XOX ∠的始边OX 到终边X O '的旋转方向为顺时针方向；0>α时，为逆时针方向。

2． 主要性质 在旋转变换下，对应线段相等，对应直线的夹角等于旋转角。

四、 位似变换1． 定义 设O 是一个定点，H 是平面上的一个变换，它把平面图形F 上任一点X 变到'X ，使得k OX ⋅='，则H 叫做以O 为位似中心，k 为位似比的位似变换。