1、3矩形的性质

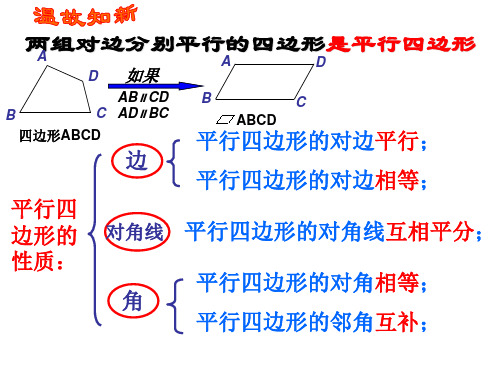
1.3 矩形的性质和判定【学习目标】： 1、学会识别矩形；2、掌握矩形的概念、判定和性质，会用矩形的性质和判定解决简单的问题；3、会运用矩形的知识解决有关问题, 重点：掌握矩形的性质，并学会应用 难点：理解矩形的特殊性 【知识梳理】1．矩形的定义：有一个角是直角的平行四边形叫做矩形． 2．矩形的性质矩形是特殊的平行四边形，它具有平行四边形的所有性质，•还具有自己独特的性质： ① 边的性质：对边平行且相等． ② 角的性质：四个角都是直角．③ 对角线性质：对角线互相平分且相等．④ 对称性：矩形是中心对称图形，也是轴对称图形． 直角三角形斜边上的中线等于斜边的一半． 直角三角形中，30︒角所对的边等于斜边的一半．点评：这两条直角三角形的性质在教材上是应用矩形的对角线推得，用三角形知识也可推得． 3．矩形的判定判定①：有一个角是直角的平行四边形是矩形． 判定②：对角线相等的平行四边形是矩形． 判定③：有三个角是直角的四边形是矩形． 【例题精讲】【矩形的判定】【例1】如图，在四边形ABCD 中，90ABC BCD ∠=∠=︒，AC BD =. 求证：四边形ABCD 是矩形．【例2】如图，已知在四边形ABCD 中，AC DB ⊥交于O ，E 、F 、G 、H 分别是四边的中点，求证四边形EFGH 是矩形．HG OFEDCBACDB A【例3】如图，在平行四边形ABCD 中，M 是AD 的中点，且MB MC =，求证：四边形ABCD 是矩形．【例4】设凸四边形ABCD 的4个顶点满足条件：每一点到其他3点的距离之和都要相等．试判断这个四边形是什么四边形?请证明你的结论。

【例5】如图，平行四边形ABCD 中，AQ 、BN 、CN 、DQ 分别是DAB ∠、ABC ∠、BCD ∠、CDA ∠的平分线，AQ 与BN 交于P ，CN 与DQ 交于M ，证明：四边形PQMN 是矩形．【例6】如图，在ABC ∆中，D 是BC 边上的一点，E 是AD 的中点，过A 点作BC 的平行线交CE 的延长线于点F ，且AF BD =，连结BF ． ⑴ 求证：BD CD =．⑵ 如果AB AC =，试判断四边形AFBD 的形状，并证明你的结论．【例7】已知，如图，在ABC ∆中，AB AC =，AD 是BC 边上的高，AF 是BAC ∠的外角平分线，DE ∥AB 交AF 于E ，试说明四边形ADCE 是矩形．FEDCBA321FE D CBAM CDB A NMQPDCBAEFDCAB ABCEFD【例8】如图所示，在Rt ABC ∆中，90ABC ∠=︒，将Rt ABC ∆绕点C 顺时针方向旋转60︒得到DEC ∆点E 在AC 上，再将Rt ABC ∆沿着AB 所在直线翻转180︒得到ABF ∆连接AD ． ⑴ 求证：四边形AFCD 是菱形；⑵ 连接BE 并延长交AD 于G 连接CG ，请问：四边形ABCG 是什么特殊平行四边形？为什么？【例9】 如图，在ABCD 中，AE BC ⊥于E ，AF CD ⊥于F ，AEF ∆的两条高相交于M ，20AC =，16EF =，求AM 的长．【例10】已知，如图矩形ABCD 中，延长CB 到E ，使CE AC =，F 是AE 中点． 求证：BF DF ⊥．【矩形的性质及应用】【例11】如图，在矩形ABCD 中，点E 是BC 上一点，AE AD =，DF AE ⊥，垂足为F .线段DF 与图中的哪一条线段相等？先将你猜想出的结论填写在下面的横线上，然后再加以证明。

矩形及特殊矩形知识点(经典完整版)
1. 矩形定义
矩形是一种具有四条相等长度的边且四个角都为直角的四边形。

2. 矩形的性质
- 矩形的对角线相等。

- 矩形的两条对边平行且相等。

- 矩形的四个角都为直角。

- 矩形的相邻两边互相垂直。

3. 特殊矩形
除了常见的矩形外，还有一些特殊类型的矩形，包括正方形、
长方形和黄金矩形。

3.1 正方形
正方形是一种特殊的矩形，它的四条边长度相等，且每个角都
为直角。

正方形具有以下性质：
- 任意一条边的长度可以表示为正方形的对角线长度的平方根
乘以√2。

- 正方形的对角线长度等于边长乘以√2。

3.2 长方形
长方形是一种具有不相等的长和宽的矩形，它的两对边分别平行且长度相等。

长方形具有以下性质：
- 长方形的对角线长度可以通过长和宽的值应用勾股定理来计算。

3.3 黄金矩形
黄金矩形是一种特殊的矩形，它的长和宽比例接近黄金分割比例。

黄金矩形具有以下性质：
- 黄金矩形的长和宽的比例可以接近黄金分割比例1:1.618。

- 黄金矩形的长和宽比例可以通过对角线长度的比例来计算。

4. 应用
矩形及其特殊类型的知识在几何学、工程学和建筑学中具有广泛的应用。

矩形可以用于设计建筑物的平面布局、计算房间面积、绘制电路图等。

以上是关于矩形及特殊矩形知识点的经典完整版介绍。

*注：以上内容为简要介绍，未涉及具体应用举例。

如需详细了解，请参考专业教材或专业指导。

*。

矩形中考要求知识点睛矩形的性质及判定1．矩形的定义：有一个角是直角的平行四边形叫做矩形．2．矩形的性质矩形是特殊的平行四边形，它具有平行四边形的所有性质，•还具有自己独特的性质：①边的性质：对边平行且相等．②角的性质：四个角都是直角．③对角线性质：对角线互相平分且相等．④对称性：矩形是中心对称图形，也是轴对称图形．直角三角形斜边上的中线等于斜边的一半．直角三角形中，30 角所对的边等于斜边的一半．点评：这两条直角三角形的性质在教材上是应用矩形的对角线推得，用三角形知识也可推得．3．矩形的判定判定①：有一个角是直角的平行四边形是矩形．判定②：对角线相等的平行四边形是矩形．判定③：有三个角是直角的四边形是矩形．例题精讲模块一矩形的概念【例1】矩形的定义：__________________的平行四边形叫做矩形．【答案】有一个角是直角；【例2】矩形的性质：矩形是一个特殊的平行四边形，它除了具有四边形和平行四边形所有的性质，还有：矩形的四个角______；矩形的对角线______；矩形是轴对称图形，它的对称轴是____________．【答案】都是直角，相等，经过对边中点的直线；【例3】矩形的判定：一个角是直角的______是矩形；对角线______的平行四边形是矩形；有______个角是直角的四边形是矩形．【答案】平行四边形；对角线相等；三个角【例4】矩形具有而平行四边形不具有的性质为（ ）A ．对角线相等B ．对角相等C ．对角线互相平分D ．对边相等【解析】省略 【答案】A【巩固】矩形ABCD 中，点H 为AD 的中点，P 为BC 上任意一点，PE HC ⊥交HC 于点E ，PF BH ⊥交BH 于点F ，当AB BC ，满足条件 时，四边形PEHF 是矩形 【解析】省略 【答案】2BC AB =模块二 矩形的性质【例5】如图，矩形ABCD 沿AE 折叠，使D 点落在BC 边上的F 点处，如果60BAF ∠=︒，则DAE ∠=FED CBA【解析】省略 【答案】15︒【例6】矩形ABCD 中，对角线AC 、BD 相交于O ，∠AOB ＝60°，AC ＝10cm ，则BC ＝______cm ，周长为 ．【答案】，【例7】如图，在矩形ABCD 中，,E F 分别是,BC AD 上的点，且BE DF =. 求证：ABE ∆≌CDF ∆.D EFCAB【解析】省略【答案】∵四边形ABCD 是矩形∴90AB AD B D =∠=∠=，. 在ABE ∆和CDF ∆中， 又∵BE DF =， ∴ABE ∆≌CDF ∆.【例8】如图，在矩形ABCD 中，点E 是BC 上一点，AE AD =，DF AE ⊥，垂足为F .线段DF 与图中的哪一条线段相等？先将你猜想出的结论填写在下面的横线上，然后再加以证明。

自学资料一、矩形及其性质【知识探索】1．有一个角是直角的平行四边形叫做矩形，也是长方形．2．矩形的性质：（1）矩形的四个角都是直角；（2）矩形的两条对角线相等．【说明】（1）矩形具有平行四边形的所有性质；（2）矩形既是中心对称图形，又是轴对称图形．对称中心是其对角线的交点，对称轴是每组对边的垂直平分线．【错题精练】例1．如图，已知矩形ABCD的对角线AC的长为10cm，连结矩形各边中点E、F、G、H得四边形EFGH，则四边形EFGH的周长为（）cm．第1页共7页自学七招之日计划护体神功：每日计划安排好，自学规划效率高非学科培训A. 20；B. ；C. ；D. 25．例2．已知：如图，矩形ABCD中，AC与BD交于O点，若点E是AO的中点，点F是OD的中点．求证：BE=CF．例3．如图，矩形ABCD中，延长AB至E，延长CD至F，BE=DF，连接EF，与BC、AD分别相交于P、Q两点．（1）求证：CP=AQ；（2）若BP=1，PQ=2，∠AEF=45°，求矩形ABCD的面积例4．如图，矩形ABCD中，已知AB=6，BC=8，BD的垂直平分线交AD于点E，交BC于点F，则△BOF的面积为__________ ．第2页共7页自学七招之智慧树神拳：知识内容体系化，思维导图来助力非学科培训【举一反三】1．如图，在矩形ABCD中，点E在BC上，AE=AD，DF⊥AE于F，连接DE．证明：DF=DC2．如图，矩形ABCD中，AB=4，AD=3，M是边CD上一点，将△ADM沿直线AM对折，得到△ANM．（1）当AN平分∠MAB时，求DM的长；（2）连接BN，当DM=1时，求△ABN的面积；（3）当射线BN交线段CD于点F时，求DF的最大值．3．如图，AC为矩形ABCD的对角线，将边AB沿AE折叠，使点B落在AC上的点M处，将边CD沿CF折叠，使点D落在AC上的点N处．（1）求证：四边形AECF是平行四边形；（2）若AB=6，AC=10，求四边形AECF的面积．4．如图，矩形ABCD的对角线AC的中点为O，过点O作OE⊥BC于点E，连接OD，已知AB=6，BC=8，则四边形OECD的周长为__________ ．第3页共7页自学七招之以背代诵掌：高效记忆有妙招，以背代诵效果好非学科培训5．如图，在矩形ABCD中，对角线AC与BD相交于点O，过点A作AE⊥BD，垂足为点E，若∠EAC=2∠CAD，则∠BAE=__________ 度二、矩形的判定【知识探索】1．矩形的判定：（1）对角线相等的平行四边形是矩形．（2）有三个角是直角的四边形是矩形．【错题精练】例1．如图，在▱ABCD中，点O是边BC的中点，连接DO并延长，交AB延长线与点E，连接BD，EC．（1）求证：四边形BECD是平行四边形；（2）若∠A=50∘，则当∠BOD=°时，四边形BECD是矩形．例2．已知：如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交与BE的延长线于点F，且AF=DC，连接CF．（1）求证：D是BC的中点；（2）当AB与AC有何数量关系时，四边形ADCF为矩形，请说明理由．第4页共7页自学七招之智慧树神拳：知识内容体系化，思维导图来助力非学科培训【举一反三】1．已知，如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交与BE的延长线于点F，且AF=DC，连结CF．（1）求证：四边形ADCF是平行四边形；（2）当AB与AC有何数量关系时，四边形ADCF为矩形，请说明理由．2．已知：如图，AB=AC，AE=AF，且∠EAB=∠FAC，EF=BC．求证：四边形EBCF是矩形．1．已知：如图，在矩形ABCD中，点E在边AB上，点F在边BC上，且BE=CF，EF⊥DF，求证：BF=CD．2．如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE=DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（）第5页共7页自学七招之以背代诵掌：高效记忆有妙招，以背代诵效果好非学科培训A. △AFD≌△DCEB. AF=ADC. AB=AFD. BE=AD﹣DF3．如图，在平行四边形ABCD中，AB≠BC，连接AC，AE是∠BAD的平分线，交边DC的延长线于点F．（1）证明：CE=CF；（2）若∠B=60°，BC=2AB，试判断四边形ABFC的形状，并说明理由．（如图2所示）4．如图，在直线MN上和直线MN外分别取点A、B，过线段AB的中点作CD平行于MN，分别与∠MAB与∠NAB的平分线相交于点C、D．求证：四边形ACBD是矩形．5．如图，在▱ABCD中，E是DC边的中点，且EA=EB．求证：▱ABCD是矩形．6．下列说法中，错误的是（）第6页共7页自学七招之智慧树神拳：知识内容体系化，思维导图来助力非学科培训A. 平行四边形的对角线互相平分B. 对角线互相平分的四边形是平行四边形C. 菱形的对角线互相垂直D. 对角线互相垂直的四边形是菱形第7页共7页自学七招之以背代诵掌：高效记忆有妙招，以背代诵效果好非学科培训。

矩形的认识与分类矩形是几何学中常见的形状之一，具有许多重要的性质和用途。

本文将对矩形的基本定义、特点以及不同类型的矩形进行详细介绍。

一、基本定义矩形是一种有四个直角的四边形，其对边长度相等且相对平行。

也就是说，一条边和和其相邻的两条边构成一个直角。

二、性质和特点1. 对角线相等：矩形的对角线相等，而且相互平分。

2. 相对边平行：矩形的相对边是平行的。

3. 内角和为180度：矩形的内角和等于180度，每个角都是直角。

根据以上性质和特点，我们可以通过测量边长和角度来判断是否是矩形。

三、不同类型的矩形1. 正矩形：正矩形是一种特殊的矩形，其四个内角都是直角，并且所有边长相等。

正矩形常见于建筑物中的窗户、门框等。

2. 长方形：长方形也是一种矩形，其相邻两条边长度不同，但仍然保持直角。

长方形在日常生活中非常常见，例如书、手机、电视等。

3. 菱形：菱形是矩形的一种特殊情况，其对边长度相等，但相邻两边不平行。

菱形在宝石、纹身等领域中常见。

四、矩形的应用矩形在日常生活和工作中有着广泛的应用。

以下是一些常见的应用场景：1. 建筑设计：矩形常用于建筑设计中的墙壁、门窗等构造物的规划和设计。

2. 统计学：矩形常用于绘制柱状图，用于表示数据的分布情况和比较。

3. 地理学：地理学中常用矩形来表示地图上的区域。

总结：矩形是一种重要的几何形状，具有许多独特的性质和特点。

我们可以通过测量边长和角度来判断是否是矩形，并进一步分类为正矩形、长方形和菱形。

矩形在我们的日常生活和工作中有着广泛的应用，需要我们对其进行深入的认识和理解。

注：以上内容为文章的主要部分，字数仅为500字，如需增加字数可适当拓展各小节的内容，提供更多实际应用和相关案例。