2017年高考(270)云南昆明一中2017届高三第三次双基检测

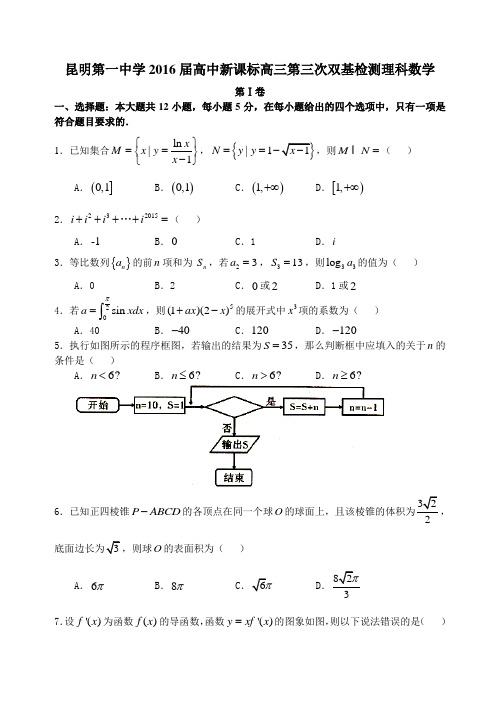
昆明第一中学2016届高中新课标高三第三次双基检测理科数学第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合ln |1x M x y x ⎧⎫==⎨⎬-⎩⎭，{|1N y y ==，则M N = （ ） A ．(]0,1B ．()0,1C ．()1,+∞D ．[)1,+∞2．232015i i i i++++=…（ ）A ．-1B ．0C ．1D ．i3．等比数列{}n a 的前n 项和为 n S ，若23a =，313S =，则33log a 的值为（ ）A ．0B ．2C ．0或2D ．1或24．若20sin a xdx π=⎰，则5(1)(2)ax x +-的展开式中3x 项的系数为（ ）A ．40B ．40-C ．120D ．120-5．执行如图所示的程序框图，若输出的结果为35S =，那么判断框中应填入的关于n 的条件是（ ）A ．6?n <B ．6?n ≤C ．6?n >D ．6?n ≥6．已知正四棱锥P ABCD -的各顶点在同一个球O ，O 的表面积为（ ）A ．6πB ．8πCD 7．设'()f x 为函数()f x 的导函数，函数'()y xf x =的图象如图，则以下说法错误的是（ ）A ．'(2)'(2)f f =-B ．当2x =-时，函数()f x 取得极小值C ．当2x =时，函数()f x 取得极大值D ．方程'()0xf x =与()0f x =均有3个实根8．已知变量x ，y 满足约束条件20,,,x y y x y x a -≥⎧⎪≥⎨⎪≥-+⎩且2z x y =+的最小值为4，则实数a 的值为（ ）A ．1B ．52C ．83D ．9．某四面体的三视图如图所示，正视图、侧视图、俯视图都是边长为2的正方形，则此四面体的体积是（ ）A ．23B ．43C ．83D ．810．设3log 4a =，4log 3b =，3log 2c =，则（ ）A ．a c b >>B ．a b c >>C ．b c a >>D ．c a b >>11．已知抛物线E ：22y x =的焦点为F ，E 上有四点A ，B ，C ，D 满足0FA FB FC FD +++= ，则||||||||FA FB FC FD +++= （ ）A ．4B ．3C ．2D ．112．在Rt △ABC中，AB AC ==M 为BC 的中点，动点P 满足3PM =，则△ABP 与△ACP 的面积之比的最大值为（ ）A ．7B ．8C ．9D ．10第Ⅱ卷二、填空题：本大题共4小题，每小题5分．13．在△ABC 中，||||AB AC AB AC +=- ，||2AB = ，||1AC =，D ，E 为线段BC的两个三等分点，则AD AE ⋅=．14．已知函数1()cos()12f x x ωϕ=++（0ω>），若()112f π=，1()42f π=，则ω的最小值为 ．15.从正方体的8个顶点中任取3个点，则以这3个点为顶点能构成正三角形的概率为 ．16．数列{}n a 的前n 项和为n S ，已知18a =，42a =，且212n n n a a a ++=-（*n N ∈），若n S 的最大值为a ，n nS 的最大值为b ，则a b += ．三、解答题：解答应写出文字说明，证明过程或演算步骤． 17．（本小题满分12分）在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且222c o s c o s 3s i n s i n1c o sA C A CB +=+． （1）求B ；（2）设函数2()cos cos f x x x x =-（x R ∈），求()f A 的取值范围．18．（本小题满分12分）某工厂在2010年至2014年每年的机器维修费用y （单位：千元）的数据如下表： 年份 2010 2011 2012 2013 2014 年份代号t 1 2 3 4 5 维修费用y 1.8 2.2 2.72.83.5（1）求y 关于t 的线性回归方程；（2）利用（1）中的回归方程，分析该厂在2010年至2014年每年的机器维修费用的变化情况，并预测该厂在2016年所需的机器维修费用．附：回归直线的斜率和截距的最小二乘估计公式分别为121()()()nii i nii tt y y btt ==--=-∑∑ ， ay bt =-19．（本小题满分12分）如图，三棱柱111ABC A B C -中，A C B C =，1AB AA =，1120ABB ∠=︒．（1）证明：1AB AC ⊥； （2）若平面11A ABB ⊥平面ABC，AB =，AC =111A CC B --的余弦值．20.（本小题满分12分）已知点P 为圆226x y +=上一动点，过点P 作x 轴的垂线，垂足为Q ，点M 满足(12PM PQ =- ．（1）求点M 的轨迹E 的方程；（2）过点(0,2)D -的直线l 与E 交于A ，B 两点，若以线段AB 为直径的圆N 过坐标原点O ，求圆N 的方程． 21．（本小题满分12分）已知函数()ln()x f x ke x m =-+．（1）若1k m ==，求函数()f x 的极小值； （2）当3k =，3m ≤时，证明：()ln 31f x >-．请考生在第22、23、24题中任选一题作答，如果多做，则按所做的第一题计分．作答时请写清题号． 22．（本小题满分10分）选修4—1：几何证明选讲如图，AB 是圆O 的直径，AC 是弦，直线EF 和圆O 相切于点C ，AD ⊥EF ，垂足为D ，直线EF 交BA 的延长线于点F ．（1）求证：∠BAC =∠DAC ； （2）若2OB =，1AD =，求证：BC AFBF BC=． 23．（本小题满分10分）选修4—4：坐标系与参数方程在平面直角坐标系xOy 中，直线l 的参数方程为3,4x m s y s =+⎧⎨=⎩（s 为参数），在以O 为极点，x 轴的非负半轴为极轴的极坐标系中，曲线C 的极坐标方程为cos 24cos ρρθθ=+．（1）求直线l 与曲线C 的普通方程；P（2）设直线l 与x 轴交于点P ，且于曲线C 相交于A ，B 两点，若||AB 是||PA 与||PB 的等比中项，求实数m 的值． 24．（本小题满分10分）选修4—5：不等式选讲已知函数()|2|f x x a =+，a R ∈．（1）当1a =-时，求不等式()|1|30f x x ++-≤的解集； （2）若对[]1,2x ∀∈，2()1f x x <+恒成立，求a 的取值范围．昆明市第一中学2016届高三考试参考答案（理科数学）一、选择题BACACBDDCBDA1. 解析：集合|0{M x x =>且1}x ≠，{}|1N y y =≤，所以{}|01M N x x =<<I ，选B ．2. 解析：因为()1230i i i i k k k k k ++++++=∈Z ，所以232015231i i i i i i i +⋅⋅⋅=+++-=++，选A ．3. 解析：因为23a =，313S =，联立化为231030q q -+=，解得13q =或3q =；当13q =时，31a =，33log 0a =，当3q =时，39a =，33log 2a =，选C ．4. 解析：由题意，2200sin (cos )1a xdx x ππ==-=⎰，则5(2)x -展开式中含2x 与3x 的项为232235280T C x x ==，323345240T C x x =-=-，所以5(1)(2)x x +-展开式中3x 项的系数为804040-=，选A.5. 解析：第一次循环，11S =，9n =；第二次循环20S =，8n =；第三次循环，28S =，7n =；第四次循环，35S =，6n =，结束循环，输出35S =，因此n 选C .6. 解析：如图，设点M 为正四棱锥P ABCD -的底面的中心，则PM为四棱锥的高，球心O 必在直线PM 上， 不妨设点O 在线段PM 上，球O 的半径为R ，连接OA ，则OA R =；由条件知13PM =，所以PM =，则2OM R =-，又由条件可求得2AM =，在Rt AOM ∆中，由勾股定理得222)R R =-+得R =O 在线段PM 的延长线上时 求得同样结果，故球O的表面积为248ππ=，选B ． 7. 解析：函数()f x 在(,2)-∞-单调递减，(2,2)-单调递增，(2,)+∞单调递减，所以(2)(2)0f f ''=-=，当2x =-时，函数取得极小值，当2x= 时，函数取得极大值，其图像可如图，所以D 错误，选D ．8. 解析：画出可行域（如图阴影部分所示）和直线0l ：20x y +=，观察图形，知直线2x y z +=过直线y x a =-+和20x y -=的交点2,33a a A ⎛⎫⎪⎝⎭时，z 取得最小值，即22433a a ⨯+=，解得3a =，选D.9. 解析：由于正视图、侧视图、俯视图都是边长为2的正方形，所以此四面体一定可以放在正方体中，所以可以在正方体中寻找四面体，如图所示，四面体ABCD 满足题意，所以此四面体的体积是11884222323-⨯⨯⨯⨯⨯=，选C. 10. 解析：3log 41a b =>>，令()l o g(x f x x =-，()ln(1)log (1)ln x x f x x x-=-=， ()21[ln (1)ln(1)]0(1)ln f x x x x x x x x'=--->-，()f x 在(1,)+∞单调递增，所以()()43f f >，即b c >，所以a b c >>，选B ．11. 解析：设11(,)A x y ，22(,)B x y ，33(,)C x y ，44(,)D x y ，由+++=0FA FB FC FD得12341111+++=08888y y y y ----，12341+++=2y y y y ，根据抛物线定义有+++=FA FB FC FD12341111+++++++=18888y y y y ，选D ．12. 解析：由1sin sin 2==1sin sin 2ABP ACP AB AP BAPS BAPS CAPAC AP CAP ∆∆⋅⋅⋅∠∠∠⋅⋅⋅∠可知要ABP ∆与ACP ∆的面积之比最大，只需BAP ∠最大，CAP ∠最小，所以当AP 与以M 为圆心，半径为3的圆相切时BAP ∠最大.因为3sin =5MAP ∠，4cos =5MAP ∠，所以ABP ∆与ACP ∆的面积之比的最大值为sin (45+)sin (45)MAP MAP ︒︒∠-∠cos +sin ==7cos sin MAP MAP MAP MAP∠∠∠-∠，选A ． 二、填空题13．10914．315．1716．128 13. 解析：由AB AC AB AC +=-，化简得0AB AC ⋅= ，所以AB AC ⊥，所以ABC ∆为直角三角形. 如图，以AB 所在直线为x轴，以AC 所在直线为y 轴建立平面直角坐标系，则()0,0A ，()2,0B ，()0,1C .由D ，E 为线段BC 的两个三等分点知41,33D ⎛⎫ ⎪⎝⎭，22,33E ⎛⎫⎪⎝⎭，41,33AD ⎛⎫= ⎪⎝⎭ ，22,33AE ⎛⎫= ⎪⎝⎭ ，所以AD AE ⋅= 42121033339⨯+⨯=.14. 解析：由题意可知函数12()cos()1(0)f x x ωϕω=++>的图象的一个对称中心为点,112π⎛⎫⎪⎝⎭，一条对称轴为直线4x π=，所以4412T ππ≤-，即232ππω≤，得3ω≥，所以ω的最小值为3．15. 解析：从正方体的8个顶点中任取3个点有38C 种取法，能构成正三角形的有11ABC ∆，11A DC ∆，11AB D ∆，11CB D ∆，1AB C ∆，1ADC ∆，1ABD ∆，1C BD ∆共8种可能，则所求的概率为81567P ==.16. 解析：因为212()n n n a a a n ++=-∈*N ，所以数列{}n a 为等差数列，由18a =，42a =得2d =-，所以22(1)9818(2)9=224n n n S n n n n -⎛⎫=+-=-+--+ ⎪⎝⎭，可知n S 的最大值20a =； 329n nS n n =-+，由()2318=0n n S n n '=-+，得6n =，可知n nS 的最大值108b =； 所以128a b +=. 三、解答题17．解：（1）由222cos cos sin 1cos A C A C B +=+，得2221sin 1sin sin 2sin A C A C B -+-=-，由正弦定理得：222a cb +-=，于是222cos 2a c b B ac +-==， 所以56B π=． （2）因2()cos cos f x x x x =-cos2122x x +=-1sin(2)62x π=--， 所以1()sin(2)62f A A π=--． 又因为ABC ∆中，56B π=，所以06A π<<，所以2666A πππ-<-<，所以11sin(2)262A π-<-<，即1()0f A -<<，C 1A A1DABCA 1C 1B 1所以()f A 的取值范围是()1,0-． 18．解：（1）由所给数据计算可得1(12345)35t =++++=， 1(1.8 2.2 2.7 2.8 3.5) 2.65y =++++=，521()4101410i i t t =-=++++=∑，51()()(2)(0.8)(1)(0.4)0(0.1)10.220.94iii t t y y =--=-⨯-+-⨯-+⨯-+⨯+⨯=∑，则51521()()40.410()ii i ii tt y y bt t ==--===-∑∑ ， ay bt =- 2.60.43 1.4=-⨯=， 则回归直线方程为 0.4 1.4y t =+．（2）由（1）知，0.40b=> ，故从2010年至2014年每年的机器维修费用在逐年增加，平均每年增加0.4千元，将2016年的年份代号记为7t =，代入（1）中的回归方程得ˆ0.47 1.4 4.2y =⨯+=（千元），故预测该厂在2016年所需的机器维修费用为4.2千元. ……… 12分 17. 解：（Ⅰ）证明：取AB 的中点D ，连接CD ，1A D ，因为1120ABB ∠= ，所以160A AB ∠= ，又1AB AA=， 所以1A AB ∆为正三角形，则11A A A B =，得1AB A D ⊥； 又因为AC BC =，所以AB CD ⊥，因为1A D CD D = ，所以AB ⊥平面1A DC ， 因为1AC ⊂平面1A DC ，所以1AB AC ⊥． （Ⅱ）由（Ⅰ）知1A D AB ⊥，AB CD ⊥，因为平面11A ABB ⊥平面ABC ，交线为AB ， 所以1AD ⊥平面ABC ，则1A D CD ⊥．以D 为原点，分别以DB ，DC ，1DA 所在直线为x ，y ，z 轴建立空间直角坐标系D xyz -，因为AB =AC =，由（Ⅰ）知11AA A B AB ===， 所以13A D =，CD ；所以(0,0,0)D，(A，B ，1(0,0,3)A，C ，得11CC AA ==，1(0,CA =，(BC =；设(,,)m x y z = 为平面11ACC 的法向量，由1m CC ⊥ ，1m CA ⊥可求得()m =； 设(,,)n x y z = 为平面1BCC的法向量，同理可求得(n =；由cos ,m nm n m n⋅<>=⨯17==， 所以二面角111A CC B --的余弦值为17．18. 解：（Ⅰ）设00(,)P x y ，0(,0)Q x ，(,)M x y，由=1PM PQ ⎛- ⎝⎭得000(,)=1(0,)x x y y y ⎛--- ⎝，0=x x，00=1y y y ⎫-⎪⎪⎭，所以0=x x，0y ，代人220+=6x y 得22+2=6x y ，22+=163x y ．（Ⅱ）设11(,)A x y ，22(,)B x y ，根据题意直线l 的斜率存在，设直线l 的方程为=2y kx -，由方程组22=2+2=6y kx x y -⎧⎨⎩消去y ，整理得22(2+1)8+2=0k x kx -，1228+=2+1k x x k ，1222=2+1x x k ，所以121224+=(+)4=2+1y y k x x k --，21212246=(2)(2)=2+1k y y kx kx k ---. ………8分 设点(,)C x y 为圆N 上任意一点，由=0AC BC ⋅得1122(,)(,)=0x x y y x x y y --⋅--，1212()()+()()=0x x x x y y y y ----，2212121212(+)++(+)+=0x x x x x x y y y y y y --，因为圆N 过坐标原点O ，所以1212+=0x x y y ，222246+=02+12+1k k k -，解得=1k ±， ………10分所以圆N的方程为2284++=033x x y y -或2284+++=033x x y y . ………12分19. 解：（Ⅰ）()ln(1)xf x e x =-+，所以()11x f x e x '=-+，……1分观察得()01001f e '=-=且()11xf x e x '=-+在(1,)-+∞上单调递增，所以当(1,0)x ∈-时()0f x '<，当(0,)x ∈+∞时()0f x '>，所以()f x 在(1,0)x ∈-单调递减，()f x 在(0,)x ∈+∞单调递增，故()f x 有极小值()01f =.……5分证明：（Ⅱ）因为3k m =≥，所以()3ln()3ln(3)x x f x e x m e x =-+≥-+，……7分令()3ln(3)x h x e x =-+，1()33xh x e x '=-+，易知1()33xh x e x '=-+在(3,)-+∞单调递增，221(2)331023h e e --'-=-=-<-+，1111(1)330132h e e --'-=-=->-+，设0001()303xh x e x '=-=+，则0(2,1)x ∈--，当0(3,)x x ∈-时，()0h x '<，当0(,)x x ∈+∞时，()0h x '>；所以()h x 在0(3,)x x ∈-上单调递减，0(,)x x ∈+∞上单调递增，……9分所以0m i n 00()()3l n (3)x h x h x e x ==-+，又因为0001()303x h x e x '=-=+，故00133x e x =+， 所以01ln3l nl n 3x e x +=+，即00ln3ln(3)x x +=-+，所以0min 00()()3ln(3)x h x h x e x ==-+001ln 33x x =+++001(3)3ln 33x x =++-++3ln 3≥+ln 31=- 当且仅当00133x x =++，即02x =-或04x =-时等号成立，而0(2,1)x ∈--，所以mi n ()ln 31h x >- 即()ln31h x >-，所以()ln 31f x >-.……12分20.解：（Ⅰ）连接BC ，因为AB 是圆O 的直径，所以90ACB ∠=，所以90B BAC ∠+∠= ，因为AD CE ⊥，所以90ACD DAC ∠=∠= ,因为AC 是弦，且直线CE 和圆O 切于点C ， 所以 ACD B ∠=∠，所以DAC BAC ∠=∠, ………5分 （Ⅱ）由（Ⅰ）知ABC ∆∽ACD ∆,所以AC ADAB AC=， 由此得2AC AB AD =⋅， 因为2OB =，1AD =，所以4AB =，且2414AC A B AD =⋅=⨯=，所以2AC =，又1AD =，故2AC AD =，又AD CE ⊥，于是30ACD ∠=，因为ACD B ∠=∠，所以30B ∠=，30BFD ∠=，故BC CF =，因为CF 与圆O 相切，由切割线定理得2CF AF BF =⋅，所以2BC AF BF =⋅，即BC AFBF BC=． 21.解：（Ⅰ）由直线l 的参数方程得：34yx m =+⋅, 所以，直线l 的普通方程为4340x y m --=；由cos 24cos ρρθθ=+得：()2222cos sin 4cos ρρθθρθ=-+，即22y x =，所以，曲线C 的普通方程为22y x =．（Ⅱ）因为()0,m P ，直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧=+=t y t m x 5453（t 为参数），将其代入22y x =得：21632255t m t ⎛⎫=+ ⎪⎝⎭，即2815250t t m --=， 由2258000m ∆=+>得932m >-，12158t t +=，12258mt t =-， 因为AB 是PA 与PB 的等比中项，所以2AB PA PB =⋅，即21212()t t t t -=， 所以2121212()4t t t t t t +-=显然当0m ≥时不满足题意，于是0m <， 所以21212()5t t t t +=，即215255()88m ⎛⎫=- ⎪⎝⎭，所以940m =-．22.解：(Ⅰ) 当1a =-时，不等式()130f x x ++-≤即为不等式21130x x -++-≤不等式21130x x -++-≤同解于：1330x x <-⎧⎨--≤⎩ 或 11210x x ⎧-≤≤⎪⎨⎪--≤⎩ 或 12330x x ⎧>⎪⎨⎪-≤⎩， 解得：∅ 或 112x -≤≤或 112x <≤，所以不等式()130f x x ++-≤的解集为[]1,1-.(Ⅱ) 因为[]1,2x ∀∈，2()1f x x <+恒成立，即[]1,2x ∀∈，221x a x +<+恒成立， 而221x a x +<+⇒22121x x a x --<+<+ ⇒222121x x a x x ---<<-+，即[]1,2x ∀∈，222121x x a x x ---<<-+恒成立，设()221g x x x =---，()221h x x x =-+可转化为[]1,2x ∀∈，()()max min g x a h x <<，即40a -<< 所以a 的取值范围是()4,0-.。

云南省昆明市第一中学2017届高三数学上学期第二次双基检测试题文（扫描版）昆明市第一中学2017届摸底考试 参考答案（理科数学）一、选择题1. 解析：集合{2,1}M =-，{}|0N x x =<，所以{}2M N -=I ，选C ．2. 解析：因为2i12i iz -==--，所以12i z =-+，选B ． 3. 解析：由已知l β⊄，所以B ，D 正确；由面面平行的性质知C 正确；对于A ，//,l ααβ⊥，则l 与β相交或平行都有可能，选A ． 4. 解析：()()()44411111x x x a x x a +++=+⎪⎭⎫ ⎝⎛+∴()411x x a +⎪⎭⎫ ⎝⎛+展开式中2x 的系数为0463424=+=+⋅a C C a ∴32-=a ，选B ．5. 解析：因为2222123410s =-+-+=，选A ．6. 解析：因为等差数列{}n a 中，3a ，5a ，10a 成等比数列，所以()()()2111429a d a d a d +=++，所以123a d=-，而()()41411102233d S a a a a d =+=++=，故21203a d d =-<，且241003dS d =>，选C ．7. 解析：取AC 中点D ，连接,BD PD ，由正视图和侧视图得BD ⊥平面PAC ，PC ⊥平面ABC ，则90BDP ︒∠=，且BD PD =PB =C ．8. 解析：因为40.41033a ===，30.310441b ===>，所以1a b >>，而4log 31<，所以a b c >>，选A ．9. 解析：作出可行域得到点316,55A ⎛⎫⎪⎝⎭，26,55B ⎛⎫- ⎪⎝⎭，184,55C ⎛⎫- ⎪⎝⎭，由于)0(<+=k y kx z 的最大值为5，则目标函数的图像必经过点)5,0(，当0<k 时，由图可知只有经过点B 的直线符合条件，选D ．10. 解析：xax x a x x x f 11)(2+-=-+=' ，)0(>x当22<<-a 时，12+-ax x 恒大于零，所以0)(>'x f ，故)(x f 单调递增，无极值，A 正确；当2>a 时，令0)(='x f ，解得2421--=a a x ，2422-+=a a x ，可知)(x f 在()1,0x 和()+∞,2x 单调递增，在()21,x x 单调递减，)(x f 在2x x =处取得极小值，而2110x x <<<，所以023)1()(2<-=<a f x f ，B 正确； 当2=a 时，0)1(1221)(22≥-=+-=-+='xx x x x x x x f ，)(x f 单调递增，无极值，C 错误；又当0→x 时，0)(<x f ，当+∞→x 时，0)(>x f ，而且)(x f 的图像连续，所以)(x f 必有零点，D 正确，选C ．11. 解析：由双曲线的对称性可知2ABF ∆是等腰三角形，且2AF B ∠是钝角，所以2121422AF F AF B ππ<∠=∠<，所以21tan 1AF F ∠>, 即1121AF F F >，又21b AF a =，所以212b ac>，即222c a ac ->，化简得2210e e -->，解出1e >，选B. 12. 解析：设直线:AB x y n -=，即x y n =+代入22y x =得2220y y n --=，则122y y +=，12122y y n =-=-，所以14n =.设AB 的中点为00(,)M x y ，则121212x x y y +=++52=，所以120524x x x +== ，12012y y y +==，又点M 在直线x y m +=上，所以0094m x y =+=， 选D ． 二、填空题13. 解析：以点B 为坐标原点，以BC 的方向为x 轴的正方向，以BA 的方向为y 轴的正方向建立平面直角坐标系，得()6,8AC =-，()3,4BD =，所以183214AC BD ⋅=-=-．14. 解析：要求事件的概率为2426128033243C ⎛⎫⎛⎫⋅⋅=⎪ ⎪⎝⎭⎝⎭． 15. 解析：依题意，得()sin(22)g x x ϕ=+，因为2|)()(|21=-x g x f ，所以不妨设ππk x 2221+=，22222x m πϕπ+=-+，所以12()2x x k m πϕπ-=++-，又因为12min6x x π-=，且02πϕ<<，所以26ππϕπ+-=-，所以3πϕ=．16. 解析：由已知得212a a -=，2322a a -=-， 3432a a -=，4542a a -=-， …8982a a -=-，91092a a -=；累加得2341012222a a -=-+-+ …()()9892122234212⎡⎤--⎣⎦-+==--，所以10341a =.三、解答题17. （Ⅰ）证明：由tan b a B =及正弦定理得sin sin cos sin B b BB a A==， 因为ABC ∆中，sin 0B ≠， 所以cos sin B A =，即sin sin 2B A π⎛⎫+=⎪⎝⎭； 由A 为钝角，所以, 22B πππ⎛⎫+∈ ⎪⎝⎭， 故2B A π+=，即2A B π-=. ………5分（Ⅱ）解：因为2A B π=+，所以(2)2022C B B πππ=-+=->，故04B π<<；所以()2sin 2sin sin 2cos 2sin 212sin B C B B B B +=+=+-21334sin 816B ⎛⎫=--+ ⎪⎝⎭，由0sin B <<2133334sin 81616B ⎛⎫<--+≤ ⎪⎝⎭，所以sin 2sin B C +的取值范围.是33 16⎤⎥⎝⎦. ………12分18. 解：（Ⅰ）证明：连接AC ，因为四边形ABCD 是菱形，F 为BD 中点，所以F 为AC中点．又因为E 为PA 中点，所以//EF PC ，又EF ⊄平面PBC ，PC ⊂平面PBC ， 所以//EF 平面PBC ． ………5分 （Ⅱ）取AD 中点O ，连接,OB OP ，因为PA PD =，所以PO AD ⊥；因为菱形ABCD 中，AB AD =，60BAD ︒∠=，所以ABD ∆是等边三角形，所以BO AD ⊥，由已知BO PO =，若PB =，由222BO PO PB +=得PO BO ⊥．如图，分别以,,OA OB OP 所在直线为x 轴，y 轴，z轴建立空间直角坐标系Oxyz -，由题意得13(1,0,,(0,3,0)(1,0,0),(,0,3),(,0,0)2222A B D P E F --，3(2DE =1(2DF =，设平面DEF 的一个法向量为(,,)n x y z =，由0,0,n DE n DF ⎧⋅=⎪⎨⋅=⎪⎩得30,210,2x z x y ⎧=⎪⎪⎨⎪=⎪⎩ 由此可取(3,1,3)n =-， 又因为平面ABD 的法向量OP =， 又313cos ,n OP n OP n OP⋅<>==⋅，故2sin ,n OP <>=， 即二面角E DF A --． ………12分 19. 解：（Ⅰ）设事件A 为“甲同学选中丽江景点”、 事件B 为“乙同学选中丽江景点”， 则()122323C P A C ==, ()243535C P B C ==． (3)分因为事件A 与事件B 相互独立，故甲同学选中丽江景点且乙同学未选中丽江景点的概率为()()()2243515P AB P A P B ==⨯=． (5)分（Ⅱ）设事件C 为“丙同学选中丽江景点”则()243535C P C C ==．X 的所有可能取值为0,1 ,2,3 ． (7)分()()1224035575P X P ABC ===⨯⨯=．()()()()22213212320135535535575P X P ABC P ABC P ABC ==++=⨯⨯+⨯⨯+⨯⨯=．()()()()23222313333235535535575P X P ABC P ABC P ABC ==++=⨯⨯+⨯⨯+⨯⨯=．()()23318335575P X P ABC ===⨯⨯=． (9)分X 的分布列为：75X 的数学期望为：()42033182801237575757515E X =⨯+⨯+⨯+⨯=． ………12分20. 解：（Ⅰ）由已知得221314a b += ① 又 2214c b a a =⇒= ②联立①、②解出24a =，21b =所以椭圆的方程是 2214x y += 4⋅⋅⋅⋅⋅⋅⋅⋅⋅分 （Ⅱ）当l的斜率不存在时，11(),()22C D -，此时120S S -=；当l 的斜率存在时，设:l (0)y k x k =≠，设1122(,),(,)C x y D x y ，联立直线方程与椭圆方程消y 得2222(41)(124)0k x x k +++-=，所以212214x x k+=-+，212212414k x x k -=+. 所以12121222S S y yy y -=-=+122()k x x =++=，由于0k ≠，所以12S S-4k k=≤=+4k =1k时，即12k =±时，12S S -=12S S-⎡∈⎣12⋅⋅⋅⋅⋅⋅⋅⋅⋅分. 21. 解: (Ⅰ) 函数()f x 的定义域为()0,+∞ ………1分因为221ln 2(1)()(1)x xf x f x x x+-''=++， ………2分 所以1(1)2(1)2f f ''=+，即1(1)2f '=-， 所以ln 1()1x f x x x=++，221ln 1()(1)x xx f x x x +-'=-+， ………4分 令1x =，得(1)1f =， 所以函数()f x 在点(1,(1))f 处的切线方程为11(1)2y x -=--,即230x y +-=. ………5分(Ⅱ) 因为22ln 11()(2ln )11x x f x x x x x--=+--, ………6分令21()2ln x g x x x -=+，则222221(1)()x x x g x x x -+--'==-，因为1x ≠，所以()0g x '<，所以()g x 在()0,1，()1,+∞上为减函数,………8分 又因为(1)0g =，所以，当1x >时，()(1)0g x g <=，此时，21()01g x x ⋅>-； 当01x <<时，()(1)0g x g >=，此时，21()01g x x⋅>-， ………10分假设2ln 2ln 1()()11x x h x f x x x x=-=+--有最小值b (0)b >，则()0h x b -≥， 即22ln 101x b x x +-≥-. 若1b >，当1(,1)x b∈时，()0h x b -<； 若01b <≤，当1(,)x b∈+∞时，()0h x b -<，所以，不存在正数b ，使()h x b ≥. 所以，当0x >，且1x ≠时，ln ()01x f x x ->-，所以，220a a --≤， 解得：12a -≤≤ . ………12分 第22、23题中任选一题做答，如果多做，则按所做的第一题记分。

机密★启用前【考试时间：12月1日9: 00-11: 30】昆明第一中学2016届高中新课标高三第三次双基检测文科综合试卷本试卷分第1卷（选择题）和第Ⅱ卷（非选择题）两部分。

满分300分，考试时间150分钟。

第I卷（选择题，共140分）本卷共35个小题，每小题4分，共140分，在每小题给出的四个选项中，只有一项是符合题目要求的。

图l为2012年我国新疆LNC（液化天然气）站点分布图。

读图完成l~2题。

1．影响新疆LNC站点分布的主要因素是A．资源B．市场C．交通 D. 技术2．我国将在今后若干年内大力建设LNC站点，其建设的主要意义是A．大大改善我国大气质量B．促进西气东输工程建设C．积极推动我国新能源汽车发展D．减轻我国东部地区能源短缺压力图2为顿河流域略图及齐姆良斯克水库区气候资料图。

读图完成3—4题。

3．甲海区比乙海区A．含沙量较小B．盐度较低C．结冰期较短。

D．污染更小4．与顿河汛期、齐姆良斯克灌溉区的自然植被和土壤对应的是A．春汛、草原、黑钙土B, .春汛、荒漠、荒漠土C．夏汛、针叶林、灰化土D．冬汛、常绿硬叶林、红壤某地理兴趣小组对长江流域主要省市土地利用进行调研，得出‚2011年长江流域各省市部分土地利用结构图‛（图3，广东、福建面积极少未计入）。

读图完成5~6题。

5．核对数据肘，有同学发现中西部地区某省份数据存在一处明显错误，该省份是A．甘肃B．云南．C．四川D．陕西6．图4为长江流域某土地利用类型比重示意图，该土地利用类型为A．水域B．耕地C．林地n草地、长江作用和鄱阳湖作用影响江一湖的水量交换强度，图5为近年来长江与鄱阳湖作用的频率分布图。

读图完成7-8题。

7．对江湖相互作用的季节变化特征和原因叙述正确的是A．长江作用主要发生在夏秋季，鄱阳湖作用主要在冬春季B．5 -6月降水集中在长江以南，鄱阳湖流域入湖流量迅速增加C．7 -8月锋面雨带在长江下游，长江汇流量增加，使长江作用增强D．9月锋面雨带返回长江以南，鄱阳湖作用强度明显加大8．引起江湖相互作用此消彼长的主要原因有①地势平坦②降水时空差异③水到设施控制④水资源消耗差异A．①②B．②③C．③④D．②④新加坡是亚洲与大洋洲的航空枢纽，也是伦敦到悉尼的重要航空中转站。

昆明一中第三期月考语文答案第Ⅰ卷阅读题甲必考题一、现代文阅读（9分，每小题3分）1.C（本题考查理解文中重要语句的能力。

原文中说的是“图像作为表述人类对自身和世界的欲望映像，强化了人类根深蒂固的自恋情结——人类的自身经验被最大程度地转化为满足人类意愿的观看的对象”。

选项中偷换了原文中的概念，把“人类的自身经验”换成了图像。

）2.D（本题考查概括归纳内容要点的能力及对重要语句的理解。

原文中“数字时代，网络似乎在构筑人类与机器的边界，但又不断让技术更吸引人，让人与机器更加唇齿相依。

”原文的意思是技术变得更加吸引人，会让人与机器的关系更加密切，但并非就可以消除对机器的恐惧和敌意。

选项中“只要……就……”的表述过于绝对。

）3.D（本题考查概括归纳内容要点和作者观点的能力。

作者的意思是，在数字时代，艺术的存在方式发生了重大的变化，与传统艺术相比给人带来的效用也不相同。

艺术只是发生了变化，我们需要重新认知艺术而并非艺术难以继续生存。

）二、古代诗文阅读（36分）（一）文言文阅读（19分）4.B5.C（尚书是各部长官，副长官叫“侍郎”。

）6.C（太子是杀死皇帝反叛。

“弑”是“臣杀君，子杀父”之意。

）7.（1）现在城内粮食匮乏，百姓无心固守，只是因为城门紧锁，戒备森严，逃不了罢了。

（大意3分，“但”、“扃”各1分）（2）张畅派门生荀僧宝进京，通过颜竣陈述刘义宣准备反叛的征兆情况。

（大意3分，“陈”与“衅”各1分）【参考译文】张畅字少微，是吴郡人。

张畅少年时候与堂兄张敷、张演、张敬齐名，是后辈中的杰出人才。

最初开始做官时担任太守徐佩之的主簿，徐佩之被处死，张畅便骑马前去奔丧，穿上．．丧服．．极尽哀伤，被当时谈论的人称赞。

他的弟弟张枚曾经被疯狗咬伤，医生说吃蛤蟆可以治好，张枚认为这件事很难做到。

张畅笑着先尝了些，张枚因此才吃，伤口也就痊愈了。

孝武帝镇守彭城，张畅任安北长史、沛郡太守。

元嘉二十七年，魏太武帝拓跋焘南征，太尉江夏王刘义恭统率各路军队前往镇守彭城。

（新课标）云南省昆明市第一中学2017届高三英语第三次双击检测试题（扫描版）第1巻（选择题）第一部分；听力（共两节.满分孔分）第一节（共5小题；毎小題门分，满分7.5分）*「听下面生段对话。

每段对话后有一个小聽，从题中所给的h队C三个选填中选出域住选项.井标在试曲的相应程賣©昕完毎段对话后，你都打血秒沖的时阖来回答有关尔题和阅读下一小题，每段对话仅读-遍「L Whom is tlie man fhrobably speaking to 7C. His mother.A.His iewh«* 吐His colleague.2.What caused Jane¥ depression?扎Ph^icd ilb如. B. Lift erperien* G 科mncial problem.3.Haw many tickets *iD the woman get?扎Ei曲. B+ Ten. 匚 Twelve4.Whit may lhe ^peakffb do ntal?A.Play poker. B- Go outing. G Watch TV*5.What does （he man fed satisfied with?九The weaiheTx 8, Hie haisi-匚弘® 由0&第二节（共计小题；每小ffii-5分.酒分225分）听下面3段对话°毎段对话后有一个小題*从題中所给的趴氛E三个逸项中aajftg选頊’并标在试卷的相应位置"听完每段对话戒建白机，你将有时间闵读各个小题’每小雜5秒钝；听完后, 各个小題将给出5秒钟的作答时闾®每段对话或独白读两遍“听下面一段材料，回答第6至7题o&p What dees the nun think of the housekeeper?A* She does the basics wel]TB.She1 is »ot rtry nsponsible*C.She just cbe& acme deaning*英ig •第2页〈共8页）7. What do the speakers decide to do finally? A. Give the housekeeper a raise. B ・ Hie a better housekeeper instead ・ C ・ Consider the housekeepers request- 听下面一段材料，回答第8至10题。

理科数学第Ⅰ卷一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项 是符合题目要求的.1.已知集合2{|20,}M x x x x R =+-=∈，{|0,}N x x x R =<∈，则M N =（ ）A ．φB ．{1}C ．{2}-D ．{2,1}-2.已知复数z 满足方程2z i i ∙=-，则z 在复平面上对应点位于（ ） A ． 第一象限 B ．第二象限 C ．第三象限 D ．第四象限3.设,αβ是两个不同的平面，直线l 满足l β⊄，以下命题中错误的命题是（ ） A ．若//,l ααβ⊥，则l β⊥ B ．若//,//l ααβ，则//l β C ．若,//l ααβ⊥，则l β⊥ D ．若,l ααβ⊥⊥，则//l β4. 41()(1)a x x++展开式中2x 的系数为0，则a =（ ） A ．23 B ．23- C. 32 D ．32- 5.执行如图所示的程序框图，若输入数据5N =，则输出的s 结果为（ ） A ． 10 B ．20 C. -15 D ．-66.已知等差数列{}n a 的公差d 不为零，前n 项和是n S ，若3510,,a a a 成等比数列，则（ ） A ．140,0a d dS >> B ．140,0a d dS >< C. 140,0a d dS <> D ．140,0a d dS <<7.三棱锥P ABC -及其三视图中的正视图和侧视图如图所示，则棱PB 的长为（ ） A ．D．8.设0.43a =，0.34b =，4log 3c =，则（ ）A ．a b c >>B ．b c a >> C. c a b >> D ．c b a >>9.已知实数,x y 满足43120220220x y x y x y +-≤⎧⎪-+≥⎨⎪+-≥⎩，若(0)z kx y k =+<的最大值为5，则实数k 的值为（ ）A ．43-B ． -3 C. 2918- D ．192- 10.已知函数21()ln 12f x x x ax =+-+，下列结论中错误的是（ ）A ． 当22a -<<时，函数()f x 无极值B ．当2a >时，()f x 的极小值小于0 C.当2a =时，1x =是()f x 的一个极值点 D ．,()a R f x ∀∈必有零点11.设12,F F 分别是双曲线M ：22221(0,0)x y a b a b-=>>的左、右焦点，过点1F 且垂直于x 轴的直线与双曲线M 交于,A B 两点，若点2F 满足120F A F B ∙<，则双曲线的离心率e 的取值范围是（ ）A．11e <<+ B．1e >+C. 1e <<．e >12.已知抛物线22y x =上有两点1122(,),(,)A x y B x y 关于直线x y m +=对称，且1212y y =-，则m 的值等于（ ）A ．34 B ．54 C. 74 D ．94第Ⅱ卷二、填空题（每题5分，满分20分，将答案填在答题纸上）13.在直角三角形ABC 中，90B ∠=，若8,6AB BC ==，D 为斜边AC 的中点，则AC BD ∙= ．14.某项测试有6道试题，小明同学答对每道题的概率都是13，则小明参加测试（做完全部题目）刚好答对2道试题的概率为 ．15.将函数()sin 2f x x =的图象向左平移(0)2πϕϕ<<个单位后得到函数()g x 的图象，若对满足12|()()|2f xg x -=的12,x x 有12||x x -的最小值为6π，则ϕ= ． 16.已知数列{}n a 满足11a =-，212212n n n a a ---=，22122n n n a a +-=，则10a = ．三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17.（12分）设ABC ∆的内角,,A B C 的对边分别为,,a b c ，A 为钝角，且tan b a B =. （1）证明：2A B π-=；（2）求sin 2sin B C +的取值范围. 18.（12分）如图，在四棱锥P ABCD -中，底面ABCD 是菱形，60BAD ∠=，,E F 分别为,PA BD 的中点，2PA PD AD ===. （1）证明：//EF 平面PBC ；（2）若PB =，求二面角E DF A --的正弦值.19.（12分）甲、乙、丙三名学生计划利用今年“十一”长假从五个旅游景点（五个景点分别是：大理、丽江、西双版纳、峨眉山、九寨沟）中每人彼此独立地选三个景点游玩，其中甲同学必选峨眉山，不选九寨沟，另从其余景点中随机任选两个；乙、丙两名同学从五个景点中随机任选三个.（1）求甲同学选中丽江景点且乙同学未选中丽江景点的概率；（2）用X 表示甲、乙、丙选中丽江景点的人数之和，求X 的分布列和数学期望.20.（12分）已知椭圆Γ：22221(0)x y a b a b +=>>过点(1,P ，左焦点是F ，左、右顶点分别是,A B ，过点F 的直线l 与椭圆Γ相交于,C D 两点. （1）求椭圆Γ的方程；（2）记,ABC ABD ∆∆的面积分别为12,S S ，求12S S -的取值范围.21.（12分）已知函数'ln 2(1)()1x f f x x x=-+. （1）求函数()f x 在点(1,(1))f 处的切线方程； （2）当0x >且1x ≠时，2ln ()(2)1xf x a a x >+---，求a 的取值范围.请考生在22、23三题中任选一题作答，如果多做，则按所做的第一题记分.22.（本小题满分10分）选修4-1：几何证明选讲已知曲线C 的极坐标方程是2cos 4sin ρθθ=+，P 点极坐标为(3,)2π，以极点为平面直角坐标系的原点，极轴为x 轴的正半轴，建立平面直角坐标系xOy ，在平面直角坐标系中，直线l 经过点P ，倾斜角为3π.（1）写出曲线C 的直角坐标方程和直线l 的参数方程； （2）设直线l 与曲线C 相交于,A B 两点，求11||||PA PB +的值.23. （本小题满分10分）选修4-4：坐标系与参数方程 设函数()||f x x m =+.（1）若不等式(1)(2)5f f -+≥，求实数m 的取值范围； （2）当0x ≠时，若1()()f f x a x+-≥恒成立，求a 的最大值.春到四月，如火如荼，若诗似画，美到了极致，美到了令人心醉。

云南省昆明市第一中学2017届高三新课标第三次双击检测理科综合试卷生物试题第I卷一、选择题：1.下列关于细胞结构和功能的叙述，正确的是（）A.硝化细菌的遗传控制中心是拟核B.酵母菌不具有染色体、属于兼性厌氧菌C.植物细胞的系统边界是细胞壁D.动物细胞的细胞质基质能为细胞核提供ATP、酶、DNA等物质2.下列有关囊泡运输的叙述，错误的是( )A.浆细胞产生的抗体经囊泡运输分泌到细胞外B.囊泡运输依赖膜的流动性且不消耗能量C.生物膜之间可通过囊泡的转移实现膜成分的更新D.吞噬细胞摄取、处理抗原与囊泡运输有关系3.韭黄是韭菜经软化栽培变黄的产品，即把韭菜的宿根（茎叶枯萎后根可以继续生存，次年根可重新发芽）放置黑暗条件下培育获得。

下列有关韭黄的叙述，错误的是( )A.夜晚适当降低培育温度可减少韭黄有机物的消耗B.叶片中的叶绿素含量逐渐降低导致其颜色偏黄C.比较韭菜和韭黄叶片泰色素的吸收光谱，在红先和蓝紫光区域都会出现差异D.培育韭黄的过程中叶绿体中ATP的合成速率一直为零4.某基因型为Aa的细胞经分裂形成了aa型的配子，下图为该细胞分裂的不同时期每条染色体上DNA 数目变化(不考虑基因突变和交叉互换)，有关叙述正确的是：A.BC段细胞的基因型为AAaaB.同源染色体的分离发生在C时C.形成aa型配子是因为在CE段染色体未正常进入子细胞D.该图不可表示有丝分裂过程中每条染色体上DNA含量变化5.下列体液调节和神经调节的叙述，错误的是( )A.垂体释放的抗利尿激素能提髙肾脏集合管对水的通透性B.单细胞动物只有体液调节，没有神经谪节和免疫调节C.神经递质与突触后膜上载体的结合具有特异性D.某些腺体的细胞可接受神经递质传递的信息6.某岛屿内一年生的某植物种群，其个体基因型均为aa型，某年外来了许多基因型为AA 的种子，几年后该种群A和a的基因频率分别变化为95%、5%。

以下分析错误的是（）A．该植物种群发生了进化B．该种群所处环境可能没有发生变化C．该植物种群内的个体不是进化的基本单位D．该种群中有95％的个体表现出了更加适应环境的性状第II卷29.（8分）为鉴定一批库存的花生种子的存活率，科研人员用温水浸泡种子，测定了种子呼吸过程中CO2和O2吸收速率，结果如下图：请回答下列问题：（1）种子含水量与细胞呼吸强度密切相关：一方面水是有氧呼吸第阶段的原料；另一方面细胞内自由水/结合水的值（填“增大”、“基本不变”、“减少”）也会影响细胞呼吸强度。

昆明第一中学2017届高中新课标高三第三次双基检测文科综合试卷第I卷（选择题，共140分）本卷共35个小题，每小题4分，共140分，在每小题给出的四个选项中，只有一项是符合题目要求的。

海绵城市是指城市在适应环境变化和应对自然灾害等方面具有良好的“弹性”，下雨时吸水、蓄水、渗水、净水，需要时将蓄存的水“释放”并加以利用。

海绵城市可以把有限的雨水留下来，利用自然力量排水，形成自然积存、渗透、净化的新型城市排水系统。

结合图1完成1~3题。

1．关于海绵城市的叙述，正确的是①城市统一收集雨水②水资源得到充分利用③通过基础设施建设来实现④具有防治内涝和水污染作用⑤实现社会经济和生态综合效益⑥可替代传统的排水系统A.①②⑤B.②③⑤C.③⑤⑥D.①③⑥2．下列可以发挥“海绵城市”作用的是A．游泳池、洒水车B．城市屋顶花园C．城市釉面砖道路D．室外塑胶跑道3．海绵城市运用低影响开发方式，就近收集、存蓄、渗透、净化雨水，主要目的是A．实现雨水在城市中的自然转换和迁移B．改变传统城市建管道排泄雨水的处理方式C．起到节能减排、缓解城市热岛效应的功效D．形成城市绿色景观带和河流、湖泊景观带读澳大利亚区域略图（图2），完成4~5题。

4．图中四地年均降水量大小排序正确的是A．①>②>③>④B．④>②>①>③C．②>①>④>③D．①>④>②>③5．关于图中四地的叙述，错误的是A．①地铁矿最丰富B．②地农业产值最高C．③地太阳能资源最丰富D．④地绵羊养殖最多读北半球某山地1月和7月平均气温垂直分布图（图3），完成6—7题。

6．根据图中信息判断，该山地最有可能位于A．25°N附近B．30°N附近C．35°N附近D．40°N附近-7．关于该山地气温垂直分布的正确说法是A．1月局部范围内大气对流不畅B．1月气温垂直递减率比7月大C．随海拔升高气温年变化增大D．山地顶峰及附近有冰川活动下图为我国某大城市主干街道上的甲、乙两个公交站台分布图，经统计不同时刻上下车人数随时间变化有明显差畀（图4），读图完成8~9题。

云南省昆明市第一中学2016届高三数学上学期第三次双基检测试题文（扫描版）昆明市第一中学2016届高三考试 参考答案（文科数学）命题、审题组教师 丁茵、顾先成、杨仕华、鲁开红、张兴虎、张波、李建民、张宇甜、彭力 一、选择题：本大题共12小题，每小题5分，共60分。

1. 解析：集合|0M x x =>，|0N y y =≥，所以|0M N x x =>I ，选A ． 2. 解析：()()1007100822201520161i i i i i i =-+=+，选A ．3. 解析：画出可行域（如图阴影部分所示）和直线0l ：20x y +=，观察图形，知直线2x y z +=过直线3y x =-+和20x y -=的交点()1,2A 时，z 取得最小值2124⨯+=，选C.4. 解析：设直线l 的方程为+=111x y-，把点C 的坐标代人直线l 的方程得+4=1x -，=3x ，选B. 也可用斜率或者向量的知识解决.5. 解析：第一次循环，11S =，9n =；第二次循环20S =，8n =；第三次循环，28S =，7n =；第四次循环，35S =，6n =，结束循环，输出35S =，因此6n >，选C .6. 解析：4tan()=2πα-，所以tan 121tan αα-=+，即tan 3α=-; 所以2222sin22sin cos 2tan 61cos sin 2cos 2tan 11αααααααα===-+++，选D ． 7. 解析：由 c log =，所以a c >；而61log 2b =,61log 3a =,且66log 3log 20>>，所以b a >；故b a c >>，选C.8. 解析：由题意可知函数12()cos()1(0)f x x ωϕω=++>的图象的一个对称中心为点,112π⎛⎫⎪⎝⎭，一条对称轴为直线4x π=，所以4412T ππ≤-，即232ππω≤，得3ω≥，所以ω的最小值为3，选A. 9. 解析：由于正视图、侧视图、俯视图都是边长为2的正方体，所以此四面体一定可以放在正方体中，所以可以在正方体中寻找四面体，如图所示，四面体ABCD 满足题意，所以四面体的表面积是(24= B.10. 解析：设双曲线C 的左焦点为1F ，在ABF ∆中根据余弦定理有22238=10+2105BF BF -⨯⨯⨯，解得=6BF ，所以=90AFB ︒∠，连结1AF ，1BF ，可知四边形1AFBF 为平行四边形，122===10c F F AB ，12==2a AF AF -，2==52ce a，选C ． 11. 解析:依题意得函数()f x 的图像恒过定点(1, )e ，A 错；当1m =-时，函数ln y x=与函数x y e =的图像无公共点，所以此时函数()f x 不存在零点，B 错；因为函数()f x 的定义域为0 +∞（，），所以对于任意的0 +m ∈∞（，），()0xm f x e x'=+>， 故函数()f x 是增函数，C 错；由()xx m m xe f x e x x+'=+=， 令()x g x xe m =+，由()(1)0x g x e x '=+>得函数()g x 是增函数，所以()(0)g x g m >=，因为(,0)m ∈-∞，故存在0x ，使0()0f x '=，且当0(0,)x x ∈时，()0f x '<，当0(,)x x ∈+∞时，()0f x '>，所以函数()f x 存在极小值，选D.12. 解析: 2()32f x x ax b '=++，由已知得()0f x '=的两根分别在, 1（0）及1, 2（）内，且(0)0(1)0(2)0f f f '>⎧⎪'<⎨⎪'>⎩， 即02304120b a b a b >⎧⎪++<⎨⎪++>⎩而22(1)(4)a b ++-表示点(,)P a b 与点, 4Q(-1）的距离的平 方，如图，所求的范围是(5, 20)，选B .二、填空题：本大题共4小题，每小题5分，共20分。