抛物型方程数值解

抛物型方程的Galerkin有限元方法一、引言抛物型方程是一类常见的偏微分方程，具有广泛的应用。

在数值解中，Galerkin有限元方法是一种常用且有效的方法。

本文将介绍抛物型方程的基本概念，并详细讲解Galerkin有限元方法在求解抛物型方程中的应用。

二、抛物型方程的基本概念抛物型方程是指具有二阶时间导数和二阶空间导数的偏微分方程。

一般形式为：∂u−Δu=f∂t其中，u为未知函数，t为时间变量，Δ为Laplace算子，f为给定的函数。

抛物型方程的一个重要特点是初始条件和边界条件对解的影响非常大。

合适的初始条件和边界条件能够唯一确定方程的解。

三、Galerkin有限元方法Galerkin有限元方法是一种利用函数空间进行近似的数值计算方法。

它基于以下思想：将问题的解表示为函数空间中的一个函数，通过求解一组代数方程组来近似求解原始方程。

1. 函数空间的选择在应用Galerkin有限元方法求解抛物型方程时，需要选择合适的函数空间。

常用的函数空间有有限维函数空间和无限维函数空间。

具体的选择需要根据问题的特点和计算的要求来确定。

2. 弱形式的推导对于抛物型方程，我们可以将其转化为弱形式。

弱形式是通过将方程两边乘以一个测试函数，并进行积分得到的。

这样可以减小对解的要求，并使得问题更容易求解。

3. 数值离散和代数方程的建立接下来，需要对时间和空间进行离散。

通常使用网格来进行离散，将时间和空间分割为有限个小区域。

然后，通过选择适当的基函数，在每个小区域上近似原方程的解。

最终得到一组代数方程组。

求解代数方程组是Galerkin有限元方法的最后一步。

可以使用常用的数值方法，如迭代法、直接法等，来求解代数方程组。

根据计算要求和问题特点，选择合适的求解方法。

四、应用案例以一维热传导方程为例，展示Galerkin有限元方法在求解抛物型方程中的应用。

热传导方程是一个典型的抛物型方程，描述了物体内部的温度分布随时间变化的规律。

二维抛物型方程的广义galerkin方法二维抛物型方程的广义Galerkin方法引言：二维抛物型方程广义Galerkin方法是一种数值计算方法，用于求解二维抛物型偏微分方程。

在许多科学和工程领域中，二维抛物型方程是非常重要的模型，例如热传导方程、扩散方程等。

本文将介绍广义Galerkin方法的基本思想、数学原理以及求解步骤，并通过一个例子来说明其应用。

一、广义Galerkin方法的基本思想广义Galerkin方法是一种弱形式求解偏微分方程的方法，其基本思想是通过将原方程乘以一个试探函数，然后在整个计算域上进行积分，通过适当的近似和转化，将原方程转化为一组离散的代数方程。

广义Galerkin方法通过这种离散化的方式，将连续的偏微分方程转化为离散的代数方程，从而实现了数值求解。

二、广义Galerkin方法的数学原理1. 试探函数空间和测试函数空间的选择：广义Galerkin方法中，我们需要选择适当的试探函数空间和测试函数空间。

通常情况下，我们选择的试探函数空间和测试函数空间是具有一定光滑性质的函数空间，例如Sobolev空间。

2. 弱形式的推导：将原方程乘以一个试探函数，并在整个计算域上进行积分，得到一个弱形式的方程。

这个弱形式的方程通常是具有更好的可求解性质的。

3. 离散化：通过适当的近似和转化，将弱形式的方程转化为一组离散的代数方程。

通常情况下，我们使用一组基函数来近似试探函数和测试函数，并通过在有限元网格上进行积分，将积分方程离散化为代数方程。

三、广义Galerkin方法的求解步骤1. 确定试探函数和测试函数空间：根据问题的特点和要求，选择合适的试探函数和测试函数空间。

2. 推导弱形式：将原方程乘以试探函数，并在整个计算域上进行积分，得到弱形式的方程。

3. 离散化：选择适当的基函数，通过在有限元网格上进行积分，将弱形式的方程离散化为代数方程。

4. 求解代数方程：通过求解离散化的代数方程，得到数值解。

抛物型方程的差分方法抛物型方程是描述物理现象中的薄膜振动、热传导、扩散等过程的方程，具有非常重要的应用价值。

差分方法是一种常用的数值计算方法，用于求解微分方程，对于抛物型方程的数值求解也是非常有效的方法之一、本文将介绍抛物型方程的差分方法，并具体讨论用差分方法求解抛物型方程的一些具体问题。

首先，我们来介绍一下抛物型方程的一般形式。

抛物型方程一般可以表示为：∂u/∂t=α(∂^2u/∂x^2+∂^2u/∂y^2)其中，u(x,y,t)是待求函数，t是时间，x和y是空间变量，α是常数。

这个方程描述的是物理过程中的扩散现象，如热传导过程、溶质的扩散过程等。

差分方法的基本思想是将求解区域离散化为一个个网格点，然后在每个网格点处用近似的方式来计算待求函数的值。

差分方法的求解步骤主要包括以下几个方面：1.选择适当的网格和步长。

在求解抛物型方程时，需要确定空间变量x和y所在的网格点以及步长，同时也需要确定时间变量t所在的网格点和步长。

通常，我们会选择均匀网格，步长选择合适的值。

2.建立差分格式。

差分格式是差分方法的核心部分，它包括对方程进行近似处理和离散化。

对于抛物型方程，常用的差分格式有显式差分格式和隐式差分格式等。

其中，显式差分格式的计算速度快，但是有一定的稳定性限制，而隐式差分格式的稳定性较好，但是计算量较大。

因此，在具体问题中需要根据实际情况选择适当的差分格式。

3.编写计算程序。

在建立差分格式后，需要编写计算代码来求解离散方程。

具体编写的过程包括定义初始条件、建立迭代计算过程、以及计算结果的输出等。

4.计算结果的验证与分析。

求解方程后，需要对计算结果进行验证和分析，主要包括对数值解和解析解的比较、对误差的估计和控制等。

在具体求解抛物型方程时，还会遇到一些问题，例如边界条件的处理、稳定性和收敛性的分析等。

下面将对其中一些问题进行详细讨论。

1.边界条件的处理。

边界条件对差分格式的求解结果有着重要的影响，常见的边界条件包括固定端（Dirichlet）边界条件和自由端（Neumann）边界条件等。

10_抛物型方程的有限差分方法抛物型方程是一类常见的偏微分方程，广泛应用于自然科学和工程学的领域中。

有限差分方法是一种常用的数值求解抛物型方程的方法之一、本文将介绍抛物型方程的有限差分方法（II）。

有限差分方法主要基于离散化的思想，将偏微分方程转化为差分方程，进而求解差分方程的数值解。

对于抛物型方程，其一般形式可以表示为：∂u/∂t=Δu+f(x,t)其中，u(x, t)是未知函数，表示空间位置x和时间t上的解，Δu表示Laplace算子作用于u的结果，f(x, t)是已知函数。

有限差分方法的基本思想是将空间和时间域进行离散化，将连续的空间和时间划分为有限个网格点，然后使用差分近似代替偏导数，得到差分方程。

假设空间域被划分为Nx个网格点，时间域被划分为Nt个网格点，对于每个网格点(i,j)，可以表示为(x_i,t_j)，其中i=0,1,...,Nx，j=0,1,...,Nt。

在有限差分方法中，我们使用中心差分近似来代替偏导数。

对于时间导数，可以使用向前差分或向后差分，这里我们使用向前差分，即：∂u/∂t≈(u_i,j+1-u_i,j)/Δt对于空间导数，可以使用中心差分，即：∂^2u/∂x^2≈(u_i-1,j-2u_i,j+u_i+1,j)/Δx^2将上述差分近似代入抛物型方程中，可以得到差分方程的离散形式：(u_i,j+1-u_i,j)/Δt=(u_i-1,j-2u_i,j+u_i+1,j)/Δx^2+f_i,j其中，f_i,j=f(x_i,t_j)。

重排上式，可以得到递推关系式：u_i,j+1=αu_i-1,j+(1-2α)u_i,j+αu_i+1,j+Δt*f_i,j其中，α=Δt/Δx^2通过设置初始条件和边界条件，可以利用以上递推关系式得到抛物型方程的数值解。

总结来说，抛物型方程的有限差分方法（II）是一种常用的数值求解抛物型方程的方法。

它基于离散化的思想，将偏微分方程转化为差分方程，然后利用中心差分近似代替偏导数，得到差分方程的离散形式。

二维抛物型方程的交替方向隐格式二维抛物型方程的交替方向隐格式是一种数值解法，用于求解二维抛物型方程的数值解。

这种解法将二维问题分解为两个一维问题，并采用隐式差分方法来求解。

具体来说，二维抛物型方程可以表示为：u_t = a^2 u_{xx} + b^2 u_{yy} + f(x,y,u)其中，u是待求解的函数，t是时间，a和b是两个不同的参数，f是右侧的非线性函数。

为了求解这个问题，我们可以采用交替方向隐式差分方法，将问题分解为两个一维问题：1、在x方向上，从左到右扫描每一行数据，更新每个点的u值。

这个过程可以使用隐式差分方法来实现：u^[i,j]^(n+1) = u^[i,j]^(n) + dt a^2 (u^[i+1,j]^(n) - 2u^[i,j]^(n) + u^[i-1,j]^(n)) / h^2 + dt f^[i,j]^(n) 其中，u^[i,j]^(n)表示第n个时间步中，位置为(x[i],y[j])的点的u值，h是x方向上的步长，dt是时间步长，f^[i,j]^(n)表示第n个时间步中，位置为(x[i],y[j])的点上的非线性函数f的值。

2. 在y方向上，从上到下扫描每一列数据，更新每个点的u值。

这个过程也可以使用隐式差分方法来实现：u^[i,j]^(n+1) = u^[i,j]^(n) + dt b^2 (u^[i,j+1]^(n) - 2u^[i,j]^(n) + u^[i,j-1]^(n)) / h^2 + dt f^[i,j]^(n) 其中，u^[i,j]^(n)表示第n个时间步中，位置为(x[i],y[j])的点的u值，h是y方向上的步长，dt是时间步长，f^[i,j]^(n)表示第n个时间步中，位置为(x[i],y[j])的点上的非线性函数f的值。

通过交替更新每个点的u值，我们可以逐步逼近方程的数值解。

这种解法具有二阶精度和稳定性，可以应用于多种二维抛物型方程的问题。

pde 方程抛物型偏微分方程及其应用引言：偏微分方程（Partial Differential Equation，简称PDE）是数学中的一个重要分支，它描述了自然界中的许多现象和规律。

本文将重点介绍一类常见的PDE方程——抛物型偏微分方程，以及它在物理、工程等领域中的应用。

一、抛物型偏微分方程的定义和特点抛物型偏微分方程是指具有一阶时间导数和二阶或更高阶空间导数的偏微分方程。

其一般形式可以表示为：∂u/∂t = a∂²u/∂x² + bu + c其中，u代表未知函数，t和x分别表示时间和空间变量，a、b和c 为常数。

抛物型偏微分方程具有以下特点：1. 方程中包含时间导数，因此描述的是随时间变化的系统或现象。

2. 方程中包含二阶或更高阶空间导数，因此描述的是具有扩散、传导等特性的系统或现象。

3. 方程中的系数a、b和c可以是常数，也可以是与时间和空间变量有关的函数。

二、抛物型偏微分方程的应用抛物型偏微分方程在物理、工程等领域中具有广泛的应用。

以下是其中几个典型的应用：1. 热传导方程热传导方程是抛物型偏微分方程的一个重要应用。

它描述了物体内部的温度分布随时间的变化规律。

热传导方程在热学、材料科学等领域中有广泛的应用，如研究材料的热稳定性、热传导性能等。

2. 扩散方程扩散方程也是抛物型偏微分方程的一种应用。

它描述了物质在空间中的扩散过程，如溶质在溶液中的扩散、气体的扩散等。

扩散方程在化学反应、生物学、环境工程等领域中有重要的应用价值。

3. 粘弹性流体方程粘弹性流体方程是一类描述粘弹性流体流动行为的抛物型偏微分方程。

它在流体力学、工程领域中有广泛的应用，如石油工程中的油藏模拟、地下水流动模拟等。

4. 扩散反应方程扩散反应方程是描述物质在扩散和反应过程中的变化规律的抛物型偏微分方程。

它在化学动力学、生物学等领域中有重要的应用，如描述化学反应速率、生物体内物质传输等。

三、抛物型偏微分方程的数值解法由于抛物型偏微分方程的解析解往往难以求得，因此需要采用数值方法进行求解。

抛物方程的pod-galerkin外推解法研究抛物方程是一类常见的偏微分方程，描述了许多物理现象，例如热传导、扩散等。

对于抛物方程的数值解法研究，其中一种有效的方法是使用有限元方法进行离散化和求解。

在有限元方法中，通常采用Galerkin方法来离散化抛物方程。

该方法将抛物方程转化为一组线性方程组，通过求解这组方程组得到数值解。

然而，Galerkin方法的求解过程中，需要计算大量的内积和矩阵操作，对于大规模问题，计算量较大，耗时较长。

为了提高抛物方程的求解效率，一种有效的方法是使用POD-Galerkin外推解法。

POD (Proper Orthogonal Decomposition) 是一种基于数据的降维方法，通过提取空间中具有最大能量的主成分来近似原始数据。

在POD-Galerkin外推解法中，先利用POD对抛物方程的解进行逼近，然后使用Galerkin方法进行离散化和求解。

POD-Galerkin外推解法的基本思想是，利用POD构建一个近似解空间，然后将原始问题在该空间中进行求解。

通过选取适当的POD基函数，可以减小原始问题的维度，从而降低计算复杂度。

此外，POD-Galerkin外推解法还可以提高数值解的精度和稳定性。

研究表明，POD-Galerkin外推解法在抛物方程的数值计算中具有很好的效果。

它可以显著减少计算时间和存储空间，并提高数值解的精确度。

然而，POD-Galerkin外推解法的实现较为复杂，需要对抛物方程的特性以及POD技术有一定的了解。

总结起来，抛物方程的POD-Galerkin外推解法是一种有效的数值解法，可以用于提高抛物方程求解的效率和精度。

它在科学计算和工程应用中具有重要的意义。

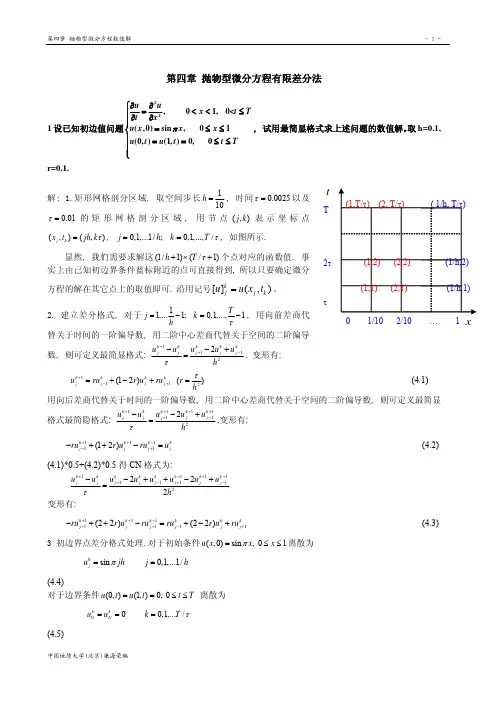
第四章 抛物型微分方程有限差分法1设已知初边值问题22, 01, 0<(,0)sin , 01(0,)(1,)0, 0 u ux t t x u x x x u t u t t T π⎧∂∂=<<⎪∂∂⎪⎪=≤≤⎨⎪==≤≤⎪⎪⎩T ≤, 试用最简显格式求上述问题的数值解。

取h=0.1,r=0.1.0 1/10 2/10 … 1 T 2τ τt解: 1.矩形网格剖分区域. 取空间步长1, 时间2510h =0.00τ=以及0.01τ=的矩形网格剖分区域, 用节点)表示坐标点(,j k (,)(,)j k x t jh k τ=, 0,1,...1/; 0,1,...,/j h k T τ==, 如图所示.显然, 我们需要求解这(1/1)(/1)h T τ+×+个点对应的函数值. 事实上由已知初边界条件蓝标附近的点可直接得到, 所以只要确定微分方程的解在其它点上的取值即可. 沿用记号[]k(,)j j k u x t =。

u 2. 建立差分格式, 对于11,...1; 0,1,...,1Tj k hτ=−=−, 用向前差商代替关于时间的一阶偏导数, 用二阶中心差商代替关于空间的二阶偏导数, 则可定义最简显格式:1122k k k k k1jj j j u u u u u h ++−+=. 变形j τ−−有:1112(12) (k k k kj j j j u ru r u ru r h τ+−+=+−+=(4.1)用向后差商代替关于时间的一阶偏导数, 用二阶中心差商代替关于空间的二阶偏导数, 则可定义最简显格式最简隐格式:111122k k k k k j jj j j u u u u u h τ++++−−+=11+−1kj +,变形有:1111(12) k k k j j j ru r u ru u ++−−−++−= (4.2)(4.1)*0.5+(4.2)*0.5得CN 格式为:111112222k k k k k k k k j jj j j j j j u u u u u u u u h τ+++−+−−++−+=111++−1kj +x x变形有:111111(22)(22) k k k k k j j j j j ru r u ru ru r u ru ++−−+−−++−=+−+ (4.3)3 初边界点差分格式处理.对于初始条件u x (,0)sin , 01=π≤≤h 离散为(4.4)0sin 0,1,...1/j u jh j π==对于边界条件离散为(0,)(1,)0, 0 u t u t t T ==≤≤00 0,1,.../k k N u u k T τ===(4.5)总结: 联立方程(4.1)(4.4)(4.5)得到已知问题的最简显格式差分方程组:11100(12)1 1,...1; 0,1,...,1sin 0,1,...1/0 0,1,.../k k k k j j j j jk k N u ru r u ru T j k h u jh j h u u k T τπτ+−+⎧=+−+⎪⎪=−=−⎪⎨⎪==⎪⎪===⎩ 联立方程(4.2)( 4.4)( 4.5)得到已知问题的最简隐格式差分方程组:1111100(12) 1 1,...1; 0,1,...,1sin 0,1,...1/0 0,1,.../k k k k j j j j jk k N ru r u ru u T j k h u jh j h u u k T τπτ++−−+⎧−++−=⎪⎪=−=−⎪⎨⎪==⎪⎪===⎩ 联立方程(4.3)( 4.4)( 4.5)得到已知问题的CN 格式差分方程组:11111100(22)(22) 1 1,...1; 0,1,...,1sin 0,1,...1/0 0,1,.../k k k k k j j j j j jk k N ru r u ru ru r u ru T j k h u jh j h u u k T τπτ++−−+−⎧−++−=+−+⎪⎪=−=−⎪⎨⎪==⎪⎪===⎩1k j + 4 求解并显示结果利用软件计算(Matlab)如上最简显格式差分方程组.h=1/10;tau=0.0025;T=0.5; r=tau/h^2;M=1/h+1;N=T/tau+1; u=zeros(M,N);for m=1:Mu(m,1)=sin((m-1)*h*pi); endu(1,1:N)=0;u(M,1:N)=0;for n=1:N-1for m=2:M-1u(m,n+1)=r*(u(m+1,n)+u(m-1,n))+(1-2*r)*u(m,n); end end u=u’ 这样我们就计算出不同时刻不同位置k t j x 对应的函数值(,)j k u x t 取tau=0.0025, 即r=0.25绘图, 取tau=0.01, r=1再绘图,如图()图4.2 习题1数值解图示(左r=0.25, 右r=1)2.试构造初边值问题 ()()()()(), 0.51, 0,,0, 0.51,0.5,0, 1,0.51,, 0u u x x x T t x x u x x x u ⎪∂u t t u t t T x ϕ⎧∂∂∂⎛⎞=<<<≤⎜⎟⎪∂∂∂⎝⎠⎪⎪=≤≤⎨⎪==−≤≤⎪∂⎩的显格式，并给出其按最大范数稳定的充分条件。

分类号：O241.82本科生毕业论文（设计）题目：一类抛物型方程的计算方法作者单位数学与信息科学学院作者姓名专业班级2011级数学与应用数学创新2班指导教师论文完成时间二〇一五年四月一类抛物型方程的数值计算方法(数学与信息科学学院数学与应用数学专业2011级创新2班）指导教师摘要: 抛物型方程数值求解常用方法有差分方法、有限元方法等。

差分方法是一种对方程直接进行离散化后得到的差分计算格式，有限元方法是基于抛物型方程的变分形式给出的数值计算格式。

本文首先给出抛物型方程的差分计算方法，并分析了相应差分格式的收敛性、稳定性等基本理论问题.然后，给出抛物型方程的有限元计算方法及理论分析。

关键词：差分方法，有限元方法，收敛性，稳定性Numerical computation methods for a parabolic equationYan qian（Class 2, Grade 2011，College of Mathematics and Information Science）Advisor: Nie huaAbstract：The common methods to solve parabolic equations include differential method，finite element method etc。

The main idea of differential method is to construct differential schemes by discretizing differential equations directly. Finite element scheme is based on the variational method of parabolic equations。

In this article, we give some differential schemes for a parabolic equation and analyze their convergence and stability. Moreover，the finite element method and the corresponding theoretical analysis for parabolic equation are established.Key words：differential method，finite element method, convergence，stability1 绪 论1。