抛物型方程的差分方法

抛物型方程的差分方法抛物型方程是描述物理现象中的薄膜振动、热传导、扩散等过程的方程，具有非常重要的应用价值。

差分方法是一种常用的数值计算方法，用于求解微分方程，对于抛物型方程的数值求解也是非常有效的方法之一、本文将介绍抛物型方程的差分方法，并具体讨论用差分方法求解抛物型方程的一些具体问题。

首先，我们来介绍一下抛物型方程的一般形式。

抛物型方程一般可以表示为：∂u/∂t=α(∂^2u/∂x^2+∂^2u/∂y^2)其中，u(x,y,t)是待求函数，t是时间，x和y是空间变量，α是常数。

这个方程描述的是物理过程中的扩散现象，如热传导过程、溶质的扩散过程等。

差分方法的基本思想是将求解区域离散化为一个个网格点，然后在每个网格点处用近似的方式来计算待求函数的值。

差分方法的求解步骤主要包括以下几个方面：1.选择适当的网格和步长。

在求解抛物型方程时，需要确定空间变量x和y所在的网格点以及步长，同时也需要确定时间变量t所在的网格点和步长。

通常，我们会选择均匀网格，步长选择合适的值。

2.建立差分格式。

差分格式是差分方法的核心部分，它包括对方程进行近似处理和离散化。

对于抛物型方程，常用的差分格式有显式差分格式和隐式差分格式等。

其中，显式差分格式的计算速度快，但是有一定的稳定性限制，而隐式差分格式的稳定性较好，但是计算量较大。

因此，在具体问题中需要根据实际情况选择适当的差分格式。

3.编写计算程序。

在建立差分格式后，需要编写计算代码来求解离散方程。

具体编写的过程包括定义初始条件、建立迭代计算过程、以及计算结果的输出等。

4.计算结果的验证与分析。

求解方程后，需要对计算结果进行验证和分析，主要包括对数值解和解析解的比较、对误差的估计和控制等。

在具体求解抛物型方程时，还会遇到一些问题，例如边界条件的处理、稳定性和收敛性的分析等。

下面将对其中一些问题进行详细讨论。

1.边界条件的处理。

边界条件对差分格式的求解结果有着重要的影响，常见的边界条件包括固定端（Dirichlet）边界条件和自由端（Neumann）边界条件等。

10_抛物型方程的有限差分方法抛物型方程是一类常见的偏微分方程，广泛应用于自然科学和工程学的领域中。

有限差分方法是一种常用的数值求解抛物型方程的方法之一、本文将介绍抛物型方程的有限差分方法（II）。

有限差分方法主要基于离散化的思想，将偏微分方程转化为差分方程，进而求解差分方程的数值解。

对于抛物型方程，其一般形式可以表示为：∂u/∂t=Δu+f(x,t)其中，u(x, t)是未知函数，表示空间位置x和时间t上的解，Δu表示Laplace算子作用于u的结果，f(x, t)是已知函数。

有限差分方法的基本思想是将空间和时间域进行离散化，将连续的空间和时间划分为有限个网格点，然后使用差分近似代替偏导数，得到差分方程。

假设空间域被划分为Nx个网格点，时间域被划分为Nt个网格点，对于每个网格点(i,j)，可以表示为(x_i,t_j)，其中i=0,1,...,Nx，j=0,1,...,Nt。

在有限差分方法中，我们使用中心差分近似来代替偏导数。

对于时间导数，可以使用向前差分或向后差分，这里我们使用向前差分，即：∂u/∂t≈(u_i,j+1-u_i,j)/Δt对于空间导数，可以使用中心差分，即：∂^2u/∂x^2≈(u_i-1,j-2u_i,j+u_i+1,j)/Δx^2将上述差分近似代入抛物型方程中，可以得到差分方程的离散形式：(u_i,j+1-u_i,j)/Δt=(u_i-1,j-2u_i,j+u_i+1,j)/Δx^2+f_i,j其中，f_i,j=f(x_i,t_j)。

重排上式，可以得到递推关系式：u_i,j+1=αu_i-1,j+(1-2α)u_i,j+αu_i+1,j+Δt*f_i,j其中，α=Δt/Δx^2通过设置初始条件和边界条件，可以利用以上递推关系式得到抛物型方程的数值解。

总结来说，抛物型方程的有限差分方法（II）是一种常用的数值求解抛物型方程的方法。

它基于离散化的思想，将偏微分方程转化为差分方程，然后利用中心差分近似代替偏导数，得到差分方程的离散形式。

二维抛物方程的有限差分法二维抛物方程的有限差分法摘要二维抛物方程是一类有广泛应用的偏微分方程，由于大部分抛物方程都难以求得解析解，故考虑采用数值方法求解。

有限差分法是最简单又极为重要的解微分方程的数值方法。

本文介绍了二维抛物方程的有限差分法。

首先，简单介绍了抛物方程的应用背景，解抛物方程的常见数值方法，有限差分法的产生背景和发展应用。

讨论了抛物方程的有限差分法建立的基础，并介绍了有限差分方法的收敛性和稳定性。

其次，介绍了几种常用的差分格式，有古典显式格式、古典隐式格式、Crank-Nicolson隐式格式、Douglas差分格式、加权六点隐式格式、交替方向隐式格式等，重点介绍了古典显式格式和交替方向隐式格式。

进行了格式的推导，分析了格式的收敛性、稳定性。

并以热传导方程为数值算例，运用差分方法求解。

通过数值算例，得出古典显式格式计算起来较简单，但稳定性条件较苛刻；而交替方向隐式格式无条件稳定。

关键词：二维抛物方程；有限差分法；古典显式格式；交替方向隐式格式FINITE DIFFERENCE METHOD FORTWO-DIMENSIONAL PARABOLICEQUATIONAbstractTwo-dimensional parabolic equation is a widely used class of partial differential equations. Because this kind of equation is so complex, we consider numerical methods instead of obtaining analytical solutions. finite difference method is the most simple and extremely important numerical methods for differential equations. The paper introduces the finite difference method for two-dimensional parabolic equation.Firstly, this paper introduces the background and common numerical methods for Parabolic Equation, Background and development of applications. Discusses the basement for the establishment of the finite difference method for parabolic equation And describes the convergence and stability for finite difference method.Secondly, Introduces some of the more common simple differential format,for example, the classical explicit scheme, the classical implicit scheme, Crank-Nicolson implicit scheme, Douglas difference scheme, weighted six implicit scheme and the alternating direction implicit format. The paper focuses on the classical explicit scheme and the alternating direction implicit format. The paper takes discusses the derivation convergence,and stability of the format . The paper takes And the heat conduction equation for the numerical example, using the differential method to solve. Through numerical examples, the classical explicit scheme is relatively simple for calculation, with more stringent stability conditions; and alternating direction implicit scheme is unconditionally stable.Keywords:Two-dimensional Parabolic Equation; Finite-Difference Method; Eclassical Explicit Scheme; Alternating Direction Implicit Scheme1绪论1.1课题背景抛物方程是一类特殊的偏微分方程，二维抛物方程的一般形式为u Lu t ∂=∂ (1-1)其中1212((,,))((,,))(,,)(,,)(,,)u u u u u u L a x y t a x y t b x y t b x y t C x y t x x y y x y∂∂∂∂∂∂=++++∂∂∂∂∂∂ 120,0,0a a C >>≥。

抛物型方程有限差分法显—隐格式比较分析杨建宏【摘要】比较分析了抛物型偏微分方程有限差分法的显—隐两种基本格式,发现显格式计算简单、快捷,但格式条件稳定；隐格式计算复杂、工作量大,而格式却绝对稳定.对一维抛物型方程进行了数值求解,数值结果进一步证明了上述结论.%In this article, explicit and implicit schemes of the parabolic equation finite difference method is compared. It is discoveried that the explicit scheme calculate simply and quickly, but its scheme conditionally stable; the implicit scheme calculate complexly and its work load is big, but its scheme absolutely stable.【期刊名称】《河南科学》【年(卷),期】2012(030)004【总页数】4页(P407-410)【关键词】抛物型方程;有限差分法;显格式;隐格式【作者】杨建宏【作者单位】宝鸡文理学院数学系,陕西宝鸡721013【正文语种】中文【中图分类】O241.1抛物型方程描述了自然界和工程领域中许多重要的客观现象，要认识和掌握其规律就必须对它们进行精细的数值计算.有限差分法[1-5]（Finite Difference Method，简称FDM）是偏微分方程数值计算常用且理论比较成熟完善的方法之一，是计算机数值模拟最早采用的方法，至今仍被广泛运用.有限差分法在数值计算中占重要的地位，它的差分格式丰富多样，熟练掌握并能灵活运用这些格式直接决定着对问题的求解程度.本文从最基本的显格式和隐格式入手，以一维抛物型方程为例，对显、隐格式的计算效率和稳定性两个方面进行了比较分析，得到了它们各自的优缺点.算例结果进一步表明：显格式条件稳定，计算高效；隐格式绝对稳定，但算法复杂，工作量较大.最简单的一维抛物型方程是一维热传导方程以下在导出差分方程时，总是假设方程（1）式的解充分光滑.下面对方程（1）式直接用差分方法进行离散，用适当的差商代替方程中的偏微商，就得到以下两种最简单差分格式.1.1 显式差分格式在结点（ j，n）上用 u（xj，tn）在 t方向的向前差商和在x方向的二阶中心差商似代替方程（1）中的偏导数，得以r=τ/h2表示网格步长比，（2）式即为其中0≤n≤N=［T/τ］，j∈Z.格式（3）式通常称为方程（1）式的古典显式差分格式.1.2 隐式差分格式格式（5）通常称为方程（1）的古典隐式差分格式.2.1 计算效率比较显格式（3）中不同时间层网格结点间关系如图1所示.可见第n+1时间层上任一网格结点xj=jh处的差分解unj+1完全由第n时间层上三个相邻结点xj±1和xj处的初值｛unj±1 ，ujn｝决定，因此采用显式差分格式计算时，逐层递推上一层，计算简便快捷.隐格式（5）中不同时间层网格结点间关系如图2所示.可见ujn+1的计算需要用到unj±+11的值，而它们也是未知数，也就是说，方程（5）仅仅给出ujn+1所满足的方程，通常需要求解它与初边值条件耦合形成的代数方程组.所以用隐式差分格式进行计算时，计算复杂，计算量较大.2.2 稳定性比较显格式（3）是条件稳定的[2-3]，其稳定条件为r=τ/h2≤1/2.这要求在运用此格式时一定要注意网格比例，如果不满足稳定性条件，计算结果将会失真.而且要求时间步长尽量小，当空间维数越高时，时间步长要越小.隐格式（5）是绝对稳定的[2-5]，对网格比没有任何限制，因此利用它进行数值计算时，可以将r取得大一些，以减少时间步数，但是每一个时间层都需要解线性代数方程组，计算复杂，计算量很大.为了进一步证明上述结论的正确性，考虑满足如下初边值条件的一维热传导方程. 在t=0.5时，分别用有限差分法显，隐格式求解方程（6）式.方程（6）式的解析解为 u（x，t）=e－π2tsin（πx）.取空间步长 h=0.1，r=τ/h2＝0.05 和 1，即时间步长τ分别取为 0.000 5 和 0.01.方程（6）式的显格式如下取 h=0.1，取r=τ/h2＝1，即τ取为 0.01.方程（6）式的隐格式如下在表1和图3中给出了t=0.5时，方程（6）式的有限差分显格式在步长比r分别为0.05和1时，不同节点处的数值解和方程精确解的比较.1000=│u（xj，0.5）-uj1000│为绝对误差.在表2和图4中给出了t=0.5时，方程（6）的有限差分隐格式在步长比r为1时不同节点处的数值解和方程精确解的比较.其中：uj1000（r=0.05）表示r=0.05时的数值解，uj50（r=1）表示r=1时的数值解，u（xj，0.5）为精确解，εj其中：uj50（1）表示用古典隐格式计算出的在 t=0.5 时的数值解，u（xj，0.5）为精确解，εj50（1）为它与精确解的绝对误差.由表1和图3可见，r=0.05时的数值解逼近方程的精确解，而r=1时的数值解却严重失真.表明有限差分显格式是条件稳定的.由表2和图4可见，当r=1时，有限差分隐格式的数值解逼近方程的精确解，表明隐格式是绝对稳定的.而且，进一步发现显格式的计算精度优于隐格式.当然，可通过减小时间步长和加大迭代次数来提高隐格式的计算精度.本文对抛物型偏微分方程有限差分方法显，隐两种格式进行了比较分析.发现，显格式条件稳定，计算高效、快捷；隐格式绝对稳定，但计算复杂、工作量大.【相关文献】［1］余德浩，汤华中.微分方程数值解法［M］.北京：科学出版社，2003.［2］李荣华.偏微分方程数值解法［M］.北京：高等教育出版社，2005.［3］李瑞遐，何志庆.微分方程数值解法［M］.上海：华东理工大学出版社，2005.［4］南京大学数学系计算数学专业.偏微分方程数值解法［M］.北京：科学出版社，1979. ［5］孙志忠.偏微分方程数值解法［M］.北京：科学出版社，2005.。

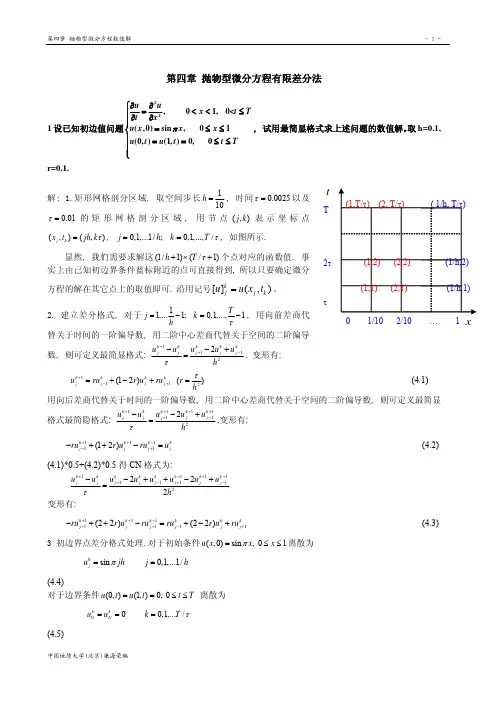
第四章 抛物型微分方程有限差分法1设已知初边值问题22, 01, 0<(,0)sin , 01(0,)(1,)0, 0 u ux t t x u x x x u t u t t T π⎧∂∂=<<⎪∂∂⎪⎪=≤≤⎨⎪==≤≤⎪⎪⎩T ≤, 试用最简显格式求上述问题的数值解。

取h=0.1,r=0.1.0 1/10 2/10 … 1 T 2τ τt解: 1.矩形网格剖分区域. 取空间步长1, 时间2510h =0.00τ=以及0.01τ=的矩形网格剖分区域, 用节点)表示坐标点(,j k (,)(,)j k x t jh k τ=, 0,1,...1/; 0,1,...,/j h k T τ==, 如图所示.显然, 我们需要求解这(1/1)(/1)h T τ+×+个点对应的函数值. 事实上由已知初边界条件蓝标附近的点可直接得到, 所以只要确定微分方程的解在其它点上的取值即可. 沿用记号[]k(,)j j k u x t =。

u 2. 建立差分格式, 对于11,...1; 0,1,...,1Tj k hτ=−=−, 用向前差商代替关于时间的一阶偏导数, 用二阶中心差商代替关于空间的二阶偏导数, 则可定义最简显格式:1122k k k k k1jj j j u u u u u h ++−+=. 变形j τ−−有:1112(12) (k k k kj j j j u ru r u ru r h τ+−+=+−+=(4.1)用向后差商代替关于时间的一阶偏导数, 用二阶中心差商代替关于空间的二阶偏导数, 则可定义最简显格式最简隐格式:111122k k k k k j jj j j u u u u u h τ++++−−+=11+−1kj +,变形有:1111(12) k k k j j j ru r u ru u ++−−−++−= (4.2)(4.1)*0.5+(4.2)*0.5得CN 格式为:111112222k k k k k k k k j jj j j j j j u u u u u u u u h τ+++−+−−++−+=111++−1kj +x x变形有:111111(22)(22) k k k k k j j j j j ru r u ru ru r u ru ++−−+−−++−=+−+ (4.3)3 初边界点差分格式处理.对于初始条件u x (,0)sin , 01=π≤≤h 离散为(4.4)0sin 0,1,...1/j u jh j π==对于边界条件离散为(0,)(1,)0, 0 u t u t t T ==≤≤00 0,1,.../k k N u u k T τ===(4.5)总结: 联立方程(4.1)(4.4)(4.5)得到已知问题的最简显格式差分方程组:11100(12)1 1,...1; 0,1,...,1sin 0,1,...1/0 0,1,.../k k k k j j j j jk k N u ru r u ru T j k h u jh j h u u k T τπτ+−+⎧=+−+⎪⎪=−=−⎪⎨⎪==⎪⎪===⎩ 联立方程(4.2)( 4.4)( 4.5)得到已知问题的最简隐格式差分方程组:1111100(12) 1 1,...1; 0,1,...,1sin 0,1,...1/0 0,1,.../k k k k j j j j jk k N ru r u ru u T j k h u jh j h u u k T τπτ++−−+⎧−++−=⎪⎪=−=−⎪⎨⎪==⎪⎪===⎩ 联立方程(4.3)( 4.4)( 4.5)得到已知问题的CN 格式差分方程组:11111100(22)(22) 1 1,...1; 0,1,...,1sin 0,1,...1/0 0,1,.../k k k k k j j j j j jk k N ru r u ru ru r u ru T j k h u jh j h u u k T τπτ++−−+−⎧−++−=+−+⎪⎪=−=−⎪⎨⎪==⎪⎪===⎩1k j + 4 求解并显示结果利用软件计算(Matlab)如上最简显格式差分方程组.h=1/10;tau=0.0025;T=0.5; r=tau/h^2;M=1/h+1;N=T/tau+1; u=zeros(M,N);for m=1:Mu(m,1)=sin((m-1)*h*pi); endu(1,1:N)=0;u(M,1:N)=0;for n=1:N-1for m=2:M-1u(m,n+1)=r*(u(m+1,n)+u(m-1,n))+(1-2*r)*u(m,n); end end u=u’ 这样我们就计算出不同时刻不同位置k t j x 对应的函数值(,)j k u x t 取tau=0.0025, 即r=0.25绘图, 取tau=0.01, r=1再绘图,如图()图4.2 习题1数值解图示(左r=0.25, 右r=1)2.试构造初边值问题 ()()()()(), 0.51, 0,,0, 0.51,0.5,0, 1,0.51,, 0u u x x x T t x x u x x x u ⎪∂u t t u t t T x ϕ⎧∂∂∂⎛⎞=<<<≤⎜⎟⎪∂∂∂⎝⎠⎪⎪=≤≤⎨⎪==−≤≤⎪∂⎩的显格式，并给出其按最大范数稳定的充分条件。

分类号：O241.82本科生毕业论文（设计）题目：一类抛物型方程的计算方法作者单位数学与信息科学学院作者姓名专业班级2011级数学与应用数学创新2班指导教师论文完成时间二〇一五年四月一类抛物型方程的数值计算方法(数学与信息科学学院数学与应用数学专业2011级创新2班）指导教师摘要: 抛物型方程数值求解常用方法有差分方法、有限元方法等。

差分方法是一种对方程直接进行离散化后得到的差分计算格式，有限元方法是基于抛物型方程的变分形式给出的数值计算格式。

本文首先给出抛物型方程的差分计算方法，并分析了相应差分格式的收敛性、稳定性等基本理论问题.然后，给出抛物型方程的有限元计算方法及理论分析。

关键词：差分方法，有限元方法，收敛性，稳定性Numerical computation methods for a parabolic equationYan qian（Class 2, Grade 2011，College of Mathematics and Information Science）Advisor: Nie huaAbstract：The common methods to solve parabolic equations include differential method，finite element method etc。

The main idea of differential method is to construct differential schemes by discretizing differential equations directly. Finite element scheme is based on the variational method of parabolic equations。

In this article, we give some differential schemes for a parabolic equation and analyze their convergence and stability. Moreover，the finite element method and the corresponding theoretical analysis for parabolic equation are established.Key words：differential method，finite element method, convergence，stability1 绪 论1。

基于matlab解抛物型方程的交替隐方向p-r差分格式的实现1. 引言1.1 概述本文旨在利用MATLAB中的抛物型方程解析方法，具体实现交替隐方向p-r差分格式。

抛物型方程是一类常见的偏微分方程，在科学计算和工程领域中有着广泛的应用。

该类方程描述了许多自然界和社会系统中的动态过程，如热传导、扩散、弹性形变等。

而交替隐方向p-r差分格式则是一种高效解法，适用于求解抛物型方程。

1.2 文章结构本文将按以下结构展开详细论述：- 第2节将简要介绍抛物型方程及其解析方法概述，并特别关注MATLAB在此过程中的应用。

- 第3节将深入探讨交替隐方向p-r差分格式的原理，并对其稳定性和精确度进行分析。

- 第4节将重点阐述基于MATLAB实现交替隐方向p-r差分格式的步骤，包括空间离散化方法选择与实现、时间离散化方法选择与实现、以及迭代求解过程描述与收敛性分析。

- 最后，第5节将呈现数值实验设置，并展示数值结果，同时对结果进行讨论。

1.3 目的本文的目的在于通过MATLAB解析抛物型方程，并实现交替隐方向p-r差分格式，从而提供一种高效、稳定、精确的数值计算方法。

此研究对于处理抛物型方程相关问题具有实际应用意义，为科学计算和工程领域中的相关研究提供了指导和借鉴。

我们期望该研究能够拓展数值计算方面的知识，促进在实践中解决复杂系统动态过程模拟与分析的能力。

2. 抛物型方程解析2.1 抛物型方程简介抛物型方程是一类常见的偏微分方程，它描述了许多自然现象和数学模型中的动态行为。

一般而言，抛物型方程包括一个时间变量和多个空间变量，并且通常具有二阶时间导数和二阶或更高阶的空间导数。

典型的抛物型方程包括热传导方程、扩散方程和波动方程等。

2.2 解析方法概述解析方法是指通过使用数学分析和解析推导来求解偏微分方程的方法。

在抛物型方程的解析研究中，常用的方法包括变量分离法、相似变量法、格林函数法等。

这些方法基于物理建模和数学推导，可以得到精确的解或者近似解。