当前位置：文档之家 › 13年力学竞赛辅导理论力学3

13年力学竞赛辅导理论力学3

  • 格式：ppt
  • 大小：1.17 MB
  • 文档页数：29

下载文档原格式

  / 29

合集下载

15年力学竞赛辅导理论力学(1)解析

15年力学竞赛辅导理论力学(1)解析


(3) 掌握点的复合运动的基本概念，掌握并能应用点的速度合成定理和
加速度合成定理。 (4) 掌握刚体平面运动的概念及其描述，掌握平面运动刚体速度瞬心的
概念。能熟练求解平面运动刚体的角速度与角加速度以及刚体上各点的
速度和加速度。
7
ห้องสมุดไป่ตู้
(三)动力学 (1) 掌握建立质点的运动微分方程的方法。了解两类动力学基本问题的 求解方法。 (2) 掌握刚体转动惯量的计算。了解刚体惯性积和惯性主轴的概念。 (3) 能熟练计算质点系与刚体的动量、动量矩和动能；并能熟练计算力 的冲量（矩），力的功和势能。 (4) 掌握动力学普遍定理(包括动量定理、质心运动定理、对固定点和质 心的动量矩定理、动能定理)及相应的守恒定理，并会综合应用。 (5) 掌握建立刚体平面运动动力学方程的方法。了解其两类动力学基本 问题的求解方法。 (6) 掌握达朗贝尔惯性力的概念，掌握平面运动刚体达朗贝尔惯性力系 的简化。掌握质点系达朗贝尔原理(动静法) ，并会综合应用。了解定轴 转动刚体静平衡与动平衡的概念。
(一) 静力学 (1) 掌握力、力矩和力系的基本概念及其性质。能熟练地计算力的投影、力 对点的矩和力对轴的矩。 (2) 掌握力偶、力偶矩和力偶系的基本概念及其性质。能熟练地计算力偶矩 及其投影。 (3) 掌握力系的主矢和主矩的基本概念及其性质。掌握汇交力系、平行力系 与一般力系的简化方法、熟悉简化结果。能熟练地计算各类力系的主矢和 主矩。掌握重心的概念及其位置计算的方法。
1
2
全国周培源大学生力学竞赛
简介 上世纪八十年代的中国，百废待兴，科学技术的发展优甚, 培养下一代高 素质的人才是时代的呼唤。全国大学生力学竞赛就是在这样的背景下开始 酝酿的。 1986年8月在呼和浩特市召开的《力学与实践》编委会上，北京大学武 际可教授(现为全国周培源大学生力学竞赛组委会顾问)建议举办大学程度 的力学竞赛，获得一致赞同。中国力学学会理事长郑哲敏院士听取了有关 工作汇报并安排《力学与实践》编委会筹办。尔后,国内众多的力学名家积 极参与了此事.包括赞助、命题、评选等. 为了鼓励青年学生学习老一辈科学家为科学的献身精神，这项竞赛从 1996年第三届起改名为“全国周培源大学生力学竞赛”。 根据首届竞赛的反馈意见，为了吸引更多的学生参赛，竞赛内容精简为只 含理论力学和材料力学两门工科学生普遍学习的课程；为了保证平等竞争， 采用了闭卷方式，在全国各考点同一时间用统一试卷竞赛。这一措施收到了 很好的效果，
理论力学竞赛指导-PPT课件

理论力学竞赛指导-PPT课件

2 k 2 0 x ( )x m
当 2

2k m
牵连惯性力大于弹簧的弹性恢复力，
物块不能在x´＝0处附近作自由振动，物块在x´＝0处 的平衡是不稳定的。 当
2
2k m
牵连惯性力等于弹簧的弹性恢复力
物块在x´＝0处为随遇的平衡位置。
4、水流以体积流量qV通过内径为d1管
z
ω
北
解：3. 分析加速度
绝对加速度aa －所要求的 未知量；
z´ ae ar
vr
相对加速度ar － ar=vr2/R 方向指向地心；
牵连加速度ae － ae=Rcos2ae 矢量垂直于 Oz´轴，方向指向Oz´； 科氏加速度aC － aC=2vrsin方向沿过P点纬 线的切向，指向西。
aC
k
P O
k
y´
k x´
解： 1. 非惯性参考系－O x´ y´ 动点－物块P 2. 分析相对速度和各种加速 度： 相对速度vr －沿着x´正向
OP kk
P x´

aIC
牵连加速度aen－由大盘 转动引起
vr
aen
科氏加速度aIC －2m vr
y´ k x´ 解： 3. 分析质点(物块)受力： F －弹簧力F＝2k x´ FIC aIC vr aen F FN －槽对物块的约束力 FIC －科氏力 FIen －法向牵连惯性力 FIen＝m 2 x´
1
qv
1
2
2
解：分析以喷嘴的左右截面(1－1 和2－2)为边界所包含的质量流根据 体积流量与速度和管道横截面积的 关系，有
2 2 π d π d q v A v A v 1 v 2 V 1 1 2 2 1 2 4 4
理论力学第三章 刚体力学-3

理论力学第三章 刚体力学-3


I
zx
I zy
I zz
**
(2)惯量椭球－用几何方法求刚体对某瞬时轴的转动惯量
Q点的坐标为：
x R
y
R
z
l
Q
R x
R y
z R 代入**得
y
o
x
椭球面方程
R z
Ixx x2 Iyy y2 Izz z2 2Iyz yz 2Izxzx 2Ixy xy 1
中心惯量椭球：刚体的质心(或重心)在O点
刚体绕基点A的“定点”转动，则刚体上任一点P的速度为
A
r
加速度为
a
aA
d
dt
r
(
r)
r是P点相对于基点A的位矢
3、刚体绕两相交轴转动的合成
刚体绕某点O作定点转动，相当于刚体绕某轴作“定轴”
转动，而该轴又绕另一固定轴转动，这两个轴相交于O点。
z
2
•
1
x
o
y
结论：当刚体绕两个相交轴转动时，刚体的瞬时角速 度等于它分别绕这两个轴转动的角速度的矢量和。
Izx
I xy I yy I zy
I I
xz yz
x y
Izz z
三、转动惯量
转动惯量：描述刚体转动惯性大小的物理量。 1、对定轴转动惯性的大小用转动惯量描述， 其定义为：
I midi2 或 I d 2dm
即转动惯量=各质点的质量与该点到转轴距离平方乘积之 和。转动惯量由刚体的质量分布和转轴位置决定。
i 1
ri
xii
xi
yi j
y
zik
j zk
J J
x y
I xx I yx
I xy I yy
理论力学03

理论力学03


理论力学CAI
21
2013年12月6日理论力学CAI22固定铰链支座
2013年12月6日
理论力学CAI
23
2013年12月6日
理论力学CAI
24
二力杆约束
两端用球铰或平面柱铰与其他物体联结且不计重量的 刚性直杆称为二力杆
•二力杆可承受拉力和压力 •二力杆内力处处相等
2013年12月6日
理论力学CAI
2013年12月6日
理论力学CAI
9
2013年12月6日
理论力学CAI
10
圆柱铰链
2013年12月6日
理论力学CAI
11
2013年12月6日
理论力学CAI
12
平面柱铰
2013年12月6日
理论力学CAI
13
空间柱铰
Mz
Fz
My Fy Fx
2013年12月6日
理论力学CAI
14
滚动轴承和推力角轴承
理论力学CAI
34
画出下列各构件的受力图
2013年12月6日
理论力学CAI
35
画出下列各构件的受力图
2013年12月6日
理论力学CAI
36
2013年12月6日
理论力学CAI
37
画出下列各构件的受力图
2013年12月6日
理论力学CAI
38
画受力图应注意的问题
1、不要漏画力
除重力、电磁力外，物体之间只有通过接触才有 相互作用力，要分清研究对象与周围哪些物体相接触 ，接触处必有力，力的方向由约束类型而定。
25
固定端约束
2013年12月6日
理论力学CAI
26
理论力学-c3-3

理论力学-c3-3

= ⋅ Ԧ =
2
3
➢ 若正方体绕对角线运动， =
Ԧ =
2
6 3
Ԧ + Ԧ + ,

3
Ԧ + Ԧ + ，则
1
2 2
= ⋅ Ԧ =
2
12
12
平行轴定理
转轴, 平行，距离为。刚体绕穿过质心的轴转动惯量为 ，则
绕轴的转动惯量为
= + 2
（1）啤酒瓶（2）你和镜中人（3）四门塔
22
小结
定点运动，刚体角动量和动能
Ԧ = መ ⋅ ,
1
= ⋅ መ ⋅
2
若取惯量主轴为坐标轴，则
1
መ = 0
0
Ԧ = 1 Ԧ + 2 Ԧ + 3 ,
0
2
0
0
0
3
1
= 1 2 + 2 2 + 3 2
1
2 ,
6
= = 0
2 Τ6
0
0
2

መ =
=

0
2 Τ6
0
6
2
0
0
Τ6
9
2
መ =

6

上式中为单位矩阵，满足
⋅ =
角动量为
2
Ԧ = መ ⋅ =

6



动能为
1
2 2
= ⋅ Ԧ =

2
12
正方体绕质心的角动量与角速度同方向，动能正比于角速度大小
′
−
−
−

′
−
′
理论力学第三章

理论力学第三章


M
F'
F
二、空间力偶等效定理
空间力偶的等效条件是：作用在同一刚体上的两个力偶， 如果力偶矩矢相等，则两力偶等效。
理论力学 中南大学土木工程学院 24
理论力学
中南大学土木工程学院
25
理论力学
中南大学土木工程学院
26
三、空间力偶系的合成与平衡
1、合成
力偶作用面不在同一平面内的力偶系称为空间力偶系。 空间力偶系合成的最后结果为一个合力偶，合力偶 矩矢等于各分力偶矩矢的矢量和。即：
8
[例]图示起重机吊起重物。起重杆的A端用球铰链固定在地面上，B端用 绳CB和DB拉住，两绳分别系在墙上的C点和D点，连线CD平行于x轴。 已知CE=EB=DE，角a =30o ，CDB平面与水平面间的夹角∠EBF= 30o， 重物G=10kN。如不计起重杆的重量，求起重杆所受的力和绳子的拉力。 解：1、取杆AB与重物为研究 对象，受力分析如图。
空间力系向点O简化得到一空间汇交力系和一空间 力偶系，如图。
z O
F1 y F2 z M2 z F'1 Mn F'2 y
Fn x
＝
M1 x
O F'n
＝
MO
F'R
O y
x
( i 1，， 2 ，n )
Fi Fi M i M O ( Fi ) ri Fi
M M cos( M，k ) z M
27
理论力学
中南大学土木工程学院
[例]工件如图所示，它的四个面上同时钻五个孔，每个孔所受的切削力偶 矩均为80N· m。求工件所受合力偶的矩在x，y，z轴上的投影Mx，My，Mz， 并求合力偶矩矢的大小和方向。
13理论力学讲义第十三讲PPT课件

13理论力学讲义第十三讲PPT课件


证明：相同的速度和加速度?
A1
z
rArBBA
rA A
drA drB dBA dt dt dt
vAvB aAaB
O
rB B
x
退出
结论：刚体平动的问题，可归结为点的运动问题
B1
y
§8－1 刚体的平行移动
7
7 例8-1：曲柄滑块机构中，当曲柄OA在平面上绕定轴O转动时
，通过滑槽连杆中的滑块A的带动，可使连杆在水平槽中沿直 线往复滑动。若曲柄OA的半径为r，曲柄与x轴的夹角为ф=ωt ，其中ω是常数，求此连杆在任一瞬时的速度及加速度。
d
dt
d d dt d
/2
d d
an
0
0
an r
a r
a a2an2 a
ωα
a a2an2r12
arcatgarc1tg1.77
an
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
退出
ωα at
aθ
an
φ
x
O
§8－3 转动刚体内各点的速度与加速度
例如：转动刚体从静止开始，以匀角加速度α逆时针转动，分析角位移
为0。90。时OM线上的切向加速度、法向加速度和全加速度的分布
O
at=xa
Mo
α
a 0。时OM线上at、an和a的分布: t
vr0
an r2 0
M
a r an r2 ?
9 9
转动的度量： φ=φ（t） 刚体的定轴转动方程
φ角位移
y
13年力学竞赛辅导理论力学3

13年力学竞赛辅导理论力学3


而
aA vA
vt
2
h
3 2 2

17
例2. 某一点的运动轨迹为平面曲线, 其速度在铅垂方向的投影始终是常量C. 求证: 任意时刻点的加速度大小 为:
v3 a C 其中, 为点所在曲线处的曲率 半径
证明: 不妨设铅垂轴为 轴 x 则 Vx C ax 0
18
又
v2 an ρ

取长方块B 分析
Y
i
0:
FN W cos300 F2 si n350 0
FN 107 20 N .
F1
W
F2
F
B
30º
X
P
W
x
i
0:
F2 cos350 F W si n300 P 0 F FN tg350 75.06 N
P 4.34 N
Q W a P W g
b
C
Q
a
hmin
A
W
FS
B
P
b c mB 0 : Q W P hmin 0 2 2
hmin 1 Q b W c b W b c 2P 2 2P
FN
令上式中hmin = 0 若hmin > 0
14
合成法( 瞬时法):(1) 已知运动的点与未知的点在同一刚体上 刚体平面运动
基点法, VB VA VBA ( 包括速度投影及速度瞬心法)
n t a B a A a BA a BA
(2) 已知运动 的刚体(或点)和未知的刚体(或点)之间的相对运动— 点的合成运动.
Va Ve Vr
13年力学竞赛辅导理论力学4

13年力学竞赛辅导理论力学4


30º
O1
将 a a a a a a e r C沿 C 方向投影
n 0 a cos 30 a a a C e
a 3 2 e rad /s a 200 3 100 3 100 3 mm / s O A 2 1 2 n 0 n a 50 200 150 mm / s 将 a a a a 沿 A B 方向投影 : a sin 30 a a r a e r C a e r
A 点与B 点相对于CO1 的速度相等 ( 平动 )
V V 100 3 mm / s B r r
而 V O B 50 mm / s B 1 e
2 2 V V V 180 . 28 mm / s B B B e r
4
取活塞杆的A点 为动点, 汽缸CO1 为动系加速度分析如图示
a 2 V k CD r
3 2 r 2
V
e
30º
V
由
r
e
n n 沿 a k 方向投影: a a a a a a e e r k
n 0 a cos 30 a a a e k
a 2 e 3 CD BC
V
a
a a cos 30 a 3 r k
注意上式在这里不仅是瞬时成立!
a d dV (C ) C dt dt r r
B

a

C
n c
V
C
a C
以C 为基点, A 点的加速度分析如图
2 2 V V C C n n 2 a a r C AC R r r a r a C AC
a a
B
理论力学3分析力学基础课后答案

理论力学3分析力学基础课后答案


代入拉格朗日方程，得
则 3-3
[
]
质量为 m 的质点悬在 1 线上，线的另 1 端绕在 1 半径为 R 的固定圆柱体上，如图
250
3-3 所示。设在平衡位置时，线的下垂部分长度为 l，且不计线的 质量。求此摆的运动微分方程。 解 取 θ 为广义坐标，设小球的静平衡位置为其零势能点。 系统势能
V = mg [(l + R sin θ ) − (l + θR ) cosθ ]
A
A x
& & x
θ
C
θ
FN
ϕ
θ −ϕ
l & ϕ 2 y
θ
& & x
θ
x′ B
C mg B
(c)
l && ϕ 2 y
(a)
& （见图 3-7b） & 、ϕ 解 2 自由度，给广义坐标 x， ϕ ，则广义速度为 x
(b) 图 3-7
l & & − cos(θ − ϕ )ϕ vCx = x 2 l & sin(θ − ϕ ) vCy = ϕ 2
x A = x B = 0, y A = −2a sin θ ， y B = 2a sin θ , xO = 2a cosθ
对相应坐标的变分
δ x A = δ x B = 0,δ y A = −2a cosθδ θ ,δ y B = 2a cosθδ θ δ xO = −2a sin θδ θ
根据动力学普遍方程，有
系统动能
势能
m 2 m 2 l2 2 m 1 m 2 & 2 = (x & + ϕ & − lx &ϕ & cos(θ − ϕ )) + l 2ϕ &2 (vCx + vCy ) + ⋅ l 2ϕ 2 2 12 2 4 24 m 2 m 2 2 m & + lϕ & − lx &ϕ & cos(θ − ϕ ) = x 2 6 2 l V = − mgx sin θ − mg cos ϕ （设初始 A 处势能为零） 2 T= ∂L m & cos(θ − ϕ ) & − lϕ = mx & ∂x 2 d ∂L m m && cos(θ − ϕ ) − lϕ & sin(θ − ϕ )ϕ & & − lϕ ( ) = m& x & dt ∂x 2 2
2013力学竞赛个人赛题目解答

2013力学竞赛个人赛题目解答


置，以防止其在轴向上产生位移。两组金属片下方均与 O′ 处的轴套铰结，该轴套与轴 OO′ 光滑套
合。当主机上的电动机带动两组金属片旋转时，O′ 处的
轴套会向上升起。但轴套上升时，会使沿轴安装的弹簧 压缩。弹簧的自然长度为 2L ，其刚度 k = 23G 。O 和 O′
L 处的轴套、弹簧，以及各处铰的重量均可以忽略。
A
O
q1 / 2 A
(c)
可以一般性地假设，在如同图 1-4(a) 那样荷载呈线性分布的简支梁中，A 处的转角为 ξ q1L3 ， EI
其中 ξ 是一个待定的无量纲常数。图 1-4(a) 的荷载可分解为对称部分和反对称部分之和，分别如图
1-4(b) 和图 1-4(c) 所示。在图 1-4(b) 中，A 处转角为 ⎜⎛ q1 ⎟⎞ L3 = q1L3 。在图 1-4(c) 中，由于荷载 ⎝ 2 ⎠ 24EI 48EI
。
④
同样，在下片中，如图 1-2(a)，由平衡方程可得
Yb
=
27 8
3
G
。
故弯矩方程为
Mb
=
−
75 3G 24L2
x3
−
3G x2 + 27 3G x ，
4L
8
上式同样可整理为
( ) M b =
3G 8L2
− 25x3 − 2Lx2 + 27L2 x 。
积分可得转角和挠度方程为
( ) θb
=
3G 96EIL2
详细参考解答及评分标准
评分总体原则 各题均不限制方法。若方法与本文不同，只要结果和主要步骤正确，即给全分；若方法不同而
结果不正确，各地自行统一酌情给分。本文中多处用图形解释，若试卷中未出现相应图形但已表达 了同样的意思，则同样给分。计算结果用分数或小数表达均可。

理论力学竞赛练习题答案

理论力学竞赛练习题一、基础概念题1. 列出牛顿运动定律的三个基本内容。

2. 简述质点与刚体的区别。

4. 解释力的合成与分解。

5. 简述功和能量的概念及其关系。

二、单选题A. 速度B. 力C. 加速度D. 质量2. 在自由落体运动中，物体的加速度为：A. 0B. 9.8 m/s²C. 5 m/s²D. 10 m/s²A. 惯性与物体的速度有关B. 惯性与物体的质量无关C. 惯性是物体保持静止状态的性质D. 惯性是物体保持匀速直线运动状态的性质三、计算题1. 一物体从静止开始沿直线加速运动，经过10秒后速度达到20 m/s，求物体的加速度。

2. 一质量为2 kg的物体在水平面上受到10 N的力作用，求物体的加速度。

3. 一物体从高度h自由落下，不计空气阻力，求物体落地时的速度。

4. 一物体沿半径为5 m的圆周运动，速度为10 m/s，求物体的向心加速度。

5. 一物体在水平面上受到两个力的作用，其中一个力为30 N，方向向东，另一个力为40 N，方向向北，求物体的合力。

四、应用题1. 一辆汽车以20 m/s的速度行驶，紧急刹车后，加速度为5m/s²，求汽车停止前行驶的距离。

2. 一物体在斜面上受到重力和摩擦力的作用，已知重力为30 N，摩擦力为10 N，求物体的合力。

3. 一质量为1 kg的物体在水平面上受到一个变力的作用，力随时间的变化关系为F=3t²（N），求物体在05秒内的位移。

4. 一物体在半径为10 m的圆形轨道上做匀速圆周运动，速度为5 m/s，求物体在1分钟内转过的角度。

5. 一质量为5 kg的物体在水平面上受到一个恒力的作用，力的大小为20 N，方向与初速度方向成30°角，求物体在5秒内的位移。

五、判断题1. 动能定理表明，物体的动能变化等于所受外力做的功。

（）2. 在圆周运动中，物体的速度方向始终沿着半径方向。

（）3. 作用力和反作用力大小相等，方向相反，作用在同一直线上。

理论力学竞赛辅导1静力学-




M l3 0
确定三根轴的位置
2019/11/13
26
BUAA
静力学的思考题与例题
思考题26：长正方体上作用有一空间任意力系，对 其中的六个轴取矩方程均成立，该力系是否是平衡 力系。
l3
MO
FR
l5
l6
o
l2
l3
MO
FR
l6 o
l1
l4
l1
{ F 1,F 2, ,F n} { F R ,M o}
i1
i1
空间任意力系的平衡条件：

FR

0


Fx 0

Fy 0 MO 0
MOx(F) 0
MOy(F) 0


M x(F ) 0 M y (F ) 0,
Fz 0


MOz(F) 0

M z(F ) 0
•静不定问题 ( statically indeterminate problem): 未知量的数目> 独立平衡方程的数目
注： 静不定的物理含义是系统存在有多余约束
静不定结构中，不一定是所有约束力均不能唯一确定
问题7：系统如图所示，已知滑块与地面之间的静/动摩擦因数 和几何尺寸，该系统处于平衡。试分析该系统的静定性。
C
CF
AM
B
A F
2019/11/13
n
Fi ri 0
i1
M B
F
F
19
BUAA
平衡位置的稳定性
设质点系的势能函数为：VV(q1,q2, ,qk)
质点系在势力场中的平衡充分必要条件是：

理论力学-c3-1


（2）再由 Ƹ ∥ Ƹ × Ƹ 确定 方向， 在ξηζ系中，
到轴转动的角度为（绕轴）
轴的极角 =
轴的方位角 =

−
2
17
z

例6：地球的欧拉角
y

O


x


春分日
夏至日

N
秋分日

：章动角，黄赤交角 常数
：进动角， = 常数

：自转角， = 0 +
为2 ，自转轴与竖直轴夹角, 求总角速度矢量
解答：（1）建立柱坐标系，自转角速度为
1 = 1 sin Ԧ + cos
（2）令1 = 0，显然柱系的Ԧ, Ԧ, 固定在陀螺上，他们
Ԧ
随着进动而改变方向，2 = 2
（3）令2 = 0，则陀螺不再转动
= 1 + 2 = 1 sin Ԧ + 2 + 1 cos
=
12 + 22 + 21 2 cos
11
例5：杆一端挂在横梁上点，绕悬挂点以Ω转动；另一端连接圆
盘。分析两种情况下圆盘的角速度。
（1）盘与杆保持垂直，圆盘绕杆以转动
（2）盘保持水平，圆盘绕竖直轴以转动
12
§3.3 欧拉角
➢ 对于单质点，空间位置 Ԧ → 速度矢量 Ԧሶ = Ԧ
Ԧ = 0 Ԧ,
Ԧ = 0 − Ԧ,
Ԧ = Ԧ + Ԧ
➢ 同样地，刚体转动，如何确定角速度？
确定刚体的所有分角速度1 , 2 , …，利用矢量加和得到
= 1 + 2 + ⋯
前提条件：角速度是矢量（略，详见本节ppt附录）

理论力学理论力学3 第三章


例3-1 已知： Fn , ,
求：力 F在n 三个坐标轴上的投影.
解： Fz Fn sin
Fxy Fn cos
Fx Fxy sin Fn cos sin
Fy Fxy cos Fn cos cos
二.空间汇交力系的合力与平衡条件
✓ 空间汇交力系的合力: FR Fi
✓ 合矢量（力）投影定理
✓ 空间汇交力系平衡的充分必要条件是：
该力系的合力等于零，即 FR 0
空间汇交力系 的平衡方程
Fx 0 Fy 0 Fz 0
空间汇交力系平衡的充要条件：该力系中所有各 力在三个坐标轴上的投影的代数和分别为零。
例3-2 已知：物重P=10kN，CE=EB=DE； 300
求：杆受力及绳拉力
FRx Fx
FRy Fy
FRz Fz
合力的大小 FR ( Fx )2 ( Fy )2 ( Fz )2
方向余弦
cos( FR
,i )
Fx FR
cos( FR
,
j)
Fy FR
cos( FR
,
k)
Fz FR
空间汇交力系的合力等于各分力的矢量和，合 力的作用线通过汇交点。
例3-6 已知：两圆盘半径均为200mm，AB =800mm，圆盘面O1垂直 于z轴，圆盘面O2垂直于x轴，两盘面上作用有力偶，F1=3N， F2=5N，构件自重不计. 求:轴承A,B处的约束力.
第三章 空间力系
✓ 空间力系的简化 ✓ 空间力系的平衡
§3–1 空间汇交力系
空间汇交力系:
空间力系中各力作用线汇交于一点。
一.力在直角坐标轴上的投影
直接投影法
Fx F cos
Fy F cos Fz F cos

理论力学3章

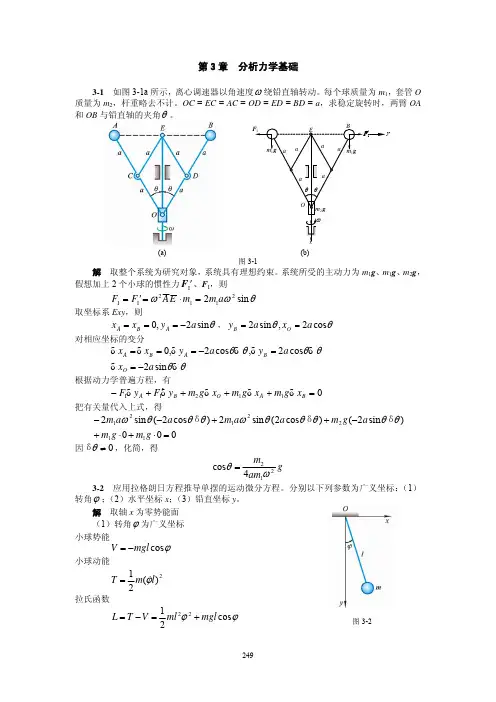
习 题3-1 台阶形鼓轮装在水平轴上，小头重量为2Q ，大头重量为1Q ，半径分别为2r 和1r ，分别挂一重物，物体A 重为2P ，物体重B 为1P ，且12P P >。

如3-1题图所示，求鼓轮的角加速度。

解：本题有明显的转轴o ，因而可以用角动量定理求解。

系统只有一个转轴，求运动而不求内力，所以取质心为研究对象。

因重力12,P P对轴o 的力矩不为零，可得：01122()L PQ PQ k =-质心系的动量距为：21202OQ OP OP k J J J J =+++2212121212211()22Q Q p p r r v v r k g g g gωωω=+++ 另外还有运动学补充方程：1122v r v r ωω==所以22220112211221(22)2J Q r Q r Pr P r k gω=+++应用角动量定理由 0i d J L dt =∑得 222211*********(22)2d Q r Q r Pr P r Pr g dtω+++=+11Pr 又 d dt ωε= 则有 11222222112211222()22Pr P r g Q r Q r Pr P r ε-=⋅+++答案：()12112222221122122d d 22Pr -P r g t Q r +Q r +Pr +P r ω=。

3-2 如图所示，两根等长等重的均匀细杆AC 和BC ，在C 点用光滑铰链连接，铅直放在光滑水平面上，设两杆由初速度为零开始运动。

试求C 点着地时的速度。

解： 系统在水平方向上受力为零，角动量守恒有2211222h mv m ω+⨯2（I ）=2g其中 002/2vv l l ω==0v 为C 点着地时A 点速度002c v v v ===答案：c v =3-3 半径为a ，质量为M 的薄圆片，绕垂直于圆片并通过圆心的竖直轴以匀角速度ω转动，求绕此轴的角动量。

3-2题图3-1题图解 由题意作图 如图所示由某一质点组对某个固定轴的动量矩1ni i i i J r m v==⨯∑20adm rd dr rdr d πρθρθ==⎰⎰其中2Ma ρπ=故 223001()2a J r dmv d r dr Ma πθρωω=⨯==⎰⎰⎰⎰答案：212J Ma ω=3-4 一半径为r ，重量为P 的水平台，以初角速度0ω绕一通过中心o 的铅直轴旋转；一重量为Q 的人A 沿半径B o 行走，在开始时，A 在平台中心。

理论力学第三章习题解答.ppt


量出FR的长度为161N 和水平方向的夹角为
FR FR2x FR2y 802 1402 161.2N
和水平方向（x轴）的夹角的余弦为
其余弦值为0.496
cos(FR,i ) Fx / FR 80 /161.2=0.496
2－3
解：
因为滑轮的大小忽略不计，且容易看出 AB和BC杆均为二力杆，容易得到B点的 受力如图所示：
Fx 0 FAx 0
FAy FB
Fy 0 FAy FB F 0
MA 0 FB 2a M F 3a 0
解得：
FAx 0
FAy
M Fa 2a
FB
M
3Fa 2a
3－6 （b）解：
AB杆的受力如图所示 显然，AB杆受一平面任意力
FAx
FAy
系作用，有平衡方程
Fx 0 FAx 0
FAx
FAy
系作用，有平衡方程
FB
Fx 0 FAx 0 Fy 0 FAy FB P1 P2 P 0
MA 0 FB (l1 l2) P1(l1 a) P2(l1 b) P(l1 l) 0
代入数值，解得：
FAx 0
FAy 33.23kN
FB 96.77kN
3－7
当成一整体，其受力如图所示
列平衡方程，有
FAx
FAy
Fx 0 FAx FT FBC cos 0
Fy 0 FAy FBC sin W 0
MB 0 FT r W(BD r) FAy (AD DB) 0
又因为 FT W
代入数值，解得
FAx 2400N FAy 1200N FBC 848.53N
A
x F1
FBD
B
60o
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

由上式可知hmin 的值与P的大小有关.
W b c b 2P 2 c 则 P W b
c P W b
综合分析， 可得如下的结果
10
c
当
W P W
c P W b

V ( ) PhD P(l cos a cot )
系统平衡时，势能满足：
y D
B
dV 1 Pl sin Pa 2 0 d sin
3

A a
C P
x
a sin 0 arcsin 3 a l l 注意：势能的零 2 2 cos 0 点应取在固定点 又： d V Pl cos 0 Pa 处,若取在A点,则 2 3 d sin 0
P
A
解：临界平衡时，B 处的反力为零。 各摩擦面处力的方向与法向所夹角
m m
等于摩擦角. ( 如图示)
W2
D
W1
B
f tg m
r R
FS
m
DB 2 Rr AB 2R
r R
FN
由题意 f
可满足条件.
12
P
A
m m
W2
D
W1
B
m
P
A
m
FR
K
W2
m
K
m
W1
R
O
m
即是
tg

Rr
C
arc tg
r

D
注: 系统的平衡时, W 与P的大小与角有关, 而角的大小取决于.
C
W
W
FS
P
FR
P
m
FN
8
例24. 均质矩形块置于粗糙的地板上, 摩擦系数为 , 初始静止. 为使矩形块 在水平力P的作用下沿地板滑动而不倾倒, 作用点不能太高, 即h 应比较小. 试问hmin = ? ( 第三届题)
B
C
系统或系统中的质点若被微小干扰 后只是在平衡位置附近运动而不会 产生很大的偏离, 且最终可恢复原 状,此种平衡状态是稳定平衡, 否则 便是不稳定平衡. 此题应是不稳定平衡. 判断平衡是 否稳定的标准式是 势能函数对其 坐标的二阶导数
P
A
O
O C
B
A
P
5
杆AB重P，长为2l ，下端靠在铅直的墙上， 同时又被支承在光滑的点C，求杆平衡时的角 度，并讨论平衡的稳定性。
2 h y A x B h2 2h
yA
yA 2vt v
vt 2 h2 h
v 2t
2 vt h 2
2
vt 2 h 2
2vt v 2
h
A
YA
vt 2 h2 t
B
XB
v
A v 2 y
x
vt 2 h2
解： 光滑面接触——理想约束
y D C x P
B

A a
系统中仅有重力作功——保守系统，可用 系统的势能决定其平衡位置及平衡的稳定 性。 系统的势能： 单自由度，取
为广义坐标
重力势能的零点取为点C
V ( ) PhD P(l cos a cot )
系统平衡时，势能满足：
dV 1 Pl sin Pa 2 0 d sin
FR
D
m
13
运动学篇
引言
运动学主要是确定或求解点和刚体运动时的位置、速度、角速度、加速 度、角加速度. 有两种基本方法: 点的运动形式: 直线、曲线 刚体的运动形式: 平动、定轴转动、平面运动、一般运动. 处理方法: 解析法 (函数法): (1) 通常只选定参考系, 直接描述点或刚体的绝对运动. 若有 必要描述相对运动, 则必须选择相应的动参考系. (2) 分析点或刚体在坐标空间中的任意时刻的几何位置,并将 其位置的坐标( 线坐标或角坐标)表示成时间的函数. (3) 求某瞬时的运动量, 应求得相应的运动解析式, 在将此时 刻的时间t或坐标值(角度或线度)代入之.
c b
hmin 0
b
C
Q
当
hmin
a
hmin
A
b W b c 0 2 2P
W
FS
B
P
FN
注:
c 在 hmin 0 及 W P W 条件下, b 物块在滑动中向左倒的趋向逐渐加大.
11
例25 小球重W2 半径为r, 大球重W1 半径为R. 设球与地面间、大球与小球间 的摩擦系数均为f , 现加一水平力P . 试问摩擦系数至少为多少,才能在足够大 的P力作用下保证大球从小球上翻过。（不计滚动摩阻）
3
FN
例21 . 轴AB与铅垂线成 角, 悬臂CD 固定于轴上并与之垂直. 悬臂CD长为a, 并与铅垂面ZAB成 角. 如图在D 点上作用一铅垂向下的力P, 求
m AB P ?
Z B

解: 将P 力正交分解, 其中, P1// AB, P2//EK . 显然, mAB P1 0 沿BA方向看下去如下图所示.

取长方块B 分析
Y
i
0:
FN W cos300 F2 si n350 0
FN 107 20 N .
F1
W
F2
F
B
30º
X
P
W
x
i
0:
F2 cos350 F W si n300 P 0 F FN tg350 75.06 N
P 4.34 N
vx C cos α v v
2
a x a τ cos α a n sinα 0 v a τ tgα a n tgα ρ
1 v 2 v3 a aτ2 a 2 n cosα ρ Cρ
19
例3. 设动点在一平面内运动. 求证:此点的运动轨迹的曲率半径有下式确定:
由此可得知: 只要
h
c 2
则不会倾倒.
因而有 hmax
c 2
至于hmin 可允许为零.
即hmin = 0 .
9
若P > W, 则在其作用下物块有一加速度a .
c
在图示的运动及受力状态下, 有hmin .
由图中可知,
W a P W g
P a g W
0
势能零点不定。
l P(l cos 0 2a cos 0 ) 3Pl cos 0 0 a 0为不稳定平衡！
例23. 半径为r, 重为W的均质圆柱体置于半径为R的圆槽底部, 接触面间的摩擦 系数为. 在圆柱体边缘缠绕一不计重量的柔索, 其端部悬挂重为P的物块, 则平 衡时圆柱体的中心可以升高, OC连线的最大偏角 可达 ( ) . ( 第三届题) 解: 当接触面处的静滑动摩擦力达到临界 值时, 角可达最大. 取圆柱体为研究对象, 由临界平衡可得
而
aA vA
vt
2
h
3 2 2

17
例2. 某一点的运动轨迹为平面曲线, 其速度在铅垂方向的投影始终是常量C. 求证: 任意时刻点的加速度大小 为:
v3 a C 其中, 为点所在曲线处的曲率 半径
证明: 不妨设铅垂轴为 轴 x 则 Vx C ax 0
18
又
v2 an ρ
Q W a P W g
b
C
Q
a
hmin
A
W
FS
B
P
b c mB 0 : Q W P hmin 0 2 2
hmin 1 Q b W c b W b c 2P 2 2P
FN
令上式中hmin = 0 若hmin > 0


1
Q
也可以将F1 , F2 正交分解为切向力和法向力, 基本 思路一样, 但计算过程要麻烦得多. 2
例19. 圆柱体A 与长方块B 均重100N , 置于倾角为30º的斜面上. 若所有接触处的摩擦角 都是35º. 求: 保持系统平衡所需的最小力P = ? 解: 设B 块向下滑动, 圆柱体A沿斜面滚动
例17. 小虫从半径为r 的半球形的碗底往上爬. 设虫与碗间的滑动摩擦系数为
f 3 3
求: 小虫爬到的最大的高度h = ?
解: 由滑动摩擦系数可知摩擦角为 O
30º 60º
h
tg
3 3
300
小虫爬到的最大高度h 时, 恰能自锁.
3 h r r sin60 r 1 2
14
合成法( 瞬时法):(1) 已知运动的点与未知的点在同一刚体上 刚体平面运动
基点法, VB VA VBA ( 包括速度投影及速度瞬心法)
n t a B a A a BA a BA
(2) 已知运动 的刚体(或点)和未知的刚体(或点)之间的相对运动— 点的合成运动.
Va Ve Vr
B
O
x
它有这样一重要的含义: 沿柔性体长度方向上的任 意两点的距离是保持不变的. – 这 正是刚体的性质. 这种性质的运动学表现是: 任意两点的速度沿长度 方向上的投影相等.
如图中
vC v B cos
vh
v A vC
v A v cos
vt 2 h 2
v 2 h2
aa ae ar aC
(3)刚体平面运动的基点法(合成法)之点的合成运动的动系是固
结在基点的平动坐标系. 而一般的点的合成运动的动系是固结在某运动刚体上的动系. 此动系可以是平动、定轴转动、刚体平面运动等任意形式的 刚体运动.