当前位置：文档之家 › 理论力学竞赛辅导全

理论力学竞赛辅导全

  • 格式：ppt
  • 大小：2.88 MB
  • 文档页数：130

下载文档原格式

  / 130

合集下载

理论力学竞赛辅导2运动学

理论力学竞赛辅导2运动学

问题3：当平面运动刚体的角速度或角加速度分别为零时， 如何确定加速度瞬心的位置？
2020/6/8
5
BUAA
例题与思考题
习题4：点M做平面曲线运动，已知该点速度的大小 v=at (a>0), 速度的方向与 x 轴的夹角θ=0.5bt2(b>0),求任意时刻(t>0) 动点M的加速度在y轴上的投影以及轨迹的曲率半径。
aOn
vO2 R
r
(r)2
3r
12r
3
aPnO 2r
aPn
aOn
aPnO
42r
3
vP2 aPn
( 2r ) 2 42r
3r
2020/6/8 3
an
P PO
r
O
an O R
14
BUAA
例题与思考题
问题14：圆盘上哪点的加速度的模最大（小）?
为
o
常
量
A
aA O
Ca
B D
aB
CV
纯滚动
OA R, AB 2R
vB vA vBA
2、速度投影法
vB
AB
vA
AB
3、速度瞬心法
vM vMCV , vM MCV
思考题1：上述三种方法的内 在联系和区别是什么？
Ax’y’为平移动系，B为动点
y
y' vBA vB B
A
r0
B
A
vA
x'
o
vA x
M
vM
CV
2020/6/8
4
BUAA
二、刚体的平面运动
4、平面图形上各点的加速度
y
et (t t)

全国周培源大学生力学竞赛辅导力学竞赛-静力学专题

全国周培源大学生力学竞赛辅导力学竞赛-静力学专题

B A
二力矩式
F F F x 0 , M A () 0 , M B () 0
FR x
（x 轴不得垂直于A、B 两点的连线）
是否存在三投影式？
三力矩式
F x1 0
M A ( F ) 0 , M B ( F ) 0 , M C ( F ) 0 Fra bibliotekFx2
0
（A、B、C 三点不得共线）
全国周培源大学生力学竞赛辅导力学竞赛-静力学专题
理论力学(专题部分)
专题1： 虚位移原理
掌握虚位移、虚功的概念；掌握质点系的自由度、 广义坐标的概念；会应用质点系虚位移原理。
专题2： 碰撞问题
(1) 掌握碰撞问题的特征及其简化条件。掌握恢复因 数概念
(2) 会求解两物体对心碰撞以及定轴转动刚体和平面 运动刚体的碰撞问题。
全国周培源大学生力学竞赛辅导力学竞赛-静力学专题
§2 平面任意力系的平衡条件和平衡方程
n
F xi 0
i1
｝ FR′ =0
Mo=0
n
F yi 0
i1
n
M O (F i) 0
i1
平衡方程
平面任意力系平衡的解析条件：所有各力在两个任选的坐标轴
上的投影的代数和分别等于零，以及各力对于任意一点矩的代
公理2 二力平衡条件
★ 作用在刚体上的两个力，使刚体保持平衡的充要条件是： 这两个力的大小相等，方向相反，且在同一直线上。
B A
F2
F1= F2
F1
注意： 公理对于刚体的平衡是充要条件，而对变形体仅为
平衡的必要条件；
全国周培源大学生力学竞赛辅导力学竞赛-静力学专题
公理3 加减平衡力系原理
★ 在已知力系上加上或减去任意的平衡力系，并不改变原力系

周培源大学生力学竞赛辅导材料

周培源大学生力学竞赛辅导材料

t 2H / g
e=1时，根据落下与反弹的轨迹对称性，设小球与地面碰撞N次，于是有
S=2NvBt，
S 2N 2gR(1 cos ) 2H / g
（3）假设小球击中CD杆上的E点，为了使悬挂点C处的冲量尽可能小，试确 定小球的号码及静止释放时的θ，此时CE的距离是多少？冲量有多大？ 根据碰撞的理论，当冲量IE与杆垂直，且
解：1. 圆环不是匀质的，质心不在圆环的中心。开始滚动角速度大，圆环一跳 一跳地向前滚动；随后角速度减小，所以圆环不离开地面向前滚动。
2.（1）圆环能自己滚回的条件：圆环初瞬时环心速度为v0，角速度大小为ω0，以后 为v 和ω。圆环与地面接触点的速度大小为 u=v+rω (1) 第一阶段，u>0，圆环与地面有相对滑动，摩擦力F=fsFN，式中FN=mg 。 由质心运动定理 解得 由 解得 由于摩擦力存在，v 和ω都随时间而减小。 第二阶段，由（1），（3），（5）式解得 u = (v 0 + r ω 0) −2 f s gt v=v0－fsgt
S 2 gR(1 cos )t 1 1 2 H H gt 2 2
把参数带入小球的位移表达式，有
S的限制为
S 2HR
（2）假设某小球击中CD杆上的E点，为了使E点尽可能远离D点，试确 定小球的号码及静止释放时的θ，此时CE的距离是多少？ 直观上看，当e=1（小球的号码为9）时反弹得最高，有可能击中C点。 此时E点离D点最远，距离为CE=0。 根据运动方程，在竖直方向，小球离开B点后与地面碰撞的时间为
不失一般性，设乘员的前脚向左蹬板，蹬板时前脚掌必自然倾斜使左侧略高于右 侧，并带动前板绕x轴逆时针偏转φ1角，前轮平面随同前板相对垂直平面偏转φ1角.此 时地面在P1点处作用的法向约束力N1必偏离前轮平面，其沿前轮平面法线方向的投影 为N1 sinφ1，仅保留φ1的一次项时，简化为N1φ1.此分量以a cosβ为力臂，产生绕前轮架 转轴z1;负方向的力矩M1，力矩的模为

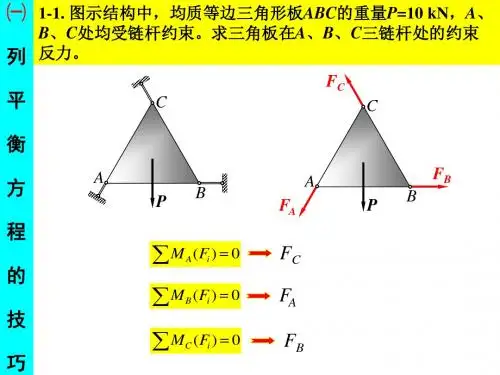
全国周培源大学生力学竞赛辅导力学竞赛-静力学平衡方程

全国周培源大学生力学竞赛辅导力学竞赛-静力学平衡方程

0.5 m C P
FAx FAy
FBy
解：研究系统，受力如图，由方程：∑Fx=0，∑Fy=0，∑MA=0，可 解得FAx=0、FAy=20 kN、MA=20 kN· m。
研究杆BEC，受力如图，由方程：∑Fx=0，∑Fy=0，∑MB=0，可 解得FBx=0、FBy=－20 kN、FDE=40 kN· m。
㈠ 1-1. 图示结构中，均质等边三角形板ABC的重量P=10 kN，A、
B、C处均受链杆约束。求三角板在A、B、C三链杆处的约束 列 反力。 FC 平 C C
衡 方 程 的 技 巧
A P
B
( Fi ) 0 ( Fi ) 0 (Fi ) 0
A FA P
FB B
M M M
A
FC FA
A A C B
D
FA
E
F P FC C FB
B
A FA D FD
C
B
E
F P
㈢ 3-1. 图示结构，已知P=20 kN，求支座A处反力及杆 物 DE的受力。 体 系 平 衡 问 题 基 本 解 法
B FBx 0.5 m A 0.5 m D B E C P D MA A B E C P
0.5 m
E FDE
0.6 m 0.6 m
A C
B
0.8 m
0.6 m
0.6 m
D
F
0.6 m 0.6 m
E
A M C
B
0.8 m
P 4-2′图示结构，已知 P=10 kN，求支座A、E处反力及 杆CF、BF的受力。 0.6 m 0.6 m
A M C
B
0.8 m
D P
F
0.6 m 0.6 m

力学竞赛辅导讲解

力学竞赛辅导讲解


an a
a
an
a
1.2 曲率半径的物理求法
an

v2




v2 an
y
椭圆的曲率半径：
B
轨道方程：
x2 a2

y2 b2
1
对应运动方程： xy

a b
cos t sin t
b Oa
Ax
A点：v vy,max b,
A

v2 an

b2 a
an ax,max a2

v02 h
sin3
h v0
y
x

例1.8 如图示，一半径为R的半圆柱体沿水平方向
以速度v0作匀速运动。求杆与半圆柱体的接触点P
的角位置为 时竖直杆运动的速度和加速度。
vP
P
R
y
v0
O xA
解：y R2 x2
dy dy dx
dy
vP dt dx dt v0 dx v0
反映速度（大小和方向） 变化快慢的物理量
a v
a

t lim
t 0
v t

dv dt

d 2r dt 2
x
a x

dvx dt

d2x dt2
a y

dvy dt
d2y dt 2
z A
vA B
rA
vB
rB
O
y
(a)
vA v
vB (b)
加速度与速度的方向一般不同。
H

ymax

v02 sin2
2g

力学竞赛辅导讲义

力学竞赛辅导讲义

力学竞赛辅导讲义——虚位移原理一、内容要点精讲1、约束与约束方程（1）约束。

限制非自由质点或质点系运动的各种条件称为约束。

（2）约束方程。

约束对质点系运动的限制可以通过质点系中各质点的坐标和速度以及时间的数学关系式或方程来表示。

这种方程通常称为约束方程。

2、约束分类（1）几何约束与运动约束。

只限制质点或质点系几何位置的约束称为几何约束；对于不仅限制质点系的位置，而且还限制质点系中质点的速度的这类约束称为运动约束。

（2）定常约束（稳定约束）与非定常约束（不稳定约束）。

约束方程中不显含时间t 的约束称为定常约束（或稳定约束）；约束方程中显含时间t 的约束称为非定常约束（或不稳定约束）。

（3）完整约束与非完整约束：约束方程中不包含坐标对时间的导数，或者方程中的微分项可以积分为有限形式，这类约束称为完整约束；约束方程中包含坐标对时间的导数，而且方程中的微分项不能积分为有限形式，这类约束称为非完整约束。

（4）单侧约束（可离约束）与双侧约束（不可离约束）。

由不等式表示的约束称为单侧约束（或可离约束）；由等式表示的约束称为双侧约束（或不可离约束）3、虚位移在某瞬时，质点系在约束允许的条件下，可能实现的无限小位移称为虚位移。

虚位移可以是线位移，也可以是角位移。

在定常约束条件下，微小实位移是虚位移之一。

4、虚位移与实位移的差别和联系(1) 差别。

虚位移是纯粹的几何概念，它与质点或质点系是否实际发生运动无关。

它不涉及运动时间、运动的初始条件和作用力等，只是约束许可的想像中的微小位移。

而实位移除与约束有关外，还与运动时间、运动初始条件和作用力、质量等有关；虚位移是微小的位移，而实位移可能是微小的，也可能是有限的；虚位移可以有多种不同的方向，而实位移只有惟一确定的方向，指向真实运动的一边。

(2) 联系。

在定常约束条件下，微小的实位移是虚位移中的一种情形。

在非定常约束条件下，微小的实位移一般不是虚位移中的一种情形。

为区别起见，虚位移用变分符表示，如r (投影为x，y，z)，s 等，而微小的实位移用微分符号d表示，如dr (投影为dx，dy，dz)，ds，d等。

理论力学竞赛辅导5综合应用PPT精品文档19页

理论力学竞赛辅导5综合应用PPT精品文档19页

01.06.2020
11
BUAA
动力学的应用
1、电机的驱动力矩M 应用动能定理微分形式：
T1 2m Cv21 2m Av21 2JAR v2 dWM d
T m Cv am Av aJAR v2aW MMRv
M(mCRmARR J)a
C θ
mCg
a A
F
2、求倾角θ 应用动静法：研究车身
M A0, FICmCa
01.06.2020
1、 若钢板能进入碾轧机，利 用的是什么力学概念？ 2、轧轮和钢板间的摩擦系数 为f，确定a,b,d ,f间的关系。
ftam na x tan
5
BUAA
运动学的应用
问题5：已知车队以速度V 匀速行驶，车宽为b，车距为a, 若人要
匀速沿直线行走穿过马路，求人过马路的最小速度u，并确定过
马路的方向。
au
b
V
V ta(uco )ts f() a s i n b c os
(usin )tb
f'() a co b s si 0 n
uasinVbbcos
tan a
b
u Vb a2 b2
01.06.2020
6
BUAA
运动学的应用
问题6：设计一个机构，使得将转动转换成往复移动或摇动。
01.06.2020 问题3：该磅秤在设计上存在还哪些不足，如何改进2 。
BUAA
静力学的应用
问题3：该磅秤在设计上存在还哪些不足，如何改进。
01.06.2020
3
BUAA
静力学的应用
01.06.2020
4
BUAA
静力学的应用
问题4：轧钢机械中的力学问题

理论力学竞赛辅导动力学

理论力学竞赛辅导动力学

试题范围（专题部分）
(一) 虚位移原理 掌握虚位移、虚功旳概念；掌握质点系旳自由度、广义坐 标旳概念；会应用质点系虚位移原理。 (二) 碰撞问题 (1) 掌握碰撞问题旳特征及其简化条件。掌握恢复因数概念 (2) 会求解两物体对心碰撞以及定轴转动刚体和平面运动刚 体旳碰撞问题。
基本概念—质心速度
Fgox (miaix) 如图11-2所示旳四杆机构中，各均质杆质量均为，
F2
v2 v1 N PF1 F2
N P F1 F2 v2 v1
定常流动时，管内流体在单位时间内流出动量与流入动量之差等于作用 于管内流体上旳全部外力之矢量和。流体流动欧拉定理
pv v t Wp (p1 p2)V
静约束力 附加动约束力
21
定常流动中旳能量方程（动能定理在流体中旳应用）
Fgoz 0 J yz
FAx
1 AB
My
FRxOB
Mgoy
FgoxOB
mi yi z i
M goy miaix zi mi ( 2 xi yi )zi J xz 2 J yz
M goz mi ai t riz mi riz2 J z
2 mi xi mi yi m(xC 2 yC )
根据本题旳启示，设计一种力学小魔术：不依托任何外力矩， 倒立摆可在任何倾角处保持不动甚至能从倾斜状态竖立起来。
魔术师旳表演（25分）第六届预赛样题
魔术师要表演一种节目。其中一种道具是边长为a旳不透明立方体箱子，质量为M； 另一种道具是长为L旳均质刚性板AB，质量为2M，可绕光滑旳A铰转动；最终一种 道具是半径为R旳刚性球，质量为3M，放在刚性旳水平面上。魔术师首先把刚性板 AB水平放置在圆球上，板和圆球都能够保持平衡，且圆心O和接触点B旳连线与垂 线夹角为ϕ。然后魔术师又把箱子固定在AB板旳中间位置，系统仍能够保持平衡， 如图3所示。 魔术师用魔棒轻轻向右推了一下圆球，居然轻易地就把圆球推开了。 更令人惊讶旳是，当圆球离开AB板后，AB板及其箱子仍能在水平位置保持平衡。

竞赛辅导(第一、四章)0

竞赛辅导(第一、四章)0

第一、四章力和物体的平衡专题一受力分析法正确分析物体的受力情况，作出五的受力示意图，是研究力学问题的关键，是必须掌握的基本功。

物体受力分析，主要是依据力的概念，从物体所处的环境和运动状态着手，分析它与其他物体的相互作用。

【要点突破】一．对物体进行受力分析（隔离法）的基本步骤首先确定研究对象，一般要单独画出所选定的受力物体。

其次是把研究对象与周围的物体隔离开来，找出周围物体对其产生的力的作用。

一般按照重力、弹力或已知力、摩擦力等的顺序进行分析，并正确合理地画出各力的示意图，标上各力的符号。

最后是检查是否分析多力或漏力。

二．在判断某一性质的力是否存在及其大小和方向问题的常用方法1．由该种性质的力的产生条件来分析弹力的产生条件是直接接触及产生形变；摩擦力的产生条件是直接接触并相互挤压，且有相对运动或相对运动趋势。

但物体的微小形变和相对运动趋势较难判断，所以可用一些特殊的方法来判断。

2．假设法判断是否有支持力或压力产生时，可假设去掉支持物，或假设就有支持力和压力的存在，分析物体是否能保持原有状态；判断是否有摩擦力时，可假设接触面光滑，或假设就有摩擦力，分析物体是否能保持原有状态。

3．把物体的运动状态和所受其他力的情况相结合来判断力是物体改变运动状态的原因，物体的运动状态与它的受力情况是相对应的，所以可以由物体的运动状态来判断它的受力情况。

三、在确定研究对象并对其进行受力分析时常要把整体法与隔离法相结合。

整体法是指以若干个相互作用的物体组成的一个整体——系统为研究对象，分析系统外的物体对系统内物体的作用力——外力，而不用考虑系统内物体间的作用力——内力。

通常在分析系统外来时用整体法；在分析系统内各物体或各部分间的相互作用时用隔离法。

【典例剖析】【例1】分别画出图中A、B两物体的受力示意图(1到5中A 和B 均静止).A CACBAθ⑴⑵⑶ABθ⑷斜面光滑BA⑸容器与球光滑BA F⑹接触面均不光滑,A和B分别向左、向右运动悬线C斜向左悬线C竖直【例2】如图所示，两只相同的均匀光滑小球置于半径为R的圆柱形容器中，且小球的半径r满足2r>R，则以下关于A、B、C、D四点产生的弹力大小的说法中正确的是 ( )A．D点的弹力可以大于、等于或小于小球的重力B．D点的弹力大小等于A点的弹力大小C．B点的弹力恒等于一个小球重力的2倍D．C点的弹力可以大于、等于或小于小球的重力【例3】如图，把一质量为m的小物块轻轻地放上以恒定速度匀速运转的水平传送带上，假设传送带AB间足够长，物块与带间的动摩擦因数为μ。

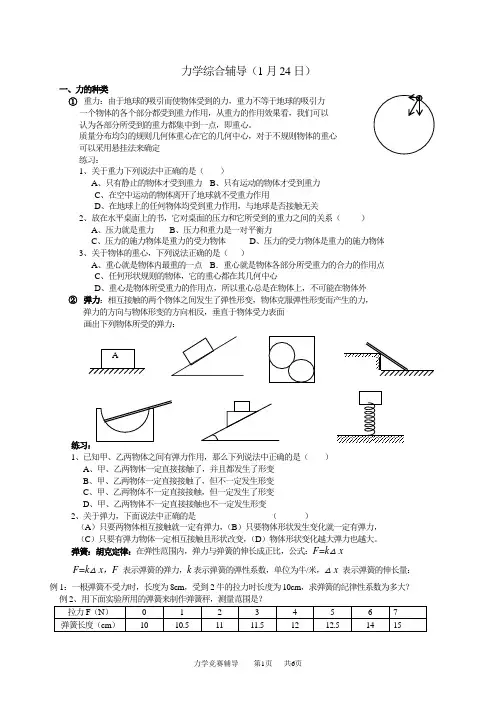
初中物理竞赛辅导 力学综合辅导1(1月24日)

初中物理竞赛辅导 力学综合辅导1(1月24日)

力学综合辅导（1月24日）一、力的种类① 重力：由于地球的吸引而使物体受到的力，重力不等于地球的吸引力一个物体的各个部分都受到重力作用，从重力的作用效果看，我们可以认为各部分所受到的重力都集中到一点，即重心。

质量分布均匀的规则几何体重心在它的几何中心，对于不规则物体的重心可以采用悬挂法来确定练习：1、关于重力下列说法中正确的是（ ）A 、只有静止的物体才受到重力B 、只有运动的物体才受到重力C 、在空中运动的物体离开了地球就不受重力作用D 、在地球上的任何物体均受到重力作用，与地球是否接触无关2、放在水平桌面上的书，它对桌面的压力和它所受到的重力之间的关系（ ）A 、压力就是重力B 、压力和重力是一对平衡力C 、压力的施力物体是重力的受力物体D 、压力的受力物体是重力的施力物体3、关于物体的重心，下列说法正确的是（ ）A 、重心就是物体内最重的一点B ．重心就是物体各部分所受重力的合力的作用点C 、任何形状规则的物体，它的重心都在其几何中心D 、重心是物体所受重力的作用点，所以重心总是在物体上，不可能在物体外② 弹力：相互接触的两个物体之间发生了弹性形变，物体克服弹性形变而产生的力，弹力的方向与物体形变的方向相反，垂直于物体受力表面画出下列物体所受的弹力：1、已知甲、乙两物体之间有弹力作用，那么下列说法中正确的是（ ）A 、甲、乙两物体一定直接接触了，并且都发生了形变B 、甲、乙两物体一定直接接触了，但不一定发生形变C 、甲、乙两物体不一定直接接触，但一定发生了形变D 、甲、乙两物体不一定直接接触也不一定发生形变2、关于弹力，下面说法中正确的是 （ ）（A ）只要两物体相互接触就一定有弹力，（B ）只要物体形状发生变化就一定有弹力，（C ）只要有弹力物体一定相互接触且形状改变，（D ）物体形状变化越大弹力也越大。

弹簧：胡克定律：在弹性范围内，弹力与弹簧的伸长成正比，公式：F=k △xF=k △x ，F 表示弹簧的弹力，k 表示弹簧的弹性系数，单位为牛/米，△x 表示弹簧的伸长量：例1：一根弹簧不受力时，长度为8cm ，受到2牛的拉力时长度为10cm ，求弹簧的纪律性系数为多大？ A例3、有k1、k2两根弹簧，若将它们并列起来使用，下挂一个重为G的重物，弹簧的伸长为多大？串联起来使用呢？若将一根弹簧剪断为相等的两部分后，每一部分弹簧的弹性系数为多大？例4、如图所示，k1、k2为两根轻质弹簧，k1>k2，a、b是质量分别m1、m2的两个物体，且m1>m2按如图所示方式悬挂起来，要使弹簧的总长度最短，则应该如何悬挂？练习：1、两根轻质弹簧的原长都是10cm，弹性系数都是k=10N/m，小球重力都是1 N，小球大小不计，球两根弹簧的总长度为(50cm)2、如图示，一弹性系数为k2的弹簧竖直放在水平桌面上，其上压一质量为m的物体，另一弹性系数为k1的弹簧竖直地放在物体上面，其下端与物体上表面相连，两个弹簧的质量均不计，要想使物体在静止时，下面弹簧的支持力为原来的2/3，应将上方弹簧的上端竖直向上提高一段距离d，则d=（k1+k2）mg/(3k1k2)练习2图图3、一根轻质弹簧原长这l，将其上端固定，在离上端2/3处剪断弹簧，把重为G的物体挂在其下端，再将剪下的弹簧挂在重物G下端，再在下面弹簧下面挂重力为P的重物，平衡时，上下两部分弹簧伸长量相同，则P=_________G4、一根弹簧秤，不挂重物时，读数为2 N，挂100 N重物时，读数为92 N，当读数为20 N时，所挂重物的实际重为（）（A）16 N，（B）18 N，（C）20 N，（D）22 N。

高中物理竞赛辅导力学部分专用讲义

高中物理竞赛辅导力学部分专用讲义

高中物理《竞赛辅导》力学部分目录第一讲：力学中的三种力第二讲：共点力作用下物体的平衡第三讲：力矩、定轴转动物体的平衡条件、重心第四讲：一般物体的平衡、稳度第五讲：运动的基本概念、运动的合成与分解第六讲：相对运动与相关速度第七讲：匀变速直线运动第八讲：抛物的运动第九讲：牛顿运动定律（动力学）第十讲：力和直线运动第十一讲：质点的圆周运动、刚体的定轴转动第十二讲：力和曲线运动第十三讲：功和功率第十四讲：动能定理第十五讲：机械能、功能关系第十六讲：动量和冲量第十七讲：动量守恒《动量守恒》练习题第十八讲：碰撞《碰撞》专题练习题第十九讲：动量和能量《动量与能量》专题练习题第二十讲：机械振动《机械振动》专题练习第二十一：讲机械波第二十二讲：驻波和多普勒效应第一讲： 力学中的三种力【知识要点】（一）重力重力大小G=mg ，方向竖直向下。

一般来说，重力是万有引力的一个分力，静止在地球表面的物体，其万有引力的另一个分力充当物体随地球自转的向心力，但向心力极小。

（二）弹力1．弹力产生在直接接触又发生非永久性形变的物体之间(或发生非永久性形变的物体一部分和另一部分之间)，两物体间的弹力的方向和接触面的法线方向平行，作用点在两物体的接触面上．2．弹力的方向确定要根据实际情况而定．3．弹力的大小一般情况下不能计算，只能根据平衡法或动力学方法求得．但弹簧弹力的大小可用．f=kx(k 为弹簧劲度系数，x 为弹簧的拉伸或压缩量)来计算 ．在高考中，弹簧弹力的计算往往是一根弹簧，而竞赛中经常扩展到弹簧组．例如：当劲度系数分别为k 1,k 2,…的若干个弹簧串联使用时．等效弹簧的劲度系数的倒数为：nk k k 1...111+=，即弹簧变软；反之．若以上弹簧并联使用时，弹簧的劲度系数为：k=k 1+…k n ，即弹簧变硬．(k=k 1+…k n 适用于所有并联弹簧的原长相等；弹簧原长不相等时，应具体考虑) 长为0L 的弹簧的劲度系数为k ，则剪去一半后，剩余2L 的弹簧的劲度系数为2k （三）摩擦力 1．摩擦力一个物体在另一物体表面有相对运动或相对运动趋势时，产生的阻碍物体相对运动或相对运动趋势的力叫摩擦力。

力学竞赛辅导_图文

力学竞赛辅导_图文

(a)
vA v
vB (b)
2. 抛体运动
速度：
y
v0
运动方程：
g

O
x
轨道方程：
推论
y
v0
g

O
x
乙

s
甲 h
3. 圆周运动
3.1 圆周运动的加速度
0
v
a P
a
an
s
O R P0 x n0
3.2 圆周运动的角量描述
角位置：=(t)
角速度: 角加速度:
3.3 角量和线量的关系
P
s
椭圆的曲率半径： 轨道方程： 对应运动方程： A点：
y B
b Oa
Ax
同理：
抛物线的曲率半径： 轨道方程： 对应运动方程：
其中：
y
O
x
2. 连体运动问题
解题方法一：运动的分解
情形1：两物体通过刚性细杆或不可伸长的绳子相连， 他们在连线方向的位移、速度和加速度相等。

v1
v2

情形2：两刚性物体接触点的速度沿法向分量相等。
3.刚体平衡的稳定性
满足平衡条件的刚体，若受到扰动，便离开 平衡位置。若它会自动回到平衡位置，则称为稳 定平衡；若它会更远离平衡位置，则称为不稳定 平衡；若平衡位置的周围仍是平衡位置，则称为 随遇平衡。
稳定平衡
不稳定平衡
随遇平衡
4. 质心
y
C
O
x
5．质心运动定理
系统质心加速度的大小与于所受的合外力大小 成正比，与系统的总质量成反比，加速度的方向沿 合外力的方向。
之间的摩擦系数=0.5。今用一恒力F 沿水平方向作

理论力学竞赛指导

理论力学竞赛指导

计算题解题技巧
01
认真审题，明确题目所考查的知识点和解题要求，建立正确的 物理模型。
02
根据物理模型列出相应的方程或表达式，注意方程或表达式的
准确性和完整性。
对于复杂的计算题，可以采用分步计算的方法，逐步求解，确
03
保计算过程的清晰和准确性。
证明题解题技巧
01
仔细阅读题目，理解题目所要求证明的结论和已知条
动量定理与动量守恒定律
描述物体系统动量变化与外力之间的关系，以及在 特定条件下系统内动量守恒的规律。
动能定理与机械能守恒定 律
描述物体动能变化与外力做功之间的关系， 以及在特定条件下系统内机械能守恒的规律 。
03
竞赛题型与解题技巧
选择题解题技巧
01
仔细阅读题干，理解题目要求，注意题目中的关键词和限制 条件。
性和有效性。
设计试卷结构
合理规划试卷的题型、题量、分值等， 确保试卷结构的科学性和合理性。
组建命题小组
邀请具有丰富教学经验和命题经验的 教师组成命题小组，共同商讨试卷的 设计和制作。
编制试题
按照设计好的试卷结构，编制高质量 的试题，注意试题的难易程度、区分 度和覆盖面。
模拟考试组织实施
安排考试时间
件。
02
根据已知条件选择合适的物理定理或定律进行证明，
注意定理或定律的适用条件和范围。
03
在证明过程中要注意逻辑严密性和推理的合理性，确
保证明过程的正确性和完整性。
04
历年竞赛真题解析
历年竞赛真题回顾
01
回顾近五年的理论力学竞赛真 题，包括选择题、填空题和计 算题。
02
分析历年真题的考点分布和命 题规律，总结常考知识点和题 型。

力学竞赛辅导讲义

力学竞赛辅导讲义

力学竞赛辅导讲义——碰撞一、内容要点精讲1、碰撞的定义两个或两个以上相对运动的物体在瞬间接触，速度发生突然改变的力学现象称为碰撞。

2、碰撞现象的基本特征碰撞过程时间极短．碰撞物体在这一过程中的位移可略去不计，但速度可产生有限变化。

碰撞时产生的碰撞力可能极大并发生急剧变化，难以测量。

通常用碰撞力在碰撞过程中的冲量来度量碰撞的强弱，碰撞冲量为式中，v和u分别是物体作为质点在碰撞开始瞬时和碰撞结束瞬时的速度。

3、研究碰撞问题的两点基本假设(1)在碰撞过程中，普通力（非碰撞力）的冲量忽略不计；(2)在碰撞过程中，物体的位移忽略不计。

4、碰撞过程的两个阶段(1)变形阶段。

从两个物体开始接触到两者接触点处沿公法线方向无相对速度为止，这时变形获得最大值。

(2)恢复阶段。

从两个物体接触点处在公法线方向获得分离速度到两个物体脱离接触为止。

在这阶段中物体的变形得到部分或全部恢复。

5、碰撞的分类碰撞时两物体间的相互作用力，称为碰撞力。

（1）按物体的相处位置分类对心碰撞与偏心碰撞：若碰撞力的作用线通过两物体的质心，称为对心碰撞，否则称为偏心碰撞。

见下图(a),图(b)正碰撞、斜碰撞：若两物体碰撞时各自质心的速度均沿着接触处的公法线，称为正碰撞；否则称为斜碰撞。

下图中，AA 表示两物体在接触处的公切面，BB 为其在接触处的公法线(2) 按其接触处有无摩擦，分为光滑碰撞与非光滑碰撞。

(3) 按物体碰撞后变形的恢复程度(或能量有无损失)，可分为完全弹性碰撞、弹性碰撞与塑性碰撞。

（1k =，完全弹性碰撞；0k =，非弹性碰撞或塑性碰撞；01k ,弹性碰撞）6、恢复因数K恢复因数K 表示物体在碰撞后速度的恢复程度，也表示物体变形恢复的程度，并反映出碰撞过程中机械能损失的程度。

（1）正碰撞k式中和分别表示碰撞开始和碰撞结束时质心的速度。

（2）斜碰撞k和分别是入射角和反射角式中αβ（3）两物体相互碰撞式中分别为两物体的碰撞点在碰撞结束和碰撞开始时沿接触面法线方向的相对速度。

理论力学竞赛培训—运动学1

理论力学竞赛培训—运动学1

详细的说明见《理论力学》哈工大第六版P179～180。
dvr dt
= ar
+ ωe × vr
dve dt
=
ae
+ ωe × vr
由：
dva dt
=
dve dt
e
+ ar
+ 2ω × vr
所以： a=c 2ω × vr 其大小为： ac = 2ωvr sinθ
运动方程= ： xO' f1= (t ), yO' f= 2 (t ), ϕ f3 (t )
2. 平面运动的分解 对于任意的平面运动，可在平面图形上任取一点O’，称为基点。 在这一点假想地安上一个平动的参考系O’x’y’z’ ；平面图形运 动时，动坐标轴方向始终保持不变（可令其分别平行于定坐标 轴Ox和Oy）。于是，平面图形的平面运动可看成随同基点的平 动和绕基点转动这两部分运动的合成。
结论：平面运动可取任意基点而分解为平动和转动，其中平动 的速度和加速度与基点的选择有关，而平面图形绕基点转动的 角速度和角加速度与基点的选择无关。
3. 平面图形上各点的速度
⑴ 基点法：平面图形内任一点的速度等于基点的速度与该点随
图形绕基点转动速度的矢量和。 v=M vO' + vMO'
⑵ 速度投影定理：同一平面图形上任意两点的速度在这两点连
绝对轨迹、绝对速度、绝对加速度：指动点在绝对运动中的轨迹、 速度和另速度。
牵连速度、牵连加速度：在动参考系上与动点重合的那一点（牵
连点）的速度和加速度。
2. 速度合成定理
va= ve + vr
动点在某瞬时的绝对速度等于它在该瞬时的牵连速度与相对速
度的矢量和。

2023年力学竞赛辅导三动力学普遍定理

2023年力学竞赛辅导三动力学普遍定理

力学竞赛辅导三 动力学普遍定理一、基本力学量的计算: 1.质点系及刚体动量的计算质点系质心的位置矢量及坐标:例1: 求图示系统的总动量。

(1)传动皮带的质量为m, 积极轮的角速度为 , 积极轮与从动轮的质量分别为, 半径分别为 , 设传动皮带和传动轮的质量都是均匀的。

(0)(2)长均为l, 质量均为m 的均质杆OA, OB 在O 处以光滑铰链连接。

（2mv, mv ）(3)质量为m1, 半径为R 的均质圆盘与质量为m2, 长度为l 的均质杆铰接于A 点。

图示瞬时圆盘速度为v, 杆的角速度为 。

解： 圆盘与杆均为平面运动, 以A 为基点, 则杆：2. 转动惯量:定义: 质量连续分布:计算: （1）运用回转半径: 其中m 为整个刚体的质量, 由 得 为刚体对z 轴的回转半径, 具有长度的量纲。

（2）积分法（3）平行轴定理:（4）组合法求转动惯量:C i i m m v v p ==∑mz m z m y m y mx m x m m m m ii C i i C ii C ii i i i C ∑=∑=∑=∑=∑∑=,,r r r AB O (cos )sin ,2C A CA A CA CA A CA l v v v v v v ωθθ=+=+==v v v i +j,121221222[(cos )]sin 22[()cos ]sin 22AC C l l m m m v m v m l l m m v m m ωωθθωωθθ=+=+++⇒=+++p v v i jp i j若机构由几个简朴形状的刚体组成, 则分别求每个刚体对轴的转动惯量, 然后再叠加。

（5）实验法常用: 均质圆盘对盘心轴的转动惯量: 圆环:均质细直杆对一端的转动惯量:213ml 均质细直杆对中心轴的转动惯量: 2112ml3.质点系动量矩的计算下面证 即质点系对质心C 的动量矩:由质心坐标公式: ——即质点系对任意定点O 的动量矩, 等于集中于质心的系统动量对点O 的动量矩与质点系对质心C 的动量矩的矢量和。

大学物理竞赛辅导

大学物理竞赛辅导

麦杆以均匀的角速度旋转，甲虫沿麦杆爬行的速度 麦杆以均匀的角速度旋转， 多大？ 多大？ v 解： 以麦杆和甲虫为系统
0
o
12v0 解得： 解得：ω = 7l
碰撞过程角动量守恒，设碰后系统的角速度为ω 碰撞过程角动量守恒，
2 1 l 1 2 于是有： 于是有： mv0 = ml + m l ω 4 4 12
dω l J = mg cos θ dt 2 1 这里 J = ml 2 3 dω 3 g cos θ = 得到角加速度 2l dt 表达式可写成 dω = dω dθ = 3g cos θ 2l dt dθ dt dω 3g ω = cos θ 2l dθ 3g ωdω = cos θdθ 2l
θ
2 2
r
细杆质心C将沿着圆的渐开 细杆质心 将沿着圆的渐开 线运动 2 l 4ω0 R dvC dvC dr dθ = = 切向加速度为 aC切 = 2 2 2 (l + 3r ) dt dr dθ dt
法向加速度为
aC法
2 l 2ω0 r = rω = 2 l + 3r 2
N
2
A
l
v C r
θ
P
µ
,问 问
µ
为何值时
T2
T1
2m
m
T2
T1
2mg
mg
列方程: 列方程
对于盘2： 对于盘 ：
t
ω10
o1
N1
f
r1
N2
r2
dω 2 J2 = fr2 dt
dω 2 fr 2 = dt J2
o2
f
fr2 dω 2 = dt J2
m1 g

理力竞赛辅导1

理力竞赛辅导1

MO
0
MOx(F ) 0
MOy(F ) 0
M x(F) 0 M y (F ) 0,
Fz 0
MOz(F ) 0
M z(F) 0
注：坐标轴正交是力系平衡的充分条件，不是必要条件。
2020/11/10
9
BUAA
空间汇交力系的平衡条件
空间汇交力系平衡条件的讨论
FR FRxi FRy j FRzk 0
2020/11/10
17
BUAA
虚位移与理想约束
思考题11: 杆匀角速度转动,确定图示瞬时质点的虚位移
r y 对于定常约束,实位移是虚位移之一
n
x
FNi • ri 0
i 1
• 理想约束: 质点系中所有约束力在任何虚位移上所作
虚功之和为零的约束。
思考题12：若两物体之间 有摩擦，系统是否一定不 是理想约束。
12
BUAA
四、虚位移原理
•元功: W F • vdt F • dr, W M • ωdt M • dθ
等效力系作功定理: 若作用于刚体上的力系等效
即: {F1, F2,, Fn} {P1,, Pm} {FR , Mo}
n
m
则 W (Fi ) W (Pj ) W (FR ) W (MO )
•自由度: 广义坐标的数目k（在完整约束情况下）
2020/11/10
k = 位形坐标数 - 独立的约束方程数
15
BUAA
约束的分类
问题10: 图示系统具有什么 类型的约束？试确定系统的 自由度和广义坐标。
o
yA sin t
A
x
l
RA
B r
y
图
B
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

II
B
A I
选择题28: 长方体I面上的A点作用 一该平面内的汇交力系，II面上的B 点也作用有一该面内的汇交力系，则 该力系最多有几个独立的平衡方程？ A:2个 B:3个 C:4个 D:5个
B A
地面光滑
18
BUAA
虚位移原理
虚位移原理：具有双面、完整、 定常、理想约束的静止的 质点系， 在给定位置保持平衡的充要条件是：该质点系所 有主动力在系统的任何虚位移上所作的虚功之和等于零。
思考题13：判断在图示位置系统是否 有可能平衡．（F，M 均不为零）
C
CF
AM
B
A F
2020/10/18
0
MOx(F ) 0
MOy(F ) 0
M x(F) 0 M y (F ) 0,
Fz 0
MOz(F ) 0
M z(F) 0
注：正交条件是充分的，不是必要的。
2020/10/18
9
BUAA
空间汇交力系的平衡条件
空间汇交力系平衡条件的讨论
FR FRxi FRy j FRzk 0
A
O RC
mg
1. 不倒翁的质量m 2. 半圆球的半径R 3. 重力加速度g 4. 重心的位置h
2020/10/18
21
BUAA
静力学的思考题与例题
题15：在下列图示结构中，构件AC上作用有一已知力偶（构 件自重不计），试确定铰链A处约束力的方向。
AB AC, AC AB
思考题16：上述结构中，哪个结构中A点的约束力最大？
FR FR2x FR2y FR2z 0
FRx Fx FRy Fy FRz Fz
空 FRx Fx 0
间
力
FRy
Fy 0
系
FRz
Fz
0
有三个独立的平衡方程
z
?
x y
问题6：三根轴必须垂直吗？
2020/10/18
10
BUAA
三、刚体系与结构的平衡
•静 定 问 题 ( statically determinate problem): 未知量的数目= 独立平衡方程的数目
12
BUAA
四、虚位移原理
•元功: W F •vdt F •dr
等效力系作功定理: 若作用于刚体上的力系等效
即: {F1, F2,, Fn} {P1,, Pm} {FR , Mo}
n
m
则 W (Fi ) W (Pj ) W (FR ) W (MO )
i1
j 1
问题9: 如何求纯滚动圆盘轮心移动S距离时, 力F 所作的功。
7
BUAA 一、基本概念与基本原理和定理
选择题２: 力偶系和一个力构成的力系简化的最简结果可能是: A:平衡力系、B:力偶、C:合力、D:力螺旋
选择题３: 两个平面汇交力系构成的平面力系简化的最简 结果可能是: A:平衡力系、B:力偶、C:合力、D:力螺旋
选择题４: 图中的两个力构成的力
系简化的最简结果可能是: A:平衡力系、B:力偶、
M1 B
I
M B
I
II M2 A
F A
问题22：该 系统是否是 静定结构？
思考题21：重为W的均质正方体用球铰链约束，其上作用有一 个力和一个力偶（如图所示），求平衡时力与力偶的关系。设 正方体的棱长为L。
2020/10/18
25
BUAA
静力学的思考题与例题
问题23：空间汇交力系的平衡方程独立的充分必要条件：
F1
II I
C:合力、 D:力螺旋
F2
选择题5: 若作用在立方体上的力系由作用在I面和II面上的两
个平面任意力系构成，该力系简化的最简结果可能是:
A:平衡力系、B:力偶、C:合力、D:力螺旋
2020/10/18
8
BUAA 二、空间任意力系的平衡条件
空间任意力系简化 {F1, F2,, Fn} {FR, MO}
M l1 0 M l2 0
l2
M l3 0
l4
M l4 0 M l5 0
M l6 0
Mo 0
？ FR 0
2020/10/18
27
BUAA
静力学的思考题与例题
选择题27: 长方体I面上的A点作用一 该平面内的汇交力系，II面上的B点也 作用有一该面内的汇交力系，则该力 系最多有几个独立的平衡方程？ A:2个 B:3个 C:4个 D:5个
BUAA
问题10: 图示系统具有什 么类型的约束？试确定系 统的自由度和广义坐标。
RA
B r
图 1 齿轮机构
2020/10/18
约束的分类
o
yA sin t
A
x
l
y 图2B
A
B O
图 3 圆盘放置在光滑地面上 16
BUAA
虚位移与理想约束
•虚位移: 在给定瞬时，质点或质点系为 约束容许 的 任何 微
n
Fi • ri 0
i 1
M B
F
F
19
BUAA
平衡位置的稳定性
设质点系的势能函数为：V V (q1, q2,, qk )
质点系在势力场中的平衡充分必要条件是：
V 0,( j 1,, k) q j
质点系势能函数取得 极值是平衡的充分条件
定理：质点系在势力场中的平衡位置是稳定的充分必要 条件是系统在平衡位置的势能为极小值。
确定三根轴的位置
26
BUAA
静力学的思考题与例题
思考题26：长正方体上作用有一空间任意力系，对 其中的六个轴取矩方程均成立，该力系是否是平衡 力系。
MO
l3 FR
l5
MO
l3 FR
o
l6 l2
l6 o
l1
l4
l1
{F1, F2 ,, Fn} {FR , Mo}
平衡条件：FR 0 Mo 0
l5
•等效力系(equivalent force system): 对同一刚体产生相同作用效果的力系. Fn
F3
{F1, F2 ,, Fn} {P1, P2 ,, Pm} F1
F2
{F1, F2 ,, Fn} {FR}
Pm
P2 •合力(resultant force) ：与某力系等效的力
P1
FR 称为该力系的合力，Fi（i=1,2,…n)称为合力的分力
R
F
Mr o
F
s
2020/10/18
13
BUAA
x
lM
y
约束的分类
x
l
M
y
xA A xA sin t
x
y
M
x2 y2 l2
x2 y2 l2
(x sin t)2 y2 l2
•双面约束:约束方程为等式的约束 •单面约束:约束方程为不等式的约束
•定常约束:约束方程中不显含时间t 的约束
•非定常约束:约束方程中显含时间t 的约束
FR 0, MO 0
平衡
n
n
FR Fi ' Fi
FR ( Fx )2 ( Fy )2 ( Fz )2
i1
i1
n
n
MO Mi ri Fi
MO ( MOx )2 ( MOy )2 ( MOz )2
i1
i1
空间任意力系的平衡条件：
FR
0
Fx 0
Fy 0
MO
2020/10/18
力螺旋
6
BUAA
一、基本概念与基本原理和定理
• 判断力系简化的最简结果的基本步骤：
– 计算力系的主矢 – 计算力系向某一点简化的主矩 – 分析主矢与主矩的几何关系
主要采用定性分析的方法
选择题１: 空间平行力系简化的最简结果可能是: A:平衡力系、B:力偶、C:合力、D:力螺旋
2020/10/18
华大学出版社
2020/10/18
2
BUAA
力学竞赛辅导
第一讲 静力学
• 静力学的基本概念与方法 • 平衡方程 • 虚位移原理 • 例题、思考题、问题（35个）
2020/10/18
3
BUAA 一、基本概念与基本原理和定理
•力系(force system): 作用在物体上的一组力 {F1, F2 ,, Fn}
思考题17：在下列图示结构中，构件AC上的D点作用有一已 知力（构件自重不计），回答上述问题。
2020/10/18
22
BUAA
静力学的思考题与例题
思考题18：下面哪些系统是可以保持平衡的结构？
A
D
A
D
B
L
L
A
(1)
F C
L
D
B
L
A
L (2)
F C
LDLeabharlann BL(3)L
2020/10/18
F C
L
B
L
(4)L
小位移。r
rA A rA
rA A rA
900 O
rB B rB
O
rB B rB
虚 1、不同瞬时或位置，虚位移不同
位 移 特
2、必须满足约束条件 3、是无限小的，不是有限位移
[rA ]AB [rB ]AB
点 4、虚位移不只有一个或一组 {rA,rB} {rA,rB}
2020/10/18
17
BUAA
F
C
L 23
BUAA
静力学的思考题与例题
A 思考题19：确定图示结构
D
中哪个二力杆受拉以及铰
链B的约束力FB的方向。
B
F
不计构件自重
L
(2)L