一般周期信号的傅立叶变换.

连续时间周期信号傅里叶级数：⎰=T dt t x Ta )(1⎰⎰--==T tTjkT tjk k dt et x Tdt et x Ta πω2)(1)(1离散时间周期信号傅里叶级数：[][]()∑∑=-=-==Nn nN jk Nn njkwk e n x Ne n x Na /2110π连续时间非周期信号的傅里叶变换：()⎰∞∞--=dt e t x jw Xjwt )(连续时间非周期信号的傅里叶反变换：()dw e jw X t x jwt ⎰∞∞-=π21)(连续时间周期信号傅里叶变换：∑+∞-∞=⎪⎪⎭⎫⎝⎛-=k k kw a jw X T 22)(πδπ连续时间周期信号傅里叶反变换：()dw e w w t x jwt ⎰∞∞--=0221)(πδπ离散时间非周期信号傅里叶变换：∑∞-∞=-=nnj e n x eX ωωj ][)(离散时间非周期信号傅里叶反变换：⎰=π2d e )(e π21][ωωωn j j X n x离散时间周期信号傅里叶变换：∑+∞-∞=-=kk k a X )(π2)e (0j ωωδω离散时间周期信号傅里叶反变换：[]ωωωδωd e n n j ⎰--=π20πl)2(π2π21][x拉普拉斯变换：()dt e t s Xst -∞∞-⎰=)(x拉普拉斯反变换：()()s j21t x j j d e s X st ⎰∞+∞-=σσπZ 变换：∑∞-∞=-=nnz n x X ][)z (Z 反变换： ⎰⎰-==z z z X r z X n x n nd )(πj21d )e ()(π21][1j π2ωω。

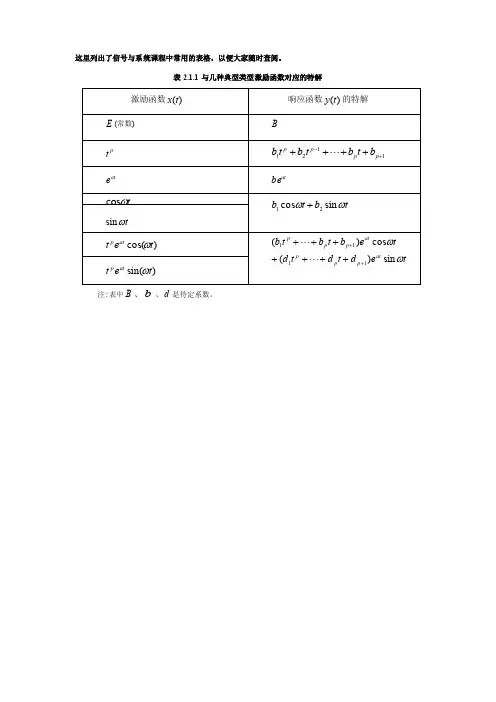
这里列出了信号与系统课程中常用的表格，以便大家随时查阅。

表2.1.1 与几种典型类型激励函数对应的特解激励函数)(t x 响应函数)(t y 的特解E (常数) Bp t 1121+-++++p p p p b t b t b t bat eat bet ωcost ωsint b t b ωωsin cos 21+)cos(t e t at p ω )sin(t e t atpωte d t d t d t e b t b t b atp p pat p p p ωωsin )(cos )(1111+++++++++注:表中B 、b 、d 是待定系数。

表3.2.1 常用周期信号的傅里叶级数系数表02T πω⎛⎫= ⎪⎝⎭01a π=02a π=a 02T πω⎛⎫= ⎪⎝⎭002sin 2n a Tn a n τωππ=⎛⎫⎪⎝⎭=()020202sin 440n a T n Ta nb τωπτπ=⎛⎫ ⎪⎝⎭==012a =表3.3.1 常用信号的傅里叶变换序号名称时间表示式()x t傅里叶变换(j )X ω矩形脉冲信号()()()22G t E u t u t τττ⎡⎤=+--⎢⎥⎣⎦Sa 2E ωττ⎛⎫⎪⎝⎭单边指数信号()at e u t -，0a > 1a j ω+双边指数信号,0()a tea t ->-∞<<+∞222aa ω+三角脉冲信号21202t t t τττ⎧⎛⎫-<⎪ ⎪⎪⎝⎭⎨⎪>⎪⎩2Sa 22τωτ⎛⎫⎪⎝⎭抽样脉冲信号0Sa()t ω000πωωωωω⎧<⎪⎨⎪>⎩钟形脉冲信号2t e τ⎛⎫- ⎪⎝⎭22eωτπτ⎛⎫- ⎪⎝⎭余弦脉冲信号cos 202t t t πτττ⎧<⎪⎪⎨⎪>⎪⎩2cos221ωττπωτπ⎛⎫- ⎪⎝⎭升余弦脉冲信号121cos 2202t t t πτττ⎧⎛⎫+< ⎪⎪⎪⎝⎭⎨⎪>⎪⎩2Sa 2212ωττωτπ⎛⎫⎪⎝⎭⎛⎫- ⎪⎝⎭符号函数1sgn()1t t t >⎧==⎨-<⎩ 2j ω单位冲激函数 ()t δ1直流信号12()πδω单位阶跃函数()u t 1()j πδωω+冲激偶信号 ()t δ'j ω单位斜变信号()tu t21()j πδωω'-表3.4.1 傅里叶变换性质序号 性质名称 时域频域1线性性质()()ax t by t + ()()aX j bY j ωω+2 尺度变换特性()x at ，0a ≠1||X j a a ω⎛⎫ ⎪⎝⎭3奇偶虚实性()x t 为实函数()()X j X j ωω=-()()ϕωϕω=--()()R j R j ωω=- ()()I j I j ωω=--*()()X j X j ωω-=()()x t x t =-()()x t x t =--()()X j R j ωω=，()0I j ω= ()()X j jI j ωω=，()0R j ω=()x t 为虚函数()()X j X j ωω=-()()ϕωϕω=--()()R j R j ωω=- ()()I j I j ωω=--*()()X j X j ωω-=4 时移特性 0()x t t - 0()j t X j e ωω-5 频移特性 0()j t x t e ω0[()]X j ωω-6对偶性()X jt 2()x πω- 7 时域微分特性()x t '()j X j ωω()()n x t()()n j X j ωω8时域积分特性()d tx ττ-∞⎰1()(0)()X j X j ωπδωω+ 9 频域微分特性()jtx t -()dX j d ωω()nt x t()n nnd X j jd ωω 10 频域积分特性()(0)()x t x t jtπδ+- ()X j d ωττ-∞⎰11 时域卷积特性 ()()12x t x t * ()()12X j X j ωω⋅12 频域卷积特性 12()()x t x t ⋅121()()2X j X j ωωπ* 13帕塞瓦尔定理221|()||()|2x t dt X j d ωωπ+∞+∞-∞-∞=⎰⎰表3.5.1 常见周期信号的傅里叶变换序号 信号名称 时间函数()x t傅里叶变换()X j ω1 虚指数信号（一） 0j t e ω 02()πδωω-2 虚指数信号（二） 0j t e ω-02()πδωω+3 余弦信号 0cos t ω ()()00ππδωωδωω++- 4正弦信号0sin t ω()()00ππj j δωωδωω--++ 5 冲激序列()()T n t t nT δδ∞=-∞=-∑()()000n n ωδωωδωω∞=-∞=-∑，02T πω= 6 一般周期信号0jn tn n X eω∞=-∞∑()()000n n ωδωωδωω∞=-∞=-∑，02Tπω=表4.1.1 常用信号的拉氏变换序号 单边信号()x t拉氏变换1 ()t δ12 ()()n t δ（n 是正整数）n s3 ()u t1s 4()t e u t α- 1s α+ 50j ()t e u t ω± 01s j ω6()n t u t （n 是正整数）1!n n s + 70sin ()tu t ω220s ωω+80cos ()tu t ω220ss ω+90sin ()tetu t αω-()022s ωαω++ 100cos ()tu t ω()22s s ααω+++11()tte u t α-()21s α+12()n t t e u t α-（n 是正整数）()1!n n s α++表4.2.1 拉普拉斯变换性质（定理）序号 性质名称 时域s 域1 线性 1122()()K x t K x t + 1122()()K X s K X s +2 时移特性 00()()x t t u t t --0()e st X s -3s 域平移特性()e αt x t -()X s α+4 时域微分特性d ()d x t t()(0)sX s x --d ()d n x t t11()0()(0)n nn r r r s X s s x ----=-∑5时域积分特性()d tx ττ-∞⎰()1(0)()x X s s s--+()()d ntx ττ-∞⎰()11(0)()in n n i i x X s s s ---+=+∑ 6s 域微分特性()tx td ()d X s s-()nt x td ()(1)d n nn X s s-7s 域积分特性()x t t ()d sX s s ∞⎰8尺度变换特性()x at1s X a a ⎛⎫ ⎪⎝⎭9 初值定理 0lim ()(0)lim ()t s x t x sX s ++→→∞==10 终值定理 0lim ()lim ()t s x t sX s →∞→=11时域卷积定理12()()x t x t * 12()()X s X t ⋅12s 域卷积定理12()()x t x t ⋅121()()2jX s X s π*表4.6.1 极点分布与原函数波形对应（1）表4.6.2 极点分布与原函数波形对应（2）表6.4.1 几种典型的激励函数所对应的特解函数式序号激励函数)(n x强迫响应)(n y p 的形式1 0B (常数)1B (常数)2 n a n Ba3 )cos(n ω )cos(θω+n B4 )sin(n ω )sin(θω+n B5 n ωj e n B ωj e6 p n p p n B n B B +++ 10 7n p a n)(10p p n n B n B B a +++8*n a （a 是特征方程的一个p 重根）p n表7.1.1 序列的形式与z 变换收敛域的关系表7.1.2 常用序列的z 变换及其收敛域序 列 z 变 换收 敛 域 )(n δ1全部z)(n u 1111--=-z z z 1>z)1(--n u1111---=--z z z1<z )(n u a n 111--=-az a z zaz >)1(--n u a n111---=--az a z za z < )(n R N1111)1(1-----=--z z z z z NN N0>z)(n nu2112)1()1(---=-z z z z1>z )(n u na n 2112)1()(---=-az z a z z az >)1(--n u na n2112)1()(----=--az az a z az a z <)(0n u e jn Ω- 10011-Ω-Ω--=-z e e z z j j1>z )()sin(0n u n Ω20101cos 21sin ---+Ω-Ωz z z1>z)()cos(0n u n Ω20101cos 21cos 1---+Ω-Ω-z z z1>z)()sin(0n u n e an Ω-aa e z z e z 220101cos 21sin -----+Ω-Ωae z ->)()cos(0n u n eanΩ-a a e z z e z 220101cos 21cos -----+Ω-Ωa e z ->)()sin(0n u n θ+Ω1cos 2)sin(sin 0202+Ω--Ω+z z z z θθ1>z )()1(n u a n n+2122)1(1)(--=-az a z za z >)(!2)2)(1(n u a n n n++3133)1(1)(--=-az a z zaz >)(!)()2)(1(n u a m m n n n n+++)1(1)1()1()1(1)(+-++-=-m m m az a z zaz >表7.3.1 z 变换的主要性质1)(n x )(z X +-<<x x R z R 2)(n h)(z H+-<<h h R z R表7.5.1 序列傅里叶变换的性质序列傅里叶变换)(n x()j X e Ω )(n y()j Y e Ω)()(n by n ax +()()j j aX e bY e ΩΩ+,a 、b 为常数3)()(n bh n ax + )()(z bH z aX +],min[],max[++--<<h x h x R R z R R 4)(m n x -)(z X z m -+-<<x x R z R 5 )(n x a n )(a zX +-<<x x R a z R a 6 )(n x n m )()(z X dzdz m -+-<<x x R z R 7 )(n x *)(**z X+-<<x x R z R8 )(n x -)1(z X -+<<x x R z R 119 )(n x -*)1(**z X-+<<x x R z R 1110 )]([n x R e)]()([21**+z X z X +-<<x x R z R 11)](Im[n x j)]()([21**-z X z X +-<<x x R z R12∑=nm m x 0)()(1z X z z- )(],1,max[n x R z x ->因果序列13)()(n h n x *)()(z H z X],min[],max[++--<<h x h x R R z R R14)()(n h n x ⎰-c dv v vz H v X j 1)()(21π ++--<<h x h x R R z R R15)(lim )0(z X x z ∞→=)(n x 为因果序列，->x R z16)()1(lim )(1z X z x z -=∞→)(n x 为因果序列，)(z X 的极点落于单位圆内部，最多在1=z 处有一极点。

常见信号的傅里叶变换信号处理领域中，傅里叶变换是一种非常重要且常见的数学工具，用来分析信号的频谱特性。

在这篇文章中，我们将介绍几种常见信号的傅里叶变换，包括方波信号、三角波信号、和正弦信号。

方波信号是一种周期性的信号，其波形呈现为由两个值交替组成的矩形波形。

对方波信号进行傅里叶变换，可以得到其频谱是一系列的奇次谐波分量。

这是因为方波信号的波形是对称的，只包含奇次谐波成分。

这种频谱特性在频域滤波和频率分析中具有重要意义。

三角波信号是一种周期性的信号，其波形呈现为由线性递增或递减的三角形波形。

对三角波信号进行傅里叶变换，可以得到其频谱是一系列的奇次和偶次谐波分量。

与方波信号不同的是，三角波信号的波形是非对称的，同时包含奇次和偶次谐波成分。

这种频谱特性在频域滤波和信号合成中也有广泛的应用。

正弦信号是一种最简单的周期性信号，其波形呈现为正弦曲线。

对正弦信号进行傅里叶变换，可以得到其频谱是一个单一的谐波分量。

这是因为正弦信号的波形是最简单的周期性波形，只包含一个频率的谐波成分。

正弦信号的频谱特性在频域滤波、频率调制和解调等领域具有重要意义。

除了这三种常见信号外，还有许多其他类型的信号可以进行傅里叶变换分析，如方波信号的卷积、正弦信号的调幅调频等。

通过对信号的傅里叶变换分析，我们可以更深入地了解信号的频谱特性，进而实现信号的处理和分析。

总的来说，傅里叶变换是信号处理领域中一种非常重要的数学工具，对于分析各种类型的信号具有重要意义。

通过对常见信号的傅里叶变换分析，我们可以更好地理解信号的频谱特性，为信号处理和分析提供更加深入的理论基础。

希望本文对读者有所启发，让大家对傅里叶变换有更深入的理解和应用。