holos旋转坐标系
- 格式:ppt
- 大小:1.46 MB
- 文档页数:3

空间直角坐标转换高斯坐标-概述说明以及解释1.引言1.1 概述概述空间直角坐标转换高斯坐标是地理信息系统中常用的一种坐标转换方式。
在许多地理测量与测绘应用中,我们需要将空间直角坐标系统与高斯坐标系统进行转换,以适应不同需求。
本文将探讨空间直角坐标转换为高斯坐标的方法,以及其应用和意义。
空间直角坐标系统是一种直角坐标系,常用于地理测量与测绘领域。
它由三个坐标轴(通常为X、Y和Z轴)组成,分别表示了物体在水平面和垂直方向上的位置。
这种坐标系统简单明了,计算方便,广泛应用于地理信息系统、建筑设计、航空航天等领域。
然而,在一些特定的测量工作中,空间直角坐标系统的局限性逐渐显现出来。
例如,当我们需要进行大范围地理测量或测绘时,空间直角坐标往往不能满足要求。
这时,我们就需要将其转换为高斯坐标系统。
高斯坐标系统是一种采用高斯投影的地理坐标系统,用于更精确地描述地球表面上的点位置。
相比于空间直角坐标系统,高斯坐标系统更适用于大尺度地理测量与测绘工作。
它充分考虑了地球的椭球形状和横切面的变形,使得测量结果更加准确可靠。
本文将介绍空间直角坐标转换为高斯坐标的方法,包括数学模型与计算公式。
我们将详细讨论如何根据特定的空间直角坐标值,通过计算和转换,得到对应的高斯坐标值。
同时,我们还将探讨空间直角坐标转换为高斯坐标的应用和意义。
通过实际案例和应用场景,我们将展示这种坐标转换方法在地理测量与测绘领域的重要作用。
在文章的后续部分,我们将进一步探讨空间直角坐标转换为高斯坐标的具体步骤和注意事项。
同时,我们将讨论该转换方法的优势和适用性,以及可能存在的问题和局限性。
通过深入剖析空间直角坐标转换高斯坐标的理论与实践,我们旨在为读者提供一种有效的坐标转换工具,并拓宽他们对地理信息系统的认识和应用领域的理解。
1.2文章结构文章结构将按照以下顺序进行展开:1. 引言1.1 概述1.2 文章结构1.3 目的2. 正文2.1 空间直角坐标系统2.2 高斯坐标系统3. 结论3.1 空间直角坐标转换为高斯坐标的方法3.2 应用和意义在本文中,我将首先给出对空间直角坐标系统和高斯坐标系统的简单介绍。

A r c G I S中的坐标系定义与转换ArcGIS中的坐标系定义与转换2009-06-23 15:481.椭球体、基准面及地图投影GIS中的坐标系定义由基准面和地图投影两组参数确定,而基准面的定义则由特定椭球体及其对应的转换参数确定,因此欲正确定义GIS系统坐标系,首先必须弄清地球椭球体(Ellipsoid)、大地基准面(Datum)及地图投影(Projection)三者的基本概念及它们之间的关系。
基准面是利用特定椭球体对特定地区地球表面的逼近,因此每个国家或地区均有各自的基准面,我们通常称谓的北京54坐标系、西安80坐标系实际上指的是我国的两个大地基准面。
我国参照前苏联从1953年起采用克拉索夫斯基(Krassovsky)椭球体建立了我国的北京54坐标系,1978年采用国际大地测量协会推荐的1975地球椭球体建立了西安80坐标系,目前大地测量基本上仍以北京54坐标系作为参照,北京54与西安80坐标之间的转换可查阅国家测绘局公布的对照表。
WGS1984基准面采用WGS84椭球体,它是一地心坐标系,即以地心作为椭球体中心,目前GPS测量数据多以WGS1984为基准。
地理坐标:为球面坐标。
参考平面地是椭球面。
坐标单位:经纬度大地坐标:为平面坐标。
参考平面地是水平面。
坐标单位:米、千米等。
地理坐标转换到大地坐标的过程可理解为投影。
(投影:将不规则的地球曲面转换为平面)在ArcGIS中预定义了两套坐标系:地理坐标系(Geographic coordinate system)和投影坐标系(Projected coordinate system),1、首先理解地理坐标系(Geographic coordinate system),是以经纬度为地图的存储单位的。
很明显,Geographic coordinate system是球面坐标系统。
我们要将地球上的数字化信息存放到球面坐标系统上,如何进行操作呢?地球是一个不规则的椭球,如何将数据信息以科学的方法存放到椭球上?这必然要求我们找到这样的一个椭球体。

arx 旋转坐标系-回复旋转坐标系是一种数学概念,在几何学和物理学中被广泛应用。
它是一种坐标系统转换方法,可以将一个坐标系中的点的坐标转换为另一个坐标系中的点的坐标,使得在新的坐标系中,原来的点的位置和方向发生了改变。
本文将详细介绍旋转坐标系的概念、原理以及旋转坐标系的运用。
一、旋转坐标系的概念旋转坐标系是一种由两个坐标轴组成的坐标系,这两个坐标轴之间存在一定的夹角。
通过旋转坐标系,原坐标系中的点的坐标可以转换为新坐标系中的点的坐标,同时也可以将新坐标系中的点的坐标转换为原坐标系中的点的坐标。
旋转坐标系能够将坐标系中的点的位置和方向进行变换,使得原来的点在新坐标系中的位置和方向发生改变。
二、旋转坐标系的原理旋转坐标系的转换是通过旋转矩阵来实现的。
旋转矩阵是一个二维或三维方阵,用于描述旋转坐标系中的点的转换关系。
在二维情况下,旋转矩阵如下所示:R = [cosθ-sinθ][sinθcosθ],其中,θ表示旋转的角度。
在三维情况下,旋转矩阵的形式较复杂,它可以通过旋转轴和旋转角度来确定。
旋转矩阵可以通过矩阵乘法将原坐标系中的点的坐标转换为新坐标系中的点的坐标。
即新坐标系中的点的坐标可以表示为:[x'][y'][z'] = R * [x][y][z],其中,[x, y, z]表示原坐标系中的点的坐标,[x', y', z']表示新坐标系中的点的坐标,R表示旋转矩阵。
三、旋转坐标系的运用旋转坐标系的运用非常广泛,可以应用于众多领域。
在几何学中,旋转坐标系被用于研究图形的旋转、变换和对称性。
在物理学中,旋转坐标系被用于描述物体的运动、力的作用方向等。
以下将分别介绍旋转坐标系在几何学和物理学中的运用。
1. 几何学中的运用旋转坐标系可以用于图形的旋转。
通过将坐标轴旋转一定角度,可以实现对图形的任意旋转。
这在计算机图形学中非常重要,用于实现图形的旋转变换,使图形在屏幕上呈现出不同的角度和方向。

arx 旋转坐标系-回复什么是旋转坐标系?如何进行坐标系的旋转操作?旋转坐标系有什么实际应用?本文将一步一步回答这些问题。
旋转坐标系是一种数学工具,用于将一个坐标系在平面上旋转一定角度,从而改变坐标轴的方向和位置。
通过旋转坐标系,我们可以将任意点的坐标转换到新的坐标系中,并在新坐标系中进行运算和分析。
进行坐标系旋转操作需要以下步骤:第一步:确定旋转角度和旋转中心。
旋转角度表示坐标系相对于原始坐标系的旋转角度,可以用逆时针方向表示。
旋转中心表示旋转的中心点,可以是坐标系的原点或其他指定点。
第二步:绘制旋转向量。
旋转向量是指从原点到某一点的向量,例如表示旋转中心和任意一点间的向量。
第三步:计算旋转后的新坐标系。
根据旋转中心和旋转向量,可以计算出旋转后的新坐标系的新坐标轴方向。
第四步:将原始坐标系上的点转换到新坐标系中。
通过旋转矩阵的运算,可以将坐标系内的点从原始坐标系转换到新坐标系中,从而得到点在新坐标系中的坐标。
旋转坐标系的应用非常广泛。
以下是一些实际应用的示例:1. 机器人运动控制:在机器人控制中,通过旋转坐标系可以使机器人移动相对于旋转中心的指定角度和方向,从而实现精确的运动路径规划。
2. 图像处理:在图像处理中,旋转坐标系可用于图像变换和特征提取。
通过旋转坐标系,可以将图像中的对象对齐到水平或垂直方向,便于后续的图像处理和分析。
3. 三维建模:在三维建模中,旋转坐标系可用于旋转物体或相机视角,实现不同角度的展示和渲染。
4. 飞行器导航:在飞行器导航中,通过旋转坐标系可以使飞行器调整姿态,以适应不同的飞行任务和场景要求。
5. 天文学研究:在天文学中,旋转坐标系可用于表示天体的运动和观测位置,以研究星系、行星和恒星等天体的运动规律。
总结起来,旋转坐标系是一种强大的数学工具,能够改变坐标轴的方向和位置,有广泛的实际应用。
通过旋转坐标系,我们可以在新的坐标系中进行运算和分析,从而更好地理解和应用数学知识。

立式加工中心培训资料2007 年5 月VF系列操作人员手册内容目录安全 (1)操作⋯⋯⋯ (4)基本介绍⋯⋯⋯⋯⋯⋯⋯ (4)坐标体系⋯ (4)绝对定位法和增量定位 (5)用代码编程 (5)机床缺省值 (5)程序格式 (6)固定循环 (7)刀具交换装置安装步骤..................................... . (8)操作员控制面板 (9)实时计时器 (12)键盘 (12)通电/断电⋯⋯⋯ (20)手动操作⋯⋯ (20)自动操作⋯⋯⋯ (21)创建、编辑和保存程序 (23)程序输入/输出⋯ (26)试运行操作 (30)显示 (30)行程限制⋯⋯⋯⋯⋯⋯ (44)运行-停止-轻推-继续 (45)编程⋯⋯ (46)工作坐标系统 (46)编程结构 (46)字母地址代码 (48)技巧与窍门 (51)高速机械加工(可选) (61)第4轴编程 (62)子程序 (65)刀具功能(Tnn) (73)侧挂式刀具交换装置 (74)用VF系统计算机数控铣床攻丝............................ . (83)铣刀补偿 (86)高级编辑 (98)G代码(预备功能) (105)M代码(各种功能) (151)设置 (160)在工作中不要发生这种情况所有的铣削设备如旋转件、皮带、滑轮、高压电、噪音、压缩空气等均有危险存在,所以在使用CNC备及其组件时,为避免人身伤害及机械损坏,必严格遵守相应的安全守则。
操作安全必读‹ 只有经过授权的人员方可使用本机,未经培训人员在使用机床时可能对人身及机床造成伤害以及由于不正确的操作造成的问题不属保修范围内。
‹ 操作前请认真检查零配件及刀具,所有损坏的配件和刀具应当由专业人员修理或替换。
一旦有部件显示异常,不要操作,应及时联系您的车间质检人员。
‹ 操作机床时使用合适的眼、耳保护装置。
推荐使用ANSI认证的护目镜和OSHA认证的耳罩。
‹ 操作机床时一定确保其门关闭,门已正确互锁,旋转的刀具可能造成严重的人身伤害,当程序在运行中时,机床平台及主轴头能够在任一时间向任一方向做非常快的移动。
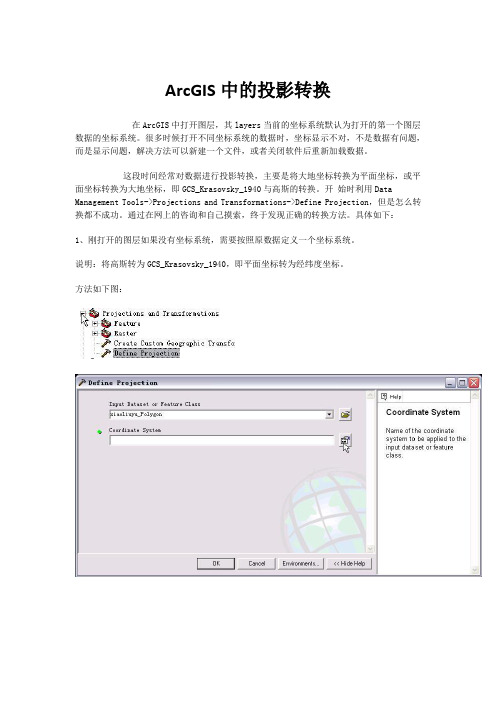
ArcGIS中的投影转换在ArcGIS中打开图层,其layers当前的坐标系统默认为打开的第一个图层数据的坐标系统。
很多时候打开不同坐标系统的数据时,坐标显示不对,不是数据有问题,而是显示问题,解决方法可以新建一个文件,或者关闭软件后重新加载数据。
这段时间经常对数据进行投影转换,主要是将大地坐标转换为平面坐标,或平面坐标转换为大地坐标,即GCS_Krasovsky_1940与高斯的转换。
开始时利用Data Management Tools->Projections and Transformations->Define Projection,但是怎么转换都不成功。
通过在网上的咨询和自己摸索,终于发现正确的转换方法。
具体如下:1、刚打开的图层如果没有坐标系统,需要按照原数据定义一个坐标系统。
说明:将高斯转为GCS_Krasovsky_1940,即平面坐标转为经纬度坐标。
方法如下图:2、再进行投影转换,方法如下图:上面是当数据本身没有坐标系统时的做法,如果不知道原来是什么投影,指定了高斯坐标系统也还是转不过去(失败,为什么???)如果本身已经有坐标系统,可以从feature -》project直接转换运行ArcGIS9中的ArcMap,打开ArcToolBox,打开 Data Management Tools ->Projections and Transformations->Feature->Project 项打开投影对话框。
在Input DataSet or Feature Class栏中输入或点击旁边的按钮选择相应的DataSet或Feature Class(带有空间参考),Output DataSet or Feature Class栏中输入或点击旁边的按钮选择目标DataSet 或Feature Class,在Output Coordinate System 栏中输入或点击旁边的按钮选择目标数据的坐标系统。
arx 旋转坐标系-回复什么是旋转坐标系?如何进行旋转坐标系转换?旋转坐标系有何应用?在本文中,我们将一步一步回答这些问题,并深入探讨旋转坐标系的原理和应用。
首先,我们来搞清楚什么是旋转坐标系。
在数学和物理学中,坐标系是用来描述空间中点的位置和方向的工具。
通常,我们使用笛卡尔坐标系,也称为直角坐标系。
在笛卡尔坐标系中,我们用三个坐标轴(通常是x,y,z轴)来确定一个点的位置。
然而,在某些情况下,使用笛卡尔坐标系可能不够方便或有效。
这时,我们可以采用旋转坐标系来描述问题。
旋转坐标系是通过旋转笛卡尔坐标系中的坐标轴来改变坐标系的方向和位置。
通过旋转坐标系,我们可以将原始坐标系中的问题转化为在旋转坐标系中更容易解决的问题。
接下来,我们将介绍旋转坐标系的转换方法。
旋转坐标系的转换涉及到旋转矩阵和坐标变换矩阵的使用。
首先,我们需要确定旋转坐标系相对于原始坐标系的旋转角度和旋转轴。
旋转角度用θ表示,旋转轴用单位向量u表示。
然后,我们可以构造一个3×3的旋转矩阵R来表示坐标轴的旋转。
旋转矩阵R的每一列都是旋转后的坐标轴在原始坐标系中的坐标。
为了将一个点的坐标从原始坐标系转换到旋转坐标系中,我们需要使用一个3×3的坐标变换矩阵T。
坐标变换矩阵T是旋转矩阵R的逆矩阵。
给定一个点的坐标P在原始坐标系中,我们可以使用如下的公式转换该点在旋转坐标系中的坐标Q:Q = T ×P其中,P和Q都表示点的坐标的列向量。
现在,我们来看一些旋转坐标系的具体应用。
在物理学中,旋转坐标系广泛应用于描述刚体的运动。
通过旋转坐标系的转换,我们可以简化刚体的运动方程,并更好地描述其运动状态。
在机器人学中,旋转坐标系被用于描述机器人的姿态和运动。
通过旋转坐标系的变换,我们可以将机器人的控制问题转化为在旋转坐标系中更容易解决的问题,从而实现更高效的控制和规划。
此外,在计算机图形学和计算机视觉领域,旋转坐标系也被广泛应用。
Arx旋转坐标系Arx旋转坐标系是一种常用的三维坐标系转换方法,它可以将一个物体从一个坐标系旋转到另一个坐标系。
在三维建模、机器人学、计算机图形学等领域中,经常需要使用Arx旋转坐标系来进行坐标变换。
一、Arx旋转坐标系的定义Arx旋转坐标系以原点O为中心,通过三个互相垂直的平面来确定一个三维空间的坐标系。
这三个平面分别为:X平面、Y平面和Z平面。
每个平面上都有一个单位向量,分别表示为i、j、k,其中i为X轴上的单位向量,j为Y轴上的单位向量,k为Z轴上的单位向量。
Arx旋转坐标系的旋转矩阵可以表示为:[cos(a) -sin(a) 0][sin(a) cos(a) 0][0 0 1]其中a为绕Z轴旋转的角度。
当a=0时,表示没有旋转;当a>0时,表示逆时针旋转;当a<0时,表示顺时针旋转。
通过连续应用Arx旋转坐标系的旋转矩阵,可以将一个物体从一个坐标系旋转到另一个坐标系。
二、Arx旋转坐标系的优点1.简单易用:Arx旋转坐标系的定义简单明了,易于理解和实现。
2.灵活性高:Arx旋转坐标系可以通过连续应用旋转矩阵来实现任意角度的旋转,具有很高的灵活性。
3.物理意义明确:Arx旋转坐标系的旋转矩阵具有明确的物理意义,易于与实际物理系统进行关联。
4.应用广泛:Arx旋转坐标系在三维建模、机器人学、计算机图形学等领域中广泛应用。
三、Arx旋转坐标系的实现方式Arx旋转坐标系的实现方式有多种,以下是一种常见的实现方式:1.定义原点O和三个单位向量i、j、k。
2.定义绕Z轴的旋转角度a。
3.根据Arx旋转坐标系的旋转矩阵计算新的坐标值。
具体计算过程可以根据需要选择不同的方式进行,例如可以通过矩阵乘法或者直接替换变量等方式进行计算。
4.应用新的坐标值更新物体的位置和姿态。
四、总结Arx旋转坐标系是一种简单易用、灵活性高、物理意义明确的坐标系转换方法,在三维建模、机器人学、计算机图形学等领域中广泛应用。
geometrydescriptor geometry 转换坐标系-回复如何将Geometry对象的坐标系转换。
步骤1:理解坐标系转换的概念在进行坐标系转换之前,我们首先需要了解什么是坐标系转换。
坐标系是一种用于描述和表示地理空间位置的系统。
不同的坐标系采用不同的参考点和度量单位。
坐标系转换是将一个Geometry对象从一个坐标系转换到另一个坐标系。
这种转换通常是为了在不同的GIS应用程序之间共享地理数据,或者在不同的坐标系下进行地理空间分析。
步骤2:确定源和目标坐标系在进行坐标系转换之前,我们需要确定源Geometry对象的坐标系和目标坐标系。
源坐标系是Geometry对象当前所在的坐标系,而目标坐标系是我们希望将Geometry对象转换到的坐标系。
源和目标坐标系通常由坐标参考系统(CRS)或坐标参考标识(CRS ID)表示。
步骤3:获取源Geometry对象的CRS信息在进行坐标系转换之前,我们需要获取源Geometry对象的坐标参考系统(CRS)信息。
CRS信息通常包括坐标系的名称、坐标系的地理范围、坐标系的投影信息等。
根据不同的GIS应用程序,获取CRS信息的方法可能会有所不同。
一种常见的方法是使用Geometry对象的metadata属性来获取CRS信息。
步骤4:确定源坐标系和目标坐标系的转换关系确定源坐标系和目标坐标系的转换关系是进行坐标系转换的关键步骤。
不同的坐标系转换方法和工具可能会采用不同的转换关系。
常见的转换关系包括七参数转换、四参数转换、仿射转换等。
我们需要根据具体的坐标系转换要求来确定适合的转换关系。
步骤5:使用合适的工具进行坐标系转换根据源坐标系和目标坐标系的转换关系,我们可以选择合适的工具或库来进行坐标系转换。
常用的工具包括GDAL、Proj4、ArcGIS等。
以下是一些常见的坐标系转换工具的使用示例:- GDAL:Pythonimport gdal# 读取源Geometry对象src_geom = ogr.CreateGeometryFromWkt('POINT(10 20)')# 源坐标系和目标坐标系的CRS信息src_crs = osr.SpatialReference()src_crs.ImportFromEPSG(4326) # EPSG code for WGS84tar_crs = osr.SpatialReference()tar_crs.ImportFromEPSG(3857) # EPSG code for Web Mercator# 坐标系转换transform = osr.CoordinateTransformation(src_crs, tar_crs)src_geom.Transform(transform)# 输出转换后的Geometry对象print(src_geom.ExportToWkt())- Proj4:Pythonfrom pyproj import Proj, transform# 源坐标系和目标坐标系的proj4字符串src_crs = Proj('+proj=longlat +datum=WGS84 +no_defs')tar_crs = Proj('+proj=utm +zone=33 +datum=WGS84 +units=m +no_defs')# 源Geometry对象src_geom = shapely.geometry.Point(10, 20)# 坐标系转换x, y = transform(src_crs, tar_crs, src_geom.x, src_geom.y)# 输出转换后的Geometry对象print(shapely.geometry.Point(x, y))- ArcGIS:使用ArcPy模块提供的功能进行坐标系转换,具体代码可以根据ArcPy 的文档进行选择和调整。