球坐标系,三位坐标变换,旋转
- 格式:doc
- 大小:84.50 KB
- 文档页数:2
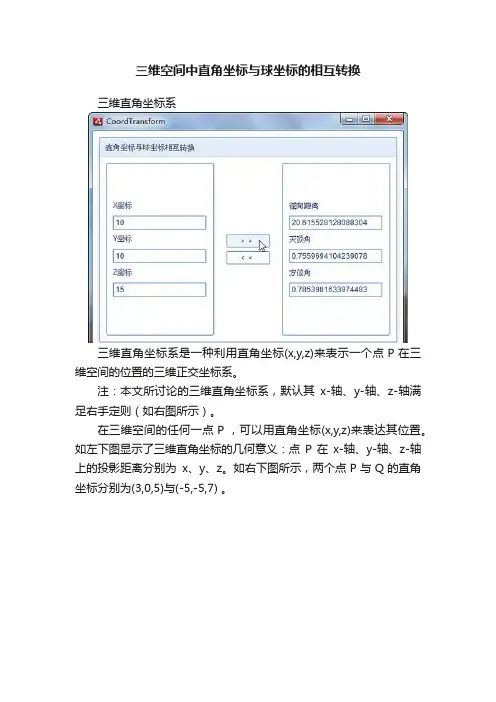
三维空间中直角坐标与球坐标的相互转换三维直角坐标系三维直角坐标系是一种利用直角坐标(x,y,z)来表示一个点 P 在三维空间的位置的三维正交坐标系。
注:本文所讨论的三维直角坐标系,默认其x-轴、y-轴、z-轴满足右手定则(如右图所示)。
在三维空间的任何一点 P ,可以用直角坐标(x,y,z)来表达其位置。
如左下图显示了三维直角坐标的几何意义:点P在x-轴、y-轴、z-轴上的投影距离分别为x、y、z。
如右下图所示,两个点 P 与 Q 的直角坐标分别为(3,0,5)与(-5,-5,7) 。
球坐标系球坐标系是一种利用球坐标(r, , )来表示一个点 P 在三维空间的位置的三维正交坐标系。
下图描述了球坐标的几何意义:原点O与目标点P之间的径向距离为r,O到P的连线与正z-轴之间的夹角为天顶角,O到P的连线在xy-平面上的投影线与正x-轴之间的夹角为方位角。
假设 P 点在三维空间的位置的三个坐标是。
那么, 0 r 是从原点到 P 点的距离, 0 是从原点到 P 点的连线与正 z-轴的夹角, 0 <>时,与都一起失去意义。
当或时,失去意义。
三维空间下直角坐标与球坐标的相互转换直接坐标转球坐标、、。
球坐标转直角坐标、、。
基于Flex的坐标转换实现直角坐标定义类CartesianCoord.cs package hans_gis.coord{public class CartesianCoord{public var x:Number;public var y:Number;public var z:Number;static private var temp:CartesianCoord = CartesianCoord.ZE RO;public function CartesianCoord(x:Number=0, y:Number=0, z:Number=0){this.x = x;this.y = y;this.z = z;}public function clone():CartesianCoord{return new CartesianCoord(this.x, this.y, this.z);}public function copyTo(n:CartesianCoord):void{n.x = this.x;n.y = this.y;n.z = this.z;}public function copyFrom(n:CartesianCoord):void{this.x = n.x;this.y = n.y;this.z = n.z;}public function reset(newx:Number = 0, newy:Number = 0, newz:Number = 0):void{this.x = newx;this.y = newy;this.z = newz;}static public function get ZERO():CartesianCoord{return new CartesianCoord(0, 0, 0);}}}球坐标定义类SphericalCoord.cspackage hans_gis.coord{public class SphericalCoord{public var radius:Number;public var theta:Number;public var phi:Number;static private var temp:SphericalCoord = SphericalCoord.ZE RO;public function SphericalCoord(radius:Number=0, theta:Nu mber=0, phi:Number=0){this.radius = radius;this.theta = theta;this.phi = phi;}public function clone():SphericalCoord{return new SphericalCoord(this.radius, this.theta, this.phi);}public function copyTo(n:SphericalCoord):void{n.radius = this.radius;n.theta = this.theta;n.phi = this.phi;}public function copyFrom(n:SphericalCoord):void{this.radius = n.radius;this.theta = n.theta;this.phi = n.phi;}public function reset(newradius:Number = 0, newtheta:Nu mber = 0, newphi:Number = 0):void{this.radius = newradius;this.theta = newtheta;this.phi = newphi;}static public function get ZERO():SphericalCoord{return new SphericalCoord(0, 0, 0);}}}坐标转换定义类CoordsTransform.cspackage hans_gis.coord{public class CoordsTransform{public function CoordsTransform(){}public function CartesianT oSpherical(coord:CartesianCoord): SphericalCoord{var radius = this.GetModuloFromCartesianCoord(coord);var theta = this.GetThetaFromCartesianCoord(coord);var phi = this.GetPhiFromCartesianCoord(coord);return new SphericalCoord(radius, theta, phi);}protected function GetModuloFromCartesianCoord(coord:C artesianCoord):Number{return Math.sqrt( coord.x*coord.x + coord.y*coord.y + coor d.z*coord.z );}protected function GetThetaFromCartesianCoord(coord:Car tesianCoord):Number{// return Math.atan(Math.sqrt(coord.x*coord.x + coord.y*co ord.y)/coord.z);return Math.acos(coord.z/this.GetModuloFromCartesianCoo rd(coord));}protected function GetPhiFromCartesianCoord(coord:Cartes ianCoord):Number{return Math.atan(coord.y/coord.x);}public function SphericalToCartesian(coord:SphericalCoord): CartesianCoord{var x = this.GetXFromSphericalCoord(coord);var y = this.GetYFromSphericalCoord(coord);var z = this.GetZFromSphericalCoord(coord);return new CartesianCoord(x, y, z);}protected function GetXFromSphericalCoord(coord:Spheric alCoord):Number{return coord.radius*Math.sin(coord.theta)*Math.cos(coord.p hi);}protected function GetYFromSphericalCoord(coord:Spherica lCoord):Number{return coord.radius*Math.sin(coord.theta)*Math.sin(coord.p hi);}protected function GetZFromSphericalCoord(coord:Spherica lCoord):Number{return coord.radius*Math.cos(coord.theta);}}}实例运行结果附:实例下载。

坐标系转换方法和技巧1.二维坐标系转换:二维坐标系转换是将平面上的点从一个坐标系转换到另一个坐标系中。
常用的方法有旋转、平移和缩放。
-旋转:通过改变坐标系的旋转角度,可以将点从一个坐标系转换到另一个坐标系。
-平移:通过改变坐标系的平移量,可以将点从一个坐标系平移到另一个坐标系。
-缩放:通过改变坐标系的比例尺,可以将点从一个坐标系缩放到另一个坐标系。
2.三维坐标系转换:三维坐标系转换是将空间中的点从一个坐标系转换到另一个坐标系中。
常用的方法有旋转、平移和缩放。
-旋转:通过改变坐标系的旋转角度,可以将点从一个坐标系转换到另一个坐标系。
-平移:通过改变坐标系的平移量,可以将点从一个坐标系平移到另一个坐标系。
-缩放:通过改变坐标系的比例尺,可以将点从一个坐标系缩放到另一个坐标系。
3.地理坐标系转换:地理坐标系转换是将地球表面点的经纬度坐标转换为平面坐标系(如UTM坐标系)或其他地理坐标系中的点。
常用的方法有投影转换和大地坐标转换。
-投影转换:根据不同的地理投影模型,将地理坐标系中的点投影到平面上。
常用的地理投影包括墨卡托投影、兰伯特投影等。
-大地坐标转换:根据椭球模型和大地测量的理论,将地理坐标系中的点转换为具有X、Y、Z三维坐标的点。
常见的大地坐标系包括WGS84和GCJ-02等。
4.坐标系转换的技巧:-精度控制:在坐标系转换过程中,需要注意精度的控制,以确保转换后的坐标满足要求。
-参考点选择:在坐标系转换过程中,选取合适的参考点可以提高转换的准确性和稳定性。
-坐标系转换参数的确定:在进行坐标系转换时,需要确定旋转角度、平移量和比例尺等参数,可以通过多点共面条件、最小二乘法等方法进行确定。
-转换效率优化:针对大规模的坐标系转换,可以采用分块处理、并行计算等技术来提高转换效率。
在进行坐标系转换时,需要根据具体的需求选择适当的方法和技巧,并结合具体的软件工具进行实现。
同时,还需要注意坐标系转换的精度和准确性,确保转换结果符合要求。




❝§3-1 球面坐标系、坐标变换的意义与一般公式❝§3-2 决定新极Q 的地理坐标φ0,λ0❝§3-3 地理坐标φ,λ换算为球面极坐标α,Z❝球面余弦公式Ac b c b a cos sin sin cos cos cos ⋅⋅+⋅=Cc B b A a sin sin sin sin sin sin ==Bc a c a b cos sin sin cos cos cos ⋅⋅+⋅=Cb a b ac cos sin sin cos cos cos ⋅⋅+⋅=❝球面正弦公式sinacos B =cos b sin c -sin b cos c cos A❝球面边正弦与邻角余弦之积公式球面三角形的基本公式边的余弦公式定理:球面三角形任意边的余弦等于其它两边余弦的乘积加上这两边的正弦及其夹角余弦的连乘积。
Ac b c b a cos sin sin cos cos cos +=正弦公式定理:球面三角形各边的正弦和对角的正弦成正比。
Cc B b A a sin sin sin sin sin sin ==一、球面坐标系、坐标变换为在球面上确定点位可是需要采用不同的坐标系。
制图实践中常使用的有地理坐标系(φ、λ),球面坐标系(a, z)和球面直角坐标系(x,y)。
目前以上三种坐标系在测绘技术上应用最为广泛。
三者之间可以进行简单的相互换算。
如下图,其中K 为球面上一点地理坐标为,球面极坐标为。
P 是地理坐标系极点,Q 是球面极坐标系新极点。
二、坐标变换的一般公式()λϕ,()00λϕ,()z ,α由地理坐标系到球面极坐标系之间的变换:()000cos cos cos sin sin cos λλϕϕϕϕ-+=z 在球面三角形PQA ,由边的余弦公式有:()()ϕϕ--=︒︒90cos 90cos cos 0z ()()()00cos 90sin 90sin λλϕϕ---+︒︒即式中φ0、λ0是球面坐标原点Q的地理坐标()000cos sin cos cos sin cos sin λλϕϕϕϕ--=a z )sin(cos sin sin 0λλϕ-=a z 由第一正余弦公式有()()ϕϕ--=︒︒90cos 90sin cos sin 0a z ()()()00cos 90sin 90cos λλϕϕ----︒︒即由正弦公式有()a z sin 90sin )sin(sin 0ϕλλ-=-︒由此得到:()000cos cos cos sin sin cos λλϕϕϕϕ-+=z ()()0000cos sin cos cos sin sin cos λλϕϕϕϕλλϕ---=tga由球面极坐标到地理坐标之间的变换:a z z cos sin cos cos sin sin 00ϕϕϕ+=在球面三角形PKQ ,由余弦公式有:()()zcos 90cos 90cos 0ϕϕ-=-︒︒()αϕcos sin 90sin 0z -+︒即式中φ0、λ0是球面坐标原点Q的地理坐标()αϕϕλλϕcos sin sin cos cos cos cos 000z z -=-)sin(cos sin sin 0λλϕ-=a z 由第一正余弦公式有()()()z cos 90sin cos 90sin 00ϕλλϕ-=--︒︒()αϕcos sin 90cos 0z --︒即由正弦公式有()a z sin 90sin )sin(sin 0ϕλλ-=-︒由此得到:αϕϕϕcos sin cos cos sin sin 00z z +=()zz tg sin cos sin cos cos sin cos 000αϕϕαϕλλ-=-由地理坐标到球面直角坐标间的变换:如图POP 1为中央经线,其经度为,新极点Q 位于赤道上,其经度为球面上点A 地理坐标为,,过A 点作垂直圈QAB 与中央经线交于B ,令BO=x,,BA =y 则A 的球面直角坐标为(x ,y)0λ︒+900λϕλ在球面直角三角形PBA 有()()()0cos 9090ctg ctg x λλφ︒︒-=--()()0sin 90sin sin λλϕ--=︒y 于是得到由地理坐标到球面直角坐标的变换公式为()0sec λλϕ-=tg tgx ()0sin cos sin λλϕ-=y在球面直角三角形PBA 有()()yx cos 90cos 90cos -=-︒︒ϕ()()090sin λλ-=-︒tgyctg x 于是得到yx cos sin sin =ϕ()xtgy tg sec 0=-λλ在一般情况下,大多数地图投影都采用地理坐标表示球面位置建立平面直角坐标与的关系。


三维坐标系的旋转变换三维坐标系的旋转变换是计算机图形学和几何学中一个非常重要的概念。
它能够将一个物体在三维空间中绕着指定的轴进行旋转,从而改变它相对于其他物体的位置和方向。
本文将介绍三维坐标系的旋转变换的原理、方法和应用,并提供一些指导意义的实例。
一、三维坐标系的基本概念在介绍旋转变换之前,我们先来了解一下三维坐标系的基本概念。
三维坐标系由三个相互垂直的坐标轴组成:X轴、Y轴和Z轴。
X轴代表左右方向,Y轴代表前后方向,Z轴代表上下方向。
每个点在三维空间中都可以由三个坐标值来表示,分别表示其在X轴、Y轴和Z轴上的位置。
二、旋转变换的原理旋转变换是通过改变坐标系的方向和角度来实现的。
在三维坐标系中,我们可以选择一条旋转轴,将其视为一个固定不动的轴,然后将其他点围绕着这个轴进行旋转。
旋转角度可以是正数(顺时针方向)或负数(逆时针方向),单位通常是弧度或角度。
三、旋转变换的方法通过旋转变换,我们可以在三维空间中实现各种各样的变换效果,例如旋转、翻转、缩放等。
以下是几种常见的旋转变换方法:1. 绕X轴旋转:围绕X轴进行旋转变换时,我们可以通过改变Y 轴和Z轴的坐标值,来实现点在平面上的旋转效果。
2. 绕Y轴旋转:围绕Y轴进行旋转变换时,我们可以通过改变X 轴和Z轴的坐标值,来实现点在平面上的旋转效果。
3. 绕Z轴旋转:围绕Z轴进行旋转变换时,我们可以通过改变X 轴和Y轴的坐标值,来实现点在平面上的旋转效果。
四、旋转变换的应用旋转变换在计算机图形学和几何学中有广泛的应用。
它可以用来进行三维模型的角度调整,实现刚体变换,以及修正物体在三维空间中的位置和方向。
例如,在计算机游戏中,我们可以通过旋转变换来实现角色的动画效果,使其在三维空间中做出各种各样的动作。
五、旋转变换的指导意义掌握三维坐标系的旋转变换对于计算机图形学和几何学的研究和应用都非常重要。
它可以帮助我们理解和分析三维空间中的物体运动和变化,并通过数学方法实现对其的控制和调整。


圆柱坐标系与球坐标系的变换关系是什么在数学和物理学中,我们常常需要使用不同的坐标系来描述和研究问题。
其中,圆柱坐标系和球坐标系是两种常见的三维坐标系。
本文将探讨圆柱坐标系和球坐标系之间的变换关系。
圆柱坐标系圆柱坐标系是由笛卡尔坐标系(也称为直角坐标系)旋转形成的。
它可以通过给定距离原点r、极角 $\\theta$、高度z来确定空间中的一个点。
具体而言,对于一个点P,它在圆柱坐标系下的坐标为 $(r, \\theta, z)$。
其中,r表示点P到z轴的距离,$\\theta$ 表示点P在x−y平面上与x轴的夹角,以弧度为单位。
而z则表示点P在z轴上的高度。
球坐标系球坐标系是由笛卡尔坐标系旋转形成的另一种坐标系。
在球坐标系下,一个点P可以通过给定半径r、极角 $\\theta$、方位角 $\\phi$ 来描述。
具体而言,点P在球坐标系下的坐标表示为 $(r, \\theta, \\phi)$。
其中,r表示点P到原点的距离, $\\theta$ 表示点P在x−y平面上与x轴的夹角,$\\phi$ 表示点P与z轴的夹角。
圆柱坐标系到球坐标系的变换关系为了方便研究和计算,我们需要了解圆柱坐标系和球坐标系之间的变换关系。
下面给出从圆柱坐标系到球坐标系的变换公式:•$r = \\sqrt{x^2 + y^2}$•$\\theta = \\arctan\\left(\\frac{y}{x}\\right)$•$\\phi = \\arccos\\left(\\frac{z}{\\sqrt{x^2 + y^2 + z^2}}\\right)$这些变换关系可以帮助我们在两种不同的坐标系下进行问题的转化和计算。
例如,当我们在圆柱坐标系下给出一个点的坐标 $(r, \\theta, z)$,我们可以使用上述变换关系将其转换为球坐标系下的坐标 $(r', \\theta', \\phi')$。
球坐标系到圆柱坐标系的变换关系同样地,我们也可以得到从球坐标系到圆柱坐标系的变换公式,如下所示:•$r = r' \\sin \\phi'$•$\\theta = \\theta'$•$z = r' \\cos \\phi'$这些变换关系使得我们能够方便地在两种不同的坐标系之间进行转换和计算。
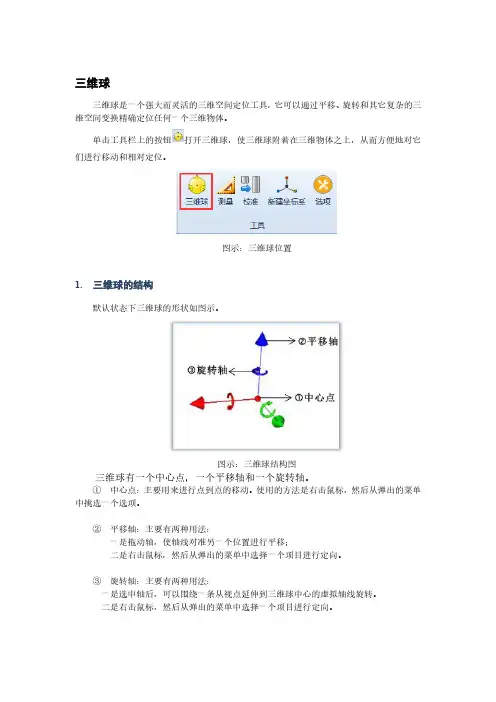
三维球三维球是一个强大而灵活的三维空间定位工具,它可以通过平移、旋转和其它复杂的三维空间变换精确定位任何一个三维物体。
单击工具栏上的按钮打开三维球,使三维球附着在三维物体之上,从而方便地对它们进行移动和相对定位。
图示:三维球位置1.三维球的结构默认状态下三维球的形状如图示。
图示:三维球结构图三维球有一个中心点,一个平移轴和一个旋转轴。
①中心点:主要用来进行点到点的移动。
使用的方法是右击鼠标,然后从弹出的菜单中挑选一个选项。
②平移轴:主要有两种用法:一是拖动轴,使轴线对准另一个位置进行平移;二是右击鼠标,然后从弹出的菜单中选择一个项目进行定向。
③旋转轴:主要有两种用法:一是选中轴后,可以围绕一条从视点延伸到三维球中心的虚拟轴线旋转。
二是右击鼠标,然后从弹出的菜单中选择一个项目进行定向。
2.激活三维球使用三维球时,必须先选中三维模型,将三维球激活。
默认的三维球图标是灰色的,激活后显示为黄色。
三维球的激活状态:3.三维球颜色三维球有三种颜色:默认颜色(XYZ三个轴对应的颜色分别是红绿蓝)、白色和黄色。
①默认颜色:三维球与物体关联。
三维球动,物体会跟着三维球一起动。
②白色:三维球与物体互不关联。
三维球动,物体不动。
③黄色:表示该轴已被固定(约束),三维物体只能在该轴的方向上进行定位。
三维球与附着元素的关联关系,通过键盘空格键来转换。
三维球为默认颜色时按下空格键,则三维球会变白。
变白后,移动三维球时附着元素不动。
4.三维球的平移和旋转⏹平移:将零件,图素在指定的轴线方向上移动一定的距离,可在空白数值框内输入平移的距离,单位为mm。
图示:三维球的平移⏹旋转:将零件,图素在指定的角度范围内旋转一定的角度。
图示:三维球的旋转5.中心点的定位方法三维球的中心点,可进行点定位。
如图所示为三维球中心点的右键菜单。
图示:三维球中心点右键菜单(1)编辑位置:选择此选项可弹出位置输入框,用来输入相对父节点锚点的X、Y、Z三个方向的坐标值。
坐标变换和坐标系的旋转一、介绍在数学和计算机科学领域,坐标变换和坐标系的旋转是非常重要的概念。
它们可以帮助我们在多维空间中进行位置和方向的变换,以及解决各种几何问题。
本文将深入讨论坐标变换和坐标系的旋转原理、应用和方法。
二、坐标变换的概念1. 坐标系坐标系是用来描述多维空间中点的位置的一组规则。
常见的坐标系有笛卡尔坐标系、极坐标系和球坐标系等。
不同的坐标系拥有不同的表示方式和转换方式,可以根据实际需求进行选择和应用。
2. 坐标变换坐标变换是指将一个坐标系中的点的坐标转换到另一个坐标系中的过程。
在三维空间中,常见的坐标变换包括平移、缩放和旋转。
通过坐标变换,我们可以在不同的坐标系中对点进行描述和分析。
三、坐标系的旋转1. 二维空间的旋转在二维空间中,我们可以通过旋转矩阵来实现坐标系的旋转变换。
旋转矩阵是一个二维方阵,可以将二维平面上的点绕原点进行旋转。
旋转矩阵的组成元素由余弦和正弦函数值得到,具体的计算公式可由三角函数知识导出。
2. 三维空间的旋转在三维空间中,坐标系的旋转变换可以由旋转矩阵或四元数来实现。
旋转矩阵是一个3x3的正交矩阵,可以表示绕任意轴进行旋转的变换。
而四元数是一种特殊的数学工具,可以方便地进行复杂的旋转变换。
四、坐标变换和坐标系旋转的应用1. 图形学在计算机图形学中,坐标变换和坐标系旋转被广泛应用于三维建模、形体变换和动画制作等领域。
通过使用合适的坐标转换和旋转方法,我们可以在电脑屏幕上展示出逼真的三维图像和动画效果。
2. 机器人技术在机器人技术中,坐标变换和坐标系旋转被用于描述机器人的运动和姿态。
通过坐标变换和旋转操作,机器人可以精准地定位和移动,实现各种复杂的自动化任务。
3. 导航系统在导航系统中,通过坐标变换和坐标系旋转,我们可以将地球表面上的经纬度坐标转换为二维平面上的笛卡尔坐标系,从而实现地图的显示和位置定位。
五、总结坐标变换和坐标系旋转是数学和计算机科学中的重要概念,它们可以帮助我们在多维空间中进行位置和方向的变换,解决各种几何问题。
三维旋转坐标系变换旋转三维向量图中为单位向量,表⽰转轴。
将绕逆时针旋转⾓度得到。
可将分解为沿转轴的分量有其中为反对称矩阵。
那么式可写成:因此旋转作⽤可⽤⼀个矩阵表⽰。
旋转群旋转是线性变换,将变为1. 向量长度2.3. 相对⽅向1和2是等价的。
1推22推1因此可定义旋转群:旋转矩阵算符是线性的,可⽤矩阵表⽰,可得:即旋转矩阵是正交矩阵。
由旋转性质3(Special Orthogonal group),其中的special欧拉定理是说存在向量,使得旋转前后不变:就是转轴⽅向。
证明:只要证明有为1的特征值即可。
指数映射得:那么有得到:如果为常数,上述⽅程:其中矩阵的指数按泰勒级数定义。
这称为指数映射:还可以定义"⼤写的"指数映射:如果绕转轴转了⾓度上式按泰勒展开后得:这就是Rodrigues旋转公式。
推导过程⽤到了根据这个式⼦,⼜可写成:这就是式。
由可得:即:⼜有因此其中,这个矩阵的每⼀列都平⾏于,只要对⾮0转180度效果是⼀样四元数旋转公式为:旋转要求是单位四元数:还可以看到,⾃动保持了相对⽅向:其中第2和第5个等号是因为:指数映射得:两边左乘,得到:如果为常数,上式解得如果绕转轴转了⾓度“⼤写的”指数映射:旋转作⽤将式代⼊式,推导可得式,这就验证了的正确性。
四元数到旋转矩阵的转换由可以得到:旋转合成假设旋转2作⽤于旋转1之后。
对于旋转矩阵,对于四元数,因此,后旋转的都是乘在左边。
坐标系变换⽅向余弦矩阵(DCM)⽤G表⽰global,或者n系;L表⽰local,或者b系。
分别为向量在坐标系得:表⽰从到的坐标变换。
由对于⼀个与系固连的向量,经过主动旋转,得到⽽按定义:因此坐标变换矩阵与主动旋转矩阵欧拉⾓intrinsic rotation是指绕当前坐标系(⽽不是某个固定坐标系)的轴转动。
绕某轴逆时针旋转,得到。
对于绕轴旋转绕绕轴旋转,可得欧拉⾓和DCM的转换关系:若是⼩⾓度转动,各轴转过的⾓度有关。
三维坐标系旋转变换公式三维坐标系旋转变换公式是在几何中常用的一种数学变换,它既可以描述平面的旋转,又可以根据旋转角度和旋转轴,表达把物体从一个坐标系移动到另一个坐标系的变换。
本文重点介绍三维坐标系旋转变换公式的含义及其计算方法,并结合实例对其应用进行讨论。
一、三维坐标系旋转变换公式的含义三维坐标系,也称空间坐标系,是指三个坐标轴构成的坐标系,包括X轴、Y轴和Z轴,直观上它仿佛是一个立方体,其中每个方向上的坐标变化都可以依据三维坐标系旋转变换公式表达出来。
三维坐标系旋转变换公式定义为:$$x =cos(θ)x-sin(θ)y$$$$y=sin(θ)x+cos(θ)y$$$$z =z,$$其中θ表示坐标系旋转变换时所采用的旋转角度,x和y表示原坐标系中的坐标,x和y表示变换后的坐标。
二、三维坐标系旋转变换公式的计算在三维坐标系中,当给定旋转角度和旋转轴时,可以根据三维坐标系旋转变换公式计算坐标变换。
旋转轴的方向可以用单位向量描述,单位向量的方向是指该向量在原点指向的方向,以及该向量的大小。
计算坐标变换时,首先需要计算旋转矩阵,旋转矩阵定义为:$$R=begin{bmatrix}cos(θ) & sin(θ) & 0-sin(θ) & cos(θ) & 00 & 0 & 1end{bmatrix}$$旋转矩阵可以表示坐标系旋转时的线性变换,在坐标变换时,可以将坐标矩阵与旋转矩阵进行乘积运算,即可得到变换后的坐标。
三、三维坐标系旋转变换实例假设存在一个三维坐标系,其中的坐标为(1,2,3),且坐标系旋转角度为90度,旋转轴方向为(1,0,0),则可以用三维坐标系旋转变换公式计算变换后的坐标。
首先,计算旋转矩阵,根据旋转变换公式可知,当θ=90°时,旋转矩阵为:$$R=begin{bmatrix}0 & 1 & 0-1 & 0 & 00 & 0 & 1end{bmatrix}$$然后,将待变换的坐标(1,2,3)与旋转矩阵进行乘积,可以得到变换后的坐标(2,-1,3)。
球坐标系与直角坐标系的转换关系球坐标是一种三维坐标。
分别有原点、方位角、仰角、距离构成。
设P (x, v, z)为空间内一点,那么点P也可用这样三个有次序的数r, 4,。
来确定,其中r为原点。
与点P间的距离,0为有向线段与z轴正向所夹的角,力为从正z轴来看自x轴按逆时针方向转到有向线段的角,这里M为点P在xOy面上的投影。
这样的三个数r, ()),0叫做点P的球面坐标,这里r,力,。
的变化范围为区[0,+ 8 ),4 c[0, 2 兀],M [0,兀].当r,。
或力分别为常数时,可以表示如下特殊曲面:r =常数,即以原点为心的球面;0 =常数,即以原点为顶点、z轴为轴的圆锥面;4 =常数,即过z轴的半平面。
与直角坐标系的转换:1).球坐标系(r, 0 ,4 )与直角坐标系(x,v,z)的转换关系:x=rsin 0 cos(j)y=rsin 0 sin())z=rcos 02).反之,直角坐标系(x,y,z)与球坐标系(r,。
,力)的转换关系为:r= sqrt(x*2 + y*2 + z*2);())=arctan(y/x);0 = arccos(z/r);球坐标系下的微分关系:在球坐标系中,沿基矢方向的三个线段元为:dl(r)=dr, dl( 0 )=rd 0 , dl( 4 )=rsin 0 d())球坐标的面元面积是:dS=dl( 0 )* dl(()))=r A2*sin 0 d 0 d(f)体积元的体积为:dV=dl(r)*dl( 0 )*dl( 4 )=rA2*sin 0 drd 0 d 4球坐标系在地理学、天文学中有着广泛应用.在测量实践中,球坐标中的。
角称为被测点P (r, 0 , 4 )的方位角,90° — 0成为上下角。
生成旋转矩阵的一种简单方式是把它作为三个根本旋转的序列复合。
关于右手笛卡尔坐标系的x-, y-和z-轴的旋转分别叫做 roll, pitch 和yaw 旋转。
球坐标系和旋转坐标系球坐标系和旋转坐标系是物理学和数学中常用的两种坐标系,它们分别在描述三维空间中的点和旋转运动时起到了重要的作用。
本文将分别介绍球坐标系和旋转坐标系的定义、转换和应用,并对其优缺点进行探讨。
一、球坐标系1. 定义球坐标系是一种描述三维空间中点的坐标系,通过半径、极角和方位角来确定一个点的位置。
其中,半径表示点到原点的距离,极角表示点与正半轴的夹角,方位角表示点在极角确定的平面上与正半轴的夹角。
2. 转换公式在球坐标系中,点的坐标表示为(r, θ, φ),其中r为半径,θ为极角,φ为方位角。
与直角坐标系的转换关系如下:x = r * sinθ * cosφy = r * sinθ * sinφz = r * cosθ3. 应用球坐标系常用于描述以原点为中心的球体或球面上的物理问题,如天文学中的行星运动、地理学中的地球表面、分子结构中的电子云等。
由于球坐标系在球对称问题上有优势,因此在物理领域具有广泛的应用。
二、旋转坐标系1. 定义旋转坐标系是一种描述物体绕固定轴旋转时的坐标系,通过主轴角和欧拉角来确定物体的方向。
其中,主轴角表示物体绕固定轴旋转的角度,欧拉角包括姿态角、俯仰角和滚转角,用于细致描述物体在三个正交轴上的旋转情况。
2. 转换公式在旋转坐标系中,点的坐标表示为(α, β, γ),其中α为主轴角,β、γ为欧拉角。
与直角坐标系的转换关系如下:x = cosα * cosβ * cosγ - sinα * sinγy = sinα * cosβ * cosγ + cosα * sinγz = sinβ * cosγ3. 应用旋转坐标系广泛应用于刚体动力学、空间机器人、航天器姿态控制等领域。
通过旋转坐标系的描述,可以更准确地分析和控制物体的旋转状态,以满足不同工程和科学问题的需求。
三、球坐标系与旋转坐标系的联系球坐标系和旋转坐标系在描述三维空间中的点和旋转运动时具有不同的应用领域。
球坐标系求旋度简介球坐标系是一种常见的三维坐标系,用于描述空间中的点的位置。
在物理学和工程领域中,球坐标系经常用于描述具有球对称性的问题,例如流体力学和电磁学中的旋度。
旋度是一个向量运算,描述了矢量场的旋转性质。
在球坐标系中,求解旋度需要一些特殊的计算方法。
球坐标系简介球坐标系由径向距离 r、极角θ 和方位角φ 组成。
径向距离 r 表示点到坐标原点的距离,极角θ 表示点与正 z 轴的夹角,方位角φ 表示点在 xy 平面上的投影与正 x 轴的夹角。
球坐标系中,坐标原点对应 (0, 0, 0)。
球坐标系与直角坐标系之间的转换关系如下:•x = r * sin(θ) * cos(φ)•y = r * sin(θ) * sin(φ)•z = r * cos(θ)旋度的定义旋度是一个向量运算,它描述了矢量场的旋转性质。
如果一个矢量场的旋度为零,则该场是无旋场,表示该矢量场在每一点上都没有旋转。
旋度的计算可以用矢量微分算子来表示:•旋度 = ∇ × V其中,∇表示梯度算子,× 表示叉乘运算,V 表示矢量场。
球坐标系中的旋度计算在球坐标系中,旋度的计算需要使用一些特殊的技巧。
根据矢量微分运算规则,在球坐标系下,旋度的公式可表示为:•∇ × V = (1 / (r * sin(θ))) * [(∂(Vz * sin(θ)) / ∂θ) - ∂(Vy * cos(θ)) / ∂φ] * er + (1 / r) * [(1 / sin(θ)) * (∂(Vr * sin(θ)) / ∂φ) - ∂Vφ / ∂r] * eθ + (1 / r) * (1 / sin(θ)) * [∂(Vr * sin(θ)) / ∂θ - ∂Vθ / ∂r] * eφ其中,∂ 表示偏导数,er、eθ、eφ 分别表示径向、极角和方位角方向上的单位向量。
Vr、Vθ、Vφ 分别表示矢量场在径向、极角和方位角方向上的分量。
球坐标系与直角坐标系的转换关系
球坐标是一种三维坐标。
分别有原点、方位角、仰角、距离构成。
设P(x,y,z)为空间内一点,则点P也可用这样三个有次序的数r,φ,θ来确定,其中r为原点O与点P间的距离,θ为有向线段与z轴正向所夹的角,φ为从正z轴来看自x轴按逆时针方向转到有向线段的角,这里M为点P在xOy面上的投影。
这样的三个数r,φ,θ叫做点P的球面坐标,这里r,φ,θ的变化范围为
r∈[0,+∞),
φ∈[0, 2π],
θ∈[0, π] .
当r,θ或φ分别为常数时,可以表示如下特殊曲面:
r = 常数,即以原点为心的球面;
θ= 常数,即以原点为顶点、z轴为轴的圆锥面;
φ= 常数,即过z轴的半平面。
与直角坐标系的转换:
1).球坐标系(r,θ,φ)与直角坐标系(x,y,z)的转换关系:
x=rsinθcosφ
y=rsinθsinφ
z=rcosθ
2).反之,直角坐标系(x,y,z)与球坐标系(r,θ,φ)的转换关系为:
r= sqrt(x*2 + y*2 + z*2);
φ= arctan(y/x);
θ= arccos(z/r);
球坐标系下的微分关系:
在球坐标系中,沿基矢方向的三个线段元为:
dl(r)=dr, dl(θ)=rdθ, dl(φ)=rsinθdφ
球坐标的面元面积是:
dS=dl(θ)* dl(φ)=r^2*sinθdθdφ
体积元的体积为:
dV=dl(r)*dl(θ)*dl(φ)=r^2*sinθdrdθdφ
球坐标系在地理学、天文学中有着广泛应用.在测量实践中,球坐标中的θ角称为被测点P(r,θ,φ)的方位角,90°-θ成为高低角。
生成旋转矩阵的一种简单方式是把它作为三个基本旋转的序列复合。
关于右手笛卡尔坐标系
的x-, y- 和z-轴的旋转分别叫做roll, pitch 和yaw 旋转。
因为这些旋转被表达为关于一个轴的旋转,它们的生成元很容易表达。
绕x-轴的旋转定义为: 这里的θx 是roll 角。
绕y-轴的旋转定义为: 这里的θy 是pitch 角。
绕z-轴的旋转定义为: 这里的θz 是yaw 角。
三维空间中的旋转变换比二维空间中的旋转变换复杂。
除了需要指定旋转角外,还需指定旋转轴。
若以坐标系的三个坐标轴x,y,z分别作为旋转轴,则点实际上只在垂直坐标轴的平面上作二维旋转。
此时用二维旋转公式就可以直接推出三维旋转变换矩阵。
规定在右手坐标系中,物体旋转的正方向是右手螺旋方向,即从该轴正半轴向原。