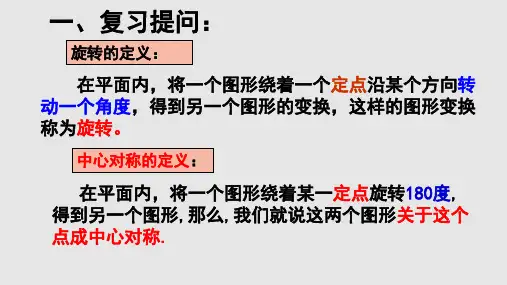
4坐标系中的旋转变换(2011年)

1. (2016 广西河池市) 】．如图，在平面直角坐标系中，O 为坐标原点，点A 的坐标为（1,3）．将线段OA 绕原点O 逆时针旋转30°，得到线段OB ，则点B 的坐标是（ ）A ．(0,2)B ．(2,0)C ．（1,―3）D ．（―1,3）答案：】．答案A逐步提示作AC ⊥x 轴于点C ，根据勾股定理求出OA 的长，根据正切的概念求出∠AOC 的度数，再根据旋转变换即可得解.详细解答解：过点A 作AC ⊥x 轴于点C .∵点A 的坐标为（1,3），∴OC ＝1，AC ＝3．∴OA ＝12＋ (3)2＝2.∵tan ∠AOC ＝AC OC＝3,∴∠AOC ＝60°.∴将线段OA 绕原点O 逆时针旋转30°得到线段OB 时，点B 恰好在y 轴上.∴点B 的坐标是(0,2) .故选择A.解后反思本题通过作垂线，将点的坐标转化为线段的长度，应用勾股定理求斜边的长，应用特殊角的三角函数值求出特殊角的度数，再根据旋转的方向和角度确定所求点的位置，最后写出其坐标.关键词 图形旋转的特征、特殊角三角函数值的运用、点的坐标20160926210454015732 4 坐标系中的旋转变换 选择题 基础知识 2016/9/262. (2016 广西贺州市) 】．如图，将线段AB 绕点O 顺时针旋转90°得到线段A ′B ′，那么A （﹣2，5）的对应点A ′的坐标是（ ）A．（2，5） B．（5，2） C．（2，﹣5） D．（5，﹣2）答案：】．考点坐标与图形变化-旋转．分析由线段AB绕点O顺时针旋转90°得到线段A′B′可以得出△ABO≌△A′B′O′，∠AOA′=90°，作AC⊥y轴于C，A′C′⊥x轴于C′，就可以得出△ACO≌△A′C′O，就可以得出AC=A′C′，CO=C′O，由A的坐标就可以求出结论．解答解：∵线段AB绕点O顺时针旋转90°得到线段A′B′，∴△ABO≌△A′B′O′，∠AOA′=90°，∴AO=A′O．作AC⊥y轴于C，A′C′⊥x轴于C′，∴∠ACO=∠A′C′O=90°．∵∠COC′=90°，∴∠AOA′﹣∠COA′=∠COC′﹣∠COA′，∴∠AOC=∠A′OC′．在△ACO和△A′C′O中，，∴△ACO≌△A′C′O（AAS），∴AC=A′C′，CO=C′O．∵A（﹣2，5），∴AC=2，CO=5，∴A′C′=2，OC′=5，∴A′（5，2）．故选：B．点评本题考查了旋转的性质的运用，全等三角形的判定及性质的运用，等式的性质的运用，点的坐标的运用，解答时证明三角形全等是关键。

苏教版选修4《极坐标系中的旋转变换》说课稿引言《极坐标系中的旋转变换》是苏教版选修4中的一篇数学课文，本篇课文通过介绍极坐标系中的旋转变换，旨在帮助学生理解极坐标系的概念及其在几何图形中的应用。

通过本课文的学习，学生将能够掌握极坐标系中的旋转变换的基本概念、方法和相关运算，并能够运用所学知识解决实际问题。

一、学情分析本节课内容适用于高中数学选修课程，学生已经掌握了直角坐标系和极坐标系的基本概念及其转换关系。

对于旋转变换这一概念，学生可能有一些模糊的认识，但他们已经学习了平面向量相关内容，对于向量的旋转有一定的了解。

因此，本课将通过对比向量的旋转和极坐标系中的旋转变换，帮助学生更深入地理解极坐标系中的旋转变换。

二、教学目标通过本节课的学习，学生将能够： 1. 理解极坐标系中的旋转变换的概念； 2. 掌握极坐标系中的旋转变换的基本方法；3. 能够运用极坐标系中的旋转变换解决几何问题；4. 培养学生的逻辑思维和几何推理能力。

三、教学重点与难点1. 教学重点•极坐标系中的旋转变换的概念和基本方法；•运用极坐标系中的旋转变换解决几何问题。

2. 教学难点•极坐标系中的旋转变换与向量的旋转的比较；•运用极坐标系中的旋转变换解决复杂的几何问题。

四、教学过程步骤一：导入与引入（5分钟）1.引导学生回顾直角坐标系与极坐标系的基本概念及其转换关系；2.提问：在直角坐标系中，我们学过向量的旋转，那在极坐标系中是否也存在旋转变换？3.引入本节课的话题：我们今天要学习的是《极坐标系中的旋转变换》。

步骤二：学习与讲解（20分钟）1.讲解极坐标系中的旋转变换的概念与基本方法：–给出旋转变换的定义：极坐标系中，以原点为中心，逆时针旋转一个角度θ，得到的新坐标称为旋转变换；–引导学生进行基本的旋转变换操作，帮助理解旋转变换的方法和过程；–通过实例演示，让学生掌握极坐标系中的旋转变换的基本运算规则。

2.比较向量的旋转和极坐标系中的旋转变换：–将直角坐标系中的向量旋转和极坐标系中的旋转变换进行对比，帮助学生更好地理解两者之间的关系和差异。

旋转四元数坐标系变换引言：在三维空间中，我们经常需要进行坐标系的变换，以便描述物体在不同坐标系下的位置和姿态。

旋转四元数是一种常用的表示旋转的数学工具，它能够简洁、高效地描述三维空间中的旋转变换。

本文将介绍旋转四元数的基本原理和应用，以及如何利用旋转四元数进行坐标系的变换。

一、旋转四元数的定义与性质1.1 定义旋转四元数是一种四维复数，通常表示为q = a + bi + cj + dk，其中a、b、c、d均为实数，i、j、k为虚数单位。

旋转四元数具有四个分量，分别对应于一个三维旋转的轴和角度。

其中，a为实部，表示旋转角度的余弦值；b、c、d为虚部，表示旋转轴的三个分量。

1.2 性质旋转四元数具有以下性质：（1）单位化：旋转四元数的模长为1，即|q| = 1。

这是为了保证旋转四元数的归一性，使其能够准确表示旋转变换。

（2）共轭：旋转四元数的共轭定义为q* = a - bi - cj - dk，即虚部取相反数。

共轭用于表示旋转的逆变换。

（3）乘法：旋转四元数的乘法是非交换的，即q1q2 ≠ q2q1。

旋转四元数的乘法可以用于将两个旋转变换合成为一个旋转变换。

（4）逆元：旋转四元数的逆元定义为q-1 = q*/|q|2，即共轭除以模长的平方。

逆元用于表示旋转的逆变换。

二、旋转四元数的应用2.1 旋转变换旋转四元数可以用于表示三维空间中的旋转变换。

对于一个给定的旋转四元数q，可以通过与向量v的乘法操作，实现将向量v绕旋转轴q的旋转。

2.2 坐标系变换利用旋转四元数，我们可以方便地进行坐标系的变换。

假设有两个坐标系A和B，坐标系A与坐标系B之间存在一个旋转变换，我们可以通过旋转四元数来描述这个变换。

具体步骤如下：（1）定义旋转四元数q，表示坐标系A到坐标系B的旋转变换。

（2）将坐标系A的原点Oa表示为旋转四元数的形式，即Oa = 0 + i0 + j0 + k0。

（3）将坐标系A的一个单位向量Va表示为旋转四元数的形式，即Va = 0 + i1 + j0 + k0。

坐标系中的变换
坐标系中的变换是指在二维或三维坐标系中，通过某些操作将原始坐标系中的点映射到新的坐标系中的点的过程。

常见的坐标系变换包括平移、旋转、缩放、镜像等操作。

其中平移是指将所有点都沿着某个方向移动一定的距离，旋转是指将所有点绕着某个点旋转一定的角度，缩放是指将所有点沿着某个方向缩放一定的比例，镜像是指将所有点沿着某个轴对称。

坐标系变换在计算机图形学中有着广泛的应用，如图像的旋转、缩放、平移等操作都是通过坐标系变换实现的。

在数学中，坐标系变换也是一个重要的概念，它被广泛应用于线性代数、微积分等领域。

需要注意的是，坐标系变换不仅可以应用于二维或三维坐标系，也可以应用于更高维度的坐标系。

此外，坐标系变换还可以通过矩阵运算来实现，这种方法更为高效和灵活。

- 1 -。

《23.1.2旋转作图与坐标系中的旋转变换》一、学习目标1.能按要求作出简单平面图形旋转后的图形.2.能通过图形的旋转设计图案.二、导学指导与检测导学导学检测及课堂展示阅读教材第60页例题完成右边的学习内容1.教材第60页例题自学参考提纲：①因为A是旋转中心，所以A点的对应点是.②根据正方形的性质：AD＝AB，∠OAB＝90°，所以点D的对应点是.③因为旋转前、后的两个图形全等，所以本例根据三角形全等的判定方法.作出△ADE的对应图形为..④E点的对应点E′，还有别的方法作出来吗？（1）作一个图形旋转后的图形，关键是作出对应点，并按原图的顺序依次连接各对应点.（2）在△ABC中，AB＝AC，P是BC边上任意一点，以点A为中心，取旋转角等于∠BAC，把△ABP 逆时针旋转，画出旋转后的图形.三．巩固诊断一、基础巩固（70分）1.(10分) 将△AOB绕点O旋转180°得到△DOE，则下列作图正确的是（）A B C D2.(10分) 数学课上，老师让同学们观察如图所示的图形，问：它绕着圆心O旋转多少度后和它自身重合？甲同学说：45°；乙同学说：60°；丙同学说：90°；丁同学说：135°．以上四位同学的回答中，错误的是（）A．甲B．乙C．丙D．丁3.(10分) 如图，将一个钝角△ABC（其中∠ABC=120°）绕点B顺时针旋转得到△A1BC1，使得C点落在AB的延长线上的点C1处，连接AA1．（1）写出旋转角的度数；（2）求证：∠A1AC=∠C1．4.(20分) 分别画出△ABC 绕点O 逆时针旋转90°和180°后的图形.5.(20分)把图中的△ABC 作下列旋转:（1）以C 为中心，把这个三角形顺时针旋转60°；（2）在△ABC 外任取一点O 为中心，把这个三角形顺时针旋转120°.二、综合应用（20分）6.(10分)如图，在Rt △ABC 中，∠ACB=90°，∠A=40°，以直角顶点C 为旋转中心，将△ABC 旋转到△A′B′C 的位置，其中A′、B′分别是A 、B 的对应点，且点B 在斜边A′B′上，直角边CA′交AB 于点D ，则旋转角等于（ ）A.70°B.80°C.60°D.50°7.(10分)右图中的风车图案，可以由哪个基本的图形，经过什么样的旋转得到？ABCC三、拓展延伸（10分）8.(10分) 如图，△ABC中，∠C=90°，∠B=40°，点D在边BC上，BD=2CD．△ABC绕着点D顺时针旋转一定角度后，点B恰好落在初始△ABC的边上，求旋转角α（0°＜α＜180°）的度数.四、堂清、日清记录堂清日清今日之事今日毕日积月累成大器课堂反思：。

坐标旋转公式是一种重要的数学公式，它可以用来描述物体在空间坐标系内的旋转运动。

它可以帮助我们准确地表达空间中物体的旋转情况，并且可以用来计算物体的空间坐标位置。

坐标旋转公式的基本原理是，以原点为中心，以某条轴为轴心，沿着该轴旋转一定的
角度，然后将原来的坐标系的三个坐标轴向量旋转一定的角度，就可以表示物体在旋转后
坐标系下的新坐标位置。

坐标旋转公式的基本形式是三维旋转矩阵R，它表示一个由三个坐标轴组成的坐标系，经过旋转后，变换成另外一个坐标系，它的表达形式是：
R=cosθ -sinθ 0
sinθ cosθ 0
0 0 1
其中，θ表示旋转角度，R表示旋转矩阵，经过旋转后，三个坐标轴的坐标位置就发
生了变化。

坐标旋转公式是空间几何的基本概念，它可以用来表达物体在空间上的旋转运动，及
求解物体在空间中的坐标位置。

它的应用非常广泛，可以应用在机器人控制、空间探测、
机械设计等领域中。

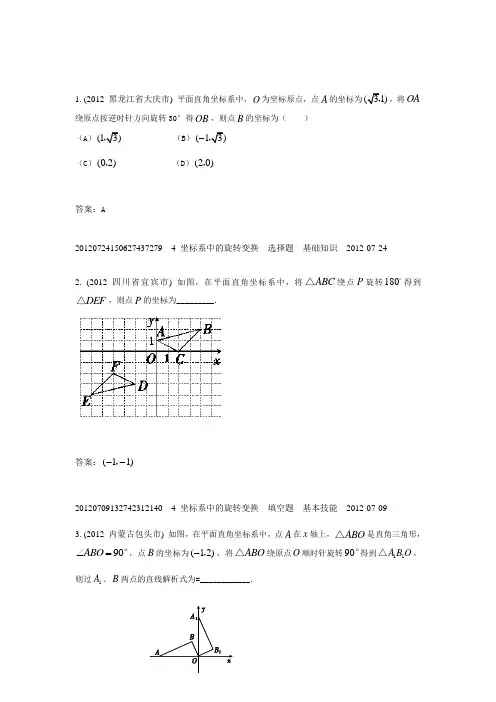
1. (2012 黑龙江省大庆市) 平面直角坐标系中，O 为坐标原点，点A 的坐标为(31)，，将OA 绕原点按逆时针方向旋转30°得OB ，则点B 的坐标为（ ）（A ）(13)， （B ）(13)-， （C ）(02)， （D ）(20)，答案：A20120724150627437279 4 坐标系中的旋转变换 选择题 基础知识 2012-07-242. (2012 四川省宜宾市) 如图，在平面直角坐标系中，将ABC △绕点P 旋转180得到DEF △，则点P 的坐标为_________．答案：(11)--，20120709132742312140 4 坐标系中的旋转变换 填空题 基本技能 2012-07-093. (2012 内蒙古包头市) 如图，在平面直角坐标系中，点A 在x 轴上，ABO △是直角三角形，90ABO ∠=°，点B 的坐标为(12)-，，将ABO △绕原点O 顺时针旋转90°得到11A B O △，则过1A 、B 两点的直线解析式为=____________．答案：35y x =+20120706100651671109 4 坐标系中的旋转变换 填空题 数学思考 2012-07-064. (2012 山东省泰安市) 如图，菱形OABC 的顶点O 在坐标原点，顶点A 在x 轴上，120B ∠=°，2OA =，将菱形OABC 绕原点O 顺时针旋转105°至OA B C ′′′的位置，则点B ′的坐标为（ ）．（A ）22， （B ）(22-， （C ）()22-， （D ）33，答案：A20120704171839921561 4 坐标系中的旋转变换 选择题 数学思考 2012-07-04。

坐标旋转变换空间直角坐标系如果其原点不动，绕着某一个轴旋转而构成的新的坐标系，这个过程就叫做坐标旋转。

在旧坐标系中的坐标与在旋转后新坐标系中的坐标有一定的转换关系，这种转换关系可以用转换矩阵来表示。

如图1，直角坐标系XYZ ，P 点的坐标为),,(z y x ，其相应的在XY 平面，XZ 平面，YZ 平面分别为)0,,(y x M ，),0,(z x Q 和),,0(z y N 。

),,(z y x P Oxyz)0,,(y x M ),,0(z y N ),0,(z x Q图1直角坐标系XYZ设ϑ表示第j 轴的旋转角度，()R j ϑ表示绕第j 轴的旋转，其正方向是沿坐标轴向原点看去的逆时针方向。

很明显当j 轴为旋转轴时，它对应的坐标中的j 分量是不变的。

由于直角坐标系是对称的，下面我们以绕z 轴旋转为例推导其旋转变换矩阵，其它两个轴推导和它是一样的。

设图1的坐标绕Z 轴逆时针旋转θ角度，新坐标为'''Z Y X ，如图2所示：)',','z y x XY)0,',y ,0(N )',0,'(|)z x 'Y图2 坐标绕Z 轴逆时针旋转θ角度由于坐标中的z 分量不变，我们可以简化地在XY 平面进行分分析，如图3所示：X Y'X 'Y θθ)0,','( |)0,,(y x y x M 'X M XM ϕO图3 坐标绕Z 轴逆时针旋转θ角度的XY 平面示意图点X M 和点'X M 分别是M 点在X 轴和'X 轴的投影。

如图3⎩⎨⎧−=∠==−=∠==)sin(sin )cos(cos θϕθϕOM MOM OM MM y OM MOM OM OM x X X X X (1) ⎩⎨⎧=∠===∠==ϕϕsin sin cos cos '''''OM MOM OM MM y OM MOM OM OM x X X X X (2) 把(1)式按照三角函数展开得：⎩⎨⎧−=+=θϕθϕθϕθϕsin cos cos sin sin sin cos cos OM OM y OM OM x (3) 把(2)式代入(3)式得：⎩⎨+−=θθcos 'sin 'y x y (4) 坐标中的z 分量不变，即'z z =这样整个三维坐标变换就可以写成（用新坐标表示就坐标）：⎪⎩⎪⎨⎧=+−=+='cos 'sin 'sin 'cos 'z z y x y y x x θθθθ (5) 把式(5)用一个坐标旋转变换矩阵()θR Z 表示可以写成：()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡'''z y x z y x Z θR (6)()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡−=1 0 0 0 cos sin 0 sin cos θθθθθR Z (7) 坐标系'''Z Y X 是坐标系XYZ 绕Z 轴逆时针旋转θ角度而来，从另一个角度来看，也可以说坐标系XYZ 是坐标系'''Z Y X 绕'Z 轴逆时针旋转θ−角度而来，所以根据(6)式有（上标"1"−表示矩阵的逆）：()()()θR θR θR −=⇒⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡−=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡−Z Z Z z y x z y x 1''' (8)用同样的分析办法，当绕X 轴逆时针旋转θ角度其YZ 平面分析如图4所示：Y Z'Y 'Z θθ)',0,'(|),0,(z x z x N 'Y N YN ϕO图4 坐标绕X 轴逆时针旋转θ角度的YZ 平面示意图其坐标转换关系为：⎪⎩⎪⎨=+−='cos 'sin 'x x z y z θθ (9) ()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡−=θθθcos sin 0sin cos 00 0 1θX θR (10) ()()θR θR −=−X X 1 (11)当绕Y 轴逆时针旋转θ角度得其XZ 平面分析如图5所示（注意和前面两个角度方向不一样）：XZ'X 'Z θθ)',',0( |),,0(z y z y Q 'X Q XQ ϕO图5 坐标绕Y 轴逆时针旋转θ角度的XZ 平面示意图⎪⎩⎪⎨⎧=+=−='cos 'sin 'sin 'cos 'y y z x z z x x θθθθ (12) ()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡−=θθθcos 0 sin 0 1 0sin 0 cos θY θR (13) ()()θR θR −=−Y Y1(14)。