基于Benford法则的舞弊检测方法研究

利用奔福德定律开展财务造假案例研究发布时间：2021-05-19T03:18:37.761Z 来源：《中国科技人才》2021年第8期作者：岳娇[导读] 1881年，美国数学家、天文学家西蒙·纽卡姆（SimonNewcomb）无意间发现自然数中许多类型的数字都能很好的遵从这个规律，即：数字1出现在首位的概率明显大于2出现在首位的概率，数字2出现在首位的概率又大于3出现在首位的概率，其他数字以此类推能够得到相同结论。

浙江能源天然气集团有限公司 310051摘要: 财务造假一直以来都是一个顽疾，并且长期困扰审计学界。

奔福德定律是一个数学定律，揭示了不同数位上数字的分布概率，在会计、审计领域中引入奔福德定律，能够起到传统审计技术意想不到的效果。

利用奔福德定律开展财务造假案例研究，能够有效的提升审计技术，为高效预测财务造假行为提供了全新的思路。

关键词：奔福德定律预测舞弊案例研究一、奔福德定律的简介1881年，美国数学家、天文学家西蒙·纽卡姆（SimonNewcomb）无意间发现自然数中许多类型的数字都能很好的遵从这个规律，即：数字1出现在首位的概率明显大于2出现在首位的概率，数字2出现在首位的概率又大于3出现在首位的概率，其他数字以此类推能够得到相同结论。

但这一数学现象却在50多年的时间里都没有受到应有的重视，直到1938年才重新受到数学界的关注。

1938年，美国通用电气的物理学家弗兰克·奔福德（FrankBenford）他观察到了同样的现象。

他收集并验证了20组共20229个不同类型的数据，这些数据中包括：原子辐射的半衰期、原子的摩尔重量、物理与数学常数、河流的流域面积、城镇人口分布数、电费账单等，从实证的角度验证了西蒙·纽卡姆的理论，即：数字1在首位出现的概率约为30%，数字2在首位出现的概率约为17%，数字3在首位出现的概率约为12%，而8和9在首位出现的概率约为5%和4%。

论奔福德定律在舞弊审计中的应用作者：魏茜嘉来源：《现代经济信息》 2018年第18期引言安然事件的爆发为企业的健康发展敲响了警钟，企业财务信息的公开及真实性的验证受到各界的高度重视。

运用奔福德定律对安然公司2001 至2002 年间所公布的“每股盈利”数据进行检验后发现了较大的差异，后续的审计调查核实确实存在财务舞弊行为。

这一事件之后，众多学者对奔福德定律进行了研究，并将其运用于各行业的数据分析。

一、奔福德定律简介弗瑞克·奔福德曾就职于通用电气实验室，他在上世纪初探究出一系列神奇的数学法则，即在任何一组随机整数数据中，数字1出现的概率大于数字2 出现的概率，同样数字2 出现的概率大于数字3 出现的概率，以此类推后面的数据也呈现出相同的分布规律。

例如日常生活中随机生成的电话号码，其中数字1 出现的概率通常要大于数字9 出现的概率。

会计学教授马克·尼格里尼(Mark J.Nigrini) 于1996 年计算出0~9 在数字的第一位出现的概率表，随后利用奔福德定律识别出会计造假、欺诈和逃税行为。

由此奔福德定律逐渐在财务领域大展身手。

二、奔福德定律与舞弊审计的联系传统的分析性复核依据财务数据的内在关系或者逻辑联系对财务数据进行检验，奔福德定律则是从数值统计的角度揭示数据的内在规律。

真实数据与奔福德定律最为接近，而在人为数据造假操作中，为了使数据显得较为随机，人们通常会等概率地选择0-9 中的所有数字，从而打破奔福德定律。

从国外的研究论证和一系列实证案例来看，将奔福德定律运用于审计，尤其是舞弊审计，作为实质性分析程序的补充，能够取得较好的效果。

随着我国的信息化建设不断推进，信息技术的进步和硬件设施的完善为奔福德定律的应用铺平了道路。

三、银广夏案例分析2001 年银广夏的财务造假丑闻被媒体曝光。

其在1998~2001年间虚增利润77156.7 万元，而在这三年中公司实际上却一直是亏损状态。

利用本福特定律快速发现数据异常实践
今天向大家介绍一种可以快速判断数据异常的定律——本福特定律。

本福特定律是由美国数学家、天文学家西蒙·纽卡姆于1881年首次发现。

在使用对数表做计算时，纽卡姆突然注意到对数表的第一页要比其它页更为破旧。

经过大量的统计分析，他发现，以1为首位的随机数的出现概率要比以2为首位的随机数高，而以2为首位的随机数的出现概率又要比以3为首位的随机数高，以此类推。

但纽卡姆并未对此做出解释，当时的人们也未给予充分关注，这一发现逐渐被淡忘。

1938年，美国通用电器的物理学家法兰克·本福特注意到了同样的现象，并进行了大量的分析验证。

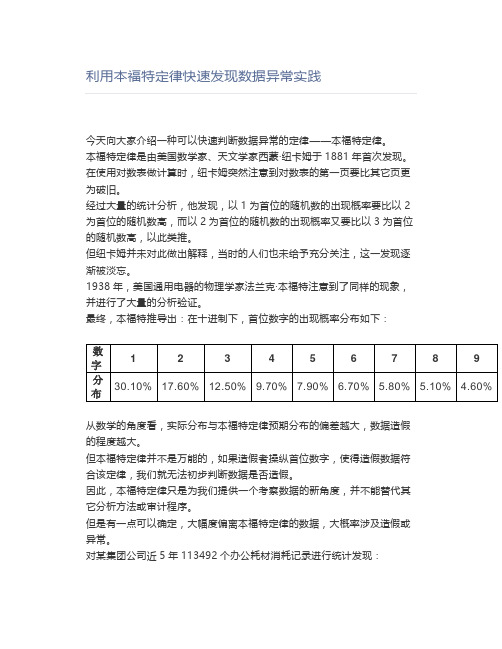
最终，本福特推导出：在十进制下，首位数字的出现概率分布如下：
从数学的角度看，实际分布与本福特定律预期分布的偏差越大，数据造假的程度越大。

但本福特定律并不是万能的，如果造假者操纵首位数字，使得造假数据符合该定律，我们就无法初步判断数据是否造假。

因此，本福特定律只是为我们提供一个考察数据的新角度，并不能替代其它分析方法或审计程序。

但是有一点可以确定，大幅度偏离本福特定律的数据，大概率涉及造假或异常。

对某集团公司近5年113492个办公耗材消耗记录进行统计发现：
能看出明显异常吗？
异常即为妖！审计人员带着怀疑对异常的数据5开头的数据进行分析发现：硒鼓与打印纸之间存在相关性。

按照单位对硒鼓与打印纸的数据进行对比发现下图异常的数据在红色方框之外。

沿着数据异常这个思路进一步分析发现了虚假冒用以物易物的现象，提出加强管理建议后效果显著。

2017年该方面的费用支出同比节约了近50%。

奔福德定律及其在审计中的应用研究最近几年来国内外显现了许多审计失败丑闻，其缘故固然很复杂，但现有审计技术和方式的局限性可能是其中最重要的因素之一。

因此，在经济业务日趋复杂多变，被审单位舞弊、讹诈手腕日趋隐蔽的背景下，完善现有舞弊审计的理论水平和技术方式变得尤其重要。

在过去20年里，国内外学术界和实务界就如何提高和改良审计师揭露财务舞弊的能力已开展了大量的研究，探讨了一些统计与数值分析技术和方式。

其中，奔福德定律(Benford's law)在侦查财务讹诈征兆方面具有必然的有效性。

奔福德定律揭露了在知足特定条件情形下大量统计数据中阿拉伯数字1～9在数据首位显现的概率散布规律。

笔者介绍了奔福德定律的理论内涵及其在审计中应用的理论和实践功效，并进一步探讨了在审计实践中应用奔福德定律的条件及应注意的问题。

一、奔福德定律的内涵(一)奔福德定律经典理论奔福德定律是由美国数学家、天文学家赛蒙·纽卡姆(Simon Newcomb)在1881年第一次发觉的。

通过对大量随机数据的统计分析，他发觉这些数据都专门好地符合如此的规律：以1为第一名数的随机数要比以2为第一名数的随机数显现的概率要大，而以2为第一名数的随机数要比以3为第一名数的随机数显现的概率要大，依此类推。

大约50年以后，美国通用电器的物理学家弗瑞克·奔福德(Frank Benford)又独立发觉了这一现象并得出了和Newcomb一样的结论。

他搜集了很多数据进行分析来验证自己的假说，这些数据包括了尽可能多的种类和范围，数据的搜集和整理花费了他7年的时刻。

他验证了总数为20229个的20组数字，其中包括篮球竞赛的数字、河流的长度、湖泊的面积、各城市人口散布数字、在某一杂志里显现的所有数字等。

弗瑞克·奔福德推导了奔福德定律的数学表达式，即数字的第一名上各个非0数字显现的概率，用公式(1)表达如下：其中：D：1，2，3……9；P=probability代表概率。

基于Benford法则的企业财务数据质量评价引言在当今高度数字化的商业环境中，财务数据质量是企业运营和管理的关键。

企业依赖精确、准确的财务数据来做出决策、向投资者和监管机构报告和展示其财务状况。

企业的财务数据可能受到错误、欺诈或不当处理的影响，这将直接影响到企业的绩效和声誉。

Benford法则是一种用于评估数字数据真实性和质量的方法，它可以用于评估企业的财务数据质量。

本文将介绍Benford法则，并探讨如何基于Benford法则对企业的财务数据质量进行评价。

什么是Benford法则？Benford法则，又称为第一位数字法则，是一个数学规律，用于解释数字数据的分布情况。

该法则指出在很多实际生活中的数据集中，数字1出现的概率约为30%，其次是数字2约为17.6%，依此类推，一直到数字9为约4.6%。

这个法则是由美国数学家弗兰克·班福德（Frank Benford）于1938年提出的，并被广泛用于验证数据真实性和进行欺诈检测。

为什么Benford法则适用于财务数据评价？财务数据中包含了大量的数字，比如收入、支出、资产、负债等。

正如Benford法则所描述的，真实的财务数据是在一定规律下生成的，而欺诈或错误的数据则可能不符合这一规律。

利用Benford法则可以对企业的财务数据进行评价，了解其是否符合真实的分布规律，从而评估其质量和真实性。

基于Benford法则的企业财务数据质量评价方法1.数据采集评价企业的财务数据质量首先需要对数据进行采集。

一般来说，财务数据包括收入、支出、利润、资产、负债等各项数据。

这些数据可以从企业的财务报表、会计软件、数据仓库等系统中获取。

在采集过程中需要注意确保数据的完整性和准确性。

2.抽取第一位数字采集到的财务数据经过整理和处理之后，需要抽取每个数字的第一位数字。

对于金额数据123.45，其第一位数字就是1。

这一步骤可以通过Excel等数据处理软件进行简单处理，提取第一位数字并生成新的数据集。

对本福特法则的实证检验作者：张龙逸来源：《中国集体经济》2020年第28期摘要：随着现代化信息技术的进步，大数据在经营中越来越重要。

对于审计人员来说，对数据进行真假辨识是很有必要的。

如果数据失真却没有辨识出来，无疑会对审计工作者造成极大的挑战。

由于本福特定律，揭示了自然形成的数据中数字1～9出现的频率，近年来被国外应用于检测数据异常。

我国可以借鉴此种方法，以此来提高审计人员的效力。

文章试图利用国内全体上市公司的财务报表来验证国内公司财务报表是否有造假的可能性。

关键词：本福特定律;异常数据;审计;大数据的应用一、财务造假的简介当今信息化时代，社会中财务造假的现象可以说是十分常见。

企业的财务造假就是企业对其向外部披露的财务报表进行篡改信息，以此来影响投资者以及信息使用者决策的行为。

财务造假会影响金融市场的健康发展和资源的有效配置，更严重的会引起市场混乱。

2019年，“康得新”公司因财务造假受到了证监会的处罚。

中国证监会通过调查，认定该公司涉嫌在2015～2018年期间，通过虚构销售业务等方式虚增业务收入，并通过虚构采购生产研发费用、产品运输费用等方式虚增营业成本、研发费用和销售费用。

通过上述方式，“康得新”虚增利润总额119亿元。

财务造假的手段常为以下几种：一是编写虚假利润。

企业通过进行投资收益、出卖资产等方式来对利润进行调节，但这种方式属于一次性利润进入，不能实现企业的长久盈利预测。

二是进行虚构交易。

企业利用虚假的原始凭证，在财务报表上捏造不真实的经济事项，使企业的收入和资产出现虚假增加。

三是成本资本化。

企业对不属于资本化的成本进行资本化操作，成本的均摊后就会变相增加了公司的当期利润。

四是故意隐瞒企业关键信息。

上市公司为了获得上市资格，在上市审查时隐瞒关键信息，为了通过证监会的审批还会发布一些虚假信息。

这种手段主要是通过企业和中介公司的聯合，以便于在二级市场上抬升公司的股价。

基于以上财务造假的危害性，本文旨在验证能否能够根据国内全体上市公司的财务数据验证确实存在财务造假，并且提出进一步的解决措施。

使用本福德定律甄别数据造假（Benford’sLaw）数据造假的甄别在数据分析领域是一个热门的话题，也是对数据分析师的一项挑战。

分析数据造假的方法有很多种。

我们在前面的系列文章中曾经介绍过两种检验作弊流量的方法。

一种是根据历史经验及分布情况的多维度交叉检验，另一种是使用随机森林模型根据已知作弊流量的特征对新流量进行分类及预测。

本篇文章介绍一种神奇的数据检验方法，本福德定律(Benford’s Law)。

本福德定律是一种用途广泛的数据检验方法，在安然公司破产和伊朗大选选票甄别中都曾被使用到。

本福德定律通过自然生成的数字中1到9的使用频率对数据进行检验。

如果你的数据具备一定规模，没有人工设定的最大值和最小值，并且数据本身受人为因素影响较小。

那么就可以使用本福德定律对数据进行检验，甄别数据是否经过人为修饰。

本福德定律及公式本福德定律中自然生成的数字首位为1的概率为30.10%，2的概率为17.61%，依次递减，首位为9的概率仅为4.58%。

依据这一期望概率值我们可以对数据进行检验。

以下是本福德定律的计算公式。

通过这一公式可以计算出1-9中每个数字出现数据首位的概率。

举例来说，对于数字9下面的公式可以计算出一组自然生成的数字中9出现在数字首位的概率是多少。

我们使用本福德定律公式逐一计算了数字1-9出现在首位的概率。

以下是每个数字出现的概率值。

后面会根据这一期望的概率值对数据是否进行过人工修改进行甄别。

通过图表可以更较直观的看到本福德定律中每个数字出现的频率以及不同数字间的差异。

与我们想象的不同，数字出现的频率并不是均匀分布的。

1出现的次数为30.10%而9出现的次数仅为4.58%。

下面我们将使用本福德定律对工作中常见的数据进行检验，甄别数据是否经过人为修饰。

广告展现量数据检验首先检验一组广告曝光数据。

下面是某广告一段时间的曝光量数据。

我们将每条展现量数据的第一个数字提取出来，通过本福德定律对这组数据进行检验。