风机的叶尖速比

摘要风力发电是一种清洁能源，通过对风能的利用有利于优化未来的能源利用模式。

本文介绍了风能转换系统最佳叶尖速比控制算法设计，主要目的是实现风力发电系统的最大功率点跟踪。

论文的开始介绍了国内外风力发电的概况，为本文奠定了写作背景。

接着文章阐述了风力发电系统的基本原理，着重介绍了风力机的结构与组成和贝茨理论，这是本文的基础。

紧接着，文章分析了最大功率点跟踪控制算法的基本原理，以及最佳叶尖速比控制的特点，为控制系统的设计做好了准备。

然后针对最佳叶尖速比控制定步长算法的特点，设计出了相应的控制算法和PI控制器，通过选取合适的PI参数，得到了较为理想的追踪效果，从而实现控制所要求的目标。

最后就是本文的重点，Matlab环境下的仿真。

首先我建立了风力发电系统的仿真模型，然后在Matlab环境下实现了最佳叶尖速比控制算法并对控制算法仿真结果进行了分析。

总之，通过分别对风力发电系统的设计和仿真，实现了对风能转换系统最佳叶尖速比控制算法设计。

关键词：风能转换系统；叶尖速比；最大功率点跟踪；PI控制器AbstractWind power is a kind of clean energy, through use of wind energy is beneficial to optimize the mode of energy use in the future. This paper introduces the wind energy conversion system optimal tip speed ratio control algorithm is designed, main purpose is to achieve maximum power point tracking of wind power system .The beginning of the paper introduces the general situation of wind power at home and abroad, laid the writing background for this article. Then the article expounds the basic principle of wind power generation system, emphatically introduces the structure and composition and Bates theory of wind turbine, which is the basis of this article. Then, this paper analyzes the basic principle of the maximum power point tracking control algorithm, and the characteristics of the optimal tip speed ratio control, ready for the design of control system. Then aiming at optimal tip speed ratio control characteristics of fixed step length algorithm, designed the corresponding control algorithm and PI controller, by choosing the right PI parameters, obtained the ideal track effect, so as to realize the goal of control required. The last is the focus of this article, the simulation of Matlab environment. First, I established the simulation model of wind power system, and then realized in Matlab environment the optimal tip speed ratio control algorithm and the control algorithm simulation results are analyzed.In a word, through the design and simulation of wind power generation system, implements the optimal tip speed ratio control algorithm design of wind energy conversion system.Key words:wind energy conversion system;tip-speed ratio;the maximum power point tracking; PI controller目录1 绪论 (1)1.1 引言 (1)1.2 研究的目的和意义 (1)1.3 世界风力发电发展概况 (1)1.3.1 世界风力发电装机容量迅速扩大 (1)1.3.2 风力发电机组的单机容量不断增大 (2)1.3.3 风力发电的经济性日益提高 (2)1.4 我国风力发电发展概况 (2)1.4.1 我国风电利用的特点 (2)1.4.2 我国风电的发展与现状 (3)2 风力发电系统的基本原理 (5)2.1 风力发电机的结构与组成 (5)2.1.1 风力发电机的分类 (5)2.1.2 水平轴风力发电机的结构 (5)2.2 风力发电的基本原理 (8)2.2.1 贝茨（Betz）理论 (8)2.2.2 风力发电机的特性系数 (10)2.3 本章小结 (11)3 最大功率点跟踪算法的基本原理 (12)3.1 最大功率点跟踪算法 (12)3.1.1 风力发电系统的运行区域 (12)3.1.2 最大风能捕获原理 (12)3.2 最佳叶尖速比控制的特点 (14)3.3 本章小结 (14)4 基于叶尖速比PI控制的风力发电系统仿真 (15)4.1 风力发电系统的仿真模型 (15)4.1.1 风速模型的建立 (15)4.1.2 风力发电系统的模型 (16)4.1.3 输出功率追踪控制模型的建立 (17)4.1.3 追踪仿真 (18)4.2 本章小结 (20)5 结束语 (21)参考文献 (22)致谢 (23)1 绪论1.1 引言能源、环境是当今人类生存和发展所要解决的紧迫问题。

叶尖速比在风力机气动设计中的作用及能准确控制最佳叶尖速
比的设计方法
阮志坤
【期刊名称】《风力发电》
【年(卷),期】1989(000)002
【总页数】8页(P6-13)
【作者】阮志坤
【作者单位】无
【正文语种】中文
【中图分类】TK83
【相关文献】
1.垂直轴风力机叶尖速比分析研究 [J], 陈忠维
2.相同叶尖速比不同转速的垂直轴风力机气动性能分析 [J], 黄鹏;王宏光
3.基于最佳叶尖速比的最大风能跟踪在永磁直驱风力发电系统中的实现 [J], 王波;宋金梅;方蒽;刘玮
4.最佳叶尖速比的最大功率自抗扰跟踪控制 [J], 李娟;张克兆;李生权;刘超
5.浅析水平轴风力机叶片设计叶尖速比的选择 [J], 钟贤和;赵萍;曾明伍;李杰
因版权原因，仅展示原文概要，查看原文内容请购买。

独立运行风电机组的最佳叶尖速比控制文 摘：介绍了采用抓极无刷自励发电机的5KW 风电机组的性能特点，采用最佳叶速比控制和稳压控制相结合的控制方法，使风力机在额定风速以下及蓄电池没有充满时按最佳效率运行。

当蓄电池接近充满时，控制风电系统稳压运行，保证蓄电池安全可靠充电。

该风电机组及其控制已实际应用。

1、风机特性大风时通过离心力控制限速弹簧调节叶片角度限制风轮转速风力机的参数：额定功率、启动风速、额定风速、风轮直径、风轮额定转速、齿轮箱增速比、蓄电池标称电压。

风机发电的电气特点：1.1若发电机为异步发电机，其结构简单，控制方便，但需加电容器励磁。

发电机输出的三相交流电压为线电压380V ，要给120V 标称电压的蓄电池组供电，需加变压器降压后，再经整流器整流成直流输出，供蓄电池充电。

整个发电系统环节多，降低了总的运行效率。

1.2原机组采用异步发电机基本恒速运行，在大多数风速情况下不是运行在最佳效率状态。

1.3原风电机组当蓄电池电压达到设定的最高充电电压值时，切断发电机的输出，这一方面使叶片和风轮在切断瞬间承受很大的冲击，容易损坏机组；另一方面在断开发电机输出时蓄电池不一定充满，充电电源已经断开，这样就使蓄电池经常处于充不满状态，缩短其使用寿命。

二、改进后风力发电机2.1风力机最佳运行原理一台风轮半径为R 的风力机，在风速V 下运行时，它所产生的机械功率Pm 为式中p 为空气密度，3V 2A ρ为单位时间穿过风轮扫掠面积的风的能量；Cp 称为风力机的功率系数，实质上也就是风力机将风能转换为机械能的效率。

对于已经设计定型的风力机，Cp 是风轮叶尖线速度与风速之比λ的函数。

λ通常称为叶尖速比。

Cp 与λ的关系曲线是风力机的基本性能之一，且只有λ为某一特定值λm 时，Cp 达到其最大值Cpmax ，所以λm 称为最佳叶尖速比。

为了使风力机产生最大的机械功率，应使Cp 达到其最大值Cpmax 不变，为此，当风速变化时就必须使风力机的转速随风速正比变化，并保持一个恒定的最佳叶尖速比，即：在此条件下，风力机输出最大机械效率，并与风速的三次方成正比，即也即与转速的三次方成正比。

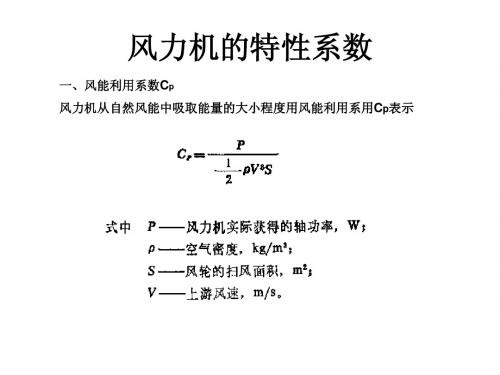
风力发电系统的控制原理风力涡轮机特性：1，风能利用系数Cp风力涡轮从自然风能中吸取能量的大小程度用风能利用系数Cp表示：P---风力涡轮实际获得的轴功率r---空气密度S---风轮的扫风面积V---上游风速根据贝兹〔Betz〕理论可以推得风力涡轮机的理论最大效率为：。

2，叶尖速比l为了表示风轮在不同风速中的状态，用叶片的叶尖圆周速度与风速之比来衡量，称为叶尖速比l。

n---风轮的转速w---风轮叫角频率R---风轮半径V---上游风速在桨叶倾角b固定为最小值条件下，输出功率P/Pn与涡轮机转速N/Nn的关系如图1所示。

从图1中看，对应于每个风速的曲线，都有一个最大输出功率点，风速越高，最大值点对应得转速越高。

如故能随风速变化改变转速，使得在所有风速下都工作于最大工作点，则发出电能最多，否则发电效能将降低。

涡轮机转速、输出功率还与桨叶倾角b有关，关系曲线见图2 。

图中横坐标为桨叶尖速度比，纵坐标为输出功率系统Cp。

在图2 中，每个倾角对应于一条Cp=f(l)曲线，倾角越大，曲线越靠左下方。

每条曲线都有一个上升段和下降段，其中下降段是稳定工作段〔假设风速和倾角不变，受扰动后转速增加，l加大，Cp减小，涡轮机输出机械功率和转矩减小，转子减速，返回稳定点。

〕它是工作区段。

在工作区段中，倾角越大，l和Cp越小。

3，变速发电的控制变速发电不是根据风速信号控制功率和转速，而是根据转速信号控制，因为风速信号扰动大，而转速信号较平稳和准确〔机组惯量大〕。

三段控制要求：低风速段Ｎ＜Ｎｎ，按输出功率最大功率要求进行变速控制。

联接不同风速下涡轮机功率－转速曲线的最大值点，得到ＰＴＡＲＧＥＴ＝ｆ〔ｎ〕关系，把ＰＴＡＲＧＥＴ作为变频器的给定量，通过控制电机的输出力矩，使风力发电实际输出功率Ｐ＝ＰＴＡＲＧＥＴ。

图３是风速变化时的调速过程示意图。

设开始工作与Ａ２点，风速增大至Ｖ２后，由于惯性影响，转速还没来得及变化，工作点从Ａ２移至Ａ１，这时涡轮机产生的机械功率大于电机发出的电功率，机组加速，沿对应于Ｖ２的曲线向Ａ３移动，最后稳定于Ａ３点，风速减小至Ｖ３时的转速下降过程也类似，将沿Ｂ２－Ｂ１－Ｂ３轨迹运动。

浅析水平轴风力机叶片设计叶尖速比的选择
钟贤和;赵萍;曾明伍;李杰
【期刊名称】《东方汽轮机》
【年(卷),期】2010()1
【摘要】设计叶尖速比是风力机叶片设计中需要考虑的重要因素,文中分析了叶尖速比对叶片的弦长、载荷、气动性能、整机的功率和发电量等的影响,讨论了设计叶尖速比的选择。

并分析得出增大设计叶尖速比,能够减小叶片弦长、载荷、成本,提高气动性能,但会使机组发电量有所下降的结论。

【总页数】4页(P31-34)
【关键词】风力机叶片;叶尖速比;气动性能;功率曲线
【作者】钟贤和;赵萍;曾明伍;李杰
【作者单位】东方汽轮机有限公司
【正文语种】中文
【中图分类】TK83
【相关文献】
1.垂直轴风力机叶尖速比分析研究 [J], 陈忠维
2.相同叶尖速比不同转速的垂直轴风力机气动性能分析 [J], 黄鹏;王宏光
3.用叶尖叶片控制水平轴风力机转速的研究 [J], 清水幸丸;蔡千华
4.叶尖速比在风力机气动设计中的作用及能准确控制最佳叶尖速比的设计方法 [J],
阮志坤
5.不同倾斜角叶尖小翼水平轴风力机气动性能 [J], 蔡新;林世发;胡莉;郭兴文因版权原因，仅展示原文概要，查看原文内容请购买。

二■凤轮机的功率及风陡利用系数（・）穿过风轮桨叶扫掠面的风能设：V——风速（指未扰动气流的流速），米/秒；D—风轮直径，米；A——风轮叶片扫掠面枳，米2 ；p—空气密度，千克/米'。

则单位时间内穿过风轮扫掠面积的动能，即功率PA（见图5 — 2）为:图5-2凤轮扫掠面1\ = jA- 千克•米2/秒' （5-1）（二）风能利用系数Cp风能利用系数Cp_ 单位时间内转变为风轮机械能的风惜一单位时问内穿过风轮桨叶扌j掠啲八的全部风能_ 风轮的输出功率一输入风轮面内的功率=—=——-——"一2）风能利用系数是衣征风轮机效率的重要参数•它表明风轮机从风中获得的有用能駅的比例•根据贝茨理论•风能利用系数的最大值为0.593。

关丁贝茨最大值的推导见本章第七节。

水平轴风轮机的C.-0. 2〜0. 5.垂直轴风轮机的C p = 0. 3〜0. 4。

风能利用系数又称功率系数。

(三)风轮的功率风轮的功率即指转变为机械能的功率P=Ca・少人・/ <5-3)由式(5 — 1)和(5 — 3)可以看出*1.当》=常数.pHiye即当凤速•定时.风轮的功率和风轮苴径的平方成正比)"2.当D=常数即当风轮苴径固定时.风轮的功率和风速的立方成正比)"3.当风轮直径、风速不变时，风轮的功率与G，成正比。

4.风轮功率和风轮叶片数无关•但与空气密度成正比。

三、凤轮机的叶尖速比(髙速性系数)在风速为Y时r风轮叶片尖端的线速度与该风速之比称为风轮的高速性系数「高速性系数可表示为：式中入——髙速性系数；3——凤轮在凤速V时的旋转角速度.0,-^1.弧度・秒"；0()——风轮叶片尖处的线速度•弧度・秒'•米；n——转速.转丿分。

所以匸誑TL礬“(5-4)v 30 v由此可知.高速性系数是反映在定风速下风轮转速高低的参数。

高速性系数又称叶尖速比TSR。

四、风轮机的转矩系数风轮的功塞也可以用风轮的转矩与其旋转角速度的乘积来衷示.即P=M • o>式中M——转矩•千克•米；3——旋转角速度.弧度•秒=已知风轮的功率p=寻pD2/・C P所以P —M •(u=-^-pI)2 v1• C5,1 对于某-风轮来说•只是在入为某一数值•即九时•才达到最大G值（（・：“）•如图5 — 3所示■在入工為时・Cp值下降a或则定义称为转矩系数侧M=C M - （fRAv1 2 3）.即当风轮尺寸（R）固定时，在一定风速下心是一个反映转矩大小的系数。

风能利用系数是评价风力发电机性能的重要指标之一。

在设计风力发电机的过程中，需要综合考虑多个因素，其中包括叶尖速比和桨距角。

这两个参数都对风能利用系数有着重要的影响，下面我们将分析它们与风能利用系数之间的函数关系。

一、叶尖速比的影响叶尖速比是风力发电机叶片末端的线速度与风速之比。

通常情况下，叶尖速比的取值范围在5-9之间。

而叶尖速比对风能利用系数的影响是非常显著的。

当叶尖速比过大时，风力发电机叶片的阻力将会增大，从而导致风能利用系数下降。

而叶尖速比过小时，叶片的转动效率也会下降，同样会导致风能利用系数的降低。

叶尖速比与风能利用系数的函数关系可以用一个类似抛物线的曲线来描述。

随着叶尖速比的增加，风能利用系数先增加后减小，存在一个最大值点。

二、桨距角的影响桨距角是指风力发电机叶片相对于风向的角度。

它对风能利用系数也有着重要的影响。

当桨距角过小时，叶片受风面积减小，受风面积受风能利用系数也会下降。

而当桨距角过大时，叶片的承受风压面积增大，同样会导致风能利用系数的减小。

桨距角与风能利用系数也呈现出类似抛物线的函数关系。

三、风能利用系数的函数关系根据叶尖速比和桨距角对风能利用系数的影响，可以得出风能利用系数与叶尖速比和桨距角之间具有函数关系。

在实际的工程设计中，通常需要对叶尖速比和桨距角进行综合考虑，通过数值模拟和实验验证，得出最佳的风能利用系数对应的叶尖速比和桨距角。

四、结语风能利用系数与叶尖速比和桨距角之间的函数关系是风力发电机设计中一个重要的研究课题。

通过合理地选择叶尖速比和桨距角，并综合考虑风动力特性、结构强度和材料成本等多个因素，可以提高风力发电机的发电效率和经济性。

希望未来能够进一步深入研究风能利用系数与叶尖速比和桨距角之间的函数关系，为风力发电行业的发展做出更大的贡献。

风力发电作为清洁能源发电的重要来源，其发电效率和经济性一直备受关注。

在风力发电机的设计和运行中，风能利用系数作为衡量风力发电机性能的重要指标之一，对于提高风力发电机的发电效率具有重要意义。

变桨距风电机组最佳叶尖速比的拟合求取张仰飞;李海峰;王伟胜;王瑞明;李少林【摘要】Based on the wind turbine mathematical model, the expression of the optimal blade tip speed ratio was deduced through analysis of the maximum wind power tracking conditions. The curve-fitting method was used to obtain the expression parameters of the optimal blade tip speed ratio when there were measurement errors. Then, the optimal blade tip speed ratio could be indirectly calculated. An example shows that thefitted data have high accuracy. This study provides a new curve-fitting method for calculating the optimal blade tip speed ratio of wind turbines.%根据风力机数学模型,分析最大风能捕获的运行点条件,推导最佳叶尖速比的计算表达式.运用曲线拟合方法拟合得到误差数据条件下的最佳叶尖速比的参数,间接计算得到最佳叶尖速比算例显示拟合值准确度较高.研究工作为计算风电机组最佳叶尖速比提供新的曲线拟合方法.【期刊名称】《河海大学学报（自然科学版）》【年(卷),期】2012(040)002【总页数】4页(P229-232)【关键词】风力发电机组;最佳叶尖速比;拟合求解方法【作者】张仰飞;李海峰;王伟胜;王瑞明;李少林【作者单位】中国电力科学研究院新能源研究所,北京100192;南京工程学院电力工程学院,江苏南京211167;江苏省电力公司调度与通信中心,江苏南京210024;中国电力科学研究院新能源研究所,北京100192;中国电力科学研究院新能源研究所,北京100192;中国电力科学研究院新能源研究所,北京100192【正文语种】中文【中图分类】TK83风能密度低，风速变化频繁，风电机组变桨距技术应运而生，其实现方式[1-8]如下:通过对适时风速的测量，逻辑判断风速是低于额定风速还是高于额定风速.当风速低于额定风速时，桨叶的迎风角(桨距角)为0°，使桨叶能够最大限度地吸收风能;当风速高于额定风速时，桨距调节装置调节桨叶的迎风角，降低并保持吸收的风能在额定值，从而保证机组输出恒定(额定)的功率.由于风力机(风轮)特殊的空气动力学特性，即使桨距角保持为0°也不能保证机组一定在最大风能捕获状态运行，必须通过机组的转速控制使机组转速和风速的比值尽可能保持在一个合理的定值——最佳叶尖速比，才能使机组吸收到最大的机械功率，这样的控制过程就是最大风能捕获控制.对风电机组而言，如何准确估算其最佳叶尖速比(即控制目标)，对于机组是否能够实现最大风能捕获控制，提高机组的发电效益，具有十分重要的意义.笔者研究在测量数据有误差条件下的最佳叶尖速比求取问题，发现数据拟合方法结合特定的数学计算可以较准确地获得最佳叶尖速比.1 变桨距风力机的数学模型变桨距风力机模型[1-2]如下:其中式中:C P——风能捕获系数;ρ——空气密度，kg/m3;S——叶轮扫过的面积，m2，S=πR2;v——叶轮的上游风速，m/s;P W——风力机吸收的机械功率;c1～c9——风力机参数(独立参数只有8个);λ——叶尖速比，即叶片的叶尖线速度与风速之比——中间变量;β——桨距角;R ——风轮半径;n——风轮转速;ω——转子的电角速度.2 最大风能捕获的运行点条件β=0°时，变桨距风力机 C P～λ曲线如图 1所示.对特定的风力机，其捕获的风能与转速、风速、空气密度等有关.由式(1)～(4)，对应于某个最佳叶尖速比λ0会有1个最大的风能捕获系数C Pmax，从而使风力机运行于最大风能捕获点P Wmax.显然，最大风能捕获运行点是=0或=0，也即=0或=0.图1 β=0°时变桨距风力机C P～λ曲线Fig.1 C P～λcurve of variable-blade wind turbine under condition ofβ=0°3 最佳叶尖速比的拟合求取思路工程实际中，对应于低于额定风速的某一个风速v0，根据式(1)，期望风力机吸收的机械功率为P W=C PmaxρS.可见，在风速一定时，风力机能吸收多少机械功率取决于风能吸收系数C P的大小，也就是取决于风轮的转速或者是叶尖速比λ的大小.β=0°时可推导得即令 A=c2 c1exp(c7 c9)，B=(c2 c9+c6)c1exp(c7 c9)，则工程中可由式(1)及测量或计算的P W，ρ，v，ω，S来计算风能捕获系数C P，因 P W，ρ，v，ω，S的测量或计算难免存在一定的误差，必然会导致C P也有一定的误差.针对该C P存在误差的情况，如何求得对应于P Wmax的λmax，由式(10)可知，如果能求得 c7，A 和B ，则λmax可求 .4 算例分析参考文献[9-13]，设定1组参数:c1=0.32，c2=116，c3=0.4，c4=0.4，c5=0.1，c6=1.7425，c7=21，c8=0.08，c9=0.035.计算得 A=77.4131 ，B=3.87232，C=c7=21，λmax=10.241651.分析 C P 值在一定误差条件下通过曲线拟合的方法求解λmax的准确度.图2 无误差C P数据拟合曲线Fig.2 Fitting curve of C P without errors图3 ±10%误差C P数据拟合曲线Fig.3 Fitting curve of C P with±10%e rror5 问题讨论5.1 β≠0°时的情况前文针对的是β=0°时问题的推导，工程实际中因桨距角直接影响机组的吸收功率，从而影响机组的出力，各厂家对机组的0°桨距角都会进行严格的校正.图4是2种机型变桨距机组低于额定风速时桨距角的实测结果，数据拟合结果如图中的线条所示.图4(a)中，β＞0.3°以上的数据分散特性明显，不符合桨距的机械惯性特征，可以判断是测量噪声.图4(b)中，0.14°＞β＞0.1°.图4 机组低于额定风速时桨距角的实测结果Fig.4 Measured blade angle of wind turbines with speed lower than rated wind velocity按照上述算例中的参数设定，可得β=0°和β=0.5°时C P～λ曲线(图5).从图5可以看出2条曲线相差很小，最大点相差不到7%.可见，上述分析结论可以推广作为β≈0°时的情况使用.5.2 风速v测量值的误差影响风电机组利用计算机每秒采集1次来自风速仪的数据，每10min计算1次平均值，用于判断启动风速和停机风速，这样的风速数据并不精确，不能用来产生功率曲线[2].作为控制目标，也不能用该测量值通过式(4)来计算λ.相对而言，机组的转速能较准确地测量=0运行点可以通过调节系统的多次正调节和反调节实现，显然如果记录特定风速时的足够多组P Wmax及ω值就可以按照本文的方法拟合得到机组的λmax值，从而在后续的调节过程中不需要不断地正反调节.6 结语本文分析中叠加的误差数据为服从正态分布的随机数据，由拟合结果来看，±10%误差C P数据拟合所得的A，B，C值和计算的λmax值都比较准确，工程上如果得到一定精度的C P数据即可以用上述方法拟合求解得高精度的λmax，从而为最大风能捕获控制获得必需的目标参数.用拟合方法求取最佳叶尖速比，要求数据具有一定的数量和密度，倘若数据的代表性不够则拟合误差就会增大.辨识研究的目的之一是为控制需求提供准确的参数.研究工作表明:辨识工作可以根据应用目标的需要作适当调整，可以不辨识风力机的全部8个参数，只辨识部分参数的组合结果就能够满足控制目标实现的需要.参考文献:图5 β=0°和β=0.5°时的 C P～λ曲线Fig.5 C P～λcurves under conditions of β=0°and β=0.5°[1]叶杭冶.风力发电机组的控制技术[M].北京:机械工业出版社，2008.[2]霍志红，郑源，左潞，等.风力发电机组控制技术[M].北京:中国水利水电出版社，2010.[3]WU Feng，ZHANG Xiao-ping，GODFREY K，et al.Modeling and controlof wind turbine with doubly fed induction generator[R].Georgia:PSCE，2006:1404-1409.[4]MUHANDO E B，SENJYU T，YONA，A，et al.Disturbance rejection by dual pitch control and self-tuning regulator for wind turbine generator parametric uncertainty compensation[J].Control Theory&Applications，IET，2007，1(5):1431-1440.[5]WU Feng，ZHANG Xiao-Ping，JU Ping.Modeling and control of the wind turbine with the direct drive permanent magnet generator integrated to power grid[R].Nanjing:DRPT，2008:57-60.[6]刘军，何玉林，李俊，等.变速变桨距风力发电机组控制策略改进与仿真[J].电力系统自动化，2011，35(5):82-85.(LIU Jun，HE Yu-lin ，LIJun，et al.Design and simulation of an improved control strategy for variable-speed pitch controlled wind turbine driven generator system[J].Automation of Electric Power Systems，2011，35(5):82-85.(in Chinese))[7]李立成，叶林.变风速下永磁直驱风电机组频率-转速协调控制策略[J].电力系统自动化，2011，35(17):26-31.(LI Licheng，YE Lin.Coordinated control of frequency and rotational speed for direct drive permanent magnet synchronous generator wind turbine at variablewind speeds[J].Automation of Electric Power Systems，2011 ，35(17):26-31.(in Chinese))[8]宋卓彦，王锡凡，滕予非，等.变速恒频风力发电机组控制技术综述[J].电力系统自动化，2011，35(10):8-17.(SONG Zhuoyan，WANG Xi-fan，Teng Yu-fei，et al.Overview of control technologies for variable-speed constant-frequency wind turbines[J].Automation of Electric Power Systems，2011，35(10):8-17.(in Chinese))[9]MONROY A ，ALVAREZ-ICAZA L.Real-time identification of wind turbine rotor power coefficient[R].San Diego:PICDC，2006:3690-3696.[10]SENJYU T，OCHI Y，YONA A ，et al.Parameter identification of wind turbine for maximum power point tr acking control[R].Seoul:PICEMS，2007:248-252.[11]THOMSENS ，ROTHNHAGENK ，FUCHSFW.Onlineparame ter identificationmethods for doubly fed induction generators[R].Rhodes:PESC，2008:2735-2741.[12]IRIBAS-LATOURM ，LANDAU I D.Closed loop identification of wind turbines models for pitch control[R].Makedonia:MCCA，2009:1263-1268. [13]AIMANIS E.Practical identification of a DFIG based wind generator model for grid assessment[R].Ouarzazate:ICMCS，2009:278-285.[14]王正林，王胜开，陈国顺，等.MATLAB/Simulink与控制系统仿真[M].北京:电子工业出版社，2008.【相关文献】a.C P数据运用Matlab拟合函数[14]f(x)=(A/x-B)exp(-C/x)拟合，求得 A=77.41，B=3.872，C=21，拟合结果精确，拟合曲线如图2所示，2条曲线重合，看不出差别.根据拟合结果求得λmax=10.241874.b.C P计算数据叠加±10%随机误差时，同样运用Matlab拟合函数f(x)=(A/x-B)exp(-C/x)，拟合求得 A=77.55，B=3.878，C=21.03，拟合曲线如图3所示.拟合结果令人满意，由拟合的 A，B和C值计算得λmax=10.25036.该结果与设定值相差很小，仅为0.00085%.。