2.3 匀变速直线运动的位移与时间的关系

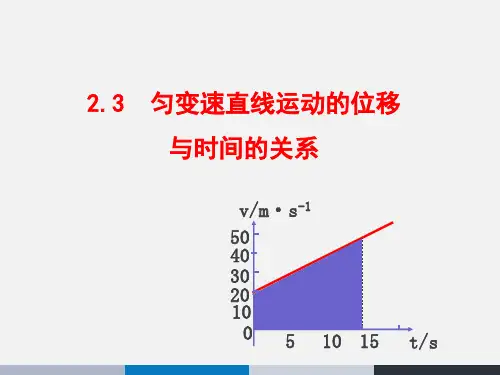
第三节匀变速直线运动的位移与时间的关系一、位移时间公式1、推导：①图像法：（由v-t图像求位移）---微元的思想结论：做匀变速直线运动的物体的位移对应着v－t图象中的图线与对应的时间轴所包围的面积．即：位移与时间关系式：x＝v0t＋12at2.②解析法：（由平均速度求得）⎪⎪⎩⎪⎪⎨⎧+=+==atvvvvvt vxtt2得：x＝v0t＋12at2.2、物理意义：在匀变速直线运动中位移随时间变化的规律。

3、注意：①适用范围：匀变速直线运动。

②决定关系：位移的决定式，即匀变速直线运动中位移是由初速度、加速度、时间共同决定。

③比例关系：二次关系，也叫非线性关系。

④同一性：x、a、v0、vt具有同一性。

⑤合理性：已知位移反求时间，可能有两个值，要合理取舍。

二、速度--时间公式应用1、使用方法：①判断：运动性质（a为定值）。

②确定：研究对象和研究过程。

③设定：正方向（一般初速度的方向为正方向，无初速度则选择加速度为正方向）。

④公式应用：x＝v0t＋12at2；（此式子为矢量式，应将方向带入求解）⑤结果：结果如何为矢量，大小方向都需要求解。

2、例子：已知一个物体以向西的初速度4m/s做匀变速直线运动，其加速度大小为2m/s2，求1s末、2s末、4s末、8s末的速度和位移和路程，如果该物体是汽车，则结果又将如何？．三、推论1、逐差相等原理：在匀变速直线运动中，相邻相等的时间间隔位移之差是一个定值。

表达式：△x=aT 2．推导：⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=212022019213421221T a T v x T a T v x aT T v x ⎪⎪⎩⎪⎪⎨⎧+=-+=-20232012521321T a T v x x T a T v x x 2aT x =∆ 2、比例关系：初速度为零的匀加速直线运动中①在前T ，前2T ，前3T 的位移之比1:4:9……n2②在第T ，第2T ，第3T 的位移之比1:3:4……（2n-1） 3、逆向思维法：末速度为零的匀减速直线运动可以看做反向的初速度为零的匀加速直线运动。

2.3匀变速直线运动的位移与时间的关系（考点解读）（原卷版）考点1 匀变速直线运动位移与时间的关系1、匀变速直线运动的位移与时间的关系式：x ＝v 0t ＋12at 2。

2、公式的推导（1）利用微积分思想进行推导：在匀变速直线运动中，虽然速度时刻变化，但只要时间足够小，速度的变化就非常小，在这段时间内近似应用我们熟悉的匀速运动的公式计算位移，其误差也非常小，如图所示。

（2）利用公式推导：匀变速直线运动中，速度是均匀改变的，它在时间t 内的平均速度就等于时间t 内的初速度v 0和末速度v 的平均值，即x ＝12(v 0＋v )t 。

结合公式v ＝v 0＋at 可导出位移公式：x ＝v 0t ＋12at 2，当初速度为0时，x ＝12at 2。

3、技巧归纳（1）在v －t 图像中，图线与t 轴所围的面积对应物体的位移，t 轴上方面积表示位移为正，t 轴下方面积表示位移为负。

（2）位移公式x ＝v 0t ＋12at 2只适用于匀变速直线运动。

（3）公式中x 、v 0、a 都是矢量，应用时必须选取正方向；一般选v 0的方向为正方向．当物体做匀减速直线运动时，a 取负值，计算结果中，位移x 的正负表示其方向。

（4）当v 0＝0时，x ＝12at 2，即由静止开始的匀加速直线运动的位移公式，位移x 与t 2成正比。

4、匀变速直线运动中的平均速度该段时间的末速度v=v t +at ，由平均速度的定义式和匀变速直线运动的位移公式整理加工可所以在匀变速直线运动中，某一段时间内的平均速度等于该段时间内中间时刻的瞬时速度，又等于这段时间内初速度和末速度的算术平均值。

5、匀变速直线运动推论公式：任意两个连续相等时间间隔T 内，位移之差是常数，即△x=x 2-x 1=aT 2．拓展：△x MN =x M -x N =（M-N ）aT 2。

推导：如图所示，x 1、x 2为连续相等的时间T 内的位移，加速度为a 。

考点2 匀变速直线运动速度与位移的关系 1、匀变速直线运动位移与速度的关系。

第2.3课 匀变速直线运动的位移与时间的关系一、匀速直线运动的位移 1.位移公式：x ＝ .2.位移在v －t 图象中的表示：对于匀速直线运动，物体的位移在数值上等于v －t 图线与对应的时间轴所包围的矩形的_____.如图1所示，阴影图形的面积就等于物体在t1时间内的_____.二、匀变速直线运动的位移1.位移在v －t 图象中的表示：做匀变速直线运动的物体的位移对应着v －t 图线与时间轴所包围的_________.如图所示，阴影图形的面积等于物体在t1时间内的_____.2.公式：x ＝_________.三、位移—时间图象（x －t 图象）1.x －t 图象：以______为横坐标，以______为纵坐标，描述位移随时间的变化规律.2.常见的x －t 图象：（1）静止：一条______________的直线. （2）匀速直线运动：一条_____的直线. 3.x －t 图象的斜率等于物体的 .答案：vt 面积 位移 梯形面积 位移 2021at t v 时间t 位移x 平行于时间轴 倾斜 速度考点一 对位移公式2012x v t at =+的进一步理解（1）反映了位移随时间的变化规律。

（2）因为0v 、a 、x 均为矢量，使用公式时应先规定正方向。

一般以0v 的方向为正方向。

若a 与0v 同向，则a 取正值；若a 与0v 反向，则a 取负值； 若位移计算结果为正值，说明这段时间内位移的方向为正；若位移计算结果为负值，说明这段时间内位移的方向为负。

（3）因为位移公式是关于t 的一元二次函数，故x t -图象是一条抛物线（一部分）。

但它不表明质点运动的轨迹为曲线。

（4）对于初速度为零（00v =）的匀变速直线运动，位移公式为21122x vt at ==，即位移x 与时间t 的二次方成正比。

【注意】（1）2012x v t at =+是矢量式，应用时x 、0v 、a 都要根据选定的正方向带上“+”、“—”号。