当前位置：文档之家 › §5-1 角动量与力矩 第五章 角动量变化定理与角动量守恒 Z O

§5-1 角动量与力矩 第五章 角动量变化定理与角动量守恒 Z O

  • 格式：pdf
  • 大小：249.85 KB
  • 文档页数：4

下载文档原格式

  / 4

合集下载

第五章 角动量 角动量守恒(2011)

第五章 角动量 角动量守恒(2011)
在中国航天事业中做出杰出贡献的哈工大人： 在中国航天事业中做出杰出贡献的哈工大人：
.中国载人航天工程副总指挥——胡世祥 中国载人航天工程副总指挥——胡世祥 胡世祥，1940年生 黑龙江人，毕业于哈尔滨工业大学 年生， 胡世祥，1940年生，黑龙江人，毕业于哈尔滨工业大学 控制工程系。 控制工程系。 曾任中国酒泉卫星发射中心副总工程师， 曾任中国酒泉卫星发射中心副总工程师，西昌卫星发射 中心副主任、主任。 中心副主任、主任。 长期从事火箭卫星发射试验，主持发射过多种型号卫星， 长期从事火箭卫星发射试验，主持发射过多种型号卫星， 曾多次担任卫星发射现场的 总指挥。 总指挥。 现任总装备部副部长，中国载人航天工程副总指挥， 现任总装备部副部长，中国载人航天工程副总指挥，主 神舟”号飞船发射工作。 管“神舟”号飞船发射工作。
（2） 对 O 点的角动量 ）
r r r r = r′ + R r r r r r r r r r r L = r × p =(R+r′)× p= R× p = R×m t g O r r L = Rm gt R ⊥g O
m r m v
确定质点有无角动量，要看位矢是否存在绕参考点的转动。 确定质点有无角动量，要看位矢是否存在绕参考点的转动。
老校长杨士勤曾说： 老校长杨士勤曾说： 神舟号”飞船研制过程中， 在“神舟号”飞船研制过程中，有5项关键技术 是由哈工大教师 是由哈工大教师 做出的成果解决的。 做出的成果解决的。 超大型空间环境模拟器； 超大型空间环境模拟器； 仿真试验OUT型闭式转台 型闭式转台； 仿真试验OUT型闭式转台； 飞船数据管理容错计算机； 飞船数据管理容错计算机； 返回舱焊接变形控制技术； 返回舱焊接变形控制技术； 飞船故障诊断专家系统。 飞船故障诊断专家系统。 国产舱外航天服 失重训练模拟水槽 出舱用反光镜体 舱外航天服试验舱

第5章-角动量角动量守恒定律

第5章-角动量角动量守恒定律

② 在点2处
2
力矩 M 2
力矩定义式 M r v
P
{ 方向：垂直图平面向里， 大小； M 2 Gm0m / R
R
m
900
m0
1

角动量 L2
同上理可得 m 的速度v2 Gm0 / R
{
方向：垂直图平面向外，
L2
大小； L2 m Gm0 R
例4、地球在远日点时，它离太阳的距离为r1 1.52 1011 m，
子从静止开始以速度 v 相对绳子向上爬，求重物上升
的速度。
(复习题一、三. 19)
解 设猴子、重物对地面的速度分别为 v1、v 2 。
由猴、重物组成的系统角动量守恒，得
v1 v2
R
∵ v1 v猴绳 v绳-地 v v绳-地
v1
v2
而 v绳地 v物地 v2 , 则 v1 v v2
物体运动仅受有心力作用时， 力对力心 O点的力矩始终为零。
m 有心
在有心力作用下，运动物体
r 力F
对力心 O 的角动量守恒。
力心o
L1 L2
r1

mv1

r2

mv2
行星绕太阳运动：
引力指向太阳，行星在引
力动的(，力有而矩心且为力零)r作，//F用M，下对r绕 力太F心阳O0运,
，且有
d
2 2

d12

d
2 3
，试求：(1)小球所受重
{ 力相对 A,
解 (1) MA
B力, 矩C 的M力矩r；
(2)小球相对 F
方向：垂直图平面向里，
大小；

角动量与角动量定理

角动量与角动量定理
rr pr
1
L
dt 2 dt 2 dt 2
2m
2m
太阳对行星的引力总是指向太阳，因而行星对太阳
中心的角动量守恒，L为常量，所以得证。
L rmv mr2
方向 垂直于圆面
② 质点作匀速直线运动时，角 动量守恒。
L rmv sin mvd
方向始终垂直纸面向外
r L
r pr r
O
Or
r
d
pr
③ 角动量与参考点的位置有关。
r L
因而在说明一个质点的角动量
pr
时，必须指明是相对于哪一个 参考点而言的。
O
rr
θ m
锥摆 O
l
m
O
v
且在高速低速范围均适用。
例题1：
证明行星运动的开普勒第二定律：行星对太阳
的矢径在相等的时间内扫过的面积相等。
r
L
解：行星位矢扫过的面积dS
dS
1
r
r dr
sin
1
rr drr
dS r
2
2
单位时间行星位矢扫过的面积
•
drr
dS 1 rr drr 1 rr drr 1 rr vr 1
vr
y
xp z
L z
xp y
yp x
L , L , L 分别称为角动量在x、y、z轴上的分 x yz
量式，或称为对x、y、z轴的角动量。
二、力矩
1、定义
力
r F
对参考点O

rr
r F
r
M
r
rr
F
θ
Or
m
大小：
M
rF
sin

角动量定理及角动量守恒定律

角动量定理及角动量守恒定律

精品文档，知识共享！！！角动量定理及角动量守恒定律一、力对点的力矩：如图所示，定义力F对O 点的力矩为： F r M ⨯=大小为： θsin Fr M ＝ 力矩的方向：力矩是矢量，其方向可用右手螺旋法则来判断：把右手拇指伸直，其余四指弯曲，弯曲的方向由矢径通过小于1800的角度转向力的方向时，拇指指向的方向就是力矩的方向。

二、力对转轴的力矩：力对O 点的力矩在通过O 点的轴上的投影称为力对转轴的力矩。

1）力与轴平行，则0=M；2）刚体所受的外力F在垂直于转轴的平面内，转轴和力的作用线之间的距离d 称为力对转轴的力臂。

力的大小与力臂的乘积，称为力F对转轴的力矩，用M表示。

力矩的大小为： Fd M ＝ 或： θsin Fr M ＝其中θ是F 与r的夹角。

3）若力F 不在垂直与转轴的平面内，则可把该力分解为两个力，一个与转轴平行的分力1F，一个在垂直与转轴平面内的分力2F ，只有分力2F才对刚体的转动状态有影响。

对于定轴转动，力矩M的方向只有两个，沿转轴方向或沿转轴方向反方向，可以化为标量形式，用正负表示其方向。

三、合力矩对于每个分力的力矩之和。

合力 ∑=i F F合外力矩 ∑∑∑=⨯=⨯=⨯i i i M F r F r F r M＝即 ∑i M M＝四、质点的角动量定理及角动量守恒定律在讨论质点运动时，我们用动量来描述机械运动的状态，并讨论了在机械运动过程中所遵循的动量守恒定律。

同样，在讨论质点相对于空间某一定点的运动时，我们也可以用角动量来描述物体的运动状态。

角动量是一个很重要的概念，在转动问题中，它所起的作用和(线)动量所起的作用相类似。

在研究力对质点作用时，考虑力对时间的累积作用引出动量定理，从而得到动量守恒定律；考虑力对空间的累积作用时，引出动能定理，从而得到机械能守恒定律和能量守恒定律。

至于力矩对时间的累积作用，可得出角动量定理和角动量守恒定律；而力矩对空间的累积作用，则可得出刚体的转动动能定理，这是下一节的内容。

第五章角动量定理

第五章角动量定理

p是动量， 是动量与径向夹角。
角动量定理
Mz
dJ z dt
（右手法则为正）
直角坐标系中， Jz可表示为
p py cos px sin
Mz=0,角动量守恒
J z p py cos px sin x py y px
积分形式
t2
M zdt
t2 Jzdt J z2 J z1
§5.4 有心力 掌握有心力场中运动的基本方程；利用有 效势能曲线，定性讨论运动轨道；利用基本方程，解出行 星的轨道方程。
§5.1 质点的角动量定理
一. 力矩
以二维 平面纯转动为例。
z
f
外力 f 作用于质点m，考察
其作功与角位移d的关系。
m
在极坐标系中对纯转动作功
O
x
dA f dr ( f eˆ f eˆ ) (d eˆ d eˆ )
哥白尼(N. Copernicus)日心说
Portrait, 1580, Toruń Old Town City Hall
第谷(Tycho Brahe)的观测数据，开普勒(J. Kepler)的分 析拟合。
Internet Keplaw
开普勒行星运动三定律 行星沿椭圆轨道绕太阳运行，太阳位于椭圆两焦点之 一。轨道定律
行星对太阳的矢径在相等的时间内扫过相等的面积。 面积定律
各行星公转周期的平方正比于其轨道半长轴的立方。 周期定律
二. 万有引力定律 牛顿提出平方反比引力解释开普勒定律。
设行星绕日轨道近似为圆周，由面积定律，必是匀速圆
周运动，加速度 a v2 r
注意到 v 2r ，并利用开普勒第三定律 T r3/ 2
f f
f
O Larm

角动量变化定理

角动量变化定理

理学院物理系陈强第5章角动量变化定理与角动量守恒§5-1. 角动量与力矩§5-2. 质点的角动量变化定理角动量守恒§5-3.质点组的角动量变化定理角动量守恒§5-4.有心运动12理学院物理系陈强第5章角动量变化定理与角动量守恒一.质点的角动量(动量矩)v m r p r L r r r r r ×≡×≡又称动量矩Oαdpr L1.定义：在惯性参考系中选一固定的参考点O ，运动质点对O 点的位矢r ,动量为p ,则质点对O 点的角动量为:mvdsin rmv sin rp L ===ααα为r 和p 两矢量间的夹角角动量L 的大小：§5-1. 角动量与力矩垂直于矢径r 和动量p 所组成的平面，角动量L 的方向：指向由右手螺旋法则确定.3理学院物理系陈强第5章角动量变化定理与角动量守恒mαO L = rmvL r v例：•角动量的大小和方向不仅决定于质点的运动也依赖于所选定的参考点，参考点不同，质点的动量矩不同。

注意:•角动量的单位千克·米2/秒（kg ·m 2/s)水平面上质点做匀速圆周运动4理学院物理系陈强第5章角动量变化定理与角动量守恒例如：vr r r m r L om O ×=vlm L O =方向变化v r r r m r L m o O ×=′′αsin v lm L O =′方向竖直向上不变O l αv r O ′锥摆m5理学院物理系陈强第5章角动量变化定理与角动量守恒2.角动量的分量表示v m r p r L rr r r r ×≡×≡在直角坐标系中：yz y z x m z ym zp yp L v v −=−=zx x y m zm zp L v v x xp z −=−=xy x y z m y xm yp xp L v v −=−=()z y x z y x p p p zy x k j i L ,L ,L r rr =kL j L i L L z y x rrrr ++==L r6理学院物理系陈强第5章角动量变化定理与角动量守恒二.力矩即F r M r r r ×=力矩的大小：Fr sin rF M 0==ααsin r r 0=——称力臂。

第五章 角动量角动量守恒定理解读

第五章 角动量角动量守恒定理解读

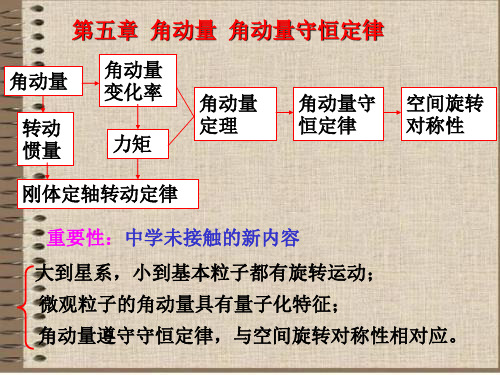
第五章角动量角动量守恒定理本章结构框图学习指导本章概念和内容是中学没有接触过的，是大学物理教学的重点和难点。

许多同学容易将平动问题与转动问题中的概念和规律混淆，例如两种冲击摆问题。

建议采用类比方法，对质量与转动惯量、动量与角动量、力与力矩、冲量与角冲量、平动动能和转动动能、运动学的线量和角量、动量定理和角动量定理、动量守恒和角动量守恒……一一加以比较。

本章的重点是刚体定轴转动问题，注意定轴条件下，各种规律都应该用标量式表示。

还请注意动量守恒在天体问题、粒子问题中的应用。

基本要求1.理解质点、质点系、定轴刚体的角动量概念。

2.理解定轴刚体的转动惯量概念，会进行简单计算。

3.理解力矩的物理意义, 会进行简单计算。

4.掌握刚体定轴转动定律，熟练进行有关计算。

5.理解角冲量（冲量矩）概念，掌握质点、质点系、定轴刚体的角动量定理，熟练进行有关计算。

6.掌握角动量守恒的条件，熟练应用角动量守恒定律求解有关问题。

内容提要1.基本概念刚体对定轴的转动惯量：是描述刚体绕定轴转动时，其转动惯性大小的物理量。

定义为刚体上每个质元（质点、线元、面元、体积元）的质量与该质元到转轴距离平方之积的总和。

即：I的大小与刚体总质量、质量分布及转轴位置有关。

质点、质点系、定轴刚体的角动量：角动量也称动量矩，它量度物体的转动运动量，描述物体绕参考点（轴）旋转倾向的强弱。

表5.1对质点、质点系、定轴刚体的角动量进行了比较。

表5.1质点、质点系和定轴刚体的角动量力矩：力的作用点对参考点的位矢与力的矢积叫做力对该参考点的力矩（图5.1）：即：大小：（力×力臂）方向：垂直于决定的平面，其指向由右手定则确定。

对于力矩的概念应该注意明确以下问题：•区分力对参考点的力矩和力对定轴的力矩：力对某轴的力矩是力对轴上任意一点的力矩在该轴上的投影。

例如：某力对x、y、z轴的力矩就是该力对原点的力矩在三个坐标轴上的投影：由上可知：力对参考点的力矩是矢量，而力对定轴的力矩是代数量。

角动量 冲量矩 角动量守恒定律

角动量 冲量矩 角动量守恒定律
力的时间累积效应： 冲量、动量、动量定理．
力矩的时间累积效应： 冲量矩、角动量、角动量定理．
41..4.质1 点质的点角的动角量动量定理和角动量z守L恒定v律
度
v
质量为m 的质点以速
在空间运动，某时对
O 的位矢为 r ，质点对O
rm
xo
y
的角动量
L

r

p

r

mv
L

1 2
mv 12

r1 r2
2

1

4.4.2 刚体定轴转动的角动量定理
和角动量守恒定律
1 刚体定轴转动的
角动量

L
mi ri 2
i
(
miri2 )
L

Ji
z

O ri
v i
mi
2 刚体定轴转动的角动量定理
质M点i mi受dd合Lti力矩dM(diJ(t包 )括Midedxt、(mMiiirni
t2
t1
Mdt

J 22

J11
当转轴给定时，作用在物体上的冲量矩等于在
这段时间内转动物体的角动量的增量
例 在通过定滑轮的一条轻绳的两 端，分别连有质量为 m1和 m2的物体， 设滑轮是质量为M 、半径为R的质 量均匀分布的圆盘。设绳的质量可 不计，求两物体的加速度。 解： 支撑力与滑轮的重力皆通原 点。只有 m1和m2 的重力才有对原 点的力矩。
R
M
m 1
m 2
作用于该系统的力矩为
M Rm1g Rm2g m1 m2 Rg
整个系统的角动量为
L

5-1-角动量-角动量守恒定律

5-1-角动量-角动量守恒定律

M
N
The End
Ex9. 均匀细棒OA可绕通过其一段O而与棒垂直 的水平固定光滑轴转动，如图所示。今使棒从 水平位置由静止开始自由下落，在棒摆到竖直 位置的过程中，下述说法正确的是 （ ） （A）角速度从小到大，角加速度不变 （B）角速度从大到小，角加速度从小到大 （C）角速度从小到大，角加速度从大到小 （D）角速度不变，角加速度为零 O A
Fi mr(2 )
2
N
f Fi
mg sin f Fi cos mg cos Fi sin N
min

1 2 g (sin cos ) r (cos sin )
r
f N

G
mg sin f Fi cos mg cos Fi sin N
2
1 dS r dr sin r dr 2 2 1 1 dt 1 Ldt r v dt r p 2 2 m 2 m 1
例2.
发射一宇宙飞船去考察一质量为 m1 ，半径 为 R 的行星，当飞船静止在空间距行星 4 R时， 以速度 v0 发射一质量为 m2 的仪器（m2远小于 飞船质量），要使该仪器刚好掠着行星表面着 陆， 角应是多少？着陆滑行初速度为多大？
例５：试求作用在圆锥摆上的拉力T、重力mg 和合力F对o’点、o 点、oo’ 轴的力矩，并判断 小球对o’ 点、o 点、oo’ 轴的角动量是否守恒？
o'
α L T
o
F
mg
力矩
o'点 o点 oo'轴
拉力T
0
重力mg
mgLsinα × mgLsinα × 0

大学物理课件：刚体定轴转动的角动量定理 角动量守恒定律

大学物理课件：刚体定轴转动的角动量定理 角动量守恒定律

r
l 2
mv R l mv R l
1
1
2
2
R l
v 2
R
1 v
l 1
2
R
o
l 1
2.刚体的角动量定理及守恒定律
刚体所受合外力矩与角加速度关系为
M J J d
dt
利用角动量表示 M
dJ
dL
dt dt
刚体绕定轴转动时，作用于刚体的合外力矩等于刚 体绕此轴的角动量对时间的变化率。这是刚体角动 量定理的一种形式。
械能守恒。
1 (1 ML2 ma2 ) 2 mga(1 cos60) Mg L (1 cos60)
23
2
3(2ma ML)g 2(3ma2 ML2 )
6(2ma ML)(3ma2 ML2 )
v0
6ma
课后习题 3-9 3-10 3-18
刚体定轴转动的角动量定理 角动量守恒定律
一、冲量矩 角动量
1.冲量矩
定义：力矩与力矩作用时间的乘积称为冲量矩。
数学表达： 2.角动量
t
0 M dt
整个刚体的角动量就是刚体上每一个质元的角动 量——即每个质元的动量对转轴之矩的和。
2.1质点的角动量
v
o
r
m
定义质点 m 相对原点的
角L动 量r定义p为 rmvsin
光滑转轴自由转动。今有一质量为m，速度为v0的子弹， 沿水平方向距水平转轴距离为a射入竖直、静止的杆内。
杆能摆起的最大角度θmax=60°，求v0。 解：把子弹与杆作系统。由于子弹入射杆的瞬间，系统合外力
矩为零故角动量守恒。
设子弹射入后杆起摆的角速度为ω，则有：
m
v0

角动量定理和角动量守恒定律

角动量定理和角动量守恒定律

角动量定理和角动量守恒定律
角动量定理和角动量守恒定律是描述刚体运动时的两个基本定律。

下面进行简单的介绍：
1. 角动量定理
角动量定理是描述角动量变化的定律。

它表示为：物体所受外力矩等于物体角动量对时间的变化率。

即
I*ω= ΔL/Δt
其中，I 为物体的转动惯量，ω为物体的角速度，L 为物体的角动量。

这个定理表明了一个物体的角动量发生变化时，必定受到了外部的力矩作用，即力矩等于角动量的变化率。

2. 角动量守恒定律
角动量守恒定律是描述角动量不变的定律，即如果没有外部力矩作用，系统的总角动量保持不变。

即：
L = L0
其中，L 为系统的总角动量，L0 为系统在某一时刻的总角动量。

这个定律表明，如果没有外部力矩作用，那么系统的总角动量保持不变。

如果一个物体在自由运动时，角动量发生变化，那么它将会改变自身的旋转状态（比如转速、方向等）。

总之，角动量定理和角动量守恒定律是描述刚体运动和角动量变化的基本定理，可以帮助我们更好地理解物体的运动和变化规律。

第5章角动量角动量守恒定律

第5章角动量角动量守恒定律
任一行星和太阳之间的联线,在相等 的时间内扫过的面积相等, 即掠面速 度不变.
(2) 说明天体系统的旋转盘状结构.
v
r
O
B S
A r
[证明]
(1) 行星对太阳O的角动量的大小为 L r p rmvsin
其中 是径矢 r 与行星的动量 p 或速度 v 之间的夹角.
用 s 表示 t 时间内行星所走过的弧长, 则有
dt
若 M外 0
则 dL 0 或 L 常矢量
dt
若对某一固定点，质点所受合外力矩为零， 则质点对
该固定点的角动量矢量保持不变。
例：质点做匀速直线运动中，对0点 角动量是否守恒？
Lo r mv
rmvsin
r mv
L
r
O r
A
p mv
6
例 试利用角动量守恒定律:
1) 证明关于行星运动的开普勒定律:
v1
r1
B S
A
O
r1
积, 如图中所示.
其中 d /dt 称为掠面速度.
由于万有引力是有心力, 它对力心O的力矩总是等于零, 所以角动量守恒, L=常量, 行星作平面运动, 而且
d L 常量
dt 2m
这就证明了掠面速度不变, 也就是开普勒第二定律.
8
(2) 角动量守恒说明天体系统的旋转盘状结构
lim L r ms sin
t0 t
lim L
2m 2m d
t0 t
dt
若用 r 表示从O到速度矢量 v 的垂直距离, 则有
r sin s rs 2
7
lim L
2m 2m d
t0 t
dt
C D
其中 是 t时间内行星 v2

角动量、角动量守恒定律的分析

角动量、角动量守恒定律的分析

02
3
4. 求质量 m ,半径 R 的球体对直径的转动惯量
解：以距中心 r ，厚 dr 的球壳
R
dr
r
为积分元
o
dV 4r 2dr
m
m 4 R3
3
dJ
2 3
dm r 2
2mr 4dr R3
dm dV
J
R
dJ
0
2mr 4dr R3
2 5
mR2
注意： 对同轴的转动惯量才具有可加减性。
直于杆，分别过杆的中点和一端端点的轴的转动惯量。
解：(1) 轴过中点
dm
x
L2
ox
L 2
L
J
r 2dm
m L
1 3
L3 8
L
x2dm
x 2 2
L
L3 8
1 12
2
mL2
m dx L
m L
1 3
x3
2 L
2
(2) 轴过一端端点
dm
o
x
Lx
J r2dm x2dm L x2 mdx 0L m 1 x3 L 1 mL2 L3 0 3
o r m p
p
or
* 质点对某参考点的角动量反映质点绕该参考点旋
转运动的强弱。
*必须指明参考点，角动量才有实际意义。
2. 质点系角动量
L
系i统L内i vr所ii 有i vr质rcci 点 rvp对iii 同 无一有i'：'参：r对i对考参质考点m心点i角vi 动o量r1pr的c1 矢crrp量2ir2i和
i
i
i
式中 J ri2mi
i
刚体对轴的转动惯量

第5讲 角动量定理和角动量守恒定律

第5讲 角动量定理和角动量守恒定律
2）动量守恒与角动量守恒 是相互独立的定律 如行星运动
动量不守恒
角动量守恒
3）向心力： 力始终过某一点。
M 0
o
角动量守恒
F


行星在速度和向心力所组成的平面内运动。
9
例：开普勒第二定律：行星对太阳的径矢在相等的时间
内扫过相等的面积
M 0
dr
L
＝常矢量
L mrsin
方向：垂直 r , F组成的平面
1
M
M
O
z
r
F
*
d
P

确定力矩方向的右手螺旋法则示意图
2
2、质点对定点的角动量
t 时刻 质量m 速度 相对固定o的矢径 r
• 质点动量
p m
为质点对定点o 的角动量
• 定义 L r p
• 大小： r p sin mr sin L
M xi M y j M z k
M x yFz zF y 比较可得： M y zFx xFz M xF yF y x z
M rF x Fx i j y Fy k z Fz
6
3. 质点的角动量定理
Lrp
Lx ypz zp y 比较可得： Ly zp x xp z L xp yp y x z
Lrp x px i j y py k z pz
5
（b）力矩分量
M ( xi yj zk ) ( Fx i Fy j Fz k ) ( yFz zFy )i ( zFx xFz ) j ( xFy yFx )k

大物力学第五章 角动量

大物力学第五章 角动量

v dr v Q =v dt
v v dp F= dt
v dr v v v × p = v × mv = 0 dt
说明： 说明： 可以写成分量表示。 可以写成分量表示。
v dL v v v ∴ = r ×F = M dt
力矩引起角动量的变化！ 力矩引起角动量的变化！
微分形式
v v t2 v L2 − L = ∫ Mdt 1
面积ds=(r·v·dt·sin θ)/2
v r
θ
ds 1 1 v v 面积变化率 = r • v • sin θ = r × v = dt 2 2 2m 角动量守恒 面积变化率恒定
开普勒第二定律
v L
O
v v dt
v v r × v 的含义
面积ds=(r·v·dt·sin θ)/2
v r
θ
ds 1 1 v v 面积变化率 = r • v • sin θ = r × v = dt 2 2 2m 角动量守恒 面积变化率恒定
例：图中O为有心力场的力心，排斥力于距离平方成反 图中 为有心力场的力心， 为有心力场的力心 为一常量） 为一常量 比：f = k/r2（k为一常量） 求：(1) 此力场的势能 (2) 一质量为 的粒子以速度 0、瞄准距离 从远处 一质量为m的粒子以速度 的粒子以速度v 瞄准距离b从远处 入射，求他能达到的最近距离和此时的速度。 入射，求他能达到的最近距离和此时的速度。
v v v Q M内 = ∑ ( ri × f i内 ) i dt i
质点组角动量守恒： 质点组角动量守恒：
矢量，可以写成分量式表示。 矢量，可以写成分量式表示。 只有外力矩才对角动量有贡 内力矩为零， 献，内力矩为零，但会改变角 动量在体系内的分配。 动量在体系内的分配。

§5.1 力矩与角动量(动量矩)

§5.1 力矩与角动量(动量矩)

mM v2 G 2 m R R
例2 已知：在xoy坐标系中，在t=0时刻将质量 为m的质点由a处静止释放，让它自由下落， 求：在任意时刻t，质点所受的对原点o的 力矩？质点对原点o的角动量？ a 1 2 o b x F mgj r bi gt j 解： 2
M r F mgbk P mv mgtj L r P mgbtk
α
l
v m
o
Lo mvl sin , L mvl , o' L oo ' mvl sin ,
r
y
F ( P)
二、矢量对轴的矩
定义：在P点处矢量 B 对z轴的矩为 mz
m z
O
Z
r
P

B
m
B B
B
mz r B sin
0 m rr r O r
对轴的力矩、角动量
Z Z
M
0 r2
O
F2 F
P
P 1
o'
α L
力矩
拉力T
0 TLcosαsinα⊙
重力mg mgLsinα×
mgLsinα×
合力F
FLcosα×
T
o'点
o
F
o点
oo'轴
0
0
mg
0
0
练习2 在图示情况下，已知圆锥摆的质量为m，速 率为v，求圆锥摆对o点,o’点,oo’轴的角动量.
在讨论质点的角动量时，必须指明是对那点或那个轴的角动量 o'
第5章
角动量及其规律
第 5 章 角动量及其规律

角动量变化定理和动量守恒

角动量变化定理和动量守恒
—— 必须指明是对哪个点而言的
2
作圆周运动质点对O点的 角动量 l 的方向垂直于圆周 平面 ，大小为
l mrv mr2
把过O点并垂直于圆周平面的直线当成转轴， 上式表示质点绕该轴转动的角动量。
3
1.5.2 力矩 角冲量和质点角动量变化定理
力矩：M
r
f
方向:用右手螺旋定则判断
大小: M rf sin
4
证明：牛顿定律 角动量定理
f
dp
r
f
r
dp
dt
因
v p 0
r f r
，则有
dp
v
p
dt
r
dt dp
dr
p
d(r
p)
dl
dt dt
dt dt
即
M dl ---微分形式的质点
dt
角动量变化定理 5
M dl dt
质点对惯性系中任一固定点的角动量对时间 的变化率，等于这个质点所受合力对该固定点 的力矩。
12
9
3. 角动量守恒定律
如果质点系d所L受 合0 ，外L力矩常M矢外量 0，则 dt
即，质点系角动量的大小和方向都保持不变。
实验表明： 对于不受外界影响的粒子系统所经历的任意 过程，包括不能用牛顿力学描述的过程，都遵 守角动量守恒定律。
10
盘状星系
11
L
球形原始气云具有初始角动量L，在垂直于L方向， 引力使气云收缩，角动量守恒，粒子旋转速度， 惯性离心力，离心力与引力达到平衡，维持一 定的半径。但在与L平行的方向无此限制，所以 形成了旋转盘状结构。
j( ji )
ri fi
ri fij
j( ji)
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
i i
参考点O，合外力矩 M M i ri Fi i i M - M ri Fi ri Fi i i (ri ri) Fi R Fi
──质点组的角动量守恒定律
§5-1 角动量与力矩
§5-1 角动量与力矩
第 五 章 角动量变化定理与角动量守恒
§5 1 角动量与力矩 §5-1 §5-2 质点组的角动量变化定理 角动量守恒 §5-3 有心运动
1
一.质点的角动量(动量矩)
1.定义：在惯性参考系中选一固 定的参考点O，运动质点对O点的 位矢 r, 动量为 p, 则质点m对O点的 角动量为: L r p r mv
§5-2 质点组的角动量变化定理 角动量守恒
一.质点组的角动量变化定理
1.一对内力的力矩之和为零 如图示,一对内力 fij 和f ji ( fij ) M i M j ri fij rj f ji ( ri rj ) fij
17 18
由于质点所受的力始终指向或背向力心，当质点在初始时 刻的速度v0给定后，质点以后就只能在初速度v0和初始位 矢r所构成的平面内运动，所以，有心力场中质点的运动 必定在一个平面上，是二维的.
3
§5-3 有心运动
§5-3 有心运动
例 试利用角动量守恒定律,证明关于行星运动的开普勒第二 定律：任一行星和太阳之间的联线，在相等的时间内扫过 的面积相等，即掠面速度不变. 证明： 行星对太阳O的角动量 的大小为:
因为一对内力的力矩之和为零, M内 M i内 0 ∴
i
i
i

t2
t1
L2 Mdt dL L2 L1 L
L1
──质点组的角动量变化定理(积分形式) 质点组角动量的增量等于作用于质点组的合外力矩的角冲量.
11 12
2
§5-2 质点组的角动量变化定理 角动量守恒
dL 于是有： M 外 dt
( M 外 和 L 都对同一点)


──质点组的角动量变化定理(微分形式) 质点组所受的合外力矩等于它的角动量对时间的变化率.
式中： M 外 M i外 ri Fi
i
M内 M i内 ri fij i i j i
大小：rmv sin
Z
L
O X
r
Y p mv
m

方向：右手螺旋法则
2
§5-1 角动量与力矩 例:圆运动 匀速圆运动 直线运动 匀速直线运动
§5-1 角动量与力矩 2.角动量的分量表示 L r p r mv
L rmv ⊙ L 常量 L mvd
6
方向：右手螺旋法则
--- F 对O点 的力臂


5
1
§5-1 角动量与力矩
§5-1 角动量与力矩 注意:力矩和角动量都是对于惯性系中同一点.
三.质点的角动量变化定理
由
d dp M r F 和 F ( mv ) dt dt dp d dr r p p M r dt d t dt dr dr v p v mv 0 dt dt d dL dL Mdt M (r p) dt dt —角动量变化定理 (微分形式)
§5-2 质点组的角动量变化定理 角动量守恒
二.质点组的角动量守恒定律
1.质点组的角动量守恒条件 由质点系的角动量定理, 若对于某点 某点而言,质点系所受的 外力矩之和为零, 则质点系对该点 该点的角动量（动量矩）不 随时间改变, 即：
若 M外 0 ,则 L C
2.合外力为零时合外力矩与参考点无关 参考点O，合外力矩： M M i ri Fi
若用 r表示从O到速度矢 量 v 的垂直距离，则有 r sin r
dS
1 r sin v dt 2 dS dt
其中dS /dt 称为掠面速度.
L r m v sin 2m
L = r p r m v sin
其中 是径矢 r与行星的动量 p或速度 v 之间的夹角.
R Fi
i
i
当 Fi 0
i
i
m2 r1 r1 r2 r2 r3 O m3 R r O 3 F3
M M
m1
F1 F2
13
合外力为零时合外力矩与参考点无关.
14
§5-2 质点组的角动量变化定理 角动量守恒
§5-3 有心运动
A
一对内力的角冲量之和为零.
9 10
§5-2 质点组的角动量变化定理 角动量守恒
§5-2 质点组的角动量变化定理 角动量守恒
2.质点组的角动量变化定理 质点组角动量： L Li (对同一点) i dLi dL d （ L） i dt dt i dt i （M i外 M i内） M 外 M内
例:如图, 理想轻滑轮, 轻绳, m1 = m2, 从静止开始, 问哪个猴先到? 解: m1, m2系统合外力矩为零， 对O角动量守恒. 设右边绳对地速度为V, 方向向上.
R1m1O NhomakorabeaT1
T2
§5-3 有心运动
一.质点在有心力场中的运动方程
1. 有心力
2 m1 m2
m2 m1g m2g
有心力:方向始终指向或背向一个固定中心的力 有心力场:有心力存在的空间
L 常量
⊙
v m O r
r
在直角坐标系中： L Lx i Ly j Lz k
Lx yp z zp y ymvz zmv y

v
Ly zpx xpz zmvx xmvz
p 不变 L 不变
L 不变, p 不一定不变
0 M i dt M j dt 0
mω0 r02 m r 2 v r 0 r02 r
由动能定理，有
0
r0
r
Fi
mi

r﹣ i rj fji
v0 F0
ri
O
fij

mj
Fj
rj
2 1 2 1 2 1 2 2r mv mv0 m0 r0 02 1 2 r 2 2 3 r0 2 2 当r 时，拉力的功为: A m0 r0 2 2
大小： r F sin F d
M
在直角坐标系中：M M x i M y j M z k
M x yFz zFy
O
d r
P
M y zFx xFz M z xFy yFx i M Mx,M y,Mz x Fx j y Fy k z Fz
(中心对称)有心力：有心力的大小仅与参考点P到力心O的
, 2 为m1,m2对绳的速度，有 1
V )R 0 m1 (1 V ) R m2 (2 ) 2 解得 V (1 2 ) 2 1 2 (1 2
15
距离r 有关，即 F = F ( r ) er 可以证明，这类有心力必定是保守力.

t2
t1
L2 Mdt dL L2 L1 L —角动量变化定理(积分形式)
L1
四.质点的角动量守恒定律
当 M 0 时，L 常量
若质点所受的合力矩为零, 则质点的角动量不随时间改变.
M r F
7
质点所受的合外力矩的冲量矩等于它的角动量增量-质点角动量变化定理
16
§5-3 有心运动
§5-3 有心运动
2.运动方程 在有心力场中运动的质量为m的质点，其运动方程为 mr F ( r ) er
3. 二维平面运动与运动方程
二.角动量守恒和机械能守恒
有心力场中运动的质点的特点: 角动量守恒： 由于有心力对力心O的力矩为零，所以在有心力场中运 动的质点对力心O的角动量守恒. 机械能守恒： 由于有心力是保守力，所以在有心力场中运动的质点的 机械能也守恒.
O
d
m
Lz xp y ypx xmv y ymvx
3
i L Lx , Ly , Lz x px


j y py
k z pz
4
§5-1 角动量与力矩
§5-1 角动量与力矩 2.力矩的分量表示 M rF F
二.力矩
1.定义： M rF
M 0
F 0 F 过 O点
8
§5-1 角动量与力矩 例:小球质量为m.先使小球以角速度0绕管心作半径为r0的圆 周运动，然后向下拉绳子. 求:将小球拉至离中心r0/2处时，拉力 F0所作的功. 解:小球在有心力作用下运动: L 常量 L mvr m r 2
O
§5-2 质点组的角动量变化定理 角动量守恒
19
由于万有引力是有心力，它对力心O的力矩总是等于零， 所以角动量守恒 L 常量



即
dS L 常量 dt 2 m
——开普勒第二定律
20
4