下载文档原格式
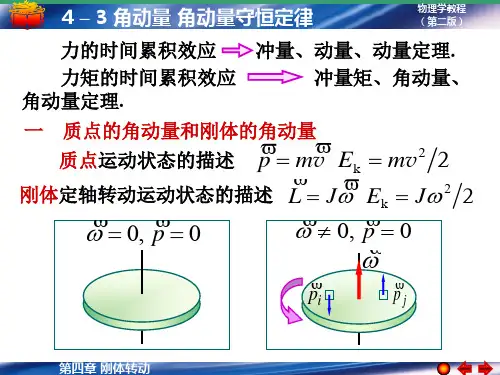
力矩的时间累积效应刚体的角动量定理力矩是一个非常重要的概念，在物理学中有广泛的应用。
力矩是由施加在刚体上的力产生的，它对物体的角动量有直接的影响。
力矩的大小等于力在垂直于力的作用线上的距离与力的大小的乘积。
力矩既可以使物体转动，也可以改变物体的转动状态。
刚体的角动量定理描述了外力对刚体的角动量产生的影响。
角动量定理可以表示为：\[\frac{{\Delta L}}{{\Delta t}} = M_n\]其中，ΔL是物体在时间Δt内的角动量的变化，M_n是刚体的合外力矩。
这个方程说明了外力对刚体角动量的改变率是力矩。
角动量定理的解释是，当一个刚体受到一个力矩的作用时，其角动量将发生改变。
外力矩是由施加在物体上的所有力矩之和。
外力矩可以通过计算所有作用力的力矩之和得到。
外力矩越大，刚体的角动量变化越大。
重要的是要注意，这个角动量定理适用于刚体。
对于质点来说，可以将刚体看作是一个质点，并将其质量集中在一个点上。
因此，对于质点，角动量定理也适用。
力矩的时间累积效应是指力矩对刚体角动量的积累作用。
当外力施加在刚体上一段时间后，会导致角动量的累积变化。
这是因为力矩在一段时间内对刚体的作用会积累产生更大的角动量变化。
例如，我们将一根悬挂在一个轴上的刚体上施加一个力。
在一段时间内，力矩将会产生一个初始的角动量，并且随着时间的推移，角动量将不断积累。
这是因为力矩在每个时间间隔内的作用都会增加角动量的变化。
力矩的时间累积效应还可以通过另一个实例来说明。
考虑一个旋转的滚筒，在初始时刻没有任何外力矩作用在上面。
当我们施加一个外力矩时，滚筒将开始旋转。
如果我们保持外力矩的大小和方向不变，滚筒将继续旋转。
然而，如果我们改变外力矩的大小或方向，滚筒的角动量将发生变化。
角动量的变化是根据力矩的改变率来计算的。
这意味着力矩的时间累积效应将导致角动量的变化。
进一步分析力矩的时间累积效应，我们需要考虑刚体的质量分布和外力的作用时间。
