下载文档原格式
时序逻辑电路课后习题答案时序逻辑电路课后习题答案时序逻辑电路是数字电路中的一种重要类型，它在数字系统中起到了关键的作用。
通过时序逻辑电路，我们可以实现各种复杂的功能，例如计数器、寄存器、状态机等。
然而，在学习过程中，我们常常会遇到一些难题，下面我将为大家提供一些常见时序逻辑电路习题的答案，希望能够对大家的学习有所帮助。
1. 设计一个4位二进制计数器，要求计数范围为0-9，采用时序逻辑电路实现。
答案：这是一个常见的计数器设计问题。
我们可以使用四个触发器构成一个4位二进制计数器。
每个触发器的输出作为下一个触发器的时钟输入，形成级联结构。
每当计数器的值达到9时，我们需要将其清零，即将四个触发器的输入端都置为0。
这样，当计数器的值达到9时，下一个时钟脉冲到来时，触发器的输出将变为0，实现了计数器的循环。
2. 设计一个状态机，实现一个简单的交通信号灯系统。
红灯亮20秒，绿灯亮30秒，黄灯亮5秒，然后再次循环。
答案：这是一个典型的状态机设计问题。
我们可以使用两个触发器来实现该状态机。
首先，我们需要定义三个状态：红灯状态、绿灯状态和黄灯状态。
然后，我们可以使用一个计数器来计时。
当计时达到20秒时，状态机切换到绿灯状态；当计时达到50秒时，状态机切换到黄灯状态；当计时达到55秒时，状态机切换到红灯状态。
然后，状态机重新开始计时，循环执行上述过程。
3. 设计一个电梯控制系统，实现电梯的上升和下降功能，并能够响应乘客的楼层请求。
答案：电梯控制系统是一个较为复杂的时序逻辑电路设计问题。
我们可以使用一个状态机来实现该系统。
首先，我们需要定义电梯的各个状态，例如静止状态、上升状态和下降状态。
然后，我们可以使用一个计时器来计时，以确定电梯的运行时间。
当电梯处于静止状态时，它可以响应乘客的楼层请求，并根据请求的楼层决定是上升还是下降。
当电梯到达目标楼层时，它会停止运行并等待下一个请求。
当电梯处于上升或下降状态时，它会根据当前楼层和目标楼层的差值来确定运行方向，并在到达目标楼层后停止运行。
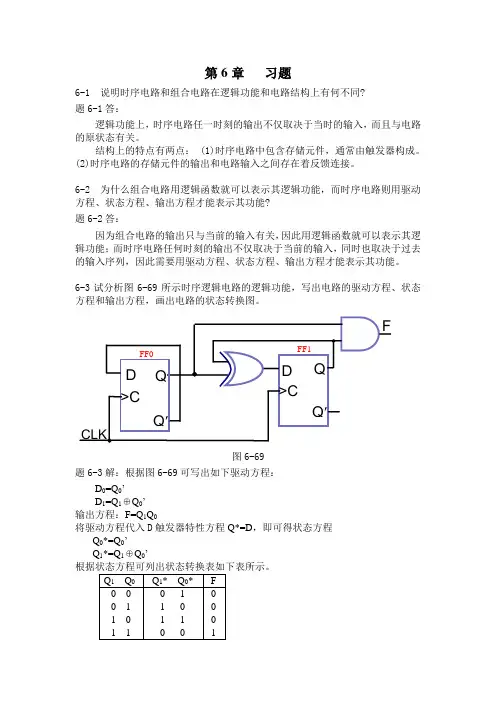
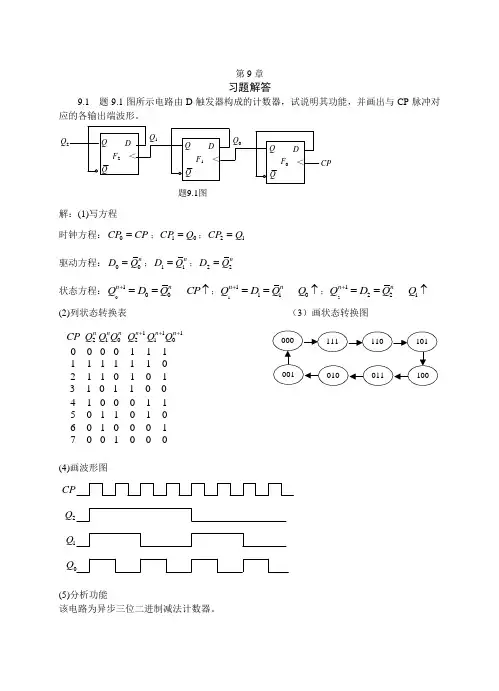
第9章习题解答9.1 题9.1图所示电路由D 触发器构成的计数器，试说明其功能，并画出与CP 脉冲对应的各输出端波形。
Q CP题9.1图解：(1)写方程时钟方程：0CP CP =；10CPQ =；21CP Q = 驱动方程：00n D Q =；11n D Q =；22n D Q =状态方程：0100n n Q D Q CP +==↑；11110n n Q D Q Q +==↑；21221n nQ D Q Q +==↑(2)列状态转换表 （3）画状态转换图111210210n n n n n n CP Q Q Q Q Q Q +++0 0 0 0 1 1 11 1 1 1 1 1 02 1 1 0 1 0 13 1 0 1 1 0 04 1 0 0 0 1 15 0 1 1 0 1 06 0 1 0 0 0 17 0 0 1 0 0 0(4)画波形图CP 2Q 1Q 0Q(5)分析功能该电路为异步三位二进制减法计数器。
9.6 已知题9.6图电路中时钟脉冲CP 的频率为1MHz 。
假设触发器初状态均为0，试分析电路的逻辑功能，画出Q 1、Q 2、Q 3的波形图，输出端Z 波形的频率是多少？CP题9.6图解：(1)写方程时钟方程：123CP CP CP CP ===驱动方程：113n n D Q Q =；212n n D Q Q =⊕；312n n D Q Q =状态方程：11113n n n Q D Q Q CP +==↑;12212n n n Q D Q Q CP +==⊕↑;13312n n n Q D Q Q CP +==↑ 输出方程：3n Z Q =(2)列状态转换表 （3）画状态转换图111321321n n n n n n CP Q Q Q QQ Q Z+++0 0 0 0 0 0 1 01 0 0 1 0 1 0 02 0 1 0 0 1 1 03 0 1 1 1 0 0 04 1 0 0 0 0 0 1 1 0 1 0 1 0 1 1 1 0 0 1 0 1 1 1 0 0 1 0 1(4)画波形图(5)分析功能该电路为能够自启动的同步5进制加法计数器。
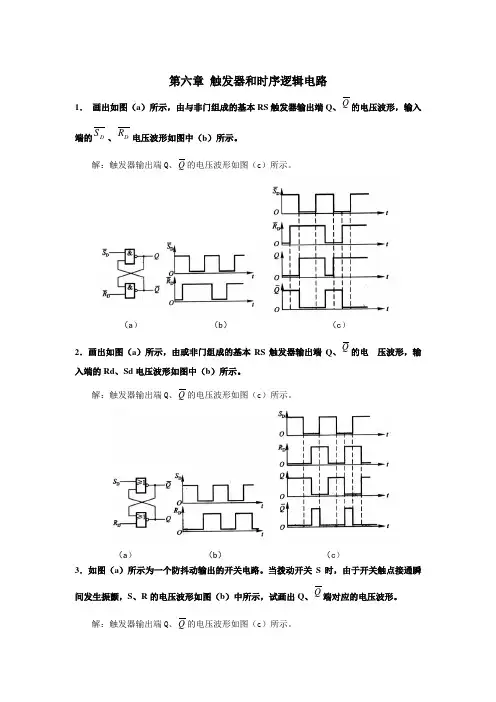
（a ）（b ）（c ）（a ）（b ）（c ）第六章 触发器和时序逻辑电路1． 画出如图（a ）所示，由与非门组成的基本RS 触发器输出端Q 、Q 的电压波形，输入端的D S 、D R 电压波形如图中（b ）所示。
解：触发器输出端Q 、Q 的电压波形如图（c ）所示。
2．画出如图（a ）所示，由或非门组成的基本RS 触发器输出端Q 、Q 的电 压波形，输入端的Rd 、Sd 电压波形如图中（b ）所示。
解：触发器输出端Q 、Q 的电压波形如图（c ）所示。
3．如图（a ）所示为一个防抖动输出的开关电路。
当拨动开关S 时，由于开关触点接通瞬间发生振颤，S 、R 的电压波形如图（b ）中所示，试画出Q 、Q 端对应的电压波形。
解：触发器输出端Q 、Q 的电压波形如图（c ）所示。
（a） （b ）（c ）（a ） （b ）4．图（a ）所示的各触发器初始状态Q 都为0，画出在CP 信号作用下，各触发器输出端的电压波形。
（a ）（b ）（a ）（b ）（a ）（b ）解：各触发器输出端的电压波形如图（b ）所示。
5．在图（a ）所示电路中，画出在图（b ）的D 、CP 作用下Q0、Q1的波形。
设触发器初始状态都为0。
解：由图可得01D Q n =+ nn n n n Q Q Q K Q J Q 101111=+=+作如图（b ）所示的波形。
6．如图（a ）所示电路中，画出在图（b ）D 、CP 作用下Q1、Q2的波形。
设触发器初始状态都为0。
解：由图可得D Q n =+11nn n n n n Q Q Q Q Q Q 1212112=+=+作如图（b ）所示的波形。
7． 分析图（a ）时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图，说明电路能否自启动。
（a ）（b ）解：驱动方程：状态方程：输出方程：电路能自启动，状态转换图如图（b ）所示。
8．试分析图（a ）时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图。
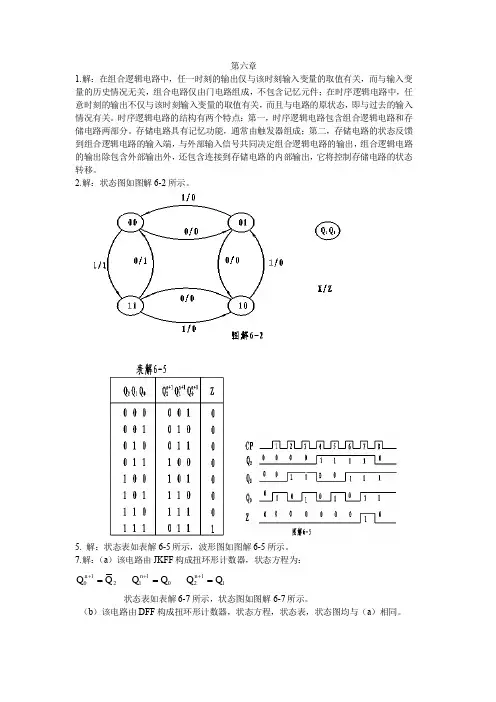
第6章时序逻辑电路6—1 从概念，结构和功能描述等几个方面简述时序逻辑电路和组合逻辑电路的不同。
概念：组合逻辑电路在任一时刻的输出仅由该时刻的输入决定，而与过去的状态无关，电路无记忆功能。
时序逻辑电路任一时刻的输出信号不仅取决于该时刻的输入信号，而且还取决于电路原来的状态。
结构：组合电路都是单纯由逻辑门组成，且输出不存在反馈路径。
时序逻辑电路由组合逻辑电路和存储电路组成，输出和输入之间有反馈。
存储电路一般由触发器构成。
功能描述：组合逻辑电路一般用逻辑图、逻辑表达式和真值表描述。
时序逻辑一般用逻辑图、逻辑方程式（状态方程、输出方程、驱动方程）、状态转换表、状态转换图和时序图来描述。
6—2 作出与表1所示状态表对应的状态图。
6—3 用边沿触发D触发器和与非门设计一个三位右移寄存器，用一控制端X控制，当0=X时能串行输入新数据ID，当1=X时具有自循环功能。
A BD C2111/10X/010/011/010/001/101/010/011/000/001/1QQSETCLRDQQSETCLRDQQSETCLRDXD ID OCP6—4 完成下列设计：1. 画出用J-K 触发器实现的四位右移寄存器的逻辑图（数据向高位移位定义为右移，寄存器的输出1Q 2Q 3Q 4Q ，设4Q 为高位。
2. 用上述四位右移寄存器实现下列计数器，写出设计步骤，画出逻辑图。
CP 1Q 2Q 3Q 4Q0 0 0 0 0 11 0 0 02 0 1 0 0 31 0 1 0 4 0 1 0 1 5 0 0 1 0 6 0 0 0 1 70 0 0 0答：由题意知，计数器是由右移寄存器实现的，所以只要确定第一个JK 触发器的驱动方程即可。
根据给出的状态转换表，可得卡诺图。
化简得43Q Q Q Q Q Q D ++=⋅⋅=6—5 用一片74LS161和必要的门电路构成一个可控计数器。
当控制端C=1时，实现八进制计数；C=0时，实现四进制数。
第六章时序逻辑电路6.1 基本要求1. 正确理解组合逻辑电路、时序逻辑电路、寄存器、计数器、同步和异步、计数和分频等概念。
2. 掌握时序逻辑电路的分析方法，包括同步时序逻辑电路和异步时序逻辑电路。
3. 熟悉寄存器的工作原理、逻辑功能和使用。
4. 掌握二进制、十进制计数器的构成原理。
能熟练应用集成计数器构成任意进制计数器。
5. 掌握同步时序逻辑电路的设计方法。
6.2自测题一、填空题1．数字电路按照是否有记忆功能通常可分为两类：、。
2．由四位移位寄存器构成的顺序脉冲发生器可产生个顺序脉冲。
3．时序逻辑电路按照其触发器是否有统一的时钟控制分为时序电路和时序电路。
4. 用D触发器来构成12进制计数器，需要个D触发器。
二、选择题1．同步计数器和异步计数器比较，同步计数器的显著优点是。
A.工作速度高B.触发器利用率高C.电路简单D.不受时钟CP控制。
2．把一个五进制计数器与一个四进制计数器串联可得到进制计数器。
A.4B.5C.9D.203. N个触发器可以构成最大计数长度（进制数）为的计数器。
A.NB.2NC.N2D.2N4. N个触发器可以构成能寄存位二进制数码的寄存器。
A.N-1B.NC.N+1D.2N5．五个D触发器构成环形计数器，其计数长度为。
A.5B.10C.25D.326．同步时序电路和异步时序电路比较，其差异在于后者。
A.没有触发器B.没有统一的时钟脉冲控制C.没有稳定状态D.输出只与内部状态有关7．一位8421BCD码计数器至少需要个触发器。
A.3B.4C.5D.108.欲设计0，1，2，3，4，5，6，7这几个数的计数器，如果设计合理，采用同步二进制计数器，最少应使用级触发器。
A.2B.3C.4D.89．8位移位寄存器，串行输入时经个脉冲后，8位数码全部移入寄存器中。
A.1B.2C.4D.810．用二进制异步计数器从0做加法，计到十进制数178，则最少需要个触发器。
A.2B.6C.7D.8E.1011．某电视机水平-垂直扫描发生器需要一个分频器将31500H Z的脉冲转换为60H Z的脉冲，欲构成此分频器至少需要个触发器。
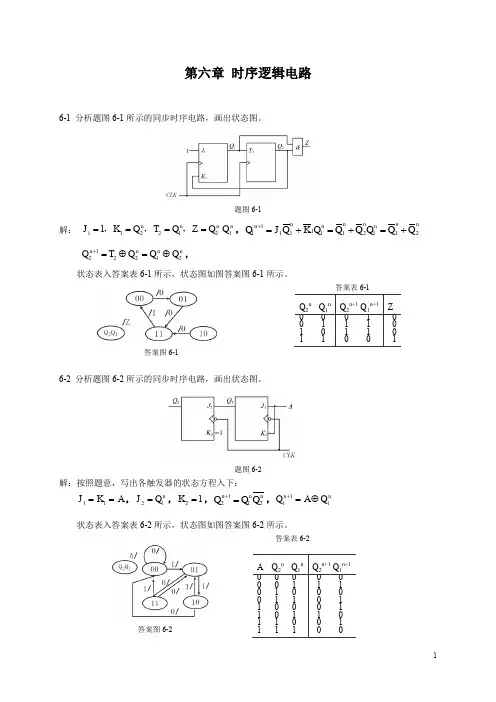
第六章 时序逻辑电路6-1 分析题图6-1所示的同步时序电路，画出状态图。
题图6-1解： 11221211n n n n J K Q T Q Z Q Q ====，，，，11111111212n n n n nn n nQ J Q K Q Q Q Q Q Q +=+=+=+122212n n n n Q T Q Q Q +=⊕=⊕，状态表入答案表6-1所示，状态图如图答案图6-1所示。
答案表6-1答案图6-16-2 分析题图6-2所示的同步时序电路，画出状态图。
题图6-2 解：按照题意，写出各触发器的状态方程入下：11J K A ==，21n J Q =，21K =，1212n n nQ Q Q +=，111n n Q A Q +=⊕状态表入答案表6-2所示，状态图如图答案图6-2所示。
答案表6-2答案图6-2Q 2n Q 1n Q 2n+1 Q 1n+1 Z0 0 0 1 1 0 1 1 0 1 1 1 1 1 0 0 0 0 0 1A Q 2n Q 1n Q 2n+1 Q 1n+1 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 0 1 1 0 0 0 1 0 1 1 0 0 1 0 0CLK D 1D 2D 3Q 3Q 2Q 1Q 2Q 3Q 1Q 1Q 2Q 3&6-3分析题图6-3所示的同步时序电路，画出状态图。
题图6-3解：按照题意，写出各触发器的状态方程入下：1112213232131n n n nn J K T J K Q Q T J Q Q K Q ========1，，， 133********n n n n n n n nQ J Q K Q Q Q Q Q Q +=+=+ 1222132n n n n nQ T Q Q Q Q +=⊕=⊕ 1111111n n n n Q T Q Q Q +=⊕=⊕=答案表6-3答案图6-36-4 在题图6-4所示的电路中，已知寄存器的初始状态Q 1Q 2Q 3=111。
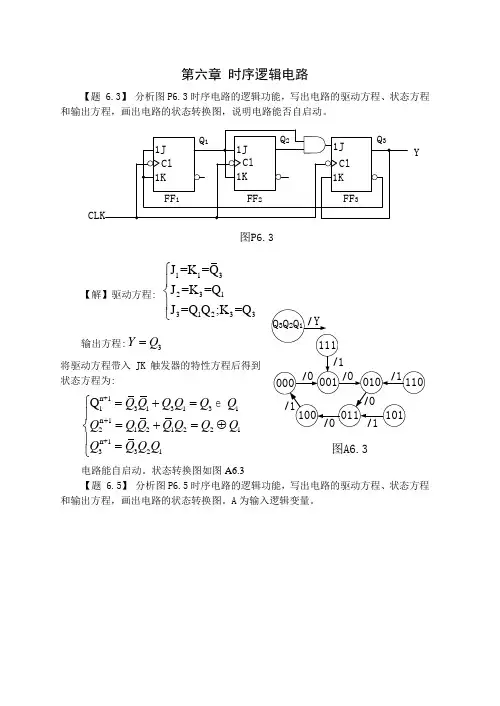
第六章 时序逻辑电路【题 6.3】 分析图P6.3时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图，说明电路能否自启动。
Y图P6.3【解】驱动方程:11323131233J =K =Q J =K =Q J =Q Q ;K =Q ⎧⎪⎨⎪⎩ 输出方程:3YQ =将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+11313131n 12121221n+13321Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q +⎧=+=⎪=+=⊕⎨⎪=⎩ 电路能自启动。
状态转换图如图A6.3【题 6.5】 分析图P6.5时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图。
A 为输入逻辑变量。
图A6.3Y图P6.5【解】驱动方程: 1221212()D AQ D AQ Q A Q Q ⎧=⎪⎨==+⎪⎩输出方程: 21Y AQ Q =将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+112n+1212()Q AQ QA Q Q ⎧=⎪⎨=+⎪⎩ 电路的状态转换图如图A6.51图A6.5【题 6.6】 分析图P6.6时序电路的逻辑功能，画出电路的状态转换图，检查电路能否自启动，说明电路能否自启动。
说明电路实现的功能。
A 为输入变量。
AY图P6.6【解】驱动方程: 112211J K J K A Q ==⎧⎨==⊕⎩输出方程: 1212Y AQ Q AQ Q =+将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+111n+1212QQ Q A Q Q ⎧=⎪⎨=⊕⊕⎪⎩ 电路状态转换图如图A6.6。
A ＝0时作二进制加法计数，A ＝1时作二进制减法计数。
01图A6.6【题 6.7】 分析图P6.7时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图，说明电路能否自启动。
Y图P6.7【解】驱动方程: 001023102032013012301;;;J K J Q Q Q K Q J Q Q K Q Q J Q Q Q K Q==⎧⎪=∙=⎪⎨==⎪⎪==⎩ 输出方程: 0123Y Q Q Q Q =将驱动方程带入JK 触发器的特性方程后得到状态方程为:*00*1012301*2023012*3012303()Q ()Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q⎧=⎪=++⎪⎨=++⎪⎪=+⎩ 设初态Q 1Q 3Q 2Q 1 Q 0=0000，由状态方程可得：状态转换图如图A6.7。
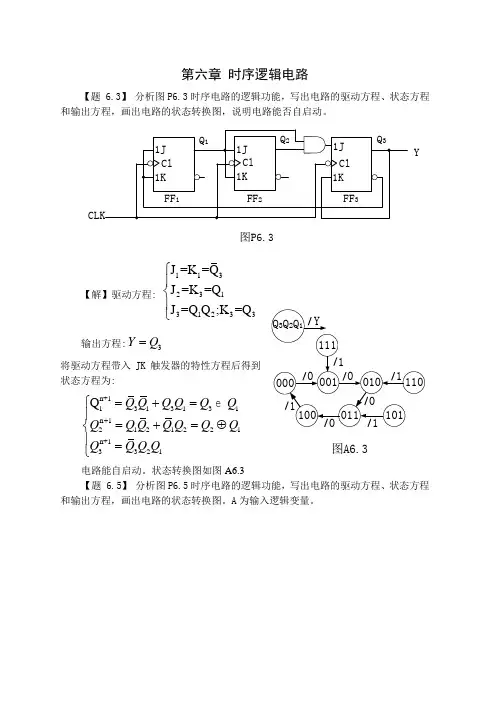
第六章 时序逻辑电路【题 6.3】 分析图P6.3时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图，说明电路能否自启动。
Y图P6.3【解】驱动方程:11323131233J =K =Q J =K =Q J =Q Q ;K =Q ⎧⎪⎨⎪⎩ 输出方程:3YQ =将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+11313131n 12121221n+13321Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q +⎧=+=⎪=+=⊕⎨⎪=⎩ 电路能自启动。
状态转换图如图A6.3【题 6.5】 分析图P6.5时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图。
A 为输入逻辑变量。
图A6.3Y图P6.5【解】驱动方程: 1221212()D AQ D AQ Q A Q Q ⎧=⎪⎨==+⎪⎩输出方程: 21Y AQ Q =将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+112n+1212()Q AQ QA Q Q ⎧=⎪⎨=+⎪⎩ 电路的状态转换图如图A6.51图A6.5【题 6.6】 分析图P6.6时序电路的逻辑功能，画出电路的状态转换图，检查电路能否自启动，说明电路能否自启动。
说明电路实现的功能。
A 为输入变量。
AY图P6.6【解】驱动方程: 112211J K J K A Q ==⎧⎨==⊕⎩输出方程: 1212Y AQ Q AQ Q =+将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+111n+1212QQ Q A Q Q ⎧=⎪⎨=⊕⊕⎪⎩ 电路状态转换图如图A6.6。
A ＝0时作二进制加法计数，A ＝1时作二进制减法计数。
01图A6.6【题 6.7】 分析图P6.7时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图，说明电路能否自启动。
Y图P6.7【解】驱动方程: 001023102032013012301;;;J K J Q Q Q K Q J Q Q K Q Q J Q Q Q K Q==⎧⎪=∙=⎪⎨==⎪⎪==⎩ 输出方程: 0123Y Q Q Q Q =将驱动方程带入JK 触发器的特性方程后得到状态方程为:*00*1012301*2023012*3012303()Q ()Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q⎧=⎪=++⎪⎨=++⎪⎪=+⎩ 设初态Q 1Q 3Q 2Q 1 Q 0=0000，由状态方程可得：状态转换图如图A6.7。
第六章时序逻辑电路【题6.3】 分析图P6.3时序电路的逻辑功能，写出电路的驱动方程、状态方程 和输出方程，画出电路的状态转换图，说明电路能否自启动。
图 P6.3【解】驱动方程J-] =K 1=Q 3*」2=心二Q i输出方程：Y -Q 3将驱动方程带入 JK 触发器的特性方程后得到 状态方程为：Q 1= Q 3Q*I + Q 3Q 〔 = Q D'Q 2 = Q 〔Q 2 + Q 〔Q 2 = Q 2 ㊀ n+1 — Q3- Q 3Q 2Q i电路能自启动。
状态转换图如图 A6.3和输出方程，画出电路的状态转换图。
A 为输入逻辑变量。
【题6.5】 分析图P6.5时序电路的逻辑功能, 写出电路的驱动方程、 状态方程J3= Q 1Q 2；K3= Q图P6.5【解】口=AQ2驱动方程：D2=AQQ =AQ +Q2)输出方程：Y将驱动方程带入JK触发器的特性方程后得到状态方程为Q n+1=A&2n+1Q；=A(Q i Q2)电路的状态转换图如图A6.5图A6.5【题6.6】分析图P6.6时序电路的逻辑功能，画出电路的状态转换图，检查电路能否自启动，说明电路能否自启动。
说明电路实现的功能。
A为输入变量。
【解】驱动方程输出方程：丫二AQQ2-A QQ2将驱动方程带入JK触发器的特性方程后得到状态方程为：Q n+1 = Q rn+1 - -Q2二A 二Q r二Q2电路状态转换图如图A6.6。
A = 0时作二进制加法计数，A = 1时作二进制减法计数。
图A6.6【题6.7】分析图P6.7时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图，说明电路能否自启动。
J o = © = 1J1 = Q 0 * Q2 Q 3; K1 = Q oJ 2 =Q o Q 3；K 2 =QoQJ3 = Q0QQ 2； K 3 = Qo输出方程：丫二Q 0QQ 2Q 3将驱动方程带入JK 触发器的特性方程后得到状态方程为Q o =QoQ ；二 Q O Q Q Q 3) Q 0Q 1Q 2 = Q o QQ 3 ' (Q o Q 1)Q 2设初态Q 1Q 3Q 2Q 1 Q o =OOOO ，由状态方程可得:1图 P6.7Y【解】驱动方程数字电子技术基础参考答案 第五章状态转换表初态次态输出**** 栋**Q Q Q Q Q Q QQ PY 0 0 0 0： 10 0 1 1 0 0 0 1 0 0 0 0 0 0 0 10 0 0 0 1 0 0 0 11 0 0 10 0 0 10 0 0 0 11 0 0 10 1 0 10 0 0 0 110 0 10 1 0 0 111 0 110 0 10 0 0 0 111 0 10 0 1 10 0 0 0 10 10 0 10 1 0 10 11 10 10 0 110 0 0 0 11 0 110 1 110 0 0 1110 0 10 1 0 11111110状态转换图如图 A6.7。
电路能自启动图 A6.7【题6.9】试画出用4片74LS194组成16位双向移位寄存器的逻辑图。
的功能表见表 632 。
【解】见图A6.900000011/074LS19411001Q 3C 2QIQ 0丫.0111」0 0 01010 1010 -4—1100 *—<_7/0数字电子技术基础参考答案第五章出输行串入输行串移左d o96A 图出 +移输 P 左行D u 4y x S 0/o氏& BA入输行串入输据数行并【题6.10】在图P6.10电路中，若两个移位寄存器中的原是数据分别为A3A2A1A O=1001, B 3B2B1B0=0011，试问经过4个CLK信号作用以后两个寄存器中数据如何？这个电路完成什么功能？图P6.10【解】经过4个时钟信号后，两个寄存器里的数据分别为A3A2A1A0= 1100 ,B3B2B1B0=0000。
这是一个4位串行加法器电路。
CL的初始值设为0。
【题6.11】在图P6.11计数器电路，说明这是多少进制的计数器。
十进制计数器74160的功能表见表6.3.4。
图P6.11【解】图P6.11电路为七进制计数器。
【题6.12】在图P6.12计数器电路，画出电路的状态转换图，说明这是多少进制的计数器。
十六进制计数器74LS161的功能表6.3.4所示图 P6.12【解】电路的状态转换图如图 C A6.12。
这是一个十进制计数器。
【题 6.10】试用4位同步二进制计数器74LS161接成十二进制计数器，标出输 入、输出端。
可以附加必要的门电路。
74LS161的功能表见表 6.3.4【解】见图A6.10Y 进位输出Y进位输出图A5.10【题6.13】试分析图P6.11的计数器在M= 1和W 0时各为几进制。
74160 的功能表见表634 。
进位输出1图A6.13>CLK【解】M= 1时为六进制计数器，M= 0时为八进制计数器。
【题6.15】图P6.15电路时可变进制计数器。
试分析当控制变量A为电路各为几进制计数器。
74LS161的功能表见表6.3.4 。
图P6.15【解】A= 1时为十二进制计数器，A= 0时为十进制计数器。
【题6.16】设计一个可控进制的计数器，当输入控制变量W 0时工作在五进制, M=时工作在十五进制。
请标出计数输入端和进位输出端。
【解】见图A6.16。
【题6.17】分析图C P6.17给出的计数器电路，画出电路的状态转换图，说明这是几进制计数器。
74LS290的电路见图6.3.31。
图 P6 17进位输出Q 3Q 2QQ 0的0110、0111、1110、1111四个状态为过渡状态。
图 A6.1774LS161的功能表见表 6.3.4。
【解】这是一个七进制计数器。
电路的状态转换图如图A6.17所示。
其中【题6.18】试分析图 P6.18计数器电路的分频比（即 Y 与CLK 的频率之比）图P6.18【解】第（1 ）级74LS161接成了七进制计数器，第（2）级74LS161接成了九进制计数器，两级串接7 9 = 63进制计数器。
故Y的频率与CLK的频率之比为1 : 63。
【题6.19】图P6.19电路是由两片同步十进制计数器74160组成的计数器，试分析这是多少进制的计数器，两片之间是几进制。
74160的功能表见表6.3.4。
图P6.19【解】第（1）片74160接成十进制计数器，第（2）片74160接成了三进制计数器。
第（1）片到第（2）片之间为十进制，两片串接组成三十进制计数器。
【题6.20】分析图P6.20给出的电路，说明这是多少进制的计数器，两片之间是多少进制。
74LS161的功能表见表6.3.4 。
图P6.20【解】在出现LD = 0信号以前，两片 74LS161均按十六进制计数。
即第（1）片到第⑵片为十六进制。
当第（1）片计为2，第（2）片计为5时产生LD = 0信号，总 的进制为5 16+ 2 + 1= 83故为八十三进制计数器。
【题6.22】用同步十进制计数器芯片74160设计一个三百六十五进制的计数器。
要求各位间为十进制关系。
允许附加必要的门电路。
74160的功能表见表6.3.4。
【解】见图A6.22图 A6.22【题6.23】设计一个数字钟电路， 要求能用七段数码管显示从 0时0分0秒到23时 59分59秒之间的任一时刻。
【解】电路接法可如图 A6.23所示。
计数器由六片 74160组成。
第（1）、（ 2）两片接 成六十进制的“秒计数器”，第（1）片为十进制，第（2）片为六进制。
第（3）、（ 4） 片为接成六十进制的“分计数器”，接法与“秒计数器”相同。
第（5）、第（6）片用 整体复位法接成二十四进制计数器，作为“时计数器”。
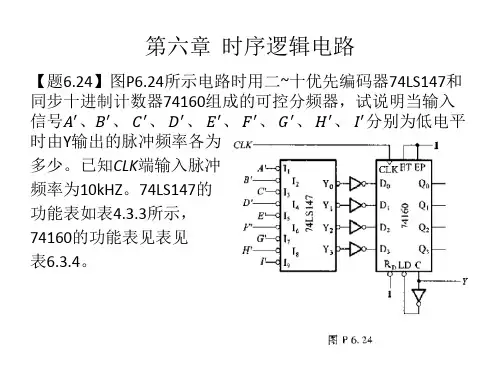
显示译码器由六片 7448组成，每片7448用于驱动一只共阴极的数码管BS201A个位CLK计数 输入Y 进位 输出十位百位LD ) D 1 D 2 D 3 EP CLK Q Q Q QC —LD^_ET 74160(1)ET 74160(2)ET74160(3)>CLK Q Q Q QE P D 0 Di D 2 D 3 CLD>CLK Q Q Q Q REp D 0 D D 2 O C LDFnr~y匚口4-聖W X Ms rl 冷殳0目AU -口<7宰■ ^― — ^― ^― --------------------------------- ---------------- —IrBS 第史◎: n@s g寸£d u es ^i口 u : H I I fs曽r lAnH冒TXTtw 居££00V琨【题6.24】图P6.24所示电路是用二一一十进制优先编码器 74LS147和同步十进制 计数器74160组成的可控分频器，试说明当输入控制信号 A 、B 、C D 、E 、F 、G H 、 I 分别为低电平时由 Y 端输出的脉冲频率各为多少。
已知CP 端输入脉冲的频率为IOKH N 74LS147的功能表如表433所示，74160的功能表见表6.3.4。
图 P6.24【解】由图可见，计数器 74160工作在可预置数状态，每当计数器的进位输出时（即Q 3Q 2QQ 0 = 1001时），在下一个CP 上升沿到达时置入编码器 74LS147的输出 状态 Y 3Y 2 Y 1 Y 0.图 A6.24再从图A6.24给出的74160的状态转换图可知，当A = 0时74LS147的输出为 =1110, 74160的数据输入端 D 3D 2 D 1 D 0 =0001，则状态转换顺序将如图中所示， 即成为九进制计数器。
输出脉冲Y 的频率为CLK 频率的1/9。
依次类推便可得到下表：CLK — A _o| B —o C _O D —o E Y F ―□ G YI 1 I 2 13 I 4丨5丨617I 8 IY 0 Y 1 c H>— CP ET D )EPY 2D 2R D LD CC =1【题6.25】试用同步十进制可逆计数器 74LS190和二一一十进制优先编码器74LS147设计一个工作在减法计数器状态的可控分频器。
要求在控制信号 A 、B 、C DE 、F 、GH 分别为 1 试分频比对应为 1/2、1/3、1/4、1/5、1/6、1/7、1/8、1/9。
74LS190的逻辑图见图6325。
它的功能表如表 635。
可以附加 必要的门电路。
【解】可用CP 0作为LD 信号。
因为在 CP 上升沿使Q 3Q 2QQ 0 = oooo 以后，在这个CP 的低电平期间CP 0将给出一个负脉冲。
但由于74LS190的LD = 0信号是异步置数信号，所以0000状态在计数过程中是作为暂态出现的。
