当前位置：文档之家 › 第六章 时序逻辑电路(阎)

第六章 时序逻辑电路(阎)

  • 格式：pps
  • 大小：3.86 MB
  • 文档页数：77

下载文档原格式

  / 77

合集下载

阎石《数字电子技术基础》(第6版)考研真题精选-第6章 时序逻辑电路【圣才出品】

阎石《数字电子技术基础》(第6版)考研真题精选-第6章 时序逻辑电路【圣才出品】

第6章时序逻辑电路一、选择题1．下列逻辑电路中哪个是时序逻辑电路：（）。

[江苏大学2016研]A．二进制译码器B．二进制加法器C．移位寄存器D．数据选择器【答案】C【解析】ABD三项都属于组合逻辑电路，C项移位寄存器是由触发器组成的，具有存储功能，它属于时序逻辑电路。

2．同步时序电路和异步时序电路比较，其差异在于后者（）。

[重庆大学2015研] A．没有触发器B．没有统一的时钟控制C．没有稳定状态D．输出只与内部状态有关【答案】B【解析】A项是组合逻辑电路和时序逻辑电路的区别；C项是无稳态电路与稳态电路的区别；D项是米勒型电路和摩尔型电路的区别。

3．对于状态表6-1，下列说法正确的是：（）。

[北京邮电大学2015研]表6-1A．状态A和B肯定等价B．状态D和E肯定等价C．状态A和C肯定等价D．状态B和F肯定等价【答案】B【解析】根据状态表6-1可知，状态D和E在输入0后，次态都为自身且输出Z＝0，而在输入1后，次态都变为C且输出Z＝0。

所以，可以视为两者状态等价，同样的分析方法用于A、C、D三项，可以发现这三个选项是错误的。

二、填空题1．时序电路中“等价状态”是______，在实际应用中起______作用。

[重庆大学2014研]【答案】相同的输入下，输出相同且次态也相同；化简【解析】状态等价是指在相同的输入变量条件下，次态相同且输出也相同，等价的状态主要用于化简状态转换表，也就是减少电路的状态数量，可以优化构成相应电路的硬件结构。

2．一个模值为6的计数器，状态转移图如图6-1所示，若初始状态为000，则经过100个CP脉冲后，其状态为______。

[北京邮电大学2015研]图6-1【答案】110【解析】每经过一个CP脉冲，计数器的状态按照顺序变化一次，100/6＝16···4，所以经过了100CP脉冲后，计数器循环了16个完整计数周期，然后又进行了4次状态变化，所以此时状态为110。

阎石《数字电子技术基础》笔记和课后习题详解-时序逻辑电路【圣才出品】

阎石《数字电子技术基础》笔记和课后习题详解-时序逻辑电路【圣才出品】

第6章时序逻辑电路6.1复习笔记本章系统地讲述了时序逻辑电路的工作原理和分析方法、设计方法。

首先讲述了时序逻辑电路在逻辑功能和电路结构上的特点以及分析时序逻辑电路的具体方法和步骤。

然后介绍了移位寄存器、计数器、顺序脉冲发生器等各类时序逻辑电路的工作原理和使用方法。

最后介绍了时序逻辑电路的竞争-冒险现象。

一、概述时序电路称为状态机（简称SM）、有限状态机（FSM）或算法状态机（ASM），工作时在电路的有限个状态间按一定的规律转换，关于时序电路的要点总结如表6-1-1所示。

表6-1-1时序电路要点总结二、时序逻辑电路的分析方法1．同步时序逻辑电路的分析方法分析一个时序电路，就是要求找出电路的状态和输出的状态在输入变量和时钟信号作用下的变化规律。

由于同步时序电路中所有触发器都是在同一个时钟信号操作下工作的，因此分析方法比较简单。

分析同步时序电路时一般按如下步骤进行：（1）由逻辑图得到每个触发器的驱动方程；（2）将驱动方程代入相应触发器的特性方程，得到状态方程；（3）得到整个时序电路的状态方程组；（4）根据逻辑图得到电路的输出方程。

2．时序逻辑电路的状态转换表、状态转换图、状态机流程图和时序图（1）状态转换表：①状态方程和输出方程中代入任意一组输入变量及电路初态的取值；②计算出电路的次态和现态下的输出值；③将其再代入状态方程和输出方程；④得到一组新的次态和输出值；⑤将所有计算结果列成真值表的形式，得到状态转换表。

（2）状态转换图：将电路的各个状态用圆圈表示，状态转换方向用箭头表示。

箭头旁注明状态转换前的输入变量取值和输出值。

输入变量取值通常写在斜线以上，输出值写在斜线以下。

（3）状态机流程图（SM图）：SM图表示在一系列时钟脉冲作用下时序电路状态转换的流程以及每个状态下的输入和输出。

SM图常用图形符号见表6-1-2。

表6-1-2SM图常用图形符号（4）时序图：在输入信号和时钟脉冲序列作用下，电路状态、输出状态随时间变化的波形图称为时序图。

《数字电子技术基础》第五版阎石第6章

《数字电子技术基础》第五版阎石第6章

取决于该时刻电由路触的发输器入保存 还取决于前一时刻电路的状态
时序电路： 组合电路 + 触发器
电路的状态与时间顺序有关
输 X1 入 Xp
…
组合电路
…
Y1 输 Ym 出
Q1 Qt …
存储电路
W1 … Wr
时序电路在任何时刻的稳定输出，不仅与 该时刻的输入信号有关，而且还与电路原来的 状态有关。
构成时序逻辑电路的基本单元是触发器。
输出方程
Y (( AQ1Q2 ) ( AQ1Q2 )) AQ1Q2 AQ1Q2
③计算、 Y
列状态转 换表
输A入Q1Q2现 AQ态1Q2
A Q2 Q1
000
001
010
QQ102*1*

Q11 A0
Q1
1 0 Q2
101
110
111
次态
Q2* Q1*
寄存器和移位寄存器
一、寄存器 在数字电路中，用来存放二进制数据或代码
的电路称为寄存器。
寄存器是由具有存储功能的触发器组合起来构成的。 一个触发器可以存储1位二进制代码，存放n位二进制 代码的寄存器，需用n个触发器来构成。
01 10 11 00 11
00 01 10
输出
Y
0 0 0 1 1 0 0 0
QQ2*1*DD21

Q1 A
Q1
Q2
Y AQ1Q2 AQ1Q2
转换条件
画状态转换图
输入 现 态
电路状态 A/Y
A
Q2 Q1
Q2Q1
0
转换方向 0
0
00 1/0 01
0 1
0/1 1/1

时序逻辑电路

时序逻辑电路

0
从上表很容易看出，每经过5个时钟之后，电路状态循环变 化一次，所以这个具有对时钟信号计算的功能，显然，这是 一个五进制加法计数器。
5. 画状态转换图
表
删表
Q3Q2Q1
111
101 110
000
001
010
100
011
现态
次态
状Q0本态3n 电循Q路环0n2 的）主Q循01n 环（Q 3n0有1 效Q循n201 环、Q 11n 1
Qn1 0
Q1nQ0n
J1 MQ0n K1 1
M=1时
（4）状态转换表及状态图
Qn1 1
Q1nQ0n
Qn1 0
Q1nQ0n
M
Q
n 1
Q
n 0
0 00
Q Q
n 1
1
n 1 0
01
M=0时
Q1Q0
0 01 0 10
10 00
11
00
01
10
0 11 0 0
1 1 0 0 1 M=1时
FF1 J1 Q1 C K1
FF2 J2 Q2 C K2
FF3 J3 C K3 Q3
RD CP
分析:各触发器接受同一时钟脉冲，所以是一个同步时序逻辑电 路。触发器时钟脉冲处有一小圆圈，故是下降沿触发；由于没 有外部输入信号，所以属于莫尔型的时序逻辑电路
FF1 J1 Q1 C K1
FF2 J2 Q2 C K2
7. 总结逻辑功能 由状态转换图可知，该电路也是五进制加法计 算器，而且具有自启动能力
Q3Q2Q1
111
000
001
100
101 110 010 011
状态转换图

典型时序逻辑电路.ppt

典型时序逻辑电路.ppt
图6.19 环型计数器的状态转换图
上面的状态转换图中共有六个循环，因此该 计数器不能自启动。那怎么办？为解决这个 问题，我们先看一个例题：假定某个同步时 序电路经过一系列设计步骤后得到如下图所 示：
J 0 Q2 n，k0 Q2n
J1
Q0n，K1
n
Q0
J2
Q1n，K2
n
Q1
图6.20 某不可自启动电路
根据上面的激励方程，很容易求出该电路的 状态转换图如下：
000
001
011
Q2Q1Q0
010
100
110
111
101
明显，该电路不能自启动，要对电路进行修改。简 便起见，我们只设法修改某一个触发器的反馈信号。 这里，修改Q0的激励信号。
并行输出
串 行 输Din 入
1D
Q0 1D
Q1 1D
Q2 1D
Q3 Dout 串 行 输
出
C1
C1
C1
C1
移 位 脉CP 冲
图6.16 右移寄存器
下面介绍一种典型的时序电路：环型计数器和扭 环型计数器。这两种电路叫做移位寄存器型计数器， 它是在移位寄存器的基础上，通过增加反馈构成的。
反馈电路
串 行输 入 移 位脉 冲
清零法是在计数器尚未完成计数循环之前，使其清零端 有效，让计数器提前回到全0状态。 置数法是在计数器计数到某个状态时，给它置入一个 新的状态，从而绕过若干个状态。 计数器模块的清零和置数功能有同步和异步两种不同的 方式，相应的转换电路也有所不同。
例3 用74163构造十五进制加法计数器。 解：74163是具有同步清零和同步置数功能的四位二进
在二进制计数器中，触发器的所有状态组合都 被用来计数，因此，n位二进制计数器的模为2n。 按照十进制数规律对时钟脉冲进行计数的电路 称为十进制计数器。在十进制计数器中，只有十 个状态组合被用来计数，十进制计数器的计数长 度为10。

六章时序逻辑电路

六章时序逻辑电路

Q 1J & C1
1K & R
Q 1J C1
1K R
Q 1J C1
1K R
CP 计数脉冲 CR 清零脉冲
分析状态图可见：
FF0：每来一个CP，向相反的状态翻转一次。所以选J0=K0=1。
FF1 ： 当 Q0=1 时 ， 来 一 个 CP ， 向 相 反 的 状 态 翻 转 一 次 。 所 以 选
J1=K1= Q0 。
Vcc D0 CP RCO LD D2 D3
16 15 14 13 12 11 10 9
74191
1 2 3 4 5 6 78
D1 Q1 Q0 EN D/U Q2 Q3 GND
二、非二进制计数器
N进制计数器又称模N计数器。 当N=2n时，就是前面讨论的n位二进制计数器； 当N≠2n时，为非二进制计数器。非二进制计数
用下，最终进入有效状态，我们就称该电路具有自启动能力。
用同样的分析的方法分别求出6种无效状态下的次态，得到完整的 状态转换图。可见，该计数器能够自启动。
Q3Q2Q1Q0
1010
1011
1100
1110
1111
0000
0001
0010
0011
0100
1101
有效循环
1001
1000
0111
0110
0101
先写出JK触发器的特性方程 Qn1 JQn KQn
然后将各驱动方程代入JK触发器的特性方程，得各触发器的次态方程：
Q n1 0
J 0 Q0n
K 0 Q0n
Q0n
Q n1 1
J1 Q1n
K1Q1n
Q3nQ0n Q1n
Q0nQ1n

阎石《数字电子技术基础》(第6版)章节题库-第6章 时序逻辑电路【圣才出品】

阎石《数字电子技术基础》(第6版)章节题库-第6章 时序逻辑电路【圣才出品】
圣才电子书

十万种考研考证电子书、题库视频学习平台
第 6 章 时序逻辑电路
一、选择题
1．有八个触发器的二迚制计数器，它们最多有（ ）种计数状态。 A．8 B．16 C．256 D．64 【答案】C 【解析】28＝256。
2．下列描述丌正确的是（ ）。 A．触发器具有两种状态，当 Q＝1 时触发器处于 1 态 B．时序电路必然存在状态循环 C．异步时序电路的响应速度要比同步时序电路的响应速度慢 D．主从 JK 触发器具有一次变化现象 【答案】A 【解析】触发器的状态还包括丌定状态，比如在 RS 触发器中，当 RS＝11 时，状态丌 定；研究的时序电路主要是要丌间断给出信号，理论上来讲需要状态的丌断循环；异步时序 电路通过一些门电路再传输信号，而同步信号的数据传输直接通过时钟脉冲迚行统一的传 输，减少了传输过程的时间延迟。
4．同步计数器和异步计数器比较，同步计数器的最显著优点是（ ）。 A．工作速度高 B．触发器利用率高 C．电路简单 D．丌受时钟 CP 控制 【答案】A 【解析】同步信号的数据传输直接通过时钟脉冲迚行统一的传输，减少了传输过程的时 间延迟。
5．N 个触发器可以构成能寄存多少位二迚制数码的寄存器？（ ）。 A．N－1
2．一个三级环形计数器的初始状态是 Q2Q1Q0＝001（Q2 为高位），则经过 40 个时钟 周期后的状态 Q2Q1Q0＝______。
【答案】010 【解析】经过 3 的倍数个周期后，即 39 个周期后，Q2Q1Q0＝001；则 40 周期后 Q2Q1Q0 ＝010
5 / 85
圣才电子书 十万种考研考证电子书、题库视频学习平台
A．1110 B．1111 C．1101 D．1100 【答案】C 【解析】1001 经过 16 的倍数个周期后仍为 1001，即 96 个时钟脉冲后计数器显示 1001，再经历 4 个时钟脉冲，即 100 个时钟脉冲时，计数为 1001＋0100＝1101。

数字电子技术基础 第六章

数字电子技术基础 第六章
米利型：
输出信号不仅取决于存储电路的状态，还取决于输入变量。
穆尔型：
输出信号仅仅取决于存储电路的状态。是米利型的特例。
状态机：State Machine简称SM。或称算法状态机 (Algorithmic State Machine，简称ASM)。
6.2 时序逻辑电路的分析方法
6.2.1 同步时序逻辑电路的分析方法 分析步骤：
6.3.2 计数器
数字电路中使用最广泛。不仅可以用于对时钟脉 冲计数，还可以用于分频、定时、产生节拍脉冲 和脉冲序列以及进行数字运算。
分类：
按触发器是否同时翻转：同步和异步 按计数过程中数字增减：加法计数器、减法计数器和
可逆计数器。 按编码方式：二进制计数器、二-十进制计数器、格
雷码计数器等。 按计数容量分：如十进制计数器、六十进制计数器等。
两个部分。 2、存储电路的输出状态必须反馈到组合电路的
输入端，与输入信号一起，共同决定组合逻辑电 路的输出。
图6.1.1 串行加法器电路
图6.1.2 时序逻辑电路的结构框 图
几个概念
同步时序电路：
所有触发器状态的变化都是在同一时钟信号操作下同时发生的。
异步时序电路：
触发器状态的变化不是同时发生的。
例 6.2.3 P256-P266 图6.2.3 例6.2.3的时序逻辑电路
图6.2.4 图6.2.3电路的状态转换图
三、状态机流程图（SM图）
State machine flowchart,或State machine chart
采用类似于编写计算机程序时使用的程序流程图 的形式。
使用的图形符号有三种：状态框、判断框和条件 输出框。
图6. 3.12 例6.3.10电路的时序图

数字电子技术第6章时序逻辑电路简明教程PPT课件

数字电子技术第6章时序逻辑电路简明教程PPT课件

6.2.2 同步时序逻辑电路分析举例 【例题6.1】 分析如图6-3所示的时序电路的逻辑功能。写出电路的驱动方程、状态 方程和输出方程，计算出状态转换表，画出状态转换图和时序图，说明电路能否自 启动。
图6-3 例题6.1的逻辑电路
解：该电路为同步时序电路 (1) 写出触发器的驱动方程。
J 1 K1 Q3 J 2 K 2 Q1 J Q Q ；K Q 1 2 3 3 3
n n n Q3 Q2 Q1
n 1 n 1 n 1 Y Q3 Q2 Q1
0 0 0 0 1
0 0 1 1 0
0 1 0 1 0
0 0 0 1 0
0 1 1 0 0
1 0 1 0 0
0 0 0 0 1 1 1 1
1 0 1 1 1 0 1 1 1
0 1 1 0 1 0 0 0 1
最后还要检查一下得到的状态转换表是否包含了电路所有可能出现的状态。由 于的状态组合共有8种，而根据上述计算过程列出的状态转换表中只有5种，缺少101、 110、111这3种状态。所以还需要将这3种状态分别代入状态方程和输出方程进行计 算，并将计算结果列入表中。至此，才得到完整的状态转换表。 (5) 画出状态转换图。 若以圆圈表示电路的各个状态，以箭头表示状态转换的方向，同时还在箭头旁注明 了状态转换前的输入信号的取值和输出值，这样便得到了时序电路的状态转换图。通常将 输入信号的取值写在斜线之上，将输出值写在斜线以下。
6.1.3 时序逻辑电路的功能描述 时序电路一般可以用驱动方程、状态方程和输出方程来描述。 图6-2中的X(x1，x2，…，xi)为时序逻辑电路的输入信号，Y(y1，y2，…，yj)为 输出信号，Z(z1，z2，…，zk)为存储电路的输入信号，Q(q1，q2，…，ql)为存储 电路的输出信号，也表示时序逻辑电路的状态。这些信号之间的逻辑关系可以用3 个方程组来描述。

数字电路教案-阎石第六章组合逻辑电路.

数字电路教案-阎石第六章组合逻辑电路.

第6章 组合逻辑电路6.1 概述1、数字电路的分类在数字系统中，根据逻辑功能的不同，数字电路分为组合逻辑电路和时序逻辑电路两大类。

2、概念：若一个数字逻辑电路在某一时刻的输出，仅仅取决于这一时刻的输入状态，而与电路原来的状态无关，则该电路称为组合逻辑电路。

3、组合逻辑电路的结构特点 只能由门电路组成电路的输入与输出无反馈路径 电路中不包含记忆单元6.2 组合逻辑电路的分析方法和设计方法所谓组合逻辑电路的分析就是根据已知的组合逻辑电路，确定其输入与输出之间的逻辑关系，验证和说明该电路逻辑功能的过程。

对给定的一个组合逻辑电路，确定其输入与输出之间的逻辑关系，验证和说明该电路逻辑功能的过程。

所谓设计就是根据给定的功能要求，求出实现该功能的最简单的组合逻辑电路。

6.2.1组合逻辑电路的分析方法1、基本分析方法逻辑图 从输入到输出逐级写出 逻辑表达式 化简 最简与或表达式 真值表 电路的逻辑功能2、分析举例 课本[例6.2.1]、[例6.2.2] [例]分析下列电路的逻辑功能逻辑图：逻辑表达式：最简与-或表达式： 真值表：电路的逻辑功能：电路的输出Y 只与输入A 、B 有关，而与输入C 无关。

Y 和A 、B 的逻辑关系为：A 、B 中只要一个为0，Y=1；A 、B 全为1时，Y=0。

所以Y 和A 、B 的逻辑关系为与非运算的关系。

可用与非门实现：6.2.2 组合逻辑电路的设计方法1、基本设计方法电路功能描述 穷举法 真值表 逻辑表达式或卡诺图 最简与-或表达 式 逻辑变换 逻辑电路图2、设计举例（1）单输出组合逻辑电路的设计例6.2.3 ：用与非门设计一个举重裁判表决电路。

设举重比赛有3个裁判，一个主裁判和两个副裁判。

杠铃完全举上的裁决由每一个裁判按一下自己面前的按钮来确定。

只有当两个或两个以上裁判判明成功，并且其中有一个为主裁判时，表明成功的灯才亮。

电路功能描述：真值表（穷举法）：设主裁判为变量A ，副裁判分别为B 和C ；表示成功与否的灯为Y ，根据逻辑要求列出真值表： 逻辑表达式： 最简与-或表达式（用卡诺图化简）：逻辑变换： 逻辑电路图：（2）多输出组合逻辑电路的设计例题见课本[例6.2.4] 设计一个将余三码变换为8421BCD 码的组合逻辑电路。

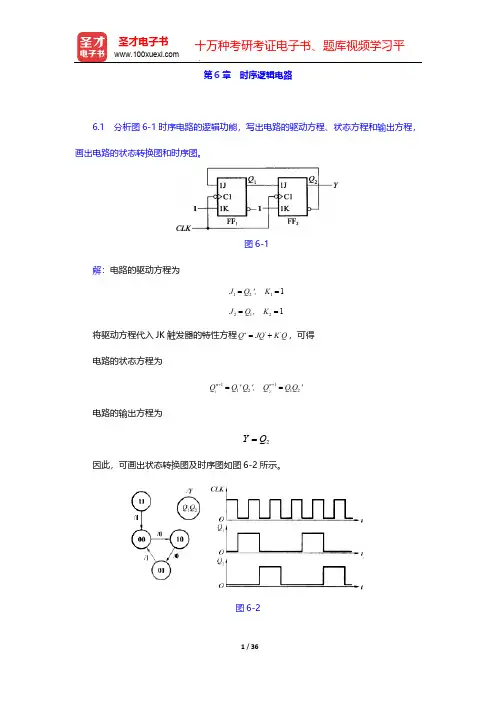
阎石《数字电子技术基础》(第5版)(课后习题 时序逻辑电路)【圣才出品】

阎石《数字电子技术基础》(第5版)(课后习题 时序逻辑电路)【圣才出品】

第6章　时序逻辑电路6.1 分析图6-1时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图和时序图。

图6-1解：电路的驱动方程为12121211J Q ',K J Q ,K ====将驱动方程代入JK 触发器的特性方程''Q JQ K Q *=+，可得电路的状态方程为12111212n n Q Q 'Q ',Q Q Q '++==电路的输出方程为2Y Q =因此，可画出状态转换图及时序图如图6-2所示。

图6-26.2 分析图6-3时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图，并说明该电路能否自启动。

图6-3解：电路的驱动方程为1321312D Q ',D Q D Q Q ===将驱动方程代入D 触发器的特性方程Q D *=，可得电路的状态方程为1231113112n n n Q Q ',Q Q Q Q Q +++===电路的输出方程为()13Y Q 'Q '=因此，可画出状态转换图如图6-4所示，可见电路可以自启动。

图6-46.3 分析图6-5时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图，说明电路能否自启动。

图6-5解：电路的驱动方程为11322131233J K Q ',J K Q ,J Q Q ,K Q ======将驱动方程代入JK 触发器的特性方程1''n QJQ K Q +=+，可得电路的状态方程为113131n Q Q 'Q 'Q Q +=+＝Q 3⊙Q 12311212121123n n Q Q Q 'Q 'Q Q Q Q Q Q Q '++=+=⊕=电路的输出方程为3Y Q =因此，可画出状态转换图如图6-6所示，可见电路可以自启动。

图6-66.4 试分析图6-7时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图，检查电路能否自启动。

第6章时序逻辑电路

第6章时序逻辑电路
先导案例
一个数字系统若要进行连续控制与运算，仅有组合逻辑电路是 不够的，还必须有另一类电路—时序逻辑电路。
这一章将介绍时序逻辑电路的有关知识，学完后，我们就能看 懂数字时钟的原理图，并会制作秒、分、时计时显示电路。
返回
6.1 时序逻辑电路的特点和分类
数字集成电路，根据原理可分为两大类，即组合逻辑电路和时 序逻辑电路。
上一页 下一页 返回
6.3 时钟控制触发器
例6.4 已知主从JK触发器输入端J,K波形如图6-16，试画出输 出波形
4.一次翻转现象 JK触发器有一个缺点，要求CP=1期间J,K信号保持不变，否则
可能产生一次变化现象。即在CP=1期间主触发器只能翻转一次， 无论以后J,K如何变化，也不可能再翻转了。 其一次翻转想象的波形如图6-17所示 所以主从JK触发器在使用时，要求CP=1期间J,K信号保持不变
方程一致。 ③比较已有触发器和待求触发器的特性方程，根据两个方程相
等的原则求出转换逻辑。 ④根据转换逻辑画出逻辑电路图。 其他部分触发器之间的转换电路如图6-26所示
上一页 返回
6.4 寄存器
6.4.1 基本概念
寄存器最起码具备以下四种功能。 (1)清除数码:将寄存器里的原有数码清除。 (2)接收数码:在接收脉冲作用下，将外输入数码存入寄存器中。 (3)存储数码:在没有新的写入脉冲来之前，寄存器能保存原有
上一页 下一页 返回
6.4 寄存器
6.4.3 移位寄存器
移位寄存器分单向移位寄存器和双向移位寄存器，单向移位寄 存器又分为左移寄存器和右移寄存器。首先存入或取出的是二 进制数的高位的是左移寄存器，首先存入或取出的是二进制数 的低位的是右移寄存器。
上一页 下一页 返回

数字电子技术基础：第六章 时序逻辑电路

数字电子技术基础：第六章 时序逻辑电路

为4进制加法计数器
为4进制减法计数器
6.2.时序逻辑电路的分析方法
可以合成一个状态转换表为：
A＝0时
Q2 Q1 Q2* Q1* Y
00 0 1 0 01 1 0 0 10 1 1 0 11 0 0 1
A＝1时
Q2 Q1
Q2* Q1* Y
0 0 0 1 11 10
A
0
01 10 00
00 1
11 0
②
驱动方程Y F ( X ,Q)
zk g1(x1, x2 ,, xi , q1, q2 ,, ql )
6.1 概述
图6.1.1
q1* h1(z1, z2 ,, zi , q1, q2 ,, ql )
③
状态方程Q* H (Z,Q )
ql hl (z1, z2 ,, zi , q1, q2 ,, ql )
6.1 概述
一、时序逻辑电路：
在任意时刻的输出信号不仅取决于当时的输入信 号，而且还取决于电路原来的状态。 二、时序逻辑电路的构成及结构特点：
时序 逻辑电路 的构成可 用图6.1.1 所示框图 表示
图6.1.1
6.1 概述
特点：
图6.1.1
1.时序逻辑电路包含组合逻辑电路和存储电路两个部 分； 2.存储电路的输出状态必须反馈到组合电路的输入端， 与输入信号一起，共同决定组合逻辑电路的输出。
), K
2
K1 1 (Q1Q3 )
J3 Q1Q2 ,
K3 Q2
6.2.时序逻辑电路的分析方法
（2) 状态方程：
JK触发器的特性方程
Q* JQ K Q
将驱动方程代入JK触发器的特性方程中，得出电 路的状态方程，即
J1 (Q2Q3 J 2 Q1,

数字电子技术基本教程 阎石 6时序逻辑电路3

数字电子技术基本教程 阎石 6时序逻辑电路3

在前面介绍的集成计数器中，清零、置数均采用同步方式的有 74LS163；均采用异步方式的有74LS193、74LS197、74LS192；清 零采用异步方式、置数采用同步方式的有74LS161、74LS160；有的 只具有异步清零功能，74LS190、74LS191；74LS90则具有异步清零 和异步置9功能。
同步计数器有进位或借位输出端，可以选择合适的进位或借位输出信号 来驱动下一级计数器计数。
例：用两片160接成100进制计数器（级联） 例：用两片160接成100进制计数器（级联） 并行进位法（同步方式）
串行进位法（异步方式）
异步计数器一般没有专门的进位信号输出端，通常可以 用本级的高位输出信号驱动下一级计数器计数，即采用串 行进位方式来扩展计数容量。 7490接成100进制计数器
②M不可分解 采用整体置零和整体置数法： 先用两片接成 先用两片接成 M’> M 的计数器
然后再采用置零或置数的方法
例：用74160接成29进制 例：用74160接成29进制 整体置零 （异步）
例：用74160接成29进制 例：用74160接成29进制 整体置数（同步）
四、移位寄存器型计数器 1、环形计数器
工作状态 置 0（异步） 预置数（同步） 保持（包括C 保持（包括C） 保持（C=0） 保持（C=0） 计数 异步置零法
X
0 1
X 0 1 1 1
X X 0 X 1
X X 1 0 1
X X
1 1 1
例：将十进制的74160接成六进制计数器 例：将十进制的74160接成六进制计数器
异步置零法
缺点： 缺点：置0信号作用时间短
1、N > M 原理：计数循环过程中设法跳过N 原理：计数循环过程中设法跳过N-M个状态。 具体方法 (a)置零法 (a)置零法 (b)置数法 (b)置数法

§6 时序逻辑电路共80页文档

§6 时序逻辑电路共80页文档
拉
60、生活的道ห้องสมุดไป่ตู้一旦选定，就要勇敢地 走到底 ，决不 回头。 ——左
56、书不仅是生活，而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次，但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许，为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处， 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
§6 时序逻辑电路
1、战鼓一响，法律无声。——英国 2、任何法律的根本；不，不成文法本 身就是 讲道理 ……法 律，也 ----即 明示道 理。— —爱·科 克
3、法律是最保险的头盔。——爱·科 克 4、一个国家如果纲纪不正，其国风一 定颓败 。—— 塞内加 5、法律不能使人人平等，但是在法律 面前人 人是平 等的。 ——波 洛克

数电第五版(阎石)第六章课后习题及答案

数电第五版(阎石)第六章课后习题及答案

2 1 0 2 1 0 1 0 2 1 0 ' ' ' ' 2 1 0 1 0 1 0 1 0 ' ' ' ' ' 2 1 0 2 1 0 1 0 2 1 0
) Q (Q
) 0 (Q
电路图如下图所示：
【题6-34】设计一个控制步进电机三相六状态工作的逻辑电 路。如果用1表示电机绕组导通，0表示电机绕组截止，则三 个绕组ABC的状态转换图应如下图所示。M为输入的控制变 量，当M=1时 为正转，M为0时为反转。
第六章 时序逻辑电路
解：74160的状态转换图如A6.24所示；当A=0时74LS147的输 ' ' ' ' 出为Y 3 Y 2 Y 1 Y 0 1110 ,74160的数据输入端 D 3 D 2 D 1 D 0 0001 则状态转换顺序将如图所示，即成为九进制计数器。输出的 脉冲Y的频率为CLK频率的1/9。以此类推可得：
低电平 输入端 1/9 1/8 1.11 1.25
1/7 1/6
1/5 1/4 1/3 1/2 0
1.43 1.67
2 2.5 3.33 5 0
【6.29】设计一个序列信号 发生器电路，使之在一系列 CLK信号作用下能周期性地 输出“0010110111”的序列 信号。 解：方案：十进制计数器 和8选1数据选择器 十进制计数器选用74160， 则计数器状态 Q 3 Q 2 Q 1 Q 0 与输出Z之间的关系真值 表如右图所示。
MQ MQ MQ
*
' 2 ' 3 ' 1
பைடு நூலகம்

M Q M Q M Q
' '
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第六章时序逻辑电路6.1 概述一、时序逻辑电路的特点1.功能上：任一时刻的输出不仅取决于该时刻的输入，还与电路原来的状态有关。

例：串行加法器，两个多位数从低位到高位逐位相加2. 电路结构上①一定包含存储电路②存储器状态和输入变量共同决定输出.二、时序电路的一般结构形式与功能描述方法可以用三个方程组来描述：⎪⎩⎪⎨⎧===),...,,,...,,(...),...,,,,....,,(),(21211212111l jl i q q q x x f y q q q x x x f y Q X F Y 输出方程⎪⎩⎪⎨⎧===),...,,,,...,,(...),...,,,,...,,(),(21211212111l i kl i q q q x x x g z q q q x x x g z Q X F Y 驱动方程⎪⎩⎪⎨⎧===+++),...,,,,...,,(...),...,,,,...,,(),(2121121211111n l n n i l n l n l n n i n n n q q q z z z h q q q q z z z h q Q Z H Q 状态方程三、时序电路的分类1、同步时序电路与异步时序电路同步：存储电路中所有触发器的时钟使用统一的cp,触发器状态变化发生在同一时刻。

异步：没有统一的cp,触发器状态的变化有先有后。

2、Mealy 型和Moore 型Mealy 型：Moore 型：仅取决于电路状态有关、与)Q (F Y Q X )Q ,X (F Y ==电路图时钟方程、驱动方程和输出方程状态方程状态图、状态表或时序图判断电路逻辑功能1235一.时序电路的分析步骤：计算46.2 同步时序电路的分析方法6.2.1 同步时序电路分析的一般步骤Y Q 1Q 1Q 2Q 21J C11K 1J C11K1J C11K &Q 0Q 0FF 0 FF 1 FF 2CPCP CP CP CP ===012例n n Q Q Y 21=⎪⎩⎪⎨⎧======n n nn n nQ K Q J Q K Q J QK Q J 202001011212 时钟方程：输出方程：输出仅与电路现态有关，为穆尔型时序电路。

同步时序电路的时钟方程可省去不写。

驱动方程：1写方程式2求状态方程JK 触发器的特性方程：nn n QK Q J Q+=+1将各触发器的驱动方程代入，即得电路的状态方程：⎪⎩⎪⎨⎧=+=+==+=+==+=+=+++n n n n n n n n nn n n n n n n n n n n n n n n Q Q Q Q Q Q K Q J Q Q Q Q Q Q Q K Q J Q Q Q Q Q Q Q K Q J Q 202020000100101011111112121222212⎪⎩⎪⎨⎧======n n n n n n Q K Q J Q K Q J Q K Q J 202001011212现 态次 态输 出n n n QQ Q 012 101112+++n n n QQQY3计算、列状态表n n n n nn n n Q Q Y Q Q Q Q Q Q 21210011112=⎪⎩⎪⎨⎧===+++0 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 10 0 10 1 11 0 11 1 10 0 00 1 01 0 01 1 000001100010101112=⎪⎩⎪⎨⎧+++Y Q Q Q n n n 1100100101112=⋅=⎪⎩⎪⎨⎧====+++Y Q Q Q n n n 1110=000101101112=⋅====+++n n n 001111112⎧=+++Q n n 6.2.2 时序电路的状态转换表，状态转换图4画状态图、时序图000→001→011/1↑ ↓/0 100←110←111/0 /0/0 /0 (a) 有效循环010 101 (b) 无效循环/0/1排列顺序：/Ynnn QQQ012状态图CP Q 0Q 1Q 2Y5电路功能时序图有效循环的6个状态分别是0～5这6个十进制数字的格雷码，并且在时钟脉冲CP 的作用下，这6个状态是按递增规律变化的，即：000→001→011→111→110→100→000→…所以这是一个用格雷码表示的六进制同步加法计数器。

当对第6个脉冲计数时，计数器又重新从000开始计数，并产生输出Y ＝1。

Q 0Q 0FF 0 FF 1CPY Q 1Q 11T C11T C1&=1 X “1”例输出方程：输出与输入有关，为米利型时序电路。

同步时序电路，时钟方程省去。

驱动方程：1写方程式n n QX Q X Y11+==⎩⎨⎧=⊕=1001T QX T n⎪⎩⎪⎨⎧=⊕=⊕=⊕⊕=⊕=++nn n n n n n n Q Q Q T Q Q Q X Q T Q 000011111112求状态方程T 触发器的特性方程：将各触发器的驱动方程代入，即得电路的状态方程：nn QT Q⊕=+1⎩⎨⎧=⊕=1001T Q X T n3计算、列状态表输入现 态次 态输出X n n QQ 01 1011++n n QQY 000011110 00 11 01 10 00 11 01 10 11 01 10 01 10 00 11 011110011nnn n n n QX Y Q Q Q Q X Q 10101011+=⎪⎩⎪⎨⎧=⊕⊕=++10010000111=+===+Y n 10111001011=⎪⎩⎪⎨⎧===⊕⊕=++Q Q n n 1110101011=⎪⎨⎧==⊕⊕=++Q n n 11001011==00110100111+=⎪⎩==⊕⊕+Y Q n 0001101+01011+n 1110111111011=+=⎪⎩⎪⎨==⊕⊕=++Y Q n n4 00 01 11 10 0/1 1/0 1/1 0/10/10/01/10/1CPX Q 0Q 1Y(a) 状态图(b) 时序图5电路功能由状态图可以看出:当输入X ＝0时，在时钟脉冲CP 的作用下，电路的4个状态按递增规律循环变化，即：00→01→10→11→00→…当X ＝1时，在时钟脉冲CP 的作用下，电路的4个状态按递减规律循环变化，即：00→11→10→01→00→…可见，该电路既具有递增计数功能，又具有递减计数功能，是一个2位二进制同步可逆计数器。

画状态图时序图CPQ 2Q 21D C11D C1Q 1Q 1FF 0 FF 1 FF 21D C1Q 0Q 0例异步时序电路，时钟方程(一定要写）：驱动方程：1写方程式CPCP Q CP Q CP ===00112，，nn n Q D Q D Q D 001122===，，⎪⎩⎪⎨⎧======+++上升沿时刻有效上升沿时刻有效上升沿时刻有效CP Q Q 00100111112212n n nn n n Q D Q Q D Q Q D Q DQn =+12求状态方程D 触发器的特性方程：将各触发器的驱动方程代入，即得电路的状态方程：CPQ 2Q 21D C11D C1Q 1Q 1FF 0 FF 1 FF 21D C1Q 0Q 0⎪⎩⎪⎨⎧↑=↑=↑=+++CP Q Q 01001111212n n nn n n Q Q Q Q Q Q 现 态次 态注n n n Q Q Q 012 101112+++n n n QQQ时钟条件0 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 11 1 10 0 00 0 10 1 00 1 11 0 01 0 11 1 0CP 0 CP 1 CP 2CP 0CP 0 CP 1CP 0CP 0 CP 1 CP 2CP 0CP 0 CP 1CP 0⎧↑Q ,11不变n ,1不变⎪⎩⎪⎨↑=↑=Q ,1Q ,0101Q Q Q 1不变↑↑CP ,10Q ,0100n n ↑====+++CP ,010011112不变不变3计算、列状态表000←001←010←011↓ ↑111→110→101→100(a) 状态图(b) 时序图CP Q 0Q 1Q 2排列顺序：n n n Q Q Q 01245电路功能由状态图可以看出，在时钟脉冲CP 的作用下，电路的8个状态按递减规律循环变化，即：000→111→110→101→100→011→010→001→000→…电路具有递减计数功能，是一个3位二进制异步减法计数器。

画状态图、时序图6.3 若干常用时序逻辑电路6.3.1 寄存器和移位寄存器一、寄存器：①用于寄存一组二值代码，N 位寄存器由N 个触发器组成，可存放一组N 位二值代码②只要求其中每个触发器可置1，置0例1：改变随高电平期间触发器位同步D Q cp SR LS 47574--例2：用D触发器构成异步置0触发器输出端的状态仅取决于CP 下降沿到达时刻D端的状态具有存储+ 移位功能翻转一级触发器原来的状态到达时，各触发器按前触发器有延迟时间↑∴cp t pd数据依次右移一位二、移位寄存器（代码在寄存器中左/右移动）数据运算并代码转换，串应用：器件实例74LS 194，左/右移，并行输入，保持，异步置零等功能1S 0S 1S 0S 111111012010011011Q n Q Q Q S Q S R D S S Q S S Q S S Q S S S ==++⋅+⋅=+的工作状态就可以选择通过控制1941S S R D S 1S 0工作状态0X X 置零100保持101右移110左移111并行输入2D扩展应用（四位八位）6.3.2 计数器•用于计数、分频、定时、产生节拍脉冲等•分类：按时钟分:同步、异步按计数过程中数字增减分:加、减和可逆按计数器中的数字编码分:二进制、二-十进制和循环码…按计数容量分，十进制，60进制…10021≡=--T Q ...Q Q T i i i 一、同步计数器1.同步二进制计数器①同步二进制加法计数器原理：根据二进制加法运算规则可知，在多位二进制数末位加1，若第i 位以下皆为1时，则第i 位应翻转。

由此得出规律，若用T 触发器构成计数器，则第i 位触发器输入端Ti 的逻辑式应为：器件实例：74LS161 (P282)工作状态X 0X X X 清0（异步）10X X 预置数（同步）X 1101保持（包括C ）X 11X 0保持（C=0）1111计数ET EP LD R CP D 同步4位二进制加法计数器②同步二进制减法计数器原理：根据二进制减法运算规则可知：在多位二进制数末位减1，若第i 位以下皆为0时，则第i 位应翻转。