当前位置：文档之家 › 第6章-时序逻辑电路.

第6章-时序逻辑电路.

  • 格式：doc
  • 大小：2.16 MB
  • 文档页数：31

下载文档原格式

  / 31

合集下载

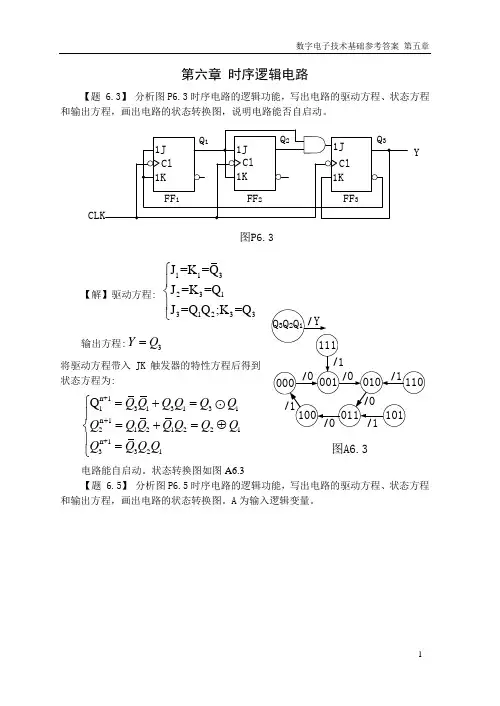
第6章_时序逻辑电路 课后答案

第6章_时序逻辑电路 课后答案

第六章 时序逻辑电路【题 6.3】 分析图P6.3时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图，说明电路能否自启动。

Y图P6.3【解】驱动方程:11323131233J =K =Q J =K =Q J =Q Q ;K =Q ⎧⎪⎨⎪⎩ 输出方程:3YQ =将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+11313131n 12121221n+13321Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q +⎧=+=⎪=+=⊕⎨⎪=⎩ 电路能自启动。

状态转换图如图A6.3【题 6.5】分析图P6.5时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图。

A 为输入逻辑变量。

图A6.3Y图P6.5【解】驱动方程: 1221212()D AQ D AQ Q A Q Q ⎧=⎪⎨==+⎪⎩输出方程: 21Y AQ Q =将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+112n+1212()Q AQQ A Q Q ⎧=⎪⎨=+⎪⎩ 电路的状态转换图如图A6.51图A6.5【题 6.6】 分析图P6.6时序电路的逻辑功能，画出电路的状态转换图，检查电路能否自启动，说明电路能否自启动。

说明电路实现的功能。

A 为输入变量。

AY图P6.6【解】驱动方程: 112211J K J K A Q ==⎧⎨==⊕⎩输出方程: 1212Y AQ Q AQ Q =+将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+111n+1212QQ Q A Q Q ⎧=⎪⎨=⊕⊕⎪⎩ 电路状态转换图如图A6.6。

A ＝0时作二进制加法计数，A ＝1时作二进制减法计数。

01图A6.6【题 6.7】 分析图P6.7时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图，说明电路能否自启动。

Y图P6.7【解】驱动方程: 001023102032013012301;;;J K J Q Q Q K Q J Q Q K Q Q J Q Q Q K Q==⎧⎪=•=⎪⎨==⎪⎪==⎩ 输出方程: 0123Y Q Q Q Q =将驱动方程带入JK 触发器的特性方程后得到状态方程为:*00*1012301*2023012*3012303()Q ()Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q⎧=⎪=++⎪⎨=++⎪⎪=+⎩ 设初态Q 1Q 3Q 2Q 1 Q 0=0000，由状态方程可得：状态转换图如图A6.7。

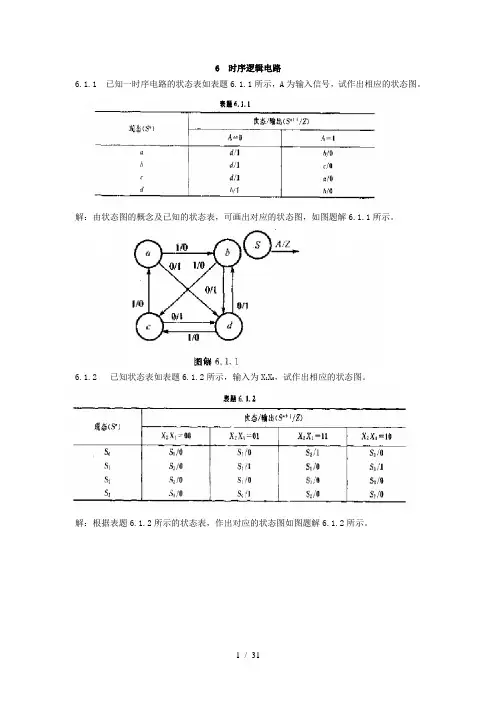
第6章 时序逻辑电路

第6章 时序逻辑电路

J 和 K 接为互反，相当于一个D触发器。时钟相连 是同步时序电路。
电路功能： 有下降沿到来时，所有Q端更新状态。
2、移位寄存器 在计算机系统中，经常要对数据进行串并转换，移 位寄存器可以方便地实现这种转换。
左移移位寄存器
•具有左右移位功能的双向移位寄存器
理解了前面的左移移位寄存器，对右移移位寄存器 也就理解了，因位左右本身就是相对的。实际上，左右 移位的区别在于：N触发器的D端是与 Q N+1相连，还是 与Q N-1相连。
第六章 时序逻辑电路
如前所述，时序逻辑电路的特点是 —— 任一时刻 的输出不仅与当前的输入有关，还与以前的状态有关。
时序电路以触发器作为基本单元，使用门电路加以 配合，完成特定的时序功能。所以说，时序电路是由组 合电路和触发器构成的。
与学习组合逻辑电路相类似，我们仍从分析现成电 路入手，然后进行时序逻辑电路的简单设计。
状态化简 、分配
用编码表示 给各个状态
选择触发器 的形式
确定各触发器 输入的连接及 输出电路
NO 是否最佳 ？
YES
设计完成
下面举例说明如何实现一个时序逻辑的设计：
书例7-9 一个串行输入序列的检测电路，要求当序
列连续出现 4 个“1”时，输出为 1，作为提示。其他情 况输出为 0。
如果不考虑优化、最佳，以我们现有的知识可以很
第二步： 状态简化
前面我们根据前三位可能的所有组合，设定了 8 个
状态A ~ H，其实仔细分析一下，根本用不了这么多状态。
我们可以从Z=1的可能性大小的角度，将状态简化为
4 个状态：
a
b
c
d
A 000
B 100
D 110

数字电子技术基础-第六章_时序逻辑电路(完整版)

数字电子技术基础-第六章_时序逻辑电路(完整版)

T0 1
行修改，在0000 时减“1”后跳变 T1 Q0 Q0(Q3Q2Q1)
为1001，然后按
二进制减法计数
就行了。T2 Q1Q0 Q1Q0 (Q1Q2Q3 )
T3 Q2Q1Q0
50
能自启动
47
•时序图 5
分 频
10 分 频c
0
t
48
器件实例：74 160
CLK RD LD EP ET 工作状态 X 0 X X X 置 0（异步） 1 0 X X 预置数（同步） X 1 1 0 1 保持（包括C） X 1 1 X 0 保持（C=0） 1 1 1 1 计数
49
②减法计数器
基本原理：对二进 制减法计数器进
——74LS193
异步置数 异步清零
44
（采用T’触发器，即T=1）

CLKi
CLKU
i 1
Qj
j0
CLKD
i 1
Qj
j0

CLK0 CLKU CLKD
CLK 2 CLKU Q1Q0 CLK DQ1Q0
45
2. 同步十进制计数器 ①加法计数器
基本原理：在四位二进制 计数器基础上修改，当计 到1001时，则下一个CLK 电路状态回到0000。
EP ET 工作状态
X 0 X X X 置 0（异步）
1 0 X X 预置数（同步）
X 1 1 0 1 保持（包括C）
X 1 1 X 0 保持（C=0）
1 1 1 1 计数
39
同步二进制减法计数器 原理：根据二进制减法运算 规则可知：在多位二进制数 末位减1，若第i位以下皆为 0时，则第i位应翻转。
Y Q2Q3

第6章-时序逻辑电路

第6章-时序逻辑电路

6 时序逻辑电路6.1.1 已知一时序电路的状态表如表题6.1.1所示，A为输入信号，试作出相应的状态图。

解：由状态图的概念及已知的状态表，可画出对应的状态图，如图题解6.1.1所示。

6.1.2已知状态表如表题6.1.2所示，输入为X1X0，试作出相应的状态图。

解：根据表题6.1.2所示的状态表，作出对应的状态图如图题解6.1.2所示。

6.1.3已知状态图如图题6.1.3所示，试列出它的状态表。

解：按图题6.1.3列出的状态表如表题解6.1.3所示。

6.1.5 图题6.1.5所示是某时序电路的状态图，设电路的初始状态为01，当序列A=100110（自左至右输入）时，求该电路输出Z的序列。

解：由图题6.1.5所示的状态图可知，当初态为01，输入信号的序列A=100110时，该时序电路将按图题解6.1.5所示的顺序改变状态，因而对应的输出序列为Z=011010。

6.1.6已知某时序电路的状态表如表题6.1.6所示，输入A，试画出它的状态图。

如果电路的初始状态在b，输入信号A一次是0、1、0、1、1、1、1，试求出其相应的输出。

解：根据表题6.1.6所示的状态表，可直接画出与其对应的状态图，如图题解6.1.6（a）当从初态b开始，依次输入0、1、0、1、1、1、1信号时，该时序电路将按图题解6.1.6（b）所示的顺序改变状态，因而其对应的输出为1、0、1、0、1、0、1。

6.2 同步时序逻辑电路的分析6.2.1 试分析图题6.2.1（a）所示时序电路，画出其状态表和状态图。

设电路的初始状态为0，试画出6.2.1（b）所示波形作用下，Q和Z的波形图。

解：由所给电路图可写出该电路的状态方程和输出方程，分别为1n nQ A QZAQ+=⊕=其状态表如表题解6.2.1所示，状态图如图题解6.2.1（a）所示，Q和Z的波形图如图题解6.2.1（b）所示。

6.2.2 试分析图题6.2.2（a）所示时序电路，画出其状态表和状态图。

数字电子技术第6章 时序逻辑电路

数字电子技术第6章 时序逻辑电路

RD—异步置0端（低电平有效） 1 DIR—右移串行输入 1 DIL—左移串行输入 S0、S1—控制端 1 D0D1 D2 D3—并行输入
《数字电子技术》多媒体课件
山东轻工业学院
4、扩展：两片74LS194A扩展一片8位双向移位寄存器
《数字电子技术》多媒体课件
山东轻工业学院
例6.3.1的电路 （P276) 74LS194功能 S1S0=00,保持 S1S0=01,右移 S1S0=10,左移 S1S0=11,并入
（5）状态转换图
《数字电子技术》多媒体课件
山东轻工业学院
小结
1、时序逻辑电路的特点、组成、分类及描述方法； 2、同步时序逻辑电路的分析方法； 课堂讨论： 6.1，6.4
《数字电子技术》多媒体课件
山东轻工业学院
6.3 若干常用的时序逻辑电路
寄存器和移位寄存器 时序 逻辑电路 计数器 顺序脉冲发生器 序列信号发生器
移位寄存器不仅具有存储功能，且还有移位功能。 可实现串、并行数据转换，数值运算以及数据处理。 所谓“移位”，就是将寄存器所存各位数据，在每个移 位脉冲的作用下，向左或向右移动一位。
2、类型： 根据移位方向，分成三种：
左移 寄存器 (a) 右移 寄存器 (b) 双向 移位 寄存器 (c)
《数字电子技术》多媒体课件
学习要求 ：
* *
自学掌握
1. 掌握寄存器和移位寄存器的概念并会使用； 2. 掌握计数器概念，熟练掌握中规模集成计数器74161 和74160的功能，熟练掌握用160及161设计任意进制计 数器的方法。
《数字电子技术》多媒体课件
山东轻工业学院
6.3.1寄存器和移位寄存器
一、寄存器
寄存器是计算机的主要部件之一， 它用来暂时存放数据或指令。

第6章时序逻辑电路

第6章时序逻辑电路
1、反馈置0法 反馈置0法的基本思想是： 计数器从全0状态S0开始计数，计满M个状态产生置0信 号，使计数器恢复到初态S0,然后再重复前面过程。
☆ 选择模M计数器的计数范围，确定初态和末态。
☆ 确定产生置0或置数信号的译码状态，然后根据译码 状态设计译码反馈电路，是计数器产生清0或置数信号。
☆ 画出实现模N计数器的逻辑电路。
TP TT
1 0
,
触发器保持，CO
0
1
C C
TP TT
0 1
,
触发器保持，CO
Q0 Q3
计1 数1条件1 ↑ X X X X
计数
1 0 X X X X X X 保持，C0=0
1 1 0 X X X X X 保持CO=Q0~Q3
M＝16二进制计数器 逢十六进一
内部逻辑电路图
中 规模集 成电 路由四 级 JK 触发器和若干门电路组成，其内 部电路如图所示。
CP 8 4 2 C1 R
CTP LD D3D2D1D0
CTT 74160(2)CO
CP 8 4 2 1CR
CTP LD D3D2D1D0
CTT 74160(3)CO
CP 8 4 2 1 CR
所以第853个状态
&
不计算在主循环内
由前面例题分析中可以发现，用反馈置0法设计计数 器存在一个普遍规律，有待于我们去总结。
74161是M16二进制计数器，只能实现M16以下任意进制数。
例、用74161组成十进制(N=10)计数器
解： 先将74161接成M16计数器， CR,LD,CTT,CTP均＝1
然后作跳过六个状态（M-N =16-10=6）的十进制计数器，将模M计数
器变为模N计数器。

第六章 时序电路

第六章 时序电路
状态有关。 构成时序逻辑电路的基本单元是触发器。
二、时序逻辑电路的分类：
按 动 作 特 点 可 分 为
同步时序逻辑电路
所有触发器状态的变化都是在 同一时钟信号操作下同时发生。
异步时序逻辑电路
触发器状态的变化不是同时发生。
按 输 出 特 点 可 分 为
米利型时序逻辑电路(Mealy)
输出不仅取决于存储电路的状态，而且还 决定于电路当前的输入。
Q2 Q1 Q0
/Y
/0 /0 000→001→011 /1↑ ↓/0
CP Q0 010 Q1 Q2 Y
/0 101 /1 (b) 无效循环
100←110←111 /0 /0 (a) 有效循环
有效循环的6个状态分别是0～5这6个十进制数
字的格雷码，并且在时钟脉冲CP的作用下，这6个
状态是按递增规律变化的，即： 000→001→011→111→110→100→000→… 所以这是一个用格雷码表示的六进制同步加法 计数器。当对第6个脉冲计数时，计数器又重新从 000开始计数，并产生输出Y
Q=0时
LED亮
RD Q0 Q1 D1 Q2 D2 D3 Q3 S1
DIR D0 D1D2D3S0 DIL CLK +5V
74LS194
DIR D0
S0 DIL CLK +5V
清0按键 1秒
S1=0,S0=1
CLK 右移控制
本节小结：
寄存器是用来存放二进制数据或代
码的电路，是一种基本时序电路。任何
画状态转换图
Q3Q2Q1 /Y
000
/1 /1 111
/0
001
/0
010
/0
011 /0

第6章_时序逻辑电路

第6章_时序逻辑电路

数字电子技术（第5版）第6章时序逻辑电路1.(334)利用（）可以把集成计数器设计成初态不为零的计数器。

答案.反馈置数法2.(318)时序逻辑电路由( ) 和( ) 两部分组成。

答案.组合电路存储电路3.(337)一个4位的扭环形计数器有（）个状态。

答案. 84.(335)集成计数器的级联方式有（）和（）两种方式。

答案.异步同步5.(333)利用（）和（）可以改变集成计数器的计数长度。

答案.反馈归零法反馈置数法6.(332)一个模为24的计数器，能够记录到的最大计数值是（）。

答案. 237.(331)计数器的模表示计数器的（）计数长度。

答案.最大8.(329)构成时序电路的各触发器的时钟输入端都接在一起，这种时序电路称为（）。

答案.同步时序电路9.(328)时序电路的输出不仅与电路的（）有关，还与电路的（）有关。

答案.现态输入信号10.(327)摩尔型时序电路的输出仅由电路的（）决定，而与电路的( ) 无关。

（注：教材中没有讲述摩尔型电路的概念，故删去此题）答案.现态输入信号11.(326) 时序逻辑电路的功能描述有 ( ) 、 ( ) 、 ( ) 、 ( ) 。

答案. 逻辑方程式 状态表 状态图 时序图12.(330) 异步时序电路中的各触发器的状态转换 （ ）同一时刻进行的。

答案. 不是在13.(336) 一个4位的环形计数器有（ ）个状态。

答案. 414.(325) 时序逻辑电路可分为 （ ） 和 ( ) 两大类。

答案. 同步时序电路 异步时序电路15.(354) 分析如图7307所示电路，说明其功能。

图7307输 入输 出CR LD T CT P CT CP 3D 2D 1D 0D 3Q 2Q 1Q 0QCO0 × × × × × × × × 000 10××↑3d 2d 1d 0d 3d 2d 1d 0d1111↑×××× 计数 110×××××× 保持 11××××××保持答案. 经分析知，采用了74LS160的同步置数功能。

数字电路与逻辑设计微课版(第6章 时序逻辑电路)教案

数字电路与逻辑设计微课版(第6章 时序逻辑电路)教案

第6章时序逻辑电路本章的主要知识点时序逻辑电路的基本知识、时序逻辑电路的分析和设计、关于自启动的修正问题、常用的中规模时序电路。

1.参考学时10学时（总学时32学时，课时为48课时可分配12学时）。

2.教学目标（能力要求）●掌握同步时序逻辑电路的分析和设计方法；●掌握电路挂起的修正方法；●掌握常用的中规模时序逻辑电路（计数器、寄存器）的外部特性及使用方法；●掌握脉冲异步时序逻辑电路的分析和设计方法；●掌握中规模时序逻辑电路的分析和设计方法。

3.教学重点●同步时序逻辑电路的设计：包括设计中的原始状态图、状态表、状态化简、状态编码、确定激励函数和输出函数等；●同步时序逻辑电路的自启动的分析：能根据设计好的电路分析电路是否存在自启动的问题，并学会修正它。

●脉冲异步时序逻辑电路的分析和设计方法：了解和同步时序逻辑电路的分析和设计方法的差异性，并熟练掌握脉冲异步时序逻辑电路的分析和设计方法●中规模时序逻辑电路的外部特性及使用方法：通过理论分析来学习常用中规模时序逻辑电路的外部特性及使用方法，通过具体实例来学习中规模时序逻辑电路的分析和设计方法4.教学难点●原始状态图：学生开始不知道如何增加状态，什么时候增加状态●自启动的修正：学生能分析出挂起，但是对于修正比较困难●脉冲异步时序逻辑电路的分析：当脉冲异步时序逻辑电路的存储电路是没用统一时钟端的钟控触发器时，如何分步找到每个触发器的时钟的跳变时刻对学生来说是一大挑战●计数器的使用方法：掌握置数法、清零法、级联法实现任意模的计数器5.教学主要内容（1）时序逻辑电路概述（15分钟）（2）小规模时序逻辑电路分析（120分钟）➢小规模时序逻辑电路的分析方法和步骤➢小规模同步时序逻辑电路的分析➢小规模异步时序逻辑电路的分析（3）小规模时序逻辑电路设计（180分钟）➢小规模时序逻辑电路的设计方法和步骤➢小规模同步时序逻辑电路的设计➢小规模异步时序逻辑电路的设计（4）常用中规模时序逻辑电路（45分钟）➢集成计数器➢寄存器（5）中规模时序逻辑电路的分析和设计（90分钟）➢中规模时序逻辑电路的分析➢中规模时序逻辑电路的设计6.教学过程与方法（1）时序逻辑电路概述（15分钟）简要介绍时序逻辑电路的结构、特点、分类和描述方法等。

数电第六章时序逻辑电路

数电第六章时序逻辑电路

• 根据简化的状态转换图，对状态进行编码，画出编码形式 的状态图或状态表
• 选择触发器的类型和个数 • 求电路的输出方程及各触发器的驱动方程 • 画逻辑电路图，并检查电路的自启动能力 EWB
典型时序逻辑集成电路
• 寄存器和移位寄存器 – 寄存器 – 移位寄存器 –集成移位寄存器及其应用 • 计数器 – 计数器的定义和分类 – 常用集成计数器 • 74LVC161 • 74HC/HCT390 • 74HC/HCT4017 – 应用 • 计数器的级联 • 组成任意进制计数器 • 组成分频器 • 组成序列信号发生器和脉冲分配器
– 各触发器的特性方程组：Q n1 J Q n KQ n CP
2. 将驱动方程组代入相应触发器的特性方程,求出各触发器 的次态方程,即时序电路的状态方程组
n n FF0：Q0 1 Q 0 CP n n n FF1：Q1 1 A Q0 Q1 CP
同步时序逻辑电路分析举例(例6.2.2C)
分析时序逻辑电路的一般步骤
• 根据给定的时序电路图写方程式 – 各触发器的时钟信号CP的逻辑表达式(同步、异步之分) – 时序电路的输出方程组 – 各触发器的驱动（激励）方程组 • 将驱动方程组代入相应触发器的特性方程,求出各触发器 的次态方程,即时序电路的状态方程组 • 根据状态方程组和输出方程组,列出该时序电路的状态 表,画状态图或时序图 • 判断、总结该时序电路的逻辑功能
• 电路中存在反馈
驱动方程、激励方程: E F2 ( I , Q )
状态方程 : Q n1 F3 ( E , Q n ) • 电路状态由当前输入信号和前一时刻的状态共同决定
• 分为同步时序电路和异步时序电路两大类
什么是组合逻辑电路?

数字电路第6章(1时序逻辑电路分析方法)

数字电路第6章(1时序逻辑电路分析方法)

数字电路第6章(1时序逻辑电路分析方法)1、第六章时序规律电路本章主要内容6.1概述6.2时序规律电路的分析方法6.3若干常用的时序规律电路6.4时序规律电路的设计方法6.5时序规律电路中的竞争-冒险现象1.时序规律电路的特点2.时序规律电路的分类3.时序规律电路的功能描述方法§6.1概述一、时序规律电路的特点1、功能：任一时刻的输出不仅取决于该时刻的输入；还与电路原来的状态有关。

例:串行加法器:两个多位数从低位到高位逐位相加一、时序规律电路的特点2.电路结构①包含存储电路和组合电路，且存储电路必不行少；②存储电路的输出状态必需反馈到组合电路输入端，与输入变量共同确定组合规律的输出。

yi:输出信号xi:输2、入信号qi:存储电路的状态zi:存储电路的输入可以用三个方程组来描述：Z=G(X,Q)二、时序电路的分类1.依据存储电路中触发器的动作特点不同时序电路存储电路里全部触发器有一个统一的时钟源;触发器状态改变与时钟脉冲同步.同步：异步：没有统一的时钟脉冲，电路中要更新状态的触发器的翻转有先有后，是异步进行的。

二、时序电路的分类2.依据输出信号的特点不同时序电路输出信号不仅取决于存储电路的状态，而且还取决于输入变量。

Y=F(X,Q)米利(Mealy)型：穆尔(Moore)型：输出状态仅取决于存储电路的状态。

犹如步计数器Y=F(Q)三、时序规律电路的功能描述方法描述方法3、规律方程式状态转换表状态转换图时序图三、时序规律电路的功能描述方法(1)规律方程式：写出时序电路的输出方程、驱动方程和状态方程。

输出方程反映电路输出Y与输入X和状态Q之间关系表达式；驱动方程反映存储电路的输入Z与电路输入X和状态Q之间的关系状态方程反映时序电路次态Qn+1与驱动函数Z和现态Qn之间的关系三、时序规律电路的功能描述方法(2)状态〔转换〕表：反映输出Z、次态Qn+1和输入X、现态Qn间对应取值关系的表格。

(3)状态〔转换〕图：(4)时序图：反映时序规律电路状态转换规律及相应输入、输出取值关系的有向图形。

第六章时序逻辑电路

第六章时序逻辑电路
异步 置0端
CLK异0为步计计数数输器入与端、同Q步0为计输数出器端比，二，进具制有计如数下器 特点： CLK* 1电为计路数简输单入；端、Q3为输出端，五进制计数器 CLK* 1速与Q度0慢相连；、CLK0为输入端、Q3为输出端，十进制计数器
四、任意进制计数器的构成方法 设已知计数器的进制为N,要构成的任意进制计数
圆圈表示电路的各个状态，箭头表示状态表示的方向， 箭头旁注明转换前的输入变量取值和输出值
三、状态机流程图（SM图） 采用类似于编写计算机程序时使用的程序流程图的形
式，表示在一系列时钟脉冲作用下时序电路状态的流程以及 每个状态下的输入和输出。
四、时序图 在输入信号和时钟脉冲序列作用下，电路状态、
输出状态随时间变化的波形图。
电路在某一给定时刻的输出
取决于该时刻电路由的触输发入器保存 还取决于前一时刻电路的状态
时序电路： 组合电路 + 触发器
电路的状态与时间顺序有关
例：串行加法器电路
利用D触发器 把本位相加后 的进位结果保 存下来
时序电路在结构上的特点：
（1）包含组合电路和存储电路两个组成部分
（2）存储输出状态必须反馈到组合电路的输入端，与输入 信号共同决定组合逻辑电路的输出
串行进位方式以低位片的进位输出信号作为高位片的时 钟输入信号;
并行进位方式以低位片的进位输出信号作为高位片的 工作状态控制信号（计数的使能信号），两片的CLK同时接 计数输入信号。
二、异步计数器
B、减法计数器
二、异步计数器
B、减法计数器
根据T触发器的翻转规律即可画出在一系列CLK0脉冲信号 作用下输出的电压波形。
2、异步十进制计数器
J K端悬空相当于接逻辑1电平 将4位二进制计数器在计数过程中跳过从1010到1111这6个状态。

数字电子技术课件第六章 时序逻辑电路(调整序列码)0609

数字电子技术课件第六章 时序逻辑电路(调整序列码)0609

（3）移入数据可控的并行输入移位寄存器
Z
M
Z D3 X Q3MX Q3NX
N 0 1 0 1
Q3n+1 置0 Q3不变 Q3计翻 置1
0 0 1 1
X 0, Z D3 同步（并行）置数 X 1, Z M Q3 NQ3 右移
右移数据由MN组合而定
3、双向移位寄存器 加选通门构成。
t1
t2
t3
存1 个 数 据 占 用1 个 cp
D1 D2 D3、 Q1 Q2 Q3波形略
二、移位寄存器
移位：按指令(cp),触发器状态可 向左右相邻的触发器传递。 功能：寄存，移位。
构成：相同的寄存单元（无空翻触发器）
共用统一的时钟脉冲（同步工作） 分类：单向、双向
1、单向移位寄存器（4位，右移为例，JK触发器构成） （1）电路：4个相同寄存单元(4个JK触发器)； 同步cp为移位指令； 移1(即: Qn+1 =1) → J=1，K=0 移0(即: Qn+1 =0) → J=0，K=1
1
4个脉冲以后 可从Q3～Q0并 行输出1101
2、并行输入移位寄存器
可预置数的移 位寄存器
（1）选通门——与或逻辑，2选1数据选择器 A B X X:控制信号 F=AX+BX X=1,F=A X=0,F=B
1
&
≥1
F
（2）电路（4位，右移，JK触发器构成）
X控制信号：X＝0，置数； X＝1，右移。 Dr右移数据输入端。 D3～D0并行数据输入端。
X控制信号：X＝0，左移，DL左移数据输入端。 X＝1，右移，Dr右移数据输入端；
双向移位寄存器示例，X控制信号：X＝0，左移， X＝1，右移，

第6章 时序逻辑电路

第6章 时序逻辑电路
n n Q1n+1 = Q2 Q3 1n Q n+1 Q2 = Q1n Q2n + Q1n Q3nQ2n n+1 n n Q3 = Q1nQ2 Q3n + Q2 Q3n
n n （3）输出方程 Y = Q2 Q3
2、列状态转换表 CP的顺序 0 1 2 3 4 5 6 7 0 1 现态 次态 0 0 0 1 1 1 0 0 0 0 0 1 1 0 0 1 0 0 0 0 1 0 1 0 1 0 0 1 0 1
Q1n 1 T1 Q1n X Q0n Q1n n Q0 T0 Q0n 1 Q0n Q0n
3
计算、列状态表
输入 X 0 0 0 0 1 1 1 1 现
n 1
态
n 0
次
态
输出
Q X Q Q n1 Q0 Q0n Y Q1nQ0nCP
5.2.1 同步时序逻辑电路的分析方法
基本步骤：
1.根据给定电路写出其时钟方程、输出方 程、驱动方程 2.求状态方程。
触发器输入信号的逻辑函数式
3.进行状态计算。把电路的输入和现态各种可能取值组 合代入状态方程和输出方程进行计算,得到相应的次态 和输出。 4.画状态图(或时序图)
时序电路分析过程示意图
X
& FF0 1T C1 Q0 FF 1 =1 1T C1 Q1
Y
例
“1”
CP
Q0
Q1
1
同步时序电路，时钟方程省去。 输出方程：
写 方 程 式
Y Q Q CP
n 1 n 0
T1 X Q0n 驱动方程： T0 1
2
求状态方程
T触发器的特性方程：

数字电子技术基础 第六章

数字电子技术基础 第六章

图6. 3.28
图6.3.27电路的时序图
常见的 异步二进制加法器产品有4位的（如74LS293、 74LS393、74HC393）等、7位的（如CC4024等）、12位的 （如74HC4040等）和14位的（如74HC4020等）几种类型。
2、异步十进制计数器
是在4位异步二进制加法计数器的基础上加以修改得到。 在计数过程中跳过从1010到1111这6个状态。

穆尔型：


状态机：State Machine简称SM。或称算法状态机 (Algorithmic State Machine，简称ASM)。
6.2 时序逻辑电路的分析方法

6.2.1 同步时序逻辑电路的分析方法 分析步骤：



1、从给定的逻辑图中写出每个触发器的驱动方程。 （存储电路中每个触发器输入信号的逻辑函数式）。 2、将得到的这些驱动方程代入相应触发器的特性方 程，得出每个触发器的状态方程，从而得到由这些状 态方程组成的整个时序电路的状态方程组。 3、根据逻辑图写出电路的输出方程。
图6. 3.38
例6.3.3电路的并行进位方式
图6. 3.39
例6.3.3电路的串行进位方式
例 6.3.4 P304
当M为大于N的素数时，不能分解成N1和N2，不能采用并行 进位方式和串行进位方式。必须采用整体置零方式或整体置 数方式。
图6. 3.40
例6.3.4电路的整体置零方式
整体置零方式： １、先将两片N进制计数器按最简单的方式接成一个大于M进制的计数器（如N*N进 制）。 ２、然后在计数器为M状态时译出异步置零信号，将两片N进制计数器同时置零。 整体置数方式： １、先将两片N进制计数器按最简单的方式接成一个大于M进制的计数器（如N*N进 制）。 ２、然后在选定的某状态下译出LD’=0信号，将两片N进制计数器同时置入适当数 值，获得Ｍ进制计数器。

数电 第6章时序电路

数电 第6章时序电路
' 2 ' 3 ' 1 ' 3 ' 0 ' (Q1Q0 )Q2 (Q3' (Q1Q0 )' )Q2
J2
* 1 ' 1 ' 0
K '2
' 1 ' 0
Q Q Q0 Q1Q Q0Q Q Q1
J1
* ' ' ' Q0 Q3' Q0 Q2 Q0 ' 3 ' 2 ' 0 '
' K1
0 0 1 1 0 1 1 0
0 1 0 1 0 1 0 1
0 1 1 0 1 0 0 0
1 0 1 0 1 0 1 0
6.4 同步时序逻辑电路的设计方法
逻辑电路设计:给定设计要求(或者是一段文字描叙,或 者是状态图),求满足要求的时序电路. 设计步骤:
1、进行逻辑抽象,建立电路的状态转换图(状态转换表)。 在状态表中未出现的状态将作为约束项 2、选择触发器,求时钟方程、输出方程和状态方程； 时钟:若采用同步方案,则CP1=CP2=CPn； 如果采用异步方案, 则需根据状态图先画出时序图,然后从翻转要求出发,为各个 触发器选择合适的时钟信号； 输出：输出与现态和输入的逻辑关系； 状态：各触发器的次态输出方程。
这三组方程反映的电路中各个变量 之间的逻辑关系。
3、进行计算:从输出方程和状态方程，不能看出电路 状态的变化情况。还需要转换成状态转换表和状态转 换图。
状态转换表：把任一组输入变量的值和电路的初态值代入状态 方程和输出方程，得到电路的次态和输出值；把得到的次态作 为新的初态，和现在的输入变量值再代入状态方程和输出方程， 得到电路新的次态和输出值。如此继续下去，把每次得到的结 果列成真值表的形式，得到状态转换表。

清华数字电路课件第六章-时序逻辑电路

清华数字电路课件第六章-时序逻辑电路

YF(Q)
仅取决于电路
6.2.时序逻辑电路的分析方法
6.2.1 同步时序逻辑电路的分析方法
时序逻辑电路的分析：就是给定时序电路，找出该的 逻辑功能，即找出在输入和CLK作用下，电路的次态和 输出。由于同步时序逻辑电路是在同一时钟作用下， 故分析比较简单些，只要写出电路的驱动方程、输出 方程和状态方程，根据状态方程得到电路的状态表或 状态转换图，就可以得出电路的逻辑功能。
6.2.时序逻辑电路的分析方法
(4）状态转换表：
Q Q12n n 1 1 D D12Q A1Q1Q2
A＝0时
Y [ A Q 1 ( Q 2 ) ( A Q 1 Q 2 ) ] A Q 1 Q 2 A Q 1 Q 2 A＝1时
Q2 Q1 Q2* Q1* Y
00 0 1 0 01 1 0 0 10 1 1 0 11 0 0 1
J3 Q1Q2,
K3 Q2
6.2.时序逻辑电路的分析方法
（2) 状态方程：
JK触发器的特性方程
Q *JQ KQ
将驱动方程代入JK触发器的特性方程中，得出电 路的状态方程，即
J1 (Q2Q3), K1 1
J2 Q1,
K2 (Q1Q3)
J3 Q1Q2,
K3 Q2
(3)输出方程：
QQ2*1*Q(1QQ22Q3)Q1QQ31Q2 Q3*Q1Q2Q3 Q2Q3
YQ2Q3
6.2.时序逻辑电路的分析方法
6.2.2时序逻辑电路的状态转换表、状态转换图、状态 机流程图和时序图
从例题可以看出，逻辑电路的三个方程应该说已 经清楚描述一个电路的逻辑功能，但却不能确定电路 具体用途，因此需要在时钟信号作用下将电路所有的 的状态转换全部列出来，则电路的功能一目了然

(完整word版)数字逻辑第六章

(完整word版)数字逻辑第六章

第六章时序逻辑电路1 ：构成一个五进制的计数器至少需要（）个触发器A：5B：4C：3D：2您选择的答案: 正确答案: C知识点：n个触发器可构成一个不大于2n进制的计数器。

A -————-————-——-——--——------——--——----——--———-——-—-———————--—-—————-——--————-—2 ：构成一个能存储五位二值代码的寄存器至少需要（）个触发器A:5B：4C:3D：2您选择的答案：正确答案： A知识点：一个触发器能储存1位二值代码,所以用n个触发器组成的寄存器能储存n位二值代码。

—-————-—---—---—-—-——--—-—-—----————---—---———--—---—--——---—-------—-——--——3 : 移位寄存器不具有的功能是（）A:数据存储B：数据运算C：构成计数器D:构成译码器您选择的答案: 正确答案: D知识点：移位寄存器不仅可以存储代码,还可以实现数据的串行—并行转换、数值的运算、数据处理及构成计数器。

-—-—————---—--——--—-——---——-———-—--—---——---————-————-----——-—--—-————--————4 ：下列说法不正确的是（）A:时序电路与组合电路具有不同的特点,因此其分析方法和设计方法也不同B:时序电路任意时刻的状态和输出均可表示为输入变量和电路原来状态的逻辑函数C:用包含输出与输入逻辑关系的函数式不可以完整地描述时序电路的逻辑功能D:用包含输出与输入逻辑关系的函数式可以完整地描述时序电路的逻辑功能您选择的答案：正确答案： D知识点：时序逻辑电路的逻辑关系需用三个方程即输出方程、驱动方程及状态方程来描述。

——---—-——-—————--—-——----—---—-—---—-——--—-—------————-——--——--———--—-------5 : 下列说法正确的是（ )A:时序逻辑电路某一时刻的电路状态仅取决于电路该时刻的输入信号B：时序逻辑电路某一时刻的电路状态仅取决于电路进入该时刻前所处的状态C:时序逻辑电路某一时刻的电路状态不仅取决于当时的输入信号,还取决于电路原来的状态D:时序逻辑电路通常包含组合电路和存储电路两个组成部分，其中组合电路是必不可少的您选择的答案: 正确答案： C知识点:时序逻辑电路的特点：时序逻辑电路中，任意时刻的输出不仅取决于该时刻的输入,还取决于电路原来的状态.时序逻辑电路通常包含组合电路和存储电路两个组成部分，其中存储电路是必不可少的。

数字电子技术 第6章 时序逻辑电路的设计

数字电子技术 第6章 时序逻辑电路的设计

17
2.画出次态状态表 画出次态状态表
次态 y=0(down) Q2 Q1 Q0 1 0 0 0 0 0 0 0 1 0 1 1 0 1 0 1 1 0 1 1 1 1 0 1 y=1(up) Q2 Q1 0 0 0 1 0 1 1 1 1 1 1 0 1 0 0 0 Q0 1 1 0 0 1 1 0 0
为使电路能自启动，将卡诺图中的最小项 xxx取做有效状态例如010状态，这时Q2n+1 的卡诺图应修改为右图。化简后得到新状 态方程： Q1n+1= Q2n⊕Q3n Q2n+1= Q1n+ Q2nQ3n Q3n+1= Q2n 驱动方程：J1=Q2n⊕Q3n 输出方程：C= Q1n Q2n Q3n K1=Q2n⊕Q3n J2=Q1n+Q3n K2=Q1n J3= Q2n K3= Q2n
检查自启动：设初态为000，来第1个CP脉冲，将跳变为010，进入循环状态，该电路可 以自启动。
11
6.3同步时序逻辑电路设计 同步时序逻辑电路设计 (时钟同步状态机的设计)
1.用状态图设计同步时序逻辑电路 ①状态序有规则的时序电路； ②态序不规则的Moore型； ③Mealy型 2. 使用状态表设计时序逻辑电路 3.使用状态转换表设计时序状态机
8
例2：设计一个串行数据检测器。要求连续输入3个或3个以 上的1时，输出为1，其它情况下输出为0。
(1)因为输入多于3个1，有输出。设输入变量为x；检测 (5)最多连续输入m=3，可选用 结果为输出变量，定义为y；又因连续输入3个1以上有 (7)逻辑电路图： n=2，2个J-K FF，于是可画出次 输出，因此要求同步计数。 态及输出卡诺图。还可分解为3 个卡诺图。 (2)状态分析：初态S0为全0状态，设输入一个1时为S1 态，输入2个1时为S2，输入3个1及以上为S3。 Q1n+1 Q0n+1 y (3)状态转换图如图所示： (4)状态转换表。因为输入m>3和连续输入3个1(m=3)状态是相同的，都停留在S2上，故 (8)检查能否自启动： 状态转换图可以简化成如下。 当电路初态进入11状态后： (6)状态方程：Q1n+1=xQ0Q1+xQ 若x=1时，Q1n+1Q0n+1=10状态为 1 sn S S1 S2 S 0 X 次态；若x=0时，Q1n+1 Q0n+1=00 3 n 驱动方程：J1=xQ0 J0=xQ1 0 S0/0 S0/0 S0/0 S0/0 次态。 输出方程：y=xQ1n 1 S1/0 该电路可以自启动。S2/0 S3/1 S4/1 Q0n+1=xQ1Q0+1Q1 K1=x K0=1 自启动部分
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

6 时序逻辑电路6.1.1 已知一时序电路的状态表如表题6.1.1所示，A为输入信号，试作出相应的状态图。

解：由状态图的概念及已知的状态表，可画出对应的状态图，如图题解6.1.1所示。

6.1.2已知状态表如表题6.1.2所示，输入为X1X0，试作出相应的状态图。

解：根据表题6.1.2所示的状态表，作出对应的状态图如图题解6.1.2所示。

6.1.3已知状态图如图题6.1.3所示，试列出它的状态表。

解：按图题6.1.3列出的状态表如表题解6.1.3所示。

6.1.5 图题6.1.5所示是某时序电路的状态图，设电路的初始状态为01，当序列A=100110（自左至右输入）时，求该电路输出Z的序列。

解：由图题6.1.5所示的状态图可知，当初态为01，输入信号的序列A=100110时，该时序电路将按图题解6.1.5所示的顺序改变状态，因而对应的输出序列为Z=011010。

6.1.6已知某时序电路的状态表如表题6.1.6所示，输入A，试画出它的状态图。

如果电路的初始状态在b，输入信号A一次是0、1、0、1、1、1、1，试求出其相应的输出。

解：根据表题6.1.6所示的状态表，可直接画出与其对应的状态图，如图题解6.1.6（a）当从初态b开始，依次输入0、1、0、1、1、1、1信号时，该时序电路将按图题解6.1.6（b）所示的顺序改变状态，因而其对应的输出为1、0、1、0、1、0、1。

6.2 同步时序逻辑电路的分析6.2.1 试分析图题6.2.1（a）所示时序电路，画出其状态表和状态图。

设电路的初始状态为0，试画出6.2.1（b）所示波形作用下，Q和Z的波形图。

解：由所给电路图可写出该电路的状态方程和输出方程，分别为1n nQ A Q Z AQ+=⊕=其状态表如表题解6.2.1所示，状态图如图题解6.2.1（a ）所示，Q 和Z 的波形图如图题解6.2.1（b ）所示。

6.2.2 试分析图题6.2.2（a ）所示时序电路，画出其状态表和状态图。

设电路的初始状态为0，画出在图题6.2.2（b ）所示波形作用下，Q 和Z 的波形图。

解：由所给电路可写出该电路的状态方程和输出方程1()()nn nnnnn n n n nQZQ ZQ AQ AQ Q AQ AQ Q AQ AQ AZ A Q+=+=+++=+==⊕其状态表如表题解6.2.2所示，状态图如图题解6.2.2（a ）所示，Q 和Z 的波形图如图题解6.2.2（b ）所示。

6.2.3试分析图题6.2.3所示时序电路，画出状态图。

解：由图题6.2.3所示电路写出其状态方程组和输出方程，分别为1101010n nn Q Q Q AZ AQ Q ++===其状态表如表题解6.2.3所示，状态图如图题解6.2.3所示。

6.2.4分析图题6.2.4所示电路，写出它的激励方程组、状态方程组和输出方程，画出状态表和状态图。

解：该电路的激励方程组为00111011J Q K AQ J Q K ====状态方程组为11011010110()nn n nnnnnn n QQ Q QQ Q AQ Q Q Q A ++==+=+输出方程为10ZAQ Q =根据状态方程组和输出方程可列出状态表，如表题解 6.2.4所示，状态图如图题解6.2.4所示。

6.2.5 分析图题6.2.5所示同步时序电路，写出各触发器的激励方程、电路的状态方程组和输出方程组，画出状态表和状态图。

解：由图题6.2.5所示电路可写出各触发器的激励方程为00110120121J A K AQ J AQ K A J AQ Q K ====== 该电路的状态方程组为1201211011011010100()()nn n n n n n n n n nnn n n n QA Q Q Q Q AQ Q AQ A Q Q QAQ AQ Q A Q Q +++==+=+=+=+ 输出方程为 2ZA Q =根据状态方程组和输出方程列出该电路的状态表，如表题解 6.2.5所示，状态图如图题解6.2.5所示。

6.2.6 试画出图题6.2.6（a ）所示时序电路的状态图，并画出对应于CP 的Q 1、Q 0和输出Z 的波形，设电路的初始状态为00。

解：该电路中的激励方程组为01011011J Q K J Q K ====状态方程组和输出方程分别为11101010nn n nn n Q Q Q QQ Q Z Q CP++===根据状态方程组和输出方程可列出该电路的状态表，如表题解6.2.6所示，状态图如图题解6.2.6（a ）所示。

图题解6.2.6（b ）所示是Q 1、Q 0及Z 的波形图。

6.3 同步时序逻辑电路的设计6.3.1 用JK触发器设计一同步时序电路，其状态如表题6.3.1所示。

解：所要设计的电路有4个状态，需要用两个JK触发器实现。

（1）列状态转换真值表和激励表由表题6.3.1所示的状态表和JK触发器的激励表，可列出转换真值表和对各触发器的激励信号，如表题解6.3.1所示、（2） 求激励方程组和输出方程由表题解6.3.1画出各触发器J 、K 端和电路输出端Y 的卡诺图，如图题解 6.3.1（a ）所示。

从而，得到化简得激励方程组。

001101J K J K A Q ====⊕和输出方程10Y Q Q =根据激励方程组和输出方程可画出电路图，如图题解6.3.1（b ）所示。

6.3.2 某同步时序电路的状态图如图题6.3.2所示，试写出用D触发器设计时的最简激励方程组。

解：由图题6.3.2所示状态图可知，实现该同步时序需要用三个D 触发器。

（1） 根据状态图列出完全的状态转换真值表，如表题解6.3.2所示。

其中，状态图中未包含的状态为不出现的状态，其次态可用无关项×表示。

（2）画出3个触发器的激励信号D 2、D 1、D 0的卡诺图。

由于D 触发器的特性方程为1n Q +=D,所以可由状态转换真值表直接画出这3个卡诺图，如图题解6.3.2所示。

（2） 由卡诺图得到最简激励方程组201201nn nD Q D Q D Q ===6.3.3 试用上升沿触发的JK 触发器设计一同步时序电路，其状态图如图题6.3.3所示，要求电路使用的门电路最少。

解：图题6.3.3所示的状态图有00、01、10、11四个状态，可用两个上升沿触发的JK触发器实现。

设两个触发器的输出为Q1、Q0,输入信号为A，输出信号为Y。

(1)根据图题6.3.3所示状态图和JK触发器的激励表，可直接列出相应的状态转换真值表和激励信号，如表题解6.3.3所示。

（2）画出激励信号的卡诺图，如图题解6.3.3（a）所示。

（3）由卡诺图得到最简激励方程组00101011J A Q K AQ J AQ K AQ ⎧==⎪⎨==⎪⎩和输出方程110Y AQ Q Q =+（4）根据激励方程组和输出方程画出逻辑电路图，如图题解6.3.3（b ）所示。

6.4 异步时序逻辑电路的分析6.4.1 一时序电路如图题6.4.1（a）所示，试画在CP作用下，Q0、Q1、Q2和Z端的波形，设各触发器的初态均为零。

解：图题6.4.1所示电路是异步时序电路。

（1）列出各逻辑方程组①根据逻辑图列出各触发器时钟信号的逻辑表达式 012CP CP CP Q ==⊕（当2Q =0时，对于每个CP 上升沿，011cp cp ==；当2Q =1时，对于每个CP 下降沿，011cp cp ==）2211(,1)CP Q Q cp ==对于上升沿②输出方程1Z Q =③激励方程组222101091111J Q K J Q K J Q K ⎧==⎪==⎨⎪==⎩④状态方程组12222222222221121111011111110200000000100()()()nn n n n nnn n n n n nnnn n n n Q J Q K Q cp Q cp Q cp Q cp Q J Q K Q cp Q cp Q Q cp Q cp QJ Q K Q cp Q cp Q Q cp Q cp +++=++=+=++=+=++=+（2）列出状态表，画出状态图根据状态方程组、输出方程及各触发器的CP 表达式可列出该电路的状态表，如表题解6.4.1所示。

具体推导方法如下：由于022cp cp CP Q ==⊕，所以当Q 2=0时，对应于每个CP 上升沿，021cp cp ==；当Q 2=1时，对应于每个CP 下降沿，021cp cp ==。

而cp 2对应于1Q 上升沿，即对应于Q 1由1变0时为1。

对表中的每一行，首先由10n n Q Q 推导出1110n n Q Q ++,然后根据Q 1是否从1跳变到0来确定cp 2是否为1，再决定12n Q +。

最后，根据1Q 决定Z 。

逐行类推，得到完全状态表。

然后根据表中状态的变化顺序，画出完全状态图，如图题解6.4.1Q，故写入圆圈内。

（a）所示。

由于输出Z值取决于1（3）画出波形图可按状态图的变化顺序，画出Q2、Q1、Q0和Z对应于图题6.4.1（b）所示CP的波形图，如图题解6.4.1（b）所示。

这里需要特别注意：因为CP0=CP1=CP⊕Q2，因此，要根据Q2的逻辑值正确确定状态变化所对应的CP脉冲沿。

6.4.2分析图题6.4.2所示时序电路[CP脉冲同图题6.4.1（b）]。

（1） 写出各触发器的CP 信号方程和激励方程。

（2） 写出电路的状态方程组和输出方程。

（3） 画出状态表及状态图。

（4） 画出电路的时序图。

解：（1）根据逻辑图写出各触发器的CP 信号表达式和激励方程组 ① 各触发器的时钟信号表达式CP 0=CP 1=CP (对于每个CP 上升沿，cp 0=cp 1=1) CP 2=Q 0 (对于Q 0上升沿，cp 2=1) ② 激励方程组001101211J Q K J Q Q K ====（2）写出电路的状态方程组和输出方程组 ①状态方程组122222222222211211110111121110200000000100()()()nn n n nnnnn n n n nnnnn n n n Q J Q K Q cp Q cp Q cp Q cp Q J Q K Q cp Q cp Q Q Q cp Q cp Q J Q K Q cp Q cp Q Q cp Q cp +++=++=+=++=+=++=+②输出方程 20ZQ Q =（3）列出状态表，画出状态图根据状态方程组、输出方程及各触发器始终信号cp n 可列出该电路的状态表，如表题解6.4.2所示。

具体方法如下：由于相应于每个CP 上升沿021cp cp ==，所以对表中的每一行，首先由210n n n Q Q Q 推导出1110n n Q Q ++，最后确定Z 。