当前位置：文档之家 › 材料加工冶金传输原理课件(吴树森

材料加工冶金传输原理课件(吴树森

  • 格式：ppt
  • 大小：2.68 MB
  • 文档页数：27

下载文档原格式

  / 27

合集下载

材料加工冶金传输原理完整(吴树森)ppt课件

材料加工冶金传输原理完整(吴树森)ppt课件


即
vx y
y0 0 .3 3 2 0 6 v
v x
即
0
vx y
y 0 0 . 3 3 2 v
v x
总 摩 阻 D : (b为 板 宽 )
L
D 0 d A b 0 d x 0 . 6 6 4 v b R e L
A
0
总 阻 力 系 数 :C d :
Cd
D
0
.5
v
2
A
1 .3 2 8
边界层理论的物理意义：
把绕流物体流动分为两个部分，即边界层的流动和势流流
动，主流区流动未受到固体壁面的影响，不发生切变，
故
这种无切变，不可压缩流体的流动称为势流。
4.1.2 边界层的流yx 态0
层流边界层：开始进入表面的一段距离，δ较 小，
流体的扰动不够发展，粘性力起主导作用。
17.05.2020 .
vy
vx y
1
P x
2vx y 2
平板表面边界层
Q
P y
0
又 势 流 区 vx
v,无 压 力 降 ,依
流 体 柏 努 利 方 程 ,故 有 平 板 表 面 P 0 x
17.05.2020 .
6
4.2.2 微分方程的解:
vx
vx x
vy
vx y
2v x y 2
vx vy 0 x y 布 拉 修 斯 对 上 方 程 组 引 入 流 函 数 ( x, y ),将 偏 微 分 方程化为可解的常微分方程
3
过渡区：随x的增大， δ也增大，惯性力作用 上升，层→湍转变为过渡区
湍流边界层：靠近平板表面，粘性力仍处于主导地位 （y=0,vx=0)有一定厚度的层流表层在湍流边界层内，距 离面板远处的流体，虽流速略小于vx,但已变得较大，并 为湍流，称其为湍流核心区。
材料加工冶金传输原理第五章(吴树森版)

材料加工冶金传输原理第五章(吴树森版)

第五章 边界层理论
5.1 边界层理论的基本概念 5.2 平面层流边界层微分方程 5.3 边界层内积分方程 5.4 平面绕流摩擦阻力计算
第五章 边界层理论
理论形成的背景：
实际流体流动无论是层流还是湍流，真正能够求得解析解的例子很少 ，主要是由于流体流动的控制方程是非线性的偏微分方程，处理该类方 程目前也是科学界的一大难题，但我们可以有近似的处理方法，方法之 一是在假设条件下获得简化的微分方程并用数值法求解，方法二是针对 湍流流动划分为边界层和中心区。 在实际工程中大多数问题是流体在固体限制的区域内的流动，远离固 体壁面区域的流体速度梯度很小，这样我们可以把远离边壁的大部分流 体处理为无粘性流体（基于速度梯度小，粘性力可忽略），用欧拉方程
这些边界条件是
1 ）y 0,x 0 2）y＞时,x 0 x 3）y＞时, 0 4）y 0, 0 y y
2 x 2
第五章 边界层理论
第五章 边界层理论
（5-19） 联立
（5-17）
第五章 边界层理论
湍流边界层内积分方程的解
第五章 边界层理论
第五章 边界层理论
m dy
x 0 x
l
M dy dy
2 x 0 x x 0 x
l
l
第五章 边界层理论
2）从CD面单位时间流出的动量记为 M
记为m x+Δx
x+Δx ，流出的质量
m
x x
d dy dy x dx
l l 0 x 0 x


[ ]
1
p 0 y
p dp x dx
p
2 v0
0
2
C
材料加工冶金传输原理课件(吴树森)

材料加工冶金传输原理课件(吴树森)


用翼栅及高温，化学， 用翼栅及高温，化学，多相流动理论成功设 计制造大型气轮机，水轮机， 计制造大型气轮机，水轮机，涡喷发动机等动力 机械， 机械，为人类提供单机达百万千瓦的强大动力 。
气轮机叶片
大型水利枢纽工程，超高层建筑， 大型水利枢纽工程，超高层建筑，大跨度桥 梁等的设计和建造离不开水力学和风工程。 梁等的设计和建造离不开水力学和风工程。
50～60年代又改进为船型，阻力系数为0.45。
80年代经风洞实验系统研究后，进一步改进为鱼 型，阻力系数为0.3。
后来又出现楔型，阻力系数为0.2。
90年代以后，科研人员研制开发了气动性能更优 良的未来型汽车，阻力系数仅为0.137。
90年代以后，科研人员研制开发了气动性能更优良 的未来型汽车，阻力系数仅为0.137。
虽然生活在流体环境中， 虽然生活在流体环境中，人们对一些 流体运动却缺乏认识，比如： 流体运动却缺乏认识，比如：
1. 高尔夫球 ：表面光滑还是粗糙？ 表面光滑还是粗糙？ 2. 汽车阻力： 来自前部还是后部？ 汽车阻力： 来自前部还是后部？ 3. 机翼升力 ：来自下部还是上部？ 来自下部还是上部？
高尔夫球运动起源于15世纪的苏格兰。
现在的高尔夫球表面有许多窝，在同样大小和重量下， 现在的高尔夫球表面有许多窝，在同样大小和重量下， 飞行距离为光滑球的5倍 飞行距离为光滑球的 倍。
光滑的球和非光滑球对比
汽车发明于19世纪末 世纪末。 汽车阻力 汽车发明于 世纪末。
当时人们认为汽车高速前进时的阻力主要来自车前部 对空气的撞击。 对空气的撞击。
此后， 此后，流体力学的发展主要经历了三个阶段：
１.伯努利所提出的液体运动的能量估计及欧拉 所提出的液体运动的能量估计及欧拉 所提出的液体运动的解析方法， 所提出的液体运动的解析方法，为研究液体运 动的规律奠定了理论基础， 动的规律奠定了理论基础，从而在此基础上形 成了一门属于数学的古典“水动力学” 成了一门属于数学的古典“水动力学”（或古 流体力学” 典“流体力学”）。
材料加工冶金传输原理习题答案(吴树森版)

材料加工冶金传输原理习题答案(吴树森版)

第一章流体的主要物理性质1-1何谓流体，流体具有哪些物理性质？答：流体是指没有固定的形状、易於流动的物质。

它包括液体和气体。

流体的主要物理性质有：密度、重度、比体积压缩性和膨胀性。

2、在图所示的虹吸管中，已知 H1=2m , H2=6m ，管径D=15mm ，如果不计损失，问 S 处的压强应为多大 时此管才能吸水？此时管内流速u 2及流量Q 各为若干？(注意：管B 端并未接触水面或探入水中)解：选取过水断面 1-1、2-2及水准基准面 O-O ，列1-1面(水面)到2-2面的贝努利方程再选取水准基准面 O' -O',列过水断面2-2及3-3的贝努利方程(B) 因V2=V3 由式(B)得(P 1 P 2)用U 形管中液柱表示，所以 Q A 2)2gh(A)—(0.1)2 ；2 9.81 °.2 (13.552103 1 103)0.074 (m 3/s)[1 (A 2)2]4103 (1 (CL)2)&10.15式中 、——被测流体和U 形管中流体的密度如图6-3 17(a)所示，为一连接水泵出口的压力水管，直径 d=500mm 弯管与水准的夹角 45° ,水流流过 弯管时有一水准推力，为了防止弯管发生位移，筑一混凝土镇墩使管道固定。

若通过管道的流量s,断面1-1和2-2中心点的压力 P1相对=108000N/肝，P2相对=105000N/肝。

试求作用在镇墩上的力。

［解］如图6 3 17(b)所示，取弯管前彳爰断面 1 — 1和2-2流体为分离体，现分析分离体上外力和动量变化5、有一文特利管(如下图)，已知d 1 15cm, d 2=10cm,水银差压偏亦E 若不计阻力损失，求常温(20 C)下,通过文氏管的水0最1 * I解：在喉部入口前的直管截面1和喉部截面2处测量跚力另2P —const 可建立有关此截面的伯努利方程: 22V 1 2侦 P 22根据连续性方程，截面1和2上的截面积A I 和A 2与流体流速V I 和V 2的关系式为二二二所以V 22( P 1 P 2) A 2 2,° (J图也丁吸管 C/ 、通过管子的流体流量为 Q A 2(P1 P 2)［1 (A 2)2】iA 1设管壁对流体的作用力 R,动量方程在x 轴的投影为:动量方程在x 轴的投影为：镇墩对流体作用力的合力 R 的大小及方向为:流体对镇墩的作用力 P 与R 的大小相等方向相反。

材料加工冶金传输原理习题答案(吴树森版)

材料加工冶金传输原理习题答案(吴树森版)

第一章 流体的主要物理性质1-1谓流体，流体具有哪些物理性质？答：流体是指没有固定的形状、易于流动的物质。

它包括液体和气体。

流体的主要物理性质有：密度、重度、比体积压缩性和膨胀性。

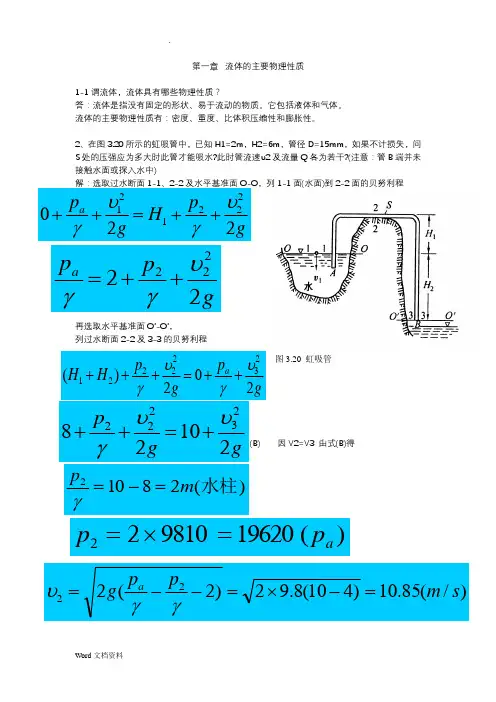
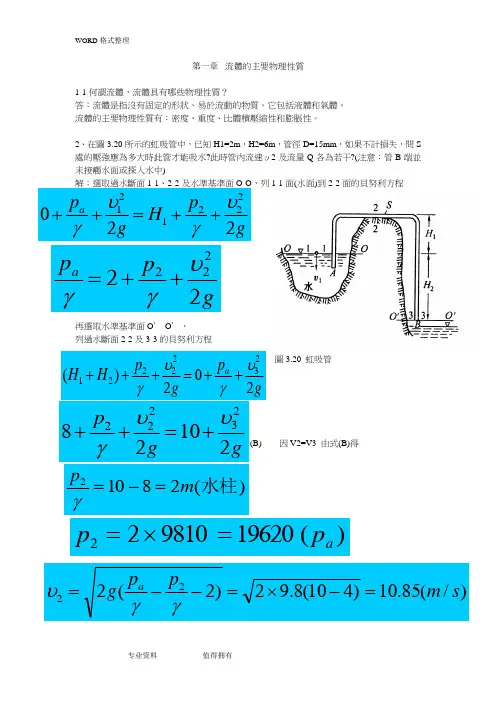
2、在图3.20所示的虹吸管中，已知H1=2m ，H2=6m ，管径D=15mm ，如果不计损失，问S 处的压强应为多大时此管才能吸水?此时管流速υ2及流量Q 各为若干?(注意：管B 端并未接触水面或探入水中)解：选取过水断面1-1、2-2及水平基准面O-O ，列1-1面(水面)到2-2面的贝努利程再选取水平基准面O ’-O ’，列过水断面2-2及3-3的贝努利程(B) 因V2=V3 由式(B)得 图3.20 虹吸管gpH gpa 220222121υγυγ++=++gppa 22222υγγ++=gp g p H H a 202)(2322221υγυγ++=+++ggp2102823222υυγ+=++)(28102水柱m p=-=γ)(19620981022a p p =⨯=)/(85.10)410(8.92)2(222s m ppg a =-⨯=--=γγυ)/(9.1)/(0019.085.104)015.0(3222s L s m A Q ==⨯⨯==πυ5、有一文特利管(如下图)，已知d 1 =15cm ，d 2=10cm ，水银差压计液面高差∆h =20cm 。

若不计阻力损失，求常温(20℃)下，通过文氏管的水的流量。

解：在喉部入口前的直管截面1和喉部截面2处测量静压力差p 1和p 2，则由式const v p=+22ρ可建立有关此截面的伯努利程： ρρ22212122p v p v +=+ 根据连续性程，截面1和2上的截面积A 1和A 2与流体流速v 1和v 2的关系式为2211v A v A =所以 ])(1[)(2212212A A p p v --=ρ 通过管子的流体流量为 ])(1[)(2212212A A p p A Q --=ρ )(21p p -用U 形管中液柱表示，所以074.0))15.01.0(1(10)1011055.13(2.081.92)1.0(4])(1[)(22223332212'2=-⨯⨯-⨯⨯⨯⨯=--∆=πρρρA A h g A Q (m 3/s)式中 ρ、'ρ——被测流体和U 形管中流体的密度。

材料加工冶金传输原理课件(吴树森概要

材料加工冶金传输原理课件(吴树森概要


Pa
2018/10/14
4
第一章 动量传输的基本概念
1、 1 流体及连续介质模型 在剪切应力的作用下会发生 连续的变形的物质。
1、流体的定义:
流体的密度
m lin v 0 V
ΔV 从宏观上看应足够小， 而从微观上看应足够大。
2018/10/14
5
1.1 流体的概念及连续介质模型
2018/10/14
27
Fn Fτ
F
2018/10/14
22
流体的静压力及其特点： 2. 流体中任意点上的静压力在各方向上均相等而 与方向无关。 证明：在静止的流体中取一无限小的三角形，(如 图所示）它包含有P点。三角体的厚度取单位厚 度，现分析其受力的情况，先考虑X方向的力： dz=1 y
dy
Pθ dx 2 dy 2
P2 2 1 P1
2 1
P1 P2
2、 等压时（P1=P2）
2
T1 1 T2
T0 0 t 0 Tt 1 t
β=1/273
11
2 1
2018/10/14
T2 T1
流体的基本性质 当气体的压力不太高（<10kPa) ,或速度不太高 (<70m/s)时，可认为是不可压缩的。 3、绝热时 当气体没有摩擦，又没有热交换时， 可认为是绝热可逆过程 ：
第一篇
动量的传输
概述 冶金过程：是物理化学过程、动量、热量、质 量传输过程的组合过程。 传输理论的基础：质量守恒定律；动量守恒定 律；能量守恒定律。 研究的目的：研究速率过程（动量、热量、质 量） 本学科的现状与发展
2018/10/14
2
工程单位制 ； 基本单位：长度，时间，力 一 单位制： 国际单位制；基本单位：长度，时间，质量 工程单位制规定：质量为1kg的物体在标准重力加速度处所 受的引力为1kg力。 缺点g 随地点的不同而异，力不能作为基本单位，且kg Kgf是不同的概念。 国际单位制： 基本单位： 米（m） 公斤（kg）秒（s）度（℃）（K） 导出单位：力—牛顿（1N=1kg×m/S） 能量——焦耳（1J=1kg· ㎡/S² ） 压力（强）——帕斯卡（Pa=N/㎡） 功率——瓦（W=J/s）
材料加工冶金传输原理第十章(吴树森版)

材料加工冶金传输原理第十章(吴树森版)


(1)
式中，定性温度Tf可取 ' " T f (T f T f ) 2 式中，Tf'、Tf" — —管道进、出口流体温度。
( 2)流体粘性系数 f 不宜过大 : f ≯ 2 水
(1)温差(TW Tf )不宜过大 : 空气 ≯ 50℃; 水 ≯ 20 ~ 30℃; 油 ≯ 10℃.
• （1）努塞尔准数Nu
– 将其变形为
其物理意义可理解为流体的导热热阻和其对流热阻的比 值，它反映了给定流场的对流换热能力与其导热能力的 对比关系，其大小反映了对流传热能力的大小。由于式 中包含有待定的物理量α ，故Nu是被决定性准数。
10.3 对流换热的准数方程式
• （2）傅里叶数Fo 将其变形为
物理意义可理解为流体的单位体积物体的导热 速率与单位体积物体的蓄热速率比值，Fo越大， 温度场越趋于稳定。
10.3 对流换热的准数方程式
• （3）物性准数Pr 将其变形为
物理意义可理解为流体动量传输能力与热量传 输能力之比。从边界层概念出发，可以认为是 动力边界层与热边界层的相对厚度指标。
10.3 对流换热的准数方程式
T T T T 2T 2T 2T vx vy vz a( 2 ) 2 2 t x y z x y z
10.3 对流换热的准数方程式
10.3 对流换热的准数方程式
10.3 对流换热的准数方程式
10.3 对流换热的准数方程式
10.3 对流换热的准数方程式
能量微分方程方程 v x
动量微分方程 连续性方程
T T 2T vy a x y y 2
v x v x 2vx vx vy x y y 2
v x v y 0 x y
第八章 冶金传输原理热量传输

第八章 冶金传输原理热量传输


第一章 绪论
• 研究目的： 一定条件下热量传递的速率。 提高传热速率：提高生产率
降低传热速率：提高热效率，减少热损失，节能
传热学与工程热力学的异同
铁块，M1 300oC
热力学：tm , Q 传热学：过程的速率
水，M2 20oC
5.1 热量传输的基本方式
传热方式 传导传热 （导热） 对流传热 （对流） 辐射传热 （辐射）
• What if coils were at the bottom?
1. 定义与特征 • 热对流：流体中（气体或液体）温度不同 的各部分之间，由于发生相对的宏观运动 而把热量由一处传递到另一处的现象。 流体中有温差 — 热对流必然同时伴随着 热传导，自然界不存在单一的热对流 • 对流换热：流体流过与之温度不同的固体 壁面时的热量交换。 Convection heat transfer
三、热辐射（Thermal radiation） 1.定义 ——物体通过电磁波来传递热量的方式。 电磁波：在真空中可以传输 30km/s
物体的温度越高、辐射能力越 强；若物体的种 类不同、表面 状况不同，其辐射能力不同
辐射换热：物体间靠热辐射进行的热量 传递 Radiation heat transfer
热量传输的基本概念
南昌大学 机电工程学院 王文琴
参考书
• 《材料加工冶金传输原理》的“热量传输部分” 吴树森 编著 • 《冶金传输原理》的“热量传输部分” 沈颐身等 编著 • 《传热学》 杨世铭 陶文铨 编著 • 《HEAT TRANSFER》Yanhui Feng等编著 • 《Transport Phenomena》R.Byron Bird编著
解： 根据傅立叶导热公式，对于纯铜板，
q1 1
材料加工冶金传输原理第九章(吴树森版)

材料加工冶金传输原理第九章(吴树森版)


第九章 导热
• 稳定阶段
是指导热体经过无限长时间后导热体内、外达到新 的稳定状态。
三个阶段中，本章仅研究正规阶段内热量传递规律。
研究此类问题的任务是：
1）确定被加热或被冷却物体内部某点达到预定温度 所需经历的时间，以及该期间所供给或放出的热量。 2）经过一定时间后物体内某点的温度。 3）物体内部最大温差及其所产生的热应力和热变形 是否会造成安全问题。
第九章 导热
温度场分离变量
带入式（9-29），则
将上式分离变量得
第九章 导热
第九章 导热
考虑边界条件 当x=0时，X必须为0，因此C1=0
第九章 导热
当Y=∞时，Y必须为0，因此C3=0 于是
故乘积解为
当Y=0时，Y必须为T0，因此
第九章 导热
第九章 导热
5 一维非稳态导热
非稳态导热的基本概念 不稳态导热的特点 （1）物体内温度随时间变化； （2） 不同位置达到指定温度的实际不同； （3） 热量随时间而变化。 一大平板，突然放入加热炉中加热，平板受 炉内烟气环境的加热作用伴随着热流向平板 中心的传递，其温度就会从平板表面向平板 中心随时间逐渐升高，其内能也逐渐增加， 右图显示了大平板加热过程中温度 总之，在非稳态导热过程中物体内的温度和热流都是在不断的变化，而且是一 个不断地从非稳态到稳态的导热过程，也是一个能量从不平衡到平衡的过程。
第九章 导热
采用了过余温度，半个平板厚度适用的微分方程及定解条件 可表示为
第九章 导热
第九章 导热
w tf t w f ( Bi, Fo ) 0 tf t0
x δ
表面上的过余温度 壁中心过余温度
任意点x的过余温度
m tf t m f ( Bi, Fo ) 0 tf t0
材料加工冶金传输原理最新版精品课件传热部分-第二章 一维稳态导热

材料加工冶金传输原理最新版精品课件传热部分-第二章 一维稳态导热

第二章稳态导热过程分析§2-1 导热的基本概念§2-2 典型几何体的一维稳态导热§2-3 变截面一维稳态导热§2-4 有内热源的稳态导热本章学习目标与要求1.着重掌握傅立叶定律及其应用。

2.掌握导热系数的影响因素。

3.了解导热问题的数学描写（导热微分方程及定解条件）4.能够应用傅立叶定律对几种典型几何形状物体的一维稳态导热问题进行分析和计算。

第一节导热的基本概念一、温度场和温度梯度二、傅立叶定律三、导热微分方程一、温度场和温度梯度2.等温线（面）：同一瞬间温度场中温度相同的点连成的线（面）称为等温线（面）。

等温线（面）有如下特点：①不可能相交；②对连续介质，等温线（面）只可能在物体边界中断或完全封闭；③沿等温线（面）无热量传递；④由等温线（面）的疏密可直观反映出不同区域温度梯度（或热流密度）的相对大小。

tt-Δt t+Δt为热流密度，指单位时间通过单位面积的表示热量传递指向温度降低的方向；是通过该点的等温线上法向单位矢量，指xt qx∂∂−=λyt qy∂∂−=λt∂2.导热系数•傅立叶定律给出了导热系数的定义:单位温度梯度下物体内所产生的热流密度。

gradt q /−=λ[W/（m·℃）]•它表示物体导热本领的大小。

•导热系数的影响因素：是物性参数。

——物质结构：物质的种类、材料成分；——物质的状态：温度、湿度、压力、密度等。

)1(0bT +=λλ保温材料（绝热材料）3.定解条件•完整数学描述：导热微分方程+ 单值性条件•单值性条件：确定唯一解的附加补充说明条件，包括几何、物理、初始、边界四项③初始条件：又称时间条件，反映导热系统的初始状态；①几何条件：说明导热体的几何形状和大小，如：平壁或圆筒壁；厚度、直径等；②物理条件：说明导热体的物理特征，如物性参数λ、c 和ρ的数值，是否随温度变化；有无内热源、大小和分布；④边界条件：反映导热系统在界面上的特征，也可理解为系统与外界环境之间的关系。

材料加工冶金传输原理习题答案解析(吴树森版)

材料加工冶金传输原理习题答案解析(吴树森版)


解：以下出口為基準面，不計損失，建立上出口和下出口面伯努
利方程： h Pa v12 0 Pa v22
2g
2g
代入數據得：v2=6.52m/s
由 v1A1 v2 A2 得:d2=5.3cm
3.6 水箱側壁接出一直徑 D＝0.15m 的管
路，如圖 3.29 所示。已知 h1＝2.1m，
h2=3.0m,不計任何損失，求下列兩種情況下
P2 P1 g(h1 h2 ) 4900 (Pa)
P3 P1 g(h3 h1) 1960 (Pa)
专业资料
值得拥有
WORD 格式整理
P4 P3 1960 (Pa)
P5
P4
g(h5
h4 )
76F4d34(2Pa
gh )
F2 D
2
2
2
2-6 兩個容器 A、B 充滿水，高度差為 a0 為測量它 們之間的壓強差，用頂部充滿油的倒 U 形管將兩 容器相連，如圖 2.24 所示。已知油的密度ρ油 =900kg／m3，h＝0.1m，a＝0.1m。求兩容器中的 壓強差。 解：記 AB 中心高度差為 a，連接器油面高度差為 h，B 球中心與油面高度差為 b；由流體靜 力學公式知：
l yc
Jc h0 d 1 ycA sin 45 2 sin 45 a
a3b 4 h0
0.44 ab
sin 45
X=d=0.6m,由理論力學平衡理論知，當閘門剛剛轉動時，力 F 和 T 對鉸鏈的力矩代數和為零， 即：
M Fl Tx 0
故 T=6609.5N
2-14 有如圖 2.32 所示的曲管 AOB。OB 段長 L1＝0.3m，∠AOB=45°， AO 垂直放置，B 端封閉，管中盛水，其液面到 O 點的距離 L2＝0.23m， 此管繞 AO 軸旋轉。問轉速為多少時，B 點的壓強與 O 點的壓強相 同?OB 段中最低的壓強是多少?位於何處? 解：盛有液體的圓筒形容器繞其中心軸以等角速度 ω 旋轉時，其管內 相對靜止液體壓強分佈為：

材料加工冶金传输原理第八章(吴树森版)


• What if coils were at the bottom?
1. 定义与特征 • 热对流：流体中（气体或液体）温度不同 的各部分之间，由于发生相对的宏观运动 而把热量由一处传递到另一处的现象。 流体中有温差 — 热对流必然同时伴随着 热传导，自然界不存在单一的热对流 • 对流换热：流体流过与之温度不同的固体 壁面时的热量交换。 Convection heat transfer
傅里叶定律表达式：
8.2 温度场、等温面和温度梯度
8.3热导率与热扩散率
热导率（导热系数）(Thermal conductivity)
q T n n
λ—— 具有单位温度差（1K）的单位厚度的物体 (1m)，在它的单位面积上(1m2)、每单位时间(1s) 的导热量(J)
热导率表示材料导热能力大小；物性参数；实验确定
四傅里叶定律: 1822年，法国数学家Fourier
t
（8-1）
Q
tw1 Q
tw2
x
（8-2）
图1－1通过无限大平板的导热
一维稳态导热傅里叶定律的数学表达式
热导率(导热系数) Thermal conductivity
让· 巴普蒂斯· 约瑟夫· 傅立叶 (Jean Baptiste Joseph Fourier， 1768 –1830)，法国著名数学家、 物理学家，1817年当选为科学 院院士，1822年任该院终身秘 书，后又任法兰西学院终身秘 书和理工科大学校务委员会主 席，主要贡献是在研究热的传 播时创立了一套数学理论。
降低传热速率：提高热效率，减少热损失，节能
传热学与工程热力学的异同
铁块，M1 300oC
热力学：tm , Q 传热学：过程的速率

材料加工冶金传输原理最新版精品课件传热部分-第三章 非稳态导热

第三章非稳态导热本章学习目标及要求1. 掌握非稳态导热的特点；2. 掌握集总参数法的基本原理及其应用；3. 了解一维非稳态导热问题的分析解求解方法及解的形式；4. 掌握一维非稳态导热的诺模图求解方法。

本章学习重难点1. 非稳态导热过程的基本概念与特点；2. 零维非稳态导热的集总参数法；3. 一维非稳态导热的分析解求解方法；4. 一维非稳态导热的诺模图求解方法。

第一节非稳态导热过程1.非稳态导热的定义•物体的温度随时间而变化的导热过程称为非稳态导热。

许多工程实际问题都牵涉到非稳态导热过程，如动力机械的启动、停机、变工况运行，热加工、热处理过程等。

()z y x=ft,,,τ2.非稳态导热过程的分类¾周期性非稳态在周期性变化边界条件下发生的导热过程，如：①地表层、房屋建筑墙壁的导热过程；②内燃机气缸壁的导热。

¾非周期性非稳态导热通常是在瞬间变化的边界条件下发生的导热过程，如：①热处理工件的加热或冷却等；②一般物体的温度随时间的推移逐渐趋近于恒定值。

3.非稳态传热过程的特点（1）过程温度变化特性(a)τ= τ1(b)τ= τ2(c)τ= τ3(d)τ= τ4①初始阶段：温度变化到达右壁面之前(如曲线A-C-D)，右侧不参与换热，此时物体内分为两个区间，非稳态导热规律控制区A-C和初始温度区C-D。

②正规状况阶段：温度变化到达右壁面之后，右侧参与换热，初始温度分布的影响逐渐消失。

τ= τ3：穿透时间a ∂∂(木材 1.5×10-7银2×10-4钢 1.25×10-5黄铜 3.4×10-5第二节集总参数法•(1) 为什么要等5分钟才能取出？•(2) 体温计读数是否为人体温度？误差有多大？引题: 用体温计测量病人体温有没有简化方法可以将偏微分方程变成常微分方程？1. 非稳态导热的三种情形Bi<<1：内部导热热阻远小于外部对流换热热阻，从曲线上看，物体内部的温度几乎是均匀的。

材料加工冶金传输原理第三章(吴树森版)

d2
d1
d3
第二节 连续性方程
解：1）根据连续性方程 Q=V1A1=V2A2=V3A3，则 V1=Q/A1=8.16m/s， V2=V1A1/A2=2.04m/s， V3=V1A1/A3=0.51m/s
d2 d1
d3
2) 各断面流速比例保持不变， Q=8L/s,即流量增加为2倍， 则各断面流速亦加至2倍。即
（3 - 12）
第二节 连续性方程
由：质量输入输出差=累积 → 式（3-11）=（3-12）
( v x ) ( v y ) ( v z ) dxdydzdt dxdydzdt y z t x
对单位时间、单位空间，有：
( v x ) ( v y ) ( v z ) 0 t x y z (3 - 13) 流体的连续性方程
流量与平均速度 流量——单位时间流过有效断面的流体的量
流束的流量
dQ=vdA
流管的流量
Q
A vdA
v
v dA vdA Q
A
A
AvdA A dA
Q A
(3 9)
第二节 连续性方程
流体为连续介质，在研究流体运动时，同样认为流 体是连续地充满它所占据的空间。根据质量守恒定律， 对于空间固定的封闭曲面，稳定流时流入的流体质量 必然等于流出的流体质量；非稳定流时流入与流出的 流体质量之差，应等于封闭曲面内流体质量的变化量。 连续性方程就是反映这个原理的数学关系。
d
dt dx dy dz t x y z
d vx vy vz dt t x y z
将式（b)代入式（a),方程两边同除以ρ，得：
v y v x v z 0 dt x y z 1 d

材料加工冶金传输原理习题答案(吴树森版)

材料加工冶金传输原理习题答案(吴树森版)第一章 流体的主要物理性质1-1何谓流体，流体具有哪些物理性质？答：流体是指没有固定的形状、易于流动的物质。

它包括液体和气体。

流体的主要物理性质有：密度、重度、比体积压缩性和膨胀性。

2、在图3.20所示的虹吸管中，已知H1=2m ，H2=6m ，管径D=15mm ，如果不计损失，问S 处的压强应为多大时此管才能吸水?此时管内流速υ2及流量Q 各为若干?(注意：管B 端并未接触水面或探入水中) 解：选取过水断面1-1、2-2及水平基准面O-O ，列1-1面(水面)到2-2面的贝努利方程再选取水平基准面O ’-O ’，列过水断面2-2及3-3的贝努利方程(B) 因V2=V3 由式(B)得图3.20 虹吸管gp H g p a 220222121υγυγ++=++gp p a22222υγγ++=gp g p H H a 202)(2322221υγυγ++=+++gg p 2102823222υυγ+=++)(19620981022a p p =⨯=5、有一文特利管(如下图)，已知d1=15cm，d2=10cm，水银差压计液面高差∆h =20cm。

若不计阻力损失，求常温(20℃)下，通过文氏管的水的流量。

解：在喉部入口前的直管截面1和喉部截面2处测量静压力差p1和p2，则由式constvp=+22ρ可建立有关此截面的伯努利方程：ρρ22212122pvpv+=+根据连续性方程，截面1和2上的截面积A1和A2与流体流速v1和v2的关系式为2211vAvA=所以])(1[)(2212212AAppv--=ρ通过管子的流体流量为])(1[)(2212212AAppAQ--=ρ)(21pp-用U形管中液柱表示，所以074.0))15.01.0(1(10)1011055.13(2.081.92)1.0(4])(1[)(22223332212'2=-⨯⨯-⨯⨯⨯⨯=--∆=πρρρAAhgAQ(m3/s)式中ρ、'ρ——被测流体和U形管中流体的密度。

材料加工冶金传输原理课件(吴树森

2 t d 2t a 2 0 t 仅是 x的函数 0 2 x dx

∴导热微分方程为：
边界条件为： x =0，t= tw1 ； x=， t = tw2 上述微分方程是一二阶线性常微分方程，积分二次 得：
2013-7-25 4
t c1 x c2


式中： c1 、 c2 为积分常数，由边界条件（B· C） 确定。 将B· C代入得：
2013-7-25
8
•二 , 多层平壁的导热
工程中许多平壁并不是由单一的材料组成的而是 由多种材料组成的复合平壁.如工业炉中的炉墙就是由 耐火砖、绝热砖、金属护板等不同的材料组成的多层 平壁,由于各层平壁的的不同，它们的热阻亦是不同 的. 其求解方法可利用单层平壁的结果,即一维稳态时 通过各层平壁的热通量(热流量)处处相等. 如果通过第一层的热量大于第二层的热量,说明第 一层就有了热量的积蓄,其温度就会升高,而这是一个 非稳态传热,这与假定条件不符. 考虑如图所示由三层材料组成的无限大平壁,假定 个层面接触良好,接触面上具有均匀的温度,各层的温 度及厚度如图所示.
22

联立解得：
C1 t f 2 - t f1 1 1 h h 2 1
C2 t f 1 t f 2 - t f1 1 1 h1 h h 2 1

将积分常数代入式（10－46）即得温度分布：
1 x t f 2 - t f 1 t h 1 1 1 h1 h2 t f1
13
2013-7-25
讨论：

1. 关于夹层温度
在计算中我们仍假定了材料的导热系数为常数并 取其平均温度下的导热系数，而实际问题中知道的是 多层平壁的两个外表面温度，其它的温度并不知道， 即界面温度为未知，各层的导热系数又是温度的函数。 此时仅用上式计算是不够的，现一般是用试算法，是 一种逐步逼近得计算法。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一篇
动量的传输
概述 冶金过程：是物理化学过程、动量、热量、质 冶金过程：是物理化学过程、动量、热量、 量传输过程的组合过程。 量传输过程的组合过程。 传输理论的基础：质量守恒定律； 传输理论的基础：质量守恒定律；动量守恒定 能量守恒定律。 律；能量守恒定律。 研究的目的：研究速率过程（动量、热量、 研究的目的：研究速率过程（动量、热量、质 量） 本学科的现状与发展
τ=0
τ
=∆τ y
x
2011-12-18
无滑移边界条件实验
A
13
流体的粘性
实验二 两平行平板，中间充满流体，平板的面积为A， 两平行平板，中间充满流体，平板的面积为 ，其间 的流体均匀，高为H。 的流体均匀，高为 。 且H ≪ A ½ 叫无限大平板
固定
y
vx（y）
H 稳定 开始 x
v0
2011-12-18
2011-12-18
5
1.1
流体的概念及连续介质模 型
1.1.2 连续介质模型 连续介质—把流体视为充满其占有空间、 连续介质 把流体视为充满其占有空间、由大量的没有间隙存 把流体视为充满其占有空间 在的流体质点所组成的连续介质。 流体质点所组成的连续介质 在的流体质点所组成的连续介质。 只研究宏观性质，不研究微观性质。 只研究宏观性质，不研究微观性质。 注：①只适用于宏观情况，假设取微单元时，仍为连续。 只适用于宏观情况，假设取微单元时，仍为连续。 ②各种物理量是空间和时间的连续函数。 各种物理量是空间和时间的连续函数。
2011-12-18
4
第一章 动量传输的基本概念
1、1 、 流体及连续介质模型 在剪切应力的作用下会发生 连续的变形的物质。 连续的变形的物质。 1、流体的定义: 、流体的定义
流体的密度
ρ
∆ m = lin ∆ → ∆ v 0 V
∆V 从宏观上看应足够小， 从宏观上看应足够小， 而从微观上看应足够大。 而从微观上看应足够大。
14
F
流体的粘性
将下面的一块平板作匀速直线运动， 将下面的一块平板作匀速直线运动，连续测定使这块 平板作匀速直线运动所需的力。实验测得稳定后F=Const。 平板作匀速直线运动所需的力。实验测得稳定后 。 实验结果： 实验结果： 1 0与F不变时，F ∝A 不变时， 不变时 2v A=Const 时：F ∝ o /H （唯一的单增函数） 唯一的单增函数） 结果的表达式为： 结果的表达式为： v
dvx F = ±µ A dy
τ yx
F dvx = = ±µ A dy
τyx下标：x为运动方向；y为在该方向上有速度梯度 下标： 为运动方向 为运动方向； 为在该方向上有速度梯度 式中： 流体的动力粘度系数， 式中：µ 流体的动力粘度系数，其单位为 Pa ·S 1Pa ·S=1N ·S/ ㎡ =1Kg/ms
2011-12-18
2
基本单位：长度，时间， 工程单位制 ； 基本单位：长度，时间，力 单位制： 一 单位制： 国际单位制；基本单位：长度，时间， 国际单位制；基本单位：长度，时间，质量 工程单位制规定 质量为1kg的物体在标准重力加速度处所 规定： 工程单位制规定：质量为 的物体在标准重力加速度处所 受的引力为1kg力。 受的引力为 力 缺点g 随地点的不同而异，力不能作为基本单位， 缺点g 随地点的不同而异，力不能作为基本单位，且kg Kgf是不同的概念。 是不同的概念。 是不同的概念 国际单位制： 国际单位制： 基本单位： ）（K） 基本单位： 米（m） 公斤（kg）秒（s）度（℃）（ ） ） 公斤（ ） ） 导出单位： 牛顿（ 导出单位：力—牛顿（1N=1kg×m/S） 牛顿 × ） 能量——焦耳（1J=1kg·㎡/S²） 焦耳（ 能量 焦耳 ㎡ ） 压力（ 帕斯卡（ 压力（强）——帕斯卡（Pa=N/㎡） 帕斯卡 ㎡ 功率——瓦（W=J/s） 功率 瓦 ）
2011-12-18
3
单位换算： 二 单位换算： 1N=0.102kgf 力 : 1kgf=9.807 N 压力（ Pa 压力（强）:1atm=1.01325×105 × 1atm=760mmHg=10332mmH2O 1at=10000mmH2O=735.6mmHg=9.807×104 Pa × 1mmH2O=1kgf/㎡=9.8Pa ㎡ 能量: 1kcal=4.187kJ 能量 1kJ=0.239kcal 1w=1J/s=0.86kcal/h 1kcal/h=1.163w
2011-12-18
6
流体及连续介质模型 流体的密度
∆m ∆v
ρ v
对于均质流体
∆v
ρ
2011-12-18
m = V
7
流体及连续介质模型 1、2 流体的主要物理性质 、 流体的密度 只有当流体是连续介质时， 只有当流体是连续介质时，流体的一切物理属 性均可以看作是坐标和时间的连续函数。 性均可以看作是坐标和时间的连续函数。可以用 微积分来处理问题。 微积分来处理问题。 流体的比容 1 V υ= = ρ m 即密度的倒数。 即密度的倒数。
1 滨海姆流体 d v τ =τ0 + µ
2011-12牛顿流体 当
d v = 0 时， d y
τ =τ0
不符合第一个
沙浆， 条件 ，如：沙浆，矿浆等 2 屈服塑张流体：其特征为 屈服塑张流体： dv n τ = τ 0 + µ( ) dy 两个条件均不满足 图1-4 牛顿流体与非牛顿流体 3 似塑性流体： 似塑性流体： d v n τ = (µ ) d y 注意：我们以后所讨论的流体均为牛顿流体。 注意：我们以后所讨论的流体均为牛顿流体。
2011-12-18
21
1.4.3 流体的静压力及其特点： 流体的静压力及其特点：
1 . 流体静压力的作用方向
与作用面垂直， 与作用面垂直，并由外 用面。 向内指向作 用面。 用反证法来证明
假定移去如图所示的一团 流体的上部后作用力F 流体的上部后作用力 的方 向不垂直于作用面A， 向不垂直于作用面 ，则F 可分解为法向力和切向力， 可分解为法向力和切向力， 而由于切向力的存在这团流 体就不会保持平衡而产生流 所以， 必然是法向力 必然是法向力。 动，所以，F必然是法向力。
绝热指数仅与气体的分子 结构有关
2011-12-18
1、3 、
流体的粘性
实验一： 实验一：
穿透水射向平板， 当τ =0时，将一条色线 穿透水射向平板，是一条直线 时 兰色）， ），当 色线变得弯曲起来（ （兰色），当τ ≥ 0时，u水>0色线变得弯曲起来（红线）， 时 色线变得弯曲起来 红线）， 可以看到无论来流的速度是多少，这条色线总是 总是粘附在 可以看到无论来流的速度是多少，这条色线总是粘附在 固体壁面上。 固体壁面上。 这种边界叫无滑移边界（条件） 这种边界叫无滑移边界（条件） 无滑移边界 Vf
2011-12-18
20
1.4
作用在流体上的力
1.4.1 表面力 如法向力（压力），切向力（粘性力） ），切向力 如法向力（压力），切向力（粘性力） 表面力的大小与其表面积的大小呈正比， 表面力的大小与其表面积的大小呈正比，是 作用在表面上的力。 作用在表面上的力。 质量力） 体积力 （质量力） 如重力、惯性力、 如重力、惯性力、电磁力等 质量力的大小与其质量的大小呈正比， 质量力的大小与其质量的大小呈正比，它可 以远距离作用在流体内部的每一个质点上。 以远距离作用在流体内部的每一个质点上。故称 远程力。 远程力。
β=1/273
11
ν2
2011-12-18
=ν1
T 2 T 1
流体的基本性质 当气体的压力不太高（<10kPa) ,或速度不太高 当气体的压力不太高（ 或速度不太高 (<70m/s)时，可认为是不可压缩的。 时 可认为是不可压缩的。 3、绝热时 当气体没有摩擦，又没有热交换时， 、 当气体没有摩擦，又没有热交换时， 可认为是绝热可逆过程 ：
2011-12-18
19
1.3.5 粘性流体与理想流体 实际流体都是具有粘性的，都是粘性流体。 实际流体都是具有粘性的，都是粘性流体。 不具有粘性的流体称为理想流体，这是客观世界上 不具有粘性的流体称为理想流体， 并不存在的一种假想流体。 并不存在的一种假想流体。 （1）在静止流体和速度均匀、直线运动的流体中， ）在静止流体和速度均匀、直线运动的流体中， 流体的粘性表现不出来。 流体的粘性表现不出来。 （2）在许多场合下，想求得粘性流体的精确解是很 ）在许多场合下， 困难的。可以先不计粘性的影响， 困难的。可以先不计粘性的影响，使问题的分析大 为简化，从而有利于掌握流体流动的基本规律。 为简化，从而有利于掌握流体流动的基本规律。至 于粘性的影响则可通过试验加以修正。 于粘性的影响则可通过试验加以修正。
2011-12-18
V Ev = − dp dV
dV <0 dP
10
流体的基本性质 对于气体： 对于气体： 1、 等温时 、 （T1=T2）
P ρ2 = ρ1 2 P 1
P ν2 =ν1 1 P 2
2、 等压时（P1=P2） 、 等压时（
T ρ2 = ρ1 1 T 2
T ρ0 0 = ρt = ρ0 T 1+ βt t
2011-12-18
16
流体的粘性 b.粘性动量通量： 粘性动量通量
通过单位面积在单位时间内传递的动量。 通过单位面积在单位时间内传递的动量。
∂νx µ ∂ρvx ∂ρvx τ = ±µ =± =± υ ∂y ∂y ρ ∂y
υ—运动粘性系数 单位： υ—运动粘性系数，单位：m2/s 运动粘性系数， 粘性动量通量的大小与动量梯度成正比 方向：总是从高速流层传向低速流层。 方向：总是从高速流层传向低速流层。 既粘性动量的传递方向指向速度梯度的负值方向。 既粘性动量的传递方向指向速度梯度的负值方向。使得 计算结果中，粘性动量通量总是大于等于零。 计算结果中，粘性动量通量总是大于等于零。 即：粘性动量通量 ∂vx τ粘 = ±µ ≥0 ∂y