第3章 解题指导(理论力学 金尚年 第二版)
- 格式:ppt
- 大小:470.52 KB
- 文档页数:14
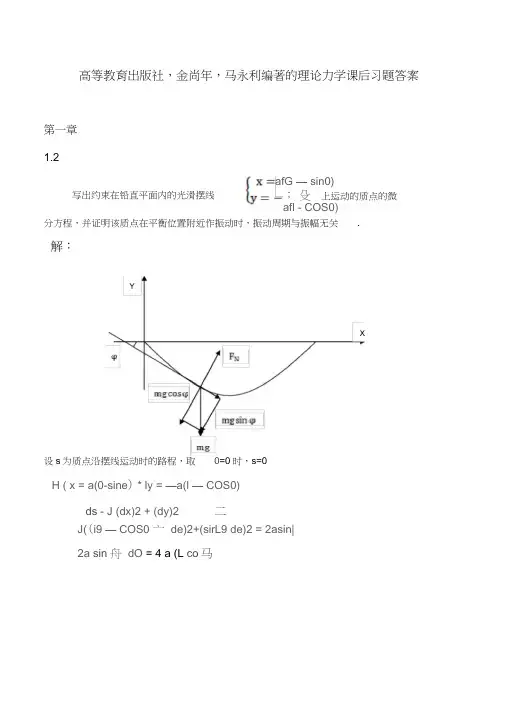
高等教育出版社,金尚年,马永利编著的理论力学课后习题答案第一章1.2afG — sin0);殳上运动的质点的微写出约束在铅直平面内的光滑摆线afl - COS0)分方程,并证明该质点在平衡位置附近作振动时,振动周期与振幅无关.解:设s为质点沿摆线运动时的路程,取0=0时,s=0H ( x = a(0-sine) * ly = —a(l — COS0)ds - J (dx)2 + (dy)2 二J((i9 — COS0 亠de)2+(sirL9 de)2 = 2asin|2a sin舟dO = 4 a (L co 马ee As=2acos^59 + 2asin?9 = acos| 9^ + 2a sin? 9x轴的夹角,取逆时针为正,tan (p即切线斜率设(P为质点所在摆线位置处切线方向与dy cos 0 -1 tan <p =—=———〒dx sin 01聶siin<p = -cosI受力分析得:ms = —mg sin (p = mg cos-0 •・B・r a贝U2a sin二6 + a cos二6' = geos-,此即为质点的运动微分方程。
S = =(S = 4a)-(S 二4a) + —(s = 4a) =4a—周期性变化的函数,周期T=2TT产P e 该质点在平衡位置附近作振动时,振动周期与振幅无关,为2讥启.1.3证明:设一质量为m的小球做任一角度日0的单摆运动运动微分方程为m(2 + 2「日)=F gmrO = mg sin £给式两边同时乘以d9 r日d£=gsind8对上式两边关于6积分得护jgcog + c利用初始条件日=日0时日=0故c = -gcos£0由可解得0 =-{2& • J c 0 s-c 0 8o上式可化为-岸•J cos。
-cosgd日=dt两边同时积分可得 评J ; J co £o 页迅咼.1卑匸萼严进-步化简可得t 辟 J 站n r由于上面算的过程只占整个周期的1/4故由 s in 2/sin ¥=s z 两边分别对6 3微分可得cos % =s 碍C 。


3.4.2 质量为m 的质点在oxy 平面内运动, 质点的运动学方程为j t b i t a rωωsin cos +=, ω,,b a 为正常数,证明作用于质点的合力总是指向原点. 解题思路:本题已知质点的运动学方程,要求的是力,可运用第二章的知识,求 得加速度,,再运用牛顿运动定律求力.指向原点的意思是力的方向与矢径方 向相反.3.4.4 桌面上叠放着两块木块,质量各为m 1, m 2 ,如图所示, m 2 和桌面的摩擦系数为2μ, m 1, m 2 间的静摩擦系数为1μ, 问水平方向用多大的力才能把下面的物体抽出来.解题思路:本题应先作出受力分析图,可先按极限情况情况讨论刚好抽出 所需要的力。
3.4.5 质量为m2,的斜面可在光滑的水平面上滑动,斜面倾角为α,质量为m1的运动员与斜面之间亦无摩擦,求运动员相对于斜面的加速度及其对斜面的压力.解题思路:本题可用非惯系的方法求,如图所示,将坐标取在斜面上,设斜面后退的加速度为a0,则m1除了受重力、斜面的支持力作用外,还受到一惯性力作用(水平向左)运动员相对斜面的加速度为ar,则对于斜面3.4.6 两物体的质量分别为m 和M,物体之间及物体与桌面间的摩擦系数都为u。
求在力F 的作用下两物体的加速度及绳的张力。
绳不可伸长解:对每一物体受力分析,由牛顿第二定律列方程,对m、M 水平方向的方程为可解得3.4.9 跳伞运动员初张伞时的速率为00=v ,设所受阻力的大小与其速率的两次方成正比2v α,求)(t v v =的函数(即任一时刻的速度)解题思路:阻力是一变力,应先受力分析,列出运动微分方程,通过解微分方程求解.设阻力的大小可表示成2v f α-=,取向下为正方向。
由牛顿第二定律得 dtdv m v mg =-2α 分离变量,两边积分⎰⎰=-dt v mg dv 2α⎰⎰=-dt v gmdvg211α令 v gmx α=则 dx gmdv α=则⎰⎰=-dt xdxg m 21α 积分,得⎰⎰⎰+-+=+--+=++-=-11211ln 21)]1ln()1[ln(21)1(2)1(21C x xC x x x dx x dx x dx 211ln 21C t mg xx +=-+α113232+-=C eC e x t mg t m g αα所以, 113232+-=C eC egm v tmg t mg ααα带入初始条件 0,00==v t , 得到 13=C1122+-=tmg t mg eegm v ααα3.4.11 棒球的质量为0.14kg.用棒击棒球的力随时间的变化如图所示.设棒球被击前后速度增量大小为70m/s,求力的最大值.打击时,不计重力.解题思路:本题用动量定理,球所受的冲量等于球动量的增量,已知力函数求冲量等于曲线下的面积3.4.18 太空旅馆, 用32m 长的绳联结质量相同的客舱, 如果旅客感到与地面相同的重力作用, 需要绕中点转动的角速度多大? 解: 圆周运动的向心加速度为 g r a ==2ω 所以, s rad rg /78.02328.9===ω3.5.2 升降机A 内有一装置如图示.悬挂的两物体的质量各为1m 和2m ,且21m m ≠.若不计绳及滑轮质量,不计轴承处摩擦,绳不可伸长,求当升降机以加速度A(方向向下)运动时,两物体的加速度各是多少?绳内的张力是多少?解题思路:方法一,用非惯性力学解题。


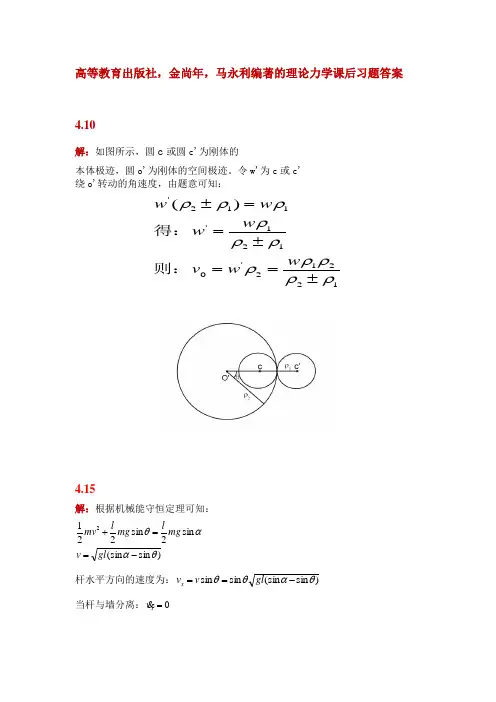
高等教育出版社,金尚年,马永利编著的理论力学课后习题答案 4.10解:如图所示,圆c 或圆c'为刚体的本体极迹,圆o'为刚体的空间极迹。
令w'为c 或c' 绕o'转动的角速度,由题意可知:12212'0121'112')(ρρρρρρρρρρρ±==±==±w w v w w w w 则:得:4.15解:根据机械能守恒定理可知:)sin (sin sin 2sin 2212θααθ-==+gl v mg lmg l mv 杆水平方向的速度为:)sin (sin sin sin θαθθ-==gl v v x当杆与墙分离:0=x v即:0)sin (sin cos )sin (sin cos sin 21=-+--=θαθθαθθgl gl gl v dt d x得:θαsin 23sin = 即:)sin 32arcsin(αθ=4.19如图,该体系中只有一个自由度,取任意位置时棒中点与O 连线与竖直线的夹角θ为广义坐标。
其中设棒的质量为m ,圆周的半径为r ,则棒长为r 3。
另取O 点为重力势能零点。
则对棒θθcos 21212r mg I L o += ,()2221331⎪⎭⎫⎝⎛+=r m r m I o 为棒对O 点的转动惯量。
代入0=∂∂-∂∂θθL L dt d ,得0sin 214522=+θθmgr mr 用θθ=sin 代替,得方程为052=+θθrgrg52=ω,而对于单摆,lg =ω 所以对比得25r l =即等值单摆摆长为25r l =4.20解:如图:设球的半径为R ,设经过时间t 后,会达到如图所示状态,所有参量如图所示。
对其运用牛顿力学方法,有mgRI FR mgma a m F μαμ====''=252mR I =tatv t a v v αω=='=-110同时有对于纯滚动,有 ugtRgt v m m gtv v 25110=='-=ωμμ解上述方程,得代入会得所以有4.23求均匀圆锥体底面圆周上一点的惯量椭球方程。


理论力学(金尚年-XXX编著)课后习题答案详解高等教育出版社的《理论力学课后题答案》一书中,第一章包含了以下三个问题的解答:1.2 题目要求写出在铅直平面内的光滑摆线,并分方程。
解答中使用了微积分和力学原理,得出了运动微分方程。
最后证明了质点在平衡位置附近作振动时,振动周期与振幅无关。
1.3 题目要求证明单摆运动的振动周期与摆长无关。
解答中使用了微积分和力学原理,得出了运动微分方程。
最后通过进一步计算,得出了单摆运动的振动周期公式。
1.5 题目要求使用拉格朗日方程计算质点的运动。
解答中使用了拉格朗日方程,并通过进一步计算得出了质点的运动轨迹。
如图,在半径为R时,地球表面的重力加速度可以由万有引力公式求得:g=\frac{GM}{R^2}$$其中M为地球的质量。
根据广义相对论,地球表面的重力加速度还可以表示为:g=\frac{GM}{R^2}\left(1-\frac{2GM}{c^2R}\right)$$其中c为光速。
当半径增加到R+ΔR时,总质量仍为M,根据XXX展开,可以得到:frac{1}{(R+\Delta R)^2}=\frac{1}{R^2}-\frac{2\DeltaR}{R^3}+\mathcal{O}(\Delta R^2)$$代入上式可得:g'=\frac{GM}{R^2}\left(1-\frac{2GM}{c^2R}\right)\left(1+\frac{2\Delta R}{R}\right)$$ 化简后得:g'=g-\frac{2g\Delta R}{R}$$因此,当半径改变时,表面的重力加速度的变化为:Delta g=-\frac{2g\Delta R}{R}$$2.在平面极坐标系下,设质点的加速度的切向分量和法向分量都是常数,即$a_t=k_1$,$a_n=k_2$(其中$k_1$和$k_2$为常数)。
根据牛顿第二定律,可以得到质点的运动方程:r\ddot{\theta}+2\dot{r}\dot{\theta}=k_2$$ddot{r}-r\dot{\theta}^2=k_1$$其中$r$为极径,$\theta$为极角。


理论力学教案课程名称理论力学任课教师曾奇军所在系(院)物理电子工程学院任课班级物理学本科信阳师范学院《理论力学》课程基本信息(一)课程名称:理论力学(二)学时学分:每周4学时,学分4(三)予修课程:力学、高等数学(四)使用教材:金尚年、马永力编著《理论力学》,第二版.,北京:高等教育出版社,2002年7月,面向21世纪课程教材。
(五)教学参考书:1.周衍柏《理论力学教程》(第二版),北京:高等教育出版社,1986年。
2.郭士望《理论力学》上、下册,北京:高等教育出版社,1982。
3.梁昆森《力学》上、下册,北京:人民教育出版社,1979。
(六)教学方法:课堂讲授,启发式教学(七)教学手段:传统讲授与多媒体教学相结合(八)考核方式:闭卷考试占总成绩70%,平时作业成绩占30%(九)学生创新精神与实践能力的培养方法:在课程讲授过程中注意采用启发式教学手段,将基本的概念和规律讲清、讲透,而将一些具有推广性的问题留给学生思考,以此来提高学生分析问题、解决问题的能力。
并且在课堂讲授时多联系实际的力学问题,以此来提高学生解决实际问题的能力。
(十)其他要求:每堂课后布置适量的课后作业并定期批改、检查和给出成绩,这部分成绩将占期末总成绩的30%。
绪论一:《理论力学》课程的内容:该课程是以牛顿力学和分析力学为主要内容的力学理论,是理论物理的第一门课程。
是从物理学的基本经验规律出发,借助于微积分等数学工具,推导出关于物体机械运动时所满足的整体规律的一门课程。
二:《理论力学》与《力学》的区别和联系1.内容:《理论力学》包括牛顿力学和分析力学,是《力学》课程的深入和提高;而《力学》课程仅讲授牛顿力学,且研究的深度不及《理论力学》。
2.研究手段:《力学》是从物理现象出发,通过归纳总结出物质运动的规律。
《理论力学》是从经验规律出发,借助于数学工具,推导出物质运动所满足的规律,并通过实践来检验该规律的真伪,着重培养学生理性思维的能力。
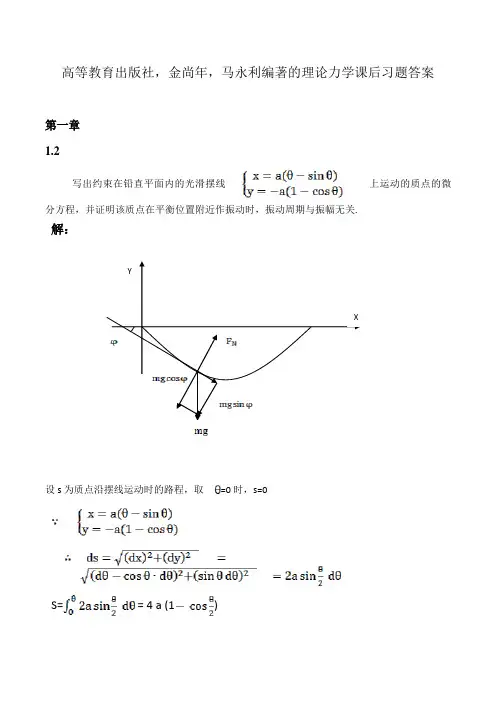
高等教育出版社,金尚年,马永利编著的理论力学课后习题答案第一章1.2写出约束在铅直平面内的光滑摆线上运动的质点的微分方程,并证明该质点在平衡位置附近作振动时,振动周期与振幅无关.解:设s为质点沿摆线运动时的路程,取=0时,s=0 S== 4 a (1) XY设为质点所在摆线位置处切线方向与x 轴的夹角,取逆时针为正,即切线斜率=受力分析得:则,此即为质点的运动微分方程。
该质点在平衡位置附近作振动时,振动周期与振幅无关,为.1.3证明:设一质量为m 的小球做任一角度0θ的单摆运动运动微分方程为θθθF r r m =+)2( θθsin mg mr = ①给①式两边同时乘以d θ θθθθd g d r sin = 对上式两边关于θ积分得 c g r +=θθcos 212 ② 利用初始条件0θθ=时0=θ 故0cos θg c -= ③ 由②③可解得 0cos cos 2-θθθ-•=lg 上式可化为dt d lg=⨯-•θθθ0cos cos 2-两边同时积分可得θθθθθθθθd g l d g l t ⎰⎰---=--=020222002sin 12sin 10012cos cos 12进一步化简可得θθθθd g l t ⎰-=0002222sin sin 121 由于上面算的过程只占整个周期的1/4故⎰-==0222sin 2sin 124T θθθθd g l t由ϕθθsin 2sin /2sin 0=两边分别对θϕ微分可得ϕϕθθθd d cos 2sin 2cos 0=ϕθθ202sin 2sin 12cos-=故ϕϕθϕθθd d 202sin 2sin 1cos 2sin2-= 由于00θθ≤≤故对应的20πϕ≤≤故ϕϕθϕθϕθθθθπθd g l d g l T ⎰⎰-=-=202022cos 2sinsin 2sin 1/cos 2sin42sin2sin 2故⎰-=2022sin 14πϕϕK d g l T 其中2sin022θ=K 通过进一步计算可得glπ2T =])2642)12(531()4231()21(1[224222 +⨯⨯⨯⨯-⨯⨯⨯⨯++⨯⨯++n K n n K K1.5zp点yx解:如图,在半径是R的时候,由万有引力公式,对表面的一点的万有引力为, ①M为地球的质量;可知,地球表面的重力加速度g , x为取地心到无限远的广义坐标,,②联立①,②可得:,M为地球的质量;③当半径增加,R2=R+,此时总质量不变,仍为M,此时表面的重力加速度可求:④Be ө e tөy由④得:⑤则,半径变化后的g 的变化为⑥对⑥式进行通分、整理后得:⑦对⑦式整理,略去二阶量,同时远小于R ,得⑧则当半径改变 时,表面的重力加速度的变化为:。
力学(第二版)漆安慎习题解答第三章动量定理及其守恒定律第三章 动量定理及其守恒定律一、基本知识小结1、牛顿运动定律适用于惯性系、质点,牛顿第二定律是核心。
矢量式:22dtr d m dt v d m a m F === 分量式:(弧坐标)(直角坐标)ρτττ2,,,v m ma F dt dv m ma F ma F ma F ma F n n z z y y x x =======2、动量定理适用于惯性系、质点、质点系。
导数形式:dtp d F =;微分形式:p d dt F=;积分形式:p dt F I∆==⎰)((注意分量式的运用)3、动量守恒定律适用于惯性系、质点、质点系。
若作用于质点或质点系的外力的矢量和始终为零,则质点或质点系的动量保持不变。
即∑==恒矢量。
则,若外p F0(注意分量式的运用)4、在非惯性系中,考虑相应的惯性力,也可应用以上规律解题。
在直线加速参考系中:0*a m f-=在转动参考系中:ωω⨯=='2,*2*mv f r m f k c5、质心和质心运动定理⑴∑∑∑===i i c i i c i i c a m a m v m v m r m r m⑵∑=c a m F(注意分量式的运用)二、思考题解答3.1试表述质量的操作型定义。
解答,kgv v m m 00 ∆∆= 式中kg 1m 0=(标准物体质量);0v∆:为m 与m 0碰撞m 0的速度改变;v∆:为m 与m 0碰撞m 的速度改变,这样定义的质量,其大小反映了质点在相互作用的过程中速度改变的难易程度,或者说,其量值反映了质量惯性的大小。
这样定义的质量为操作型定义。
3.2如何从动量守恒得出牛顿第二、第三定律,何种情况下牛顿第三定律不成立? 解答,由动量守恒 )p p (p p ,p p p p 22112121-'-=-'+='+' ,p p 21∆-=∆t p t p 21∆∆-=∆∆,取极限dt p d dt p d 21 -=动量瞬时变化率是两质点间的相互作用力。
高等教育出版社,金尚年,马永利编著的理论力学课后习题答案第一章1.2写出约束在铅直平面内的光滑摆线上运动的质点的微分方程,并证明该质点在平衡位置附近作振动时,振动周期与振幅无关. 解:设s为质点沿摆线运动时的路程,取=0时,s=0S== 4 a (1)设为质点所在摆线位置处切线方向与x 轴的夹角,取逆时针为正,即切线斜率=受力分析得:则,此即为质点的运动微分方程。
该质点在平衡位置附近作振动时,振动周期与振幅无关,为.1.3证明:设一质量为m 的小球做任一角度0θ的单摆运动运动微分方程为θθθF r r m =+)2( θθsin mg mr = ①给①式两边同时乘以d θ θθθθd g d r s i n = 对上式两边关于θ 积分得 c g r +=θθc o s 212 ②利用初始条件0θθ=时0=θ 故0cos θg c -= ③ 由②③可解得 0c o s c o s 2-θθθ-∙=lg 上式可化为dt d lg=⨯-∙θθθ0cos cos 2-两边同时积分可得θθθθθθθθd g l d g l t ⎰⎰---=--=020222002sin 12sin 10012cos cos 12进一步化简可得θθθθd g l t ⎰-=0002222sin sin 121 由于上面算的过程只占整个周期的1/4故⎰-==0222sin 2sin 124T θθθθd g l t由ϕθθsin 2sin /2sin 0=两边分别对θϕ微分可得ϕϕθθθd d cos 2sin 2cos 0=ϕθθ202sin 2sin 12cos-=故ϕϕθϕθθd d 202sin 2sin 1cos 2sin2-= 由于00θθ≤≤故对应的20πϕ≤≤故ϕϕθϕθϕθθθθπθd g l d g l T ⎰⎰-=-=202022cos 2sinsin 2sin 1/cos 2sin42sin2sin 2故⎰-=2022sin 14πϕϕK d g l T 其中2sin022θ=K 通过进一步计算可得glπ2T =])2642)12(531()4231()21(1[224222 +⨯⨯⨯⨯-⨯⨯⨯⨯++⨯⨯++n K n n K K1.5解:如图,在半径是R 的时候,由万有引力公式, 对表面的一点的万有引力为, ①M 为地球的质量;可知,地球表面的重力加速度 g , x 为取地心到无限远的广义坐标,,②联立①, ②可得:,M 为地球的质量;③当半径增加 ,R2=R+ ,此时总质量不变,仍为M,此时表面的重力加速度 可求:④由④得:⑤则,半径变化后的g 的变化为⑥对⑥式进行通分、整理后得:⑦对⑦式整理,略去二阶量,同时远小于R ,得⑧则当半径改变 时,表面的重力加速度的变化为:。
第零章 数学准备一 泰勒展开式1 二项式的展开()()()()()m 23m m-1m m-1m-2f x 1x 1mx+x x 23=+=+++!!2 一般函数的展开()()()()()()()()230000000f x f x f xf x f x x-x x-x x-x 123!''''''=++++!!特别:00x =时,()()()()()23f 0f 0f 0f x f 0123!x x x ''''''=++++!!3 二元函数的展开(x=y=0处)()()00f f f x y f 0x+y x y ⎛⎫∂∂=++ ⎪∂∂⎝⎭,22222000221f f f x 2xy+y 2x x y y ⎛⎫∂∂∂++ ⎪ ⎪∂∂∂∂⎝⎭!评注:以上方法多用于近似处理与平衡态处的非线性问题向线性问题的转化。
在理论力问题的简单处理中,一般只需近似到三阶以内。
二 常微分方程1 一阶非齐次常微分方程: ()()x x y+P y=Q通解:()()()P x dx P x dx y e c Q x e dx -⎛⎫⎰⎰=+ ⎪⎝⎭⎰注:()()(),P x dx P x dx Q x e dx ⎰±⎰⎰积分时不带任意常数,()x Q 可为常数。
2 一个特殊二阶微分方程2y A y B =-+ 通解:()02B y=K cos Ax+Aθ+注:0,K θ为由初始条件决定的常量 3 二阶非齐次常微分方程 ()x y ay by f ++=通解:*y y y =+;y 为对应齐次方程的特解,*y 为非齐次方程的一个特解。
非齐次方程的一个特解 (1) 对应齐次方程0y ay by ++=设x y e λ=得特征方程2a b 0λλ++=。
解出特解为1λ,2λ。
*若12R λλ≠∈则1x 1y e λ=,2x 2y e λ=;12x x 12y c e c e λλ=+*若12R λλ=∈则1x 1y e λ=,1x 2y xe λ=; 1x 12y e (c xc )λ=+*若12i λαβ=±则x 1y e cos x αβ=,x 2y e sin x αβ=;x 12y e (c cos x c sin x)αββ=+(2) 若()2000x f a x b x c =++为二次多项式*b 0≠时,可设*2y Ax Bx C =++ *b 0≠时,可设*32y Ax Bx Cx D =+++注:以上1c ,2c ,A,B,C,D 均为常数,由初始条件决定。
高等教育出版社,金尚年,马永利编著理论力学课后习题答案第一章1.2写出约束在铅直平面内的光滑摆线上运动的质点的微分方程,并证明该质点在平衡位置附近作振动时,振动周期与振幅无关.解:设s为质点沿摆线运动时的路程,取=0时,s=0XYF Nmg sinφmgmg cosφφS== 4 a (1)设为质点所在摆线位置处切线方向与x 轴的夹角,取逆时针为正,即切线斜率=受力分析得:则,此即为质点的运动微分方程。
该质点在平衡位置附近作振动时,振动周期与振幅无关,为.1.3证明:设一质量为m 的小球做任一角度0θ的单摆运动运动微分方程为θθθF r r m =+)2( θθsin mg mr = ①给①式两边同时乘以d θ θθθθd g d r sin = 对上式两边关于θ积分得 c g r +=θθcos 212 ② 利用初始条件0θθ=时0=θ 故0cos θg c -= ③ 由②③可解得 0cos cos 2-θθθ-•=lg 上式可化为dt d lg=⨯-•θθθ0cos cos 2-两边同时积分可得θθθθθθθθd g l d g l t ⎰⎰---=--=020222002sin 12sin 10012cos cos 12进一步化简可得θθθθd g l t ⎰-=0002222sin sin 121 由于上面算的过程只占整个周期的1/4故⎰-==0222sin 2sin 124T θθθθd g l t由ϕθθsin 2sin /2sin 0=两边分别对θϕ微分可得ϕϕθθθd d cos 2sin 2cos 0=ϕθθ202sin 2sin 12cos-=故ϕϕθϕθθd d 202sin 2sin 1cos 2sin2-= 由于00θθ≤≤故对应的20πϕ≤≤故ϕϕθϕθϕθθθθπθd g l d g l T ⎰⎰-=-=202022cos 2sinsin 2sin 1/cos 2sin42sin2sin 2故⎰-=2022sin 14πϕϕK d g l T 其中2sin022θ=K 通过进一步计算可得glπ2T =])2642)12(531()4231()21(1[224222 +⨯⨯⨯⨯-⨯⨯⨯⨯++⨯⨯++n K n n K K1.5zp点yx解:如图,在半径是R的时候,由万有引力公式,对表面的一点的万有引力为, ①M为地球的质量;可知,地球表面的重力加速度 g , x为取地心到无限远的广义坐标,,②联立①,②可得:,M为地球的质量;③当半径增加 ,R2=R+ ,此时总质量不变,仍为M,此时表面的重力加速度可求:④e өe tөy由④得:⑤则,半径变化后的g 的变化为⑥对⑥式进行通分、整理后得:⑦对⑦式整理,略去二阶量,同时远小于R ,得⑧则当半径改变 时,表面的重力加速度的变化为:。