PM2.5 浓度地理加权回归计算方法

卫星遥感细颗粒物（PM2.5）监测技术指南1 适用范围本标准规定了卫星遥感细颗粒物监测的方法、结果验证、质量控制等内容。

本标准适用于陆地区域卫星遥感细颗粒物监测工作，作为地面监测手段的补充，用于掌握大范围细颗粒物空间分布规律及变化趋势。

2 规范性引用文件本标准引用了下列文件或其中的条款。

凡是注明日期的引用文件，仅注日期的版本适用于本标准。

凡是未注日期的引用文件，其最新版本（包括所有的修改单）适用于本标准。

HJ 93 环境空气颗粒物（PM10和PM2.5）采样器技术要求及检测方法HJ 653 环境空气颗粒物（PM10和PM2.5）连续自动监测系统技术要求及检测方法HJ 655 环境空气颗粒物（PM10和PM2.5）连续自动监测系统安装和验收技术规范HJ 817 环境空气颗粒物（PM10和PM2.5）连续自动监测系统运行和质控技术规范3 术语和定义下列术语和定义适用于本标准。

3.1气溶胶光学厚度 aerosol optical depth（AOD）从地面到大气层顶垂直路径中整层气溶胶消光系数的总和，量纲为1。

3.2像元PM2.5浓度 pixel PM2.5 concentration卫星观测1个像元范围内的近地面大气细颗粒物平均质量浓度，计量单位为μg /m3。

3.3行星边界层高度 planetary boundary layer height（PBLH）行星边界层也称摩擦层或大气边界层，是对流层的最下层，一般自地面到1 km～2 km高度；行星边界层高度是指从地面到行星边界层顶的高度，表示污染物在垂直方向能被热力湍流所扩散的范围。

3.4地理加权回归 geographically weighted regression（GWR）一种用回归原理研究具有空间（或区域）分布特征的两个或多个变量之间数量关系的方法，在数据处理时考虑局部特征作为权重。

4 总则4.1 监测原理根据PM2.5质量浓度与AOD、吸湿增长因子、密度、半径、消光效率因子及行星边界层高度等因素的转化关系计算PM2.5质量浓度。

太原市PM2.5浓度的气象特征影响分析及预报太原市PM2.5浓度的气象特征影响分析及预报一、引言PM2.5（细颗粒物）是空气中直径小于或等于2.5微米的颗粒物，是空气质量中一项重要的指标。

它对空气质量和人体健康具有重要影响。

太原市作为山西省的省会城市，工业发展较快，产生大量的污染物，PM2.5浓度较高。

了解太原市PM2.5的气象特征以及其影响因素，对于改善空气质量，保护人民健康意义重大。

二、太原市PM2.5的气象特征1. 季节变化特征太原市PM2.5浓度的季节变化特征明显，冬季浓度较高，春季次之，夏季最低。

冬季PM2.5浓度高主要是由于冬季气温较低，空气稳定，大气层中污染物无法扩散。

此外，冬季太原市采暖季节，大量使用燃煤取暖，释放的污染物直接导致PM2.5浓度的增加。

2. 时间变化特征太原市PM2.5的时间变化特征显示出明显的日间和夜间差异。

白天期间，太阳辐射增强，温度升高，大气不稳定，污染物较容易扩散，导致PM2.5浓度较低。

而夜间，太阳辐射减弱，温度降低，大气稳定，污染物扩散受限，PM2.5浓度呈现明显上升趋势。

3. 地理位置特征太原市地处山西盆地，地势低洼，环境风能力较差。

尤其当气象条件不利于污染物扩散时，PM2.5浓度会进一步上升。

加之周边地区工业污染物排放较多，风向不利时，太原市PM2.5浓度会受到周边地区影响而增加。

三、太原市PM2.5浓度的影响因素分析1. 温度温度是影响太原市PM2.5浓度的重要因素之一。

冬季温度较低，大气稳定，污染物扩散受限，导致PM2.5浓度上升。

夏季温度较高，大气不稳定，污染物扩散较快，PM2.5浓度相对较低。

2. 风速和风向风速和风向是影响太原市PM2.5浓度的另外两个关键因素。

风速较低时，污染物扩散受限，PM2.5浓度较高。

风向直接影响了来自周边地区的工业污染物对太原市PM2.5浓度的影响方向。

3. 气压和湿度气压和湿度也对PM2.5浓度有一定影响。

气压较低时，大气稳定，污染物扩散受限，PM2.5浓度较高。

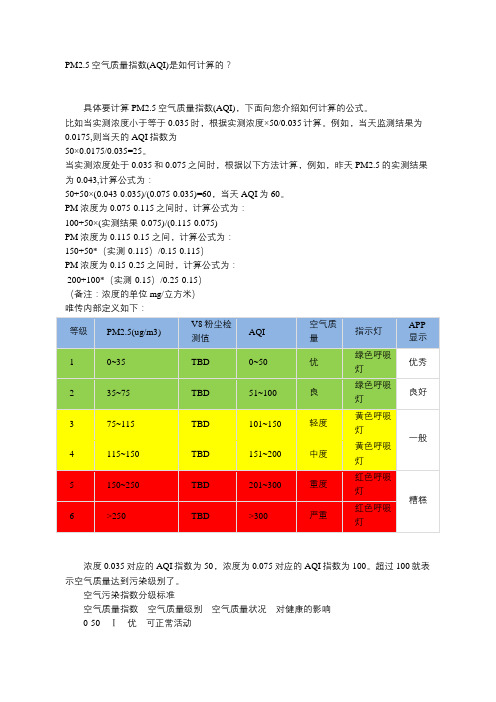
PM2.5空气质量指数(AQI)是如何计算的？具体要计算PM2.5空气质量指数(AQI)，下面向您介绍如何计算的公式。

比如当实测浓度小于等于0.035时，根据实测浓度×50/0.035计算。

例如，当天监测结果为0.0175,则当天的AQI指数为50×0.0175/0.035=25。

当实测浓度处于0.035和0.075之间时，根据以下方法计算，例如，昨天PM2.5的实测结果为0.043,计算公式为：50+50×(0.043-0.035)/(0.075-0.035)=60，当天AQI为60。

PM浓度为0.075-0.115之间时，计算公式为：100+50×(实测结果-0.075)/(0.115-0.075)PM浓度为0.115-0.15 之间，计算公式为：150+50*（实测-0.115）/0.15-0.115）PM浓度为0.15-0.25之间时，计算公式为：200+100*（实测-0.15）/0.25-0.15）（备注：浓度的单位mg/立方米）唯传内部定义如下：浓度0.035对应的AQI指数为50，浓度为0.075对应的AQI指数为100。

超过100就表示空气质量达到污染级别了。

空气污染指数分级标准空气质量指数空气质量级别空气质量状况对健康的影响0-50Ⅰ优可正常活动51-100Ⅱ良可正常活动101-150Ⅲ1轻微污染长期接触，易感人群出现症状151-200Ⅲ2轻度污染长期接触，健康人群出现症状201-250Ⅳ1中度污染一定时间接触后，健康人群出现症状251-300Ⅳ2中度重污染一定时间接触后，心脏病和肺病患者症状显著加剧>300Ⅴ重度污染健康人群明显强烈症状，提前出现某些疾病。

第30卷第10期干旱区资源与环境Vol．30No．10 2016年10月Journal of Arid LandＲesources and Environment Oct．2016文章编号：1003－7578（2016）10－116－05doi：10．13448/j．cnki．jalre．2016．327土地利用回归模型模拟京津冀PM2．5浓度空间分布*许刚1，焦利民1，2，肖丰涛1，赵素丽1，张欣1（1．武汉大学资源与环境科学学院，武汉430079；2．武汉大学地理信息系统教育部重点实验室，武汉430079）提要：PM2．5污染暴露评估需要浓度空间分布数据，而稀疏的地面监测点无法满足要求。

土地利用回归（LUＲ）模型是模拟大气污染物浓度的有效方法，本研究拟探讨LUＲ模型在中国区域尺度的适用性及精度。

选取土地利用、道路交通、人口密度、工业污染源、高程、气象共6类变量建立区域LUＲ模型模拟京津冀地区2013年PM2．5浓度空间分布。

以研究区80个监测点为中心建立0．1km 10km共22个系列缓冲区，表征不同尺度下各变量对PM2．5浓度的影响。

双变量相关分析得出161个影响因子与PM2．5浓度的相关性水平，筛选出13个影响因子与PM2．5浓度进行逐步多元线性回归，得到区域LUＲ模型。

交叉验证显示模型拟合精度（Ｒ2）达到78．7%，模拟结果显示京津冀PM2．5污染南北差异明显。

关键词：土地利用回归；PM2．5；空间分布；京津冀中图分类号：X531文献标识码：APM2．5指空气动力学当量直径小于等于2．5μm的颗粒物，也称细颗粒物，由于其易吸入性且易粘带有毒物质，严重危害人体健康；而PM2．5污染暴露评估需要连续一致的浓度空间分布数据，但稀疏的地面监测点无法满足要求。

地理信息科学技术的发展为大气污染物浓度模拟提供了新的技术手段，如空间插值模型、土地利用回归模型、遥感方法等［1］。

Briggs等（1997）利用多元线性回归模拟了欧洲阿姆斯特丹等城市NO2浓度空间分布，并将该方法称为回归制图（Ｒegression Mapping）［2］。

附录A （资料性附录）PM 2.5浓度地理加权回归计算方法根据监测原理形成PM 2.5浓度矩阵计算公式如下：Y X b = （A.1）其中，因变量矩阵Y 、自变量矩阵X 和回归系数矩阵β根据匹配后的数据构建，构建形式如下：2.5112.5222.5ln(((,)))ln(((,)))ln(((,))n n M PM u v M PM u v Y M PM u v éùêúêú=êúêúëûM （A.2） 111111222222ln((,))ln((,))ln(1(,)/100)ln((,))ln((,))ln(1(,)/100)ln((,))ln((,))ln(1(,)/100)n n n n n n AOD u v HPBL u v RH u v AOD u v HPBL u v RH u v X AOD u v HPBL u v RH u v -éùêú-êú=êúêú-ëûM M M （A.3） 0110220111122121122223113333(,)(,)(,)(,)(,)(,)(,)(,)(,)(,)(,)(,)n n n n n n n n u v u v u v u v u v u v u v u v u v u v u v u v b b b b b b b b b b b b b éùêúêú=êúêúëûLL L L（A.4） 公式（A.2）、（A.3）和（A.4）中：2.5ln(((,)))i i M PM u v ——第i 个训练样本的PM 2.5浓度自然对数； ln((,))i i AOD u v ——第i 个训练样本的气溶胶光学厚度自然对数； ln((,))i i HPBL u v ——第i 个训练样本的边界层高度自然对数；ln(1(,)/100)i i RH u v -——第i 个训练样本的相对湿度线性变化后的自然对数； 0(,)i i u v b 、1(,)i i u v b 、2(,)i i u v b 、3(,)i i u v b ——第i 个训练样本的回归系数；i u ——第i 个训练样本的地理横坐标； i v ——第i 个训练样本的地理纵坐标。

黑龙江省PM2.5浓度与土地利用的相关性分析田若颖，周嘉*，徐畅（哈尔滨师范大学地理科学学院，黑龙江哈尔滨150500）摘要:基于2010－2020年黑龙江省PM2.5浓度数据及土地利用/覆被变化（LUCC）数据，对该省PM2.5及LUCC进行了时空分布特征分析，并利用Arc GIS空间分析、地理加权回归等手段探讨PM2.5变化与LUCC的相关性。

结果表明，①黑龙江省11年来PM2.5年均浓度的空间格局均为西南高、东北低。

时间格局呈先上升、后下降的趋势；②2010－2020年黑龙江省土地利用类型/覆被以耕地、林地为主。

土地利用类型面积变化主要为林地、草地转为人造地表；③通过GWR进行响应分析发现，PM2.5变化对土地利用/覆被变化有显著的响应作用。

当林地草地转化为人造地表时PM2.5浓度上升，而耕地及人造地表转为林地草地时PM2.5浓度降低。

因此，增加绿地面积对于防止PM2.5浓度上升具有重要作用。

关键词:PM2.5；土地利用/覆被变化（LUCC）；地理加权回归（GWR）；空间响应PM2.5作为大气中的细小颗粒，具有极高的悬浮性和潜在的健康风险。

目前，PM2.5的研究已经成为全球环境科学领域的热点之一。

研究人员通过监测和模拟等手段，探究PM2.5的来源、传输、化学成分、健康影响等问题[1-2]。

PM2.5的时空分布受到众多因素的影响，但对其与土地覆被变化的关系研究较少。

随着近年来城市化的快速发展，我国土地利用/覆被变化（LUCC）发生了巨大变化，下垫面类型的变化对PM2.5浓度的时空分布产生了影响。

因此，分析LUCC与PM2.5浓度相关性，能以有效缓解PM2.5污染的角度对国土规划布局提供建议和思路。

目前，关于土地利用和PM2.5的研究主要集中在以下方面：（1）研究土地利用类型和PM2.5浓度的时空相关性，大部分研究以单个城市为单位，分析该研究区域内LUCC与PM2.5浓度的相关性[3-4]；（2）构建土地利用回归模型（LUR）探究对PM2.5浓度的影响，以期预测该研究区内PM2.5的未来变化趋势；还有部分研究分析城市景观格局对PM2.5浓度的影响，研究者利用景观格局分析法和空间统计方法，发现不同景观类型和景观格局指数与PM2.5浓度之间存在密切关系。

基于MAIAC AOD反演和两阶段模型的美国东南部地面PM2.5浓度估计摘要：以往的研究表明，细颗粒物（PM2.5，空气动力学直径小于2.5微米的颗粒）与多种健康问题有关。

实地测量是PM2.5浓度测量的最好标准，但耗时且昂贵。

利用遥感图像反演的气溶胶光学厚度（AOD）产品可以辅助地面监测网络进行PM2.5在时间与空间上的估计。

然而，在以往的研究中使用的粗分辨率（如10公里）的AOD产品很难估计城市规模的PM2.5浓度，准确的预测PM2.5的浓度对研究PM2.5对健康的影响是至关重要的。

在本文中，我们使用带有气象场（例如，风速）和土地使用参数（例如，森林覆盖，道路长度，高程和点的排放量）作为辅助变量的两阶段空间统计模型算法对由多角度大气校正（MAIAC）算法派生出来的一种新产品进行检测，从而估计每天的PM2.5浓度。

本文的研究区位于美国东南部，研究中使用的2003年的数据由多种渠道收集。

模型采用交叉验证的方法。

我们得到的R 2为0.83，模型拟合的平均预测误差（MPE）为1.89微克/立方米，预测均方差的平方根误差（RMSPE）为2.73微克/立方米，交叉验证的R 2为0.67，MPE为2.54微克/立方米，RMSPE为3.88微克/立方米。

模型拟合和交叉验证均表明因变量和预测变量之间拟合良好。

研究结果表明，空间分辨率为1公里的MAIAC AOD可用于估计PM2.5浓度。

关键词：气溶胶光学厚度； MAIAC ；MODIS ；PM2.5；两阶段模型1 引言许多流行病学研究表明，PM2.5（空气动力学直径小于2.5微米的颗粒）与包括心血管和呼吸系统疾病在内的多种健康问题有关（Dominici等人，2006;Gauderman等人，2004;Gold 等人，2000; Peters, Dockery, Muller与Mittleman，2001;Schwartz与 Neas，2000）。

可通过计算住在离中心一定距离内的人口（例如几公里（Laden, Schwartz，Speizer，Dockery，2006）到几十公里（Samet，Dominici，Curriero，Coursac与Zeger， 2000））来估计受到PM2.5影响的人数。