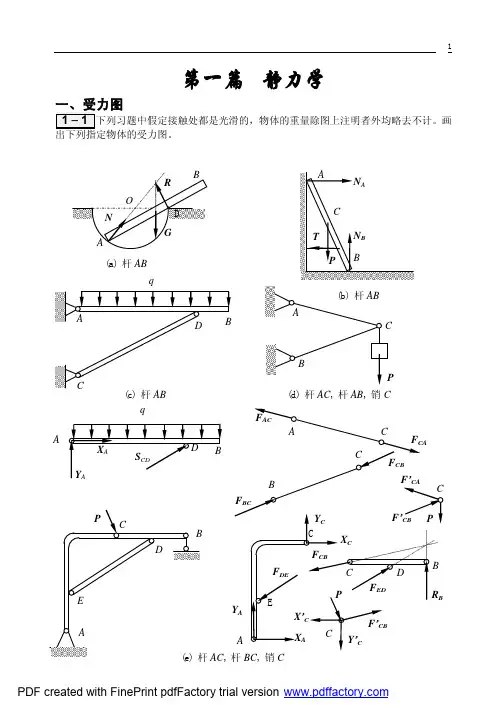
用摩擦角巧解静力学问题
- 格式:doc
- 大小:22.00 KB
- 文档页数:3

用全反力及摩擦角巧解力学问题力学问题中常涉及的平面与斜面上运动的模型,是高考经常考查的内容。
在求解力的过程中常涉及力的极值计算,常规的方法为将力正交分解,列方程组计算或讨论。
计算过程中有关三角函数的计算较为繁琐,若用全反力解题会是问题简洁明了。
我们知道,物体之间的滑动摩擦力与弹力总是垂直且成正比,如图1所示。
将支持力F N 与滑动摩擦力f 的合力叫做全反力,则全反力F 全与支持力F N 之间的夹角α=arctan NF f=arctan μ可知,夹角α是一个定值,这个角叫摩擦角。
摩擦角只决定于动摩擦因数,即全反力的大小可变,但方向不变。
一、用全反力巧解匀速直线运动状态的问题(1)平面类例:如图2所示,一物块置于水平地面上。
当用于水平方向成60°角的力F 1拉物块时,物块做匀变速直线运动;当改用与水平方向成30°角的力F 2推物块时,物块仍做匀速直线运动。
若F 1和F 2的大小相等,则物块与地面之间的动摩擦因数为( )A. 1-3B.32-C.2123-D.231-解析:两次作用力下物体都向右做匀速直线运动,两次全反力大小不同但方向相同,受力情况如图3所示,现将两次全反力F 全,重力mg 及拉力F 矢量平移可得到如图4所示的矢量图。
因∠2+∠3=60°,有∠1=30°,又因∠4=30°,则∠4+∠2+∠3=90°由题意知F 1,F 2相等,则F 1,F 2关于垂线段对称。
则∠2=45°;所以全反角α=15°。
既有αμtan =又tan15°=︒+︒30cos 130sin 可解得3-2=μ(2)斜面类例:如图5所示,将质量为m 的滑块放在倾角为θ的固体斜面上。
滑块与斜面之间的动摩擦因数为μ。
若滑块与斜面之间的最大静摩擦力与滑动摩擦力大小相等,重力加速度为g ,则A. 将滑块由静止释放,如果θμtan >,滑块将下滑B. 给滑块沿斜面向下的初速度,如果θμtan <,滑块将减速下滑C. 用平行于斜面向上的力拉滑块向上匀速滑动,如果θμtan =,拉力大小应是2mgsin θD. 用平行于斜面向下的力拉滑块向下匀速滑动,如果θμtan =,拉力大小应为mgsin θ解析:若拉力沿斜面向上,对物体受力分析如图6(a )所示,滑块沿斜面向上匀速滑动,且θμtan =,则有摩擦角θα=,平移全反力F 全,重力mg 及拉力F 可构成首尾相接的闭合矢量三角形,如图6(b )所示,显然F=2mgsin θ,选项C 正确。

来源于网络图4物体的平衡之巧妙方法——摩擦角的应用一、 摩擦角的定义摩擦角指的是:物体在受到摩擦力情况下,物体的滑动摩擦力(或最大静摩擦力)f N F F μ=,支持面的支持力N F 的方向固定不变,我们将支持力与摩擦力合成为支持面作用力F (以下讲到的斜面对物体的作用力或平面对物体的作用力都为此力),则支持面的作用力F 与支持力N F 的方向成1tan μ-角(如图1所示),而这个角就称之为摩擦角。
解析:由摩擦公式: f N F F μ= 得tan fF μϕ==,解析:由μ=得,摩擦角110tan tan303ϕμ--===,作出力的三角形,如图5所示,蓝色有向线段为重力,黑色射线为斜面对物块的作用力,红色有向线段为施加的力,青色有向线段为施加的力的最小位置(与斜面的作用力相垂直),则00sin(45)sin15F mg mgϕ=-=方向与水平成15o斜向右。
即A正确。
例3,(2009.辽宁、宁夏理综)水平地面上有一木箱,木箱与地面之间的动摩擦因数为(01)μμ<<。
现对木箱施加一拉力F,使木箱做从0逐渐sinFθ,F=F先减小P=F,蓝90°的过F先减小后增大。
对于F1F F G+=-,重力的功率显然为90o),功率11cosP F vψ=∙,显然F1不结论:对比两种方法,方法二显然要简单容易的多。
因此高中有必要掌握摩擦角的应用,而不一定非得参加竞赛的学生才掌握。
例4,(竞赛训练题)如图8所示,质量为m的物体放在水平地面上,物体与地面的动摩擦因素3μ=,想用力F推动物体沿水平地面滑动,推力方向与水平夹角在什么范围内事可能的?答案:0160sin2mgFθ-≤-图9来源于网络 解析:摩擦角10tan 30ψμ-==,考虑临界情况,重力mg 、地面对物体的作用力以及推力F 构成闭合三角形时,则有00sin(60)sin mg F θϕ=-,临界角01060sin 2mg F θ-=-,由图9可知0θθ≤时物体可在地面上滑动。


自主招生物理静力学拓展知识定位静力学作为高中物理的重要基础,在自主招生的考试中也是常客,除了基础的物体的平衡以及受力分析技巧的考察外,摩擦角等技巧也是经常出现在自主招生考试中。
总体而言,静力学考点在自主招生考试中的难度(除了华约的计算题,以及早年清华大学外)相对比较容易。
知识梳理➢知识点一:摩擦角➢ 知识点二:一般物体的平衡条件例题精讲【试题来源】2011年卓越自主招生【题目】1、明理同学平时注意锻炼身体,力量较大,最多能提起m=50kg 的物体。
一重物放置在倾角θ=15°的粗糙斜坡上,重物与斜坡间的摩擦因数为μ=33≈0.58。
试求该同学向上拉动的重物质量M 的最大值? 【答案】70.7kg 【解析】设该同学拉动重物的力F 的方向与斜面成角度φ,根据力的平衡,在垂直于斜面的方向上有F N +F sin φ-Mg cos θ=0 ①式中F N 是斜面对重物的支持力,其大小等于重物对斜面的正压力。
沿斜面的方向上有F cos φ-μF N - Mg sin θ=Ma ②根据题意,重物刚能被拉动,加速度a 近似为零,由牛顿运动定律F cos φ-μF N - Mg sin θ=0 ③联立①③式得 θθμϕμϕsin cos sin cos ++⋅=g F M ④ 令Ω=tan μ⑤ 联立④⑤式得)sin()cos(Ω+-Ω⋅=θϕg F M ⑥ 要使质量最大,分子须取最大值,即1)cos(=-Ωϕ,ϕ=Ω⑦ 此时能拉动的重物的质量的最大值为 )sin(1Ω+⋅=θg F M max ⑧ 由题给数据,知33tan =Ω,︒=Ω30⑨ 于是该同学能拉动的重物质量不超过M max ,有 kg 7.702)1530sin(1≈=︒+︒⋅=<m g mg M M max ⑩ 评分参考:①②式各3分,得到⑦式5分,得到⑩式4分。
【知识点】静力学拓展 【难度系数】4【试题来源】2011复旦大学自主招生【题目】2、如图所示,竖直杆AB 在细绳AC 的拉力作用下处于平衡。


巧用摩擦角解决高考力学中的极值与临界问题作者:陈远奎来源:《读天下》2017年第21期摘要:巧妙利用摩擦角解决高考力学中的有关摩擦力的极值和临界问题。
关键词:摩擦角;高考试题;极值与临界问题摩擦角是力学中的一个基本概念,它是研究摩擦问题的另一个重要物理量。
灵活运用摩擦角及其相关知识,可以巧妙解决有关摩擦的力学问题。
下面结合几道高考物理力学中的极值与临界问题,就摩擦角的相关概念及其应用做一介绍。
一、摩擦角简介1. 全反力是物体所受的支持力N与摩擦力fk的合力。
2. 滑动摩擦角用φk表示(如图1所示),其大小由动摩擦因素来决定,tanφk=fkN=μ,在实际问题中,虽然全反力随外力大小发生变化,但方向不变。
3. 静摩擦角用φs表示(如图2所示),其大小满足tanφs=fsN,当物体处于滑动的临界状态时,静摩擦力fs达到最大值fsm,对应的夹角也达到最大值φsm,其值由静摩擦因数决定,tanφsm=fsmN=μs。
高中阶段认为φsm=φk。
二、拉力的极小值【例1】(2013山东卷22)如图3所示,一质量m=0.4kg的小物块,以v0=2m/s的初速度,在与斜面成某一夹角的拉力F作用下,沿斜面向上做匀加速运动,经t=2s的时间物块由A点运动到B点,A、B之间的距离L=10m。
已知斜面倾角θ=30°,物块与斜面之间的动摩擦因数μ=33。
重力加速度g取10m/s2。
(1)求物块加速度的大小及到达B点时速度的大小。
(2)拉力F与斜面的夹角多大时,拉力F最小?拉力F的最小值是多少?解析:(1)略(2)对物体受力分析,如图4所示,先研究支持力FN与摩擦力f的合力,即为全反力F 全。
则有∠1=arctanfFN=arctanμ=30°。
现将其中支持力FN与摩擦力f用全反力F全来等效替代。
根据矢量运算法则,平移全反力F全至与重力mg首尾相接,如图5所示。
又依题意知,所受外力的合力F合为一定值,所以由图5可知,只有当拉力F垂直全反力F全时取得最小。

巧用摩擦角求解极值问题
发表时间:2012-03-06T09:39:57.133Z 来源:《学习方法报·理化教研周刊》2012年第34期供稿作者:陈永宁[导读] 动摩擦力与支持力的合力与水平方向的夹角为定值,这个角就称为摩擦角陕西省宝鸡市扶风县扶风高中陈永宁
什么是摩擦角?当一个质量为m的物体在动摩擦因数为的水平面上运动时,这个物体受到的支持力总是和动摩擦力垂直。
如图1所示:
,可见当一定时,动摩擦力与支持力的合力与水平方向的夹角为定值,这个角就称为摩擦角。
有这样一道题:一个重10 N的物体沿动摩擦因数的水平面上匀速运动,求所加拉力的最小值。
()解法一物体受力如图2所示:
匀速运动时,则拉力等于摩擦力:
解法二我们知道了摩擦角就可以运用图解法求解。
我们先做出受力分析:
在受力图3上将动摩擦力和支持力合称为一个方向确定的力,此四力问题就可转化为三力平衡问题:一个重力,其大小和方向确定;一个方向确定的力——动摩擦力和支持力的合力;第三个力未知。
符合图解法求解条件,为此我们用图解法求解,由几何作图4就可知:当拉力与支持力和动摩擦力的合力垂直时拉力最小。
也就是说当拉力与水平方向的夹角等于摩擦角时拉力最小。
即
细心的读者,你说哪种方法正确呢?(方法二正确)。

摩擦力与静力学力的平衡与运动状态的探索摩擦力与静力学力是物体在运动中产生的两种相互作用力。
在许多日常生活和工业应用中,我们常常会遇到需要平衡这两种力以保持物体的稳定性或实现预期动作的情况。
本文将探讨摩擦力与静力学力之间的关系以及它们对物体的运动状态产生的影响和调节。
摩擦力是两个物体之间接触表面上产生的力,它的存在常常导致物体在运动过程中减速或停止。
摩擦力的大小与物体之间的接触面积、摩擦系数及施加在物体上的力的大小相关。
静力学力是物体受力平衡时的力,它包括对物体施加的垂直向下的重力以及垂直向上的支持力或正压力。
在静止状态下,当物体受到外力施加时,通过调节施加力的大小,我们可以平衡静力学力和摩擦力,使物体保持静止。
这种平衡的状态被称为静态平衡。
例如,当我们将书放在桌子上时,重力向下作用于书籍,而桌子提供的支持力向上抵消了重力。
此时,摩擦力阻碍了书籍下滑的运动,因此我们感觉到书籍是静止的。
然而,在某些情况下,当外力超过摩擦力和静力学力之和时,物体将开始运动。
这种平衡的状态被称为动态平衡。
例如,当我们推动一辆停放的自行车,刚开始由于摩擦力的作用,我们需要施加更大的外力才能克服静力学力和摩擦力。
一旦自行车开始运动,摩擦力的大小将减小,并且我们只需要施加相对较小的力来保持运动状态。
此外,摩擦力和静力学力也会对物体的运动状态产生影响。
在某些情况下,摩擦力可以使物体保持在平衡位置上,阻止其滑动或滚动。
例如,当我们将一个能滑动的方块放在斜坡上时,由于摩擦力的存在,方块将保持在原地不滑下斜坡。
这种摩擦力称为静摩擦力。
只有当我们施加足够大的外力超过静摩擦力时,这个方块才会开始滑动。
然而,在某些其他情况下,摩擦力会使物体产生运动,例如当我们将一个已经运动的方块推动到斜坡上时,摩擦力将加速方块下滑的速度。
这种摩擦力被称为动摩擦力。
在这种情况下,摩擦力不再是平衡物体的力,而是加速或减缓物体运动的力。
总的来说,摩擦力和静力学力之间的平衡与物体的运动状态密切相关。
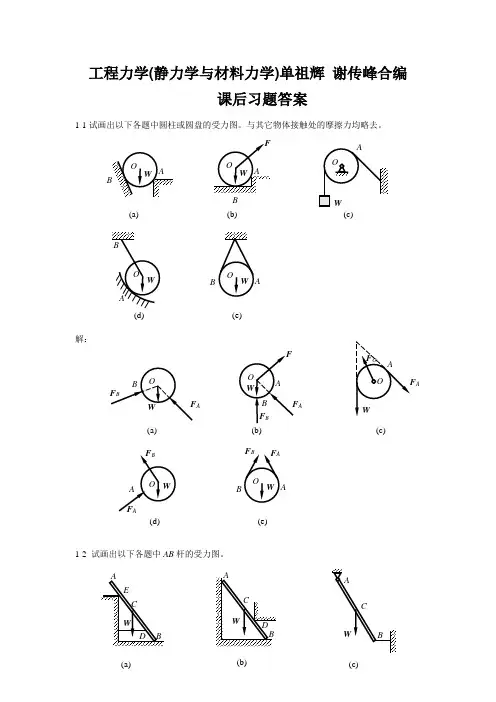
工程力学(静力学与材料力学)单祖辉 谢传峰合编课后习题答案1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解:1-2 试画出以下各题中AB 杆的受力图。
(a)(b)c)(d)A(e) A(a)(b) A(c)A(d)A(e)工程力学 静力学与材料力学 (单辉祖 谢传锋 著) 高等教育出版社 课后答案 解:1-3 试画出以下各题中AB 梁的受力图。
(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)解:1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ;(b) 半拱AB 部分;(c) 踏板AB ;(d) 杠杆AB ;(e) 方板ABCD ;(f) 节点B 。
解:(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)DBF D1-5 试画出以下各题中指定物体的受力图。
(a) 结点A ,结点B ;(b) 圆柱A 和B 及整体;(c) 半拱AB ,半拱BC 及整体;(d) 杠杆AB ,切刀CEF 及整体;(e) 秤杆AB ,秤盘架BCD 及整体。
(d)FC(e)WB(f)F FBC(c)(d)(b)e)解:(a)(b)(c)(d)(e)ATF BAFCAA C’CDDC’B2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点C 为研究对象,画受力图,注意AC 、BC 都为二力杆,(2) 列平衡方程:12140 sin 600530 cos 6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点,如图所示。
如不计刚架重量,试求支座A 和D 处的约束力。
力学12(摩擦角公式)1.摩擦角、滑动摩擦问题中的不变量:(高考范围一般把最大静摩擦力等于滑动摩擦力,故静摩擦角等于动摩擦角)①摩擦角=弹力与滑动摩擦力的合力的夹角;滑动摩擦力与弹力成对出现、合力的方向固定,利用°摩擦角线”可以巧妙解决滑动摩擦相关受力分析;②技巧:主要是隔离法的运用。
题目问物块,就隔离物块;问地面和斜面的作用力,就隔离斜面。
③注意:一定要是滑动摩擦才有摩擦角线。
1.如图所示,一斜面体静止在粗糙的水平地面上,一物体恰能在斜面体上沿斜面匀速下滑。
若沿平行于斜面的方向用力F 向下推此物体,使物体加速下滑,斜面体依然和地面保持相对静止,则斜面体受地面的摩擦力( )A. 大小为零B. 方向水平向右C. 方向水平向左D. 大小和方向无法判断2.如图所示,放在斜劈上的物块,受到平行于光滑斜面向下的力F作用,沿斜面向下运动,斜劈保持静止。
下列说法正确的是()A.地面对斜劈的摩擦力方向水平向右B.地面对斜劈的弹力大于斜劈和物块的重力之和C.若F增大,地面对斜劈的摩擦力也增大D.若F反向,地面对斜劈的摩擦力也反向3.(多选)如图所示,质量为m的物体恰能在一个斜面体上沿斜面匀速下滑,而斜面体处于静止状态,下列叙述中正确的是()A. 斜面体受地面的摩擦力为0B. 若仅沿斜面方向用力向下推物体,使物体加速下滑,而斜面体仍处于静止状态,则斜面体受地面的摩擦力方向水平向右C. 若仅增大斜面倾角,使物体加速下滑,而斜面体仍处于静止状态,则斜面体受地面的摩擦力方向水平向左D. 若仅减小斜面倾角,使物体减速下滑,而斜面体仍处于静止状态,则斜面体受地面的摩擦力力向水平向右4.如图所示,水平地面上有楔形物体b,b的斜面上有一小物块a,a与b之间、b与地面之间均存在摩擦。
已知a恰好可沿斜面匀速下滑,此时若对a施加如图所示的作用力,a仍沿斜面下滑,则下列说法正确的是( )A. 在a上施加竖直向下的力F1,则地面对b摩擦力水平向左B. 在a上施加沿斜面向下的力F2,则地面对b的摩擦力水平向左C. 在a上施加一个水平向左的力F3,则地面对b的摩擦力水平向右D. 无论在a上施加什么方向的力,地面对b均无摩擦力5.如图所示,斜面体A放置在水平地面上,当只有小物体B放在斜面体上沿斜面体匀速下滑,此时斜面体A受到地面的摩擦力为f1,受到地面的支持力为N1.当用沿如图所示方向平行斜面向下的力F向下推此物体,使物体沿斜面匀加速下滑,此时斜面体A受地面的摩擦力为f2,受到地面的支持力为N2,斜面体始终静止在地面,则()A.f1=0 f2=0 N1=N2 B.f1=0 f2≠0 N1>N2B.f1≠0 f2=0 N1>N2 D.f1≠0 f2≠0 N1<N26.如图所示,斜面体A放置在水平地面上,当只有小物体B放在斜面体上沿斜面体匀速下滑,此时斜面体A受到地面的摩擦力为f1,受到地面的支持力为N1.当用沿如图所示方向平行斜面向上的力F向上推此物体,使物体沿斜面匀速上滑,此时斜面体A受地面的摩擦力为f2,受到地面的支持力为N2,斜面体始终静止在地面,则()C.f1=0 f2=0 N1=N2 B.f1=0 f2≠0 N1>N2D.f1≠0 f2=0 N1>N2 D.f1≠0 f2≠0 N1<N27.在粗糙水平面上有一个三角形物块,在它的两个粗糙斜面上分别放两个质量为m1和m2的木块,m1>m2,θ1<θ2.已知两斜面均能沿斜面匀速下滑。
静力学平衡△处理静力学平衡问题的三种巧妙方法: ※巧用矢量图解1.如图所示,三角形ABC 三边中点分别为D 、E 、F ,在三角形中任取一点O ,如果DO 、OE 、OF 三个矢量代表三个力,那么这三个力的合力为多少? 解:如图所示:因为DO OE DE +=,12DE AB FA ==,OF FA OA +=,所以DO OE OF OA ++=,则这三个力的合力F OA ∑=。
2.如图所示,一个重为G 的小环,套在竖直放置的半径为R 的光滑大圆环上.有一劲度系数为k ,自然长度为L (L <2R )的轻弹簧,其上端固定在大圆环的最高点A ,下端与小环相连,不考虑一切摩擦,则小环静止时弹簧与竖直方向的夹角θ为多大?解:由几何关系知,cos 2L lRθ+∆= ①由力的矢量三角形与几何三角形相似得;k l G L l R ⋅∆=+∆,Gl L kR G ∆=- ② 联立①②得: cos 2()kRLR kR G θ=-,arccos2()kLkR G θ=-3. 如图所示,倾角为θ的斜面与水平面保持静止,斜面上有一重为G 的物体A 与斜面间的动摩擦因数为μ,且tan μθ<,现给A 施以一水平力F ,设最大静摩擦力与滑动摩擦力相等,求水平推力F 多大时物体能地斜面上静止? 解:静摩擦力达到最大时,斜面约束力作用线方向与斜面法线成摩擦角。
max tan(arctan )F mg θμ=+ ①min tan(arctan )F mg θμ=- ②联立①②得:sin cos sin cos cos sin cos sin F θμθθμθθμθθμθ-+≤≤+-4.如图所示,放在水平面上的质量为m 的物体,在水平恒力1F 作用下,刚好做匀速直线运动.若再给物体加一个恒力,且使1F =2F ,要使物体仍按原方向做匀速直线运动,力2F 应沿什么方向?此时地面对物体的作用力大小如何? 解:水平恒力与重力、地面约束力作用而平衡时,三力构成闭合三角形;加2F 仍构成闭合三角形:2111F F μμμ+-=地;2111F F μμμ++=地。
用摩擦角巧解静力学问题
摘要:在高中物理竞赛中常遇到静力学问题,计算量比较大,将常规方法与应用摩擦角和全反力解题进行比较,便体现应用摩擦角解题的优势。
关键词:摩擦角;全反力;物体的平衡什么是摩擦角?当两物体相互接触,如图1,接触面之间有摩擦时,支持面对物体具有支持力N和摩擦力f的作用,这两个力的合力称为全反力,其作用线与支持面的垂线即支持力的作用线之间形成的偏角为?渍,当达到临界平衡状态时,静摩擦力达到最大值,偏角j也达到了最大值?渍m,如图2所示,全反力与支持力之间夹角的最大值被称为摩擦角,由图可知tan ?渍m== μ,?渍m 与μ表明物体之间的摩擦性质。
由摩擦角的定义可以知道,全反力的作用线不可能超出摩擦角之外,必在摩擦角之内。
因此,一定存在0≤?渍≤?渍m 。
下面通过例题来说明全反力和摩擦角在解决静力学问题中的优势。
例题:如图3所示,质量为m的物体恰好能在倾角为α的固定斜面上匀速下滑,如在物体上施加一个力使物体沿斜面匀速上滑,为了使力取得最小值,这个力与斜面的倾斜角为多大?这个力的最小值是多少?解:物理情境I:由物体恰好能在斜面上匀速下滑,受力分析如图4,列方程mg sin a =μmg cos α可得μ= tan α。
物理情境II:对物体施加力F,使物体沿斜
面匀速上滑,求F的最小值,可有两种方法。
方法一:数学极值法:受力分析如图5所示,设力F与斜面之间的夹角为θ,因为物体是匀速运动,处于平衡状态,物体所受的合外力为0。
列平衡方程如下:沿斜面方向:F cos θ= mg sin α+f
①垂直于斜面:F sin θ+N = mg cos α
②
f= μN
③由①、②、③得:F = mg 要使F取最小值,只要使表达式取最大值,该表达式可以表示为:cos θ+μsin θ= sin (?渍+θ)
④其中取sin ?渍= ,cos ?渍=
由④式可得,当时sin(?渍+θ)=1时,即?渍+θ= 90°时,F为最小,此时tan ?渍= ,?渍= arctan,即:当θ= 90°-?渍= arctan μ=α时,F具有最小值,其最小值为:F=mgsin(θ+α)=mgsin2a,F= mg =(sin αsin ?渍+ cos αcos ?渍)mg =2 sin αcos ?渍mg = mg sin 2α。
方法二:受力分析如图6所示,物体受重力mg、全反力F反(支持力N与摩擦力f的合力,且摩擦角?渍= arctan = arctan μ= α)和F,相当于物体在三个力的作用下处于平衡状态,F反、F的合力与mg大小相等方向相反,画出平行四边形。
从图上可以看出,当F与F反垂直时,F取最小值,θ= 90°-α-(90°-α-?渍)= α。
则F=mg sin(?渍+α)=mg sin 2α,F与重力的夹角为90°- 2α,与斜面的夹角为θ=90°-α-(90°-α)=α。
点评:方法一是根据物体的平衡条件,建立坐标系列方程,对学生来说思路比较顺畅,但是对数学知识的要求很高。
方法二引入了全反力与摩擦角,利用三力平衡的知识做矢量三角形求其最值,有很强的技巧性,数学要求低,且容易计算。
两种方法比较,显然方法二要简单得多。
总之,在解决静力学问题时,恰当地使用摩擦角和全反力可以起到事半功倍的效果。
编辑杨倩。