下载文档原格式
第2章 杆件的拉伸与压缩提要：轴向拉压是构件的基本受力形式之一，要对其进行分析，首先需要计算内力，在本章介绍了计算内力的基本方法——截面法。
为了判断材料是否会发生破坏，还必须了解内力在截面上的分布状况，即应力。
由试验观察得到的现象做出平面假设，进而得出横截面上的正应力计算公式。
根据有些构件受轴力作用后破坏形式是沿斜截面断裂，进一步讨论斜截面上的应力计算公式。
为了保证构件的安全工作，需要满足强度条件，根据强度条件可以进行强度校核，也可以选择截面尺寸或者计算容许荷载。
本章还研究了轴向拉压杆的变形计算，一个目的是分析拉压杆的刚度问题，另一个目的就是为解决超静定问题做准备，因为超静定结构必须借助于结构的变形协调关系所建立的补充方程，才能求出全部未知力。
在超静定问题中还介绍了温度应力和装配应力的概念及计算。
不同的材料具有不同的力学性能，本章介绍了塑性材料和脆性材料的典型代表低碳钢和铸铁在拉伸和压缩时的力学性能。
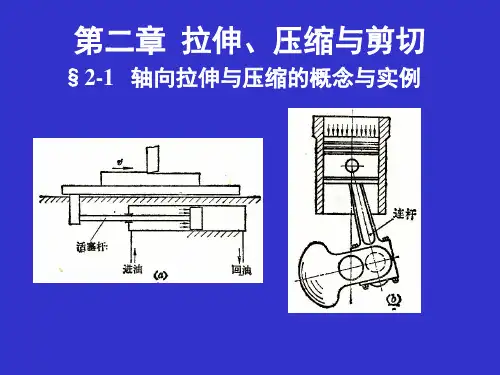
2.1 轴向拉伸和压缩的概念在实际工程中，承受轴向拉伸或压缩的构件是相当多的，例如起吊重物的钢索、桁架第2章 杆件的拉伸与压缩 ·9··9·2.2 拉(压)杆的内力计算2.2.1 轴力的概念为了进行拉(压)杆的强度计算，必须首先研究杆件横截面上的内力，然后分析横截面上的应力。
下面讨论杆件横截面上内力的计算。
取一直杆，在它两端施加一对大小相等、方向相反、作用线与直杆轴线相重合的外力，使其产生轴向拉伸变形，如图2.2(a)所示。
为了显示拉杆横截面上的内力，取横截面把m m −拉杆分成两段。
杆件横截面上的内力是一个分布力系，其合力为N F ，如图2.2(b)和2.2(c)所示。
由于外力P 的作用线与杆轴线相重合，所以N F 的作用线也与杆轴线相重合，故称N F 为轴力(axial force)。
由左段的静力平衡条件0X =∑有：()0+−=N F P ，得=N F P 。
第2章拉伸、压缩与剪切2.1本章要点详解本章要点■轴力的计算和轴力图的绘制■典型塑性和脆性材料的主要力学性能及相关指标■横截面上的应力计算、拉压强度条件及计算■拉（压）杆的变形即桁架位移计算■拉压超静定的基本概念及超静定问题的求解方法■剪切变形的特点，剪切与挤压实用计算重难点导学一、轴向拉伸与压缩的概念和实例轴向拉伸与压缩的受力特点与变形特点：作用在杆件上的外力合力的作用线与杆件轴线重合，杆件变形是沿轴线方向的伸长或缩短，如图2-1所示。
图2-1二、轴向拉伸或压缩时横截面上的内力和应力1．轴力F N（1）定义轴力是指在外力F作用下，内力的合力F N，其作用线与轴线重合。
（2）符号规定把拉伸时的轴力规定为正，压缩时的轴力规定为负。
2．轴力图（1）定义轴力图是指选取一个坐标系，横坐标表示横截面的位置，纵坐标表示相应截面上的轴力，表示出轴力沿杆轴线变化情况的图形。
（2）注意事项拉力绘制在x轴上侧，压力绘制在x轴下侧。
3．应力（1）杆件的强度不仅与轴力有关，还与横截面面积有关。
因此必须用应力来比较和判断杆件的强度。
与轴力对应的是正应力。
（2）根据变形固体的基本假设和平截面假设，横截面上的正应力均匀分布且相等，而轴力是应力的合力，于是可得拉（压）杆横截面上正应力计算公式N F Aσ=（3）符号规定拉应力为正，压应力为负.（4）平截面假设变形前原为平面的横截面，变形后仍保持为平面且仍垂直于轴线。
三、直杆轴向拉伸或压缩时斜截面上的应力实验表明：拉（压）杆的破坏并不总是沿横截面发生，有时却是沿斜截面发生的。
由此可以计算与垂直方向夹角为α的斜面上的应力。
1．表达式轴向拉力F 作用下，横截面面积为A 的直杆，如图2-2所示。
（1）任意斜截面的总应力cos cos a F p Aασα==（2）垂直于斜截面的正应力2c o s ασσα=（3）相切于斜截面的切应力sin 22αστα=式中，α为斜截面与横截面的夹角，以横截面外向法线至斜截面外向法线为逆时针转向时为正，反之为负。
