二分法求解单变量非线性方程及其应用与实现(精)

二分法实验(1)上机题目：二分法的应用实验目的：熟悉二分法并在计算机上实现实验要求：①上机前充分准备，复习有关内容，写出计算步骤，查对程序；②完成实验后写出完整的实验报告，内容应该包括：所用的算法语言，算法步骤陈述，变量说明，程序清单，输出计算结果，结果分析等等；③用编好的程序在Ｍatlab 环境中执行。

算法说明：①找出 计算f(x)在有限根区间[a, b]端点的值，f(a),f(b)②计算 计算f(x)在区间中点（2b a +）处的值f(2b a +) . ③判断 若f(2b a +)=0，则2b a +即是根，计算过程结束，否则检验若(2b a +)f(a)<0，则以2b a +代替b,否则以2b a +代替a.反复执行步骤②和步骤③，直到区间[a, b]长度小于允许误差ξ，此时中点2b a +即为所求近似根。

计算例题：求f (x )=x 3- x -1在[1,1.5]的零点. f (1)<0,. f (1.5)>0,delta= d=106-不动点迭代法实验⑵上机题目：不动点迭代法的实现实验目的：熟悉迭代法并在计算机上实现实验要求：①上机前充分准备，复习有关内容，写出计算步骤，查对程序；②完成实验后写出完整的实验报告，内容应该包括：所用的算法语言，算法步骤陈述，变量说明，程序清单，输出计算结果，结果分析等等；③用编好的程序在Ｍatlab 环境中执行。

算法说明：①准备 将0)(=x f 改写为等价的形式)(x x ϕ=。

若要求*x 满足0)(*=x f ，则)(**x x ϕ=；反之亦然。

求)(x f 的零点，等价于求的不动点，选择一个初始近似值0x 代入)(x x ϕ=右端，得)(01x x ϕ=。

如此反复迭代计算⋯==+,1,0),(1k x x k k ϕ，此为迭代公式。

②不动点的存在性迭代法的收敛性定理1 设],[)(b a C x ∈ϕ满足：(1)对任意],[b a x ∈有b x a ≤≤)(ϕ;(2)存在正常数L<1，使对任意],[,b a y x ∈都有|||)()(|y x L y x -≤-ϕϕ，则)(x ϕ在],[b a 上存在唯一不动点*x 。

第七章非线性方程解法⒈二分法考察有根区间[a, b]，取中点x0=(b+a)/2 将它分为两半，假设中点x0不是f(x)的零点，然后进行根的搜索，即查找f(x0)与f(a)是否同号，如果确系同号，说明所求的根x*在x0的右侧，这是令a1= x0，b1=b;否则x*必在x0的左侧，这是令a1=a,b1=x0,不管出现哪一种情况，新的有根区间[a1, b1]的长度仅为[a, b]的一半。

.重复以上做法得新近似根x1,…这样不断将区间分半,得到一系列区间[an , bn],和近似根(区间中点)nx,n=0,1,2,3…,nx误差为(b-a)/2n+1.这样的方法称为二分法。

下面是一个关于二分法的例子。

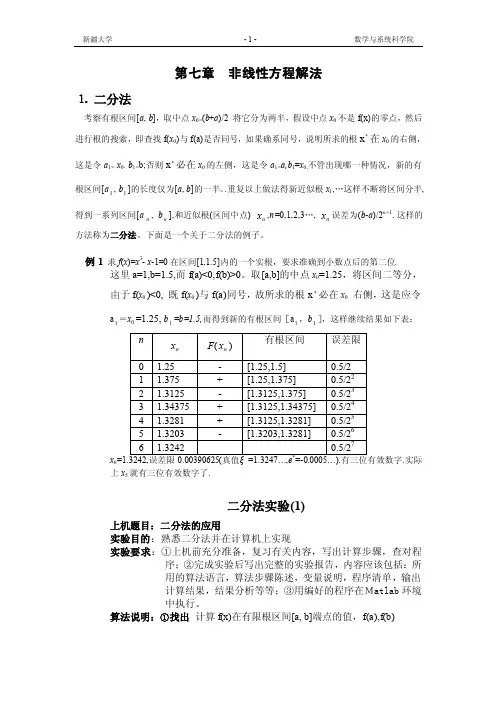
例1求f(x)=x3- x-1=0在区间[1,1.5]内的一个实根，要求准确到小数点后的第二位.这里a=1,b=1.5,而f(a)<0,f(b)>0。

取[a,b]的中点x0=1.25，将区间二等分，由于f(x0 )<0, 既f(x0 )与f(a)同号，故所求的根x*必在x0 右侧，这是应令a1＝x0 =1.25, b1=b=1.5,而得到新的有根区间［a1，b1］，这样继续结果如下表：x6.实际上x5就有三位有效数字了.二分法实验(1)上机题目：二分法的应用实验目的：熟悉二分法并在计算机上实现实验要求：①上机前充分准备，复习有关内容，写出计算步骤，查对程序；②完成实验后写出完整的实验报告，内容应该包括：所用的算法语言，算法步骤陈述，变量说明，程序清单，输出计算结果，结果分析等等；③用编好的程序在Ｍatlab环境中执行。

算法说明：①找出计算f(x)在有限根区间[a, b]端点的值，f(a),f(b)②计算计算f(x)在区间中点（2ba+）处的值f(2ba+) .③判断若f(2ba+)=0，则2ba+即是根，计算过程结束，否则检验若f(2ba+)f(a)<0,则以2ba+代替b,否则以2ba+代替a.反复执行步骤②和步骤③，直到区间[a, b]长度小于允许误差ξ，此时中点2ba+即为所求近似根。

1、编程实现以下科学计算算法，并举一例应用之（参考书籍《精通MATLAB 科学计算》，王正林等编著，电子工业出版社，2009年） “二分法非线性方程求解”二分法的具体求解步骤如下。

（1）计算函数f(x)在区间[a,b]中点的函数值f((a+b)/2)，并作下面的判断： 如果0)2()(<+ba f a f ，转到（2）； 如果0)2()(>+b a f a f ，令 2ba a +=，转到（1）； 如果 0)2()(=+b a f a f ，则 2ba x +=为一个跟。

（2）如果 ε<+-|2|b a a （ε为预先给定的精度），则43ab x +=为一个根，否则令2ba b +=，转到（1）。

在MATLAB 中编程实现的二分法函数为：HalfInterval 。

功能：用二分法求函数在某个区间上的一个零点。

调用格式：root=HalfInterval(f,a,b,eps). 其中，f 函数名； a 为区间左端点； b 为区间右端点；eps 为根的精度； root 为求出的函数零点。

二分法的MATLAB 程序代码如下：function root=HalfInterval(f,a,b,eps) %二分法求函数f 在区间[a,b]上的一个零点 %函数名：f %区间左端点：a %区间右端点：b %根的精度：eps %求出的函数零点：root if (nargin==3) eps=1.0e-4;endf1=subs(sym(f),findsym(sym(f)),a); %两端点的函数值f2=subs(sym(f),findsym(sym(f)),b);if(f1==0)root=a;endif(f2==0)root=b;endif(f1*f2>0)disp('两端点函数值乘积大于0!');return;elseroot=FindRoots(f,a,b,eps); %调用求解子程序endfunction r=FindRoots(f,a,b,eps)f_1=subs(sym(f),findsym(sym(f)),a);f_2=subs(sym(f),findsym(sym(f)),b);mf=subs(sym(f),findsym(sym(f)),(a+b)/2); %中点函数值if(f-1*mf>0)t=(a+b)/2;r=FindRoots(f,t,b,eps); %右递归elseif(f_1*mf==o)r=(a+b)/2;elseif(abs(b-a)<=eps)r=(b+3*a)/4; %输出根elses=(a+b)/2;r=FindRooots(f,a,b,eps); %左递归endendend流程图：实例应用：采用二分法求方程0133=+-x x 在区间[0，1]上的一个根。

非线性方程的数值解法中的二分法
二分法，又称秦九韶算法，是一种用来求解非线性方程的有效的数值解法。

它可以有效地将一个不确定的区间划分为两个不相交的子区间，其中一个至少包含方程的一个根，而另一个不包含根，这样重复地使用子区间，就可以缩小包含根的子区间从而求出根。

它具有准确性好、计算量小、理论考虑简单等优点。

因此，二分法逐渐得到了在互联网科技领域的广泛应用，受到了更多关注。

作为一种基础性的数学算法，二分法的基本原理是将一个不确定的区间分成两个相等的小区间，其中一个必定包含方程的一个根，而另一个肯定不包含根，然后针对这两个相邻区间，不断求解，直到最后已经求出根为止。

具体地说，在给定一个区间[a，b]，要求函数f (x)在[a，b]内存在唯一根r，根据贴合定理，只需要计算函数在两个端点的值，并判断它们是否异号，如果异号，则区间[a，b]一定包含根r。

接着，利用c =(a＋ b) / 2将区间[a，b]分成两个小区间[a，c]和[c，b]，逐渐缩小根所在的区间范围，直到最后确定根的准确值。

由于数值计算的准确性高、计算量小、计算过程简单，因此二分法在许多互联网科技应用中大量采用，如自动搜索引擎服务，精准推荐等。

此外，在建模和科学研究中，二分法也被广泛运用，例如求解非线性方程组、解析一元函数最优解等。

综上所述，二分法是一种有效的数值解法，在互联网科技的应用非常广泛，如搜索引擎服务、精准推荐以及科学研究等，它具有计算准确度高、计算量小、理论需要考虑较少的优势，有效地解决非线性方程的求解问题，同时也为科技进步和科学发展作出了贡献。

非线性方程求解在数学中，非线性方程是一种函数关系，其表达式不能通过一次函数处理得到。

与线性方程不同，非线性方程的解决方案往往更具挑战性，因为它涉及到更复杂的计算过程。

尤其在实际应用中，非线性方程的求解是一个非常重要的问题。

本文将讨论几种常用的非线性方程求解方法。

二分法二分法，也称为折半法，是一种基本的求解非线性方程的方法之一。

它的核心思想是将区间一分为二并判断方程在哪一半具有根。

不断这样做直到最终解得精度足够高为止。

下面是利用二分法求解非线性方程的流程：1. 设定精度值和区间范围2. 取区间的中点并计算函数值3. 如果函数值为0或函数值在给定精度范围内，返回中点值作为精确解4. 如果函数值不为0，则判断函数值的正负性并缩小区间范围5. 重复步骤2-4直到满足给定精度为止当然，这种方法并不总是能够找到方程的解。

在方程存在多个解或者区间范围不合适的情况下，二分法可能会导致求解失败。

但它是一种很好的起点，同时也是更复杂的求解方法中的一个重要组成部分。

牛顿迭代法牛顿迭代法是一种更复杂的求解非线性方程的方法。

它利用泰勒级数和牛顿迭代公式，通过不断迭代来逼近根的位置。

下面是利用牛顿迭代法求解非线性方程的流程：1. 先取一个近似值并计算函数值2. 求出函数的导数3. 利用牛顿迭代公式，计算下一个近似根4. 检查下一个近似根的精度是否满足条件，如果满足，返回当前近似根5. 如果精度不满足，则将新的近似根带入公式，重复步骤2-5当然，牛顿迭代法的收敛性并不总是保证的。

如果迭代过程太过温和，它可能无法收敛到精确解。

如果迭代过程过于暴力，则会出现发散现象，使得求解变得不可能。

其他方法此外，还有一些其他的求解非线性方程的方法，例如黄金分割法、逆二次插值法、牛顿切线法等等。

其中每一种方法都有其优缺点，不同的情况下，不同的方法都可能比其他方法更加适合。

结论总体来说，求解非线性方程的方法非常复杂。

无论是哪种方法，都需要一定的数学基础和计算机知识。

• 本章介绍方程的迭代解法，它既可以用来求解 代数方程，也可以用来解超越方程，并且仅限 于求方程的实根。
• 运用迭代法求解方程的根应解决以下两个问题：
• 确定根的初值; • 将进一步精确化到所需要的精度。
记笔记 第3页/共52页
7.1 二分法
二分法又称二分区间法,是求解非线性方程的近 似根的一种常用的简单方法。
第4页/共52页
确定有根区间的方法
• 为了确定根的初值，首先必须圈定根所在的范围，
称为圈定根或根的隔离。
• 在上述基础上，采取适当的数值方法确定具有一 定
精度要求的初值。
• 对于代数方程，其根的个数（实或复的）与其次 数
相同。至于超越方程，其根可能是一个、几个或
无
第5页/共52页
由高等数学知识知, 设f (x)为区间[a,b]上的 单值连续, 如果f (a)·f (b)<0 , 则[a,b]中至少 有一个实根。如果f (x)在[a,b]上还是单调地递 增或递减，则仅有一个实根。
二分法求根过程
设方程f(x)=0在区间[a,b]内有根,二分法就是逐 步收缩有根区间，最后得出所求的根。具体过程如下
① 取有根区间[a,b]之中点, 将它分为两半,分点
x0
ab 2
,这样就可缩小有根区间
y
y=f(x)
y=f(x)
a
x1
x* x0
a1
b1
a2
b2
b
a
第13页/共52页
x*
x0
x1
b
a1
再将 x1 代入式 x (x) 的右端, 得到 x2 (x1) , 依此类推, 得到一个数列 x3 (x2 ) …， 其一般表示

1 条件 f ( x) C[a,b],且f (a) f (b) 0
2 主要依据 由连续函数介值定理,则至少存在某个 x* (a,b),
使得f ( x* ) 0,即[a,b]内至少有方程(2.1)的一个根,称[a,b]为f(x)
的一个含根区间。并且有
x* a b b a
有根区间 中点 x n
-(1,2)+ (1,1.5)
x1 1.5 x2 1.25
(1.25,1.5)
x3 1.375
(1.25,1.375) x4 1.313
(1.313,1.375) x5 1.344
(1.344,1.375) x6 1.360
(1.360,1.375) x7 1.368
bk
生成含根区间[ak 1,bk 1] ,满足（2.2）式，即

(1) [ak 1 , bk 1 ] [ak h
(2) bk1 akak1 ak bk1 xk
x
(3) f (ak 1 ) f (bk 1 ) 0
含根区间 [ak 1,bk 1] 满足（2.2）式，即
对
区((间12))[找 a计k ,中算bk点](:,(23f)：)kbif令(xafaki ()ixkf12（ )(2(bhiai即)1k,中 i0b,k点 i0);,的 10,,1函,,数 k,,k值. ）; (3) 生成含根区间：
(2.2)
ak ak
x* xk xk
若f ( x1 ) 0，则x* x1 ,
若f ( x1 ) f (a1 ) 0, 取a2 x1, b2 b1, 若f ( x1 ) f (a1 ) 0, 取a2 a1, b2 x1,

end 程序输出
n=01,当前有根区间是[0.000000,0.500000],近似根为 0.500000,wucha=0.500000 n=02,当前有根区间是[0.250000,0.500000],近似根为 0.250000,wucha=0.250000 n=03,当前有根区间是[0.250000,0.375000],近似根为 0.375000,wucha=0.125000 n=04,当前有根区间是[0.250000,0.312500],近似根为 0.312500,wucha=0.062500 n=05,当前有根区间是[0.250000,0.281250],近似根为 0.281250,wucha=0.031250 n=06,当前有根区间是[0.265625,0.281250],近似根为 0.265625,wucha=0.015625 n=07,当前有根区间是[0.265625,0.273438],近似根为 0.273438,wucha=0.007813 n=08,当前有根区间是[0.265625,0.269531],近似根为 0.269531,wucha=0.003906 n=09,当前有根区间是[0.265625,0.267578],近似根为 0.267578,wucha=0.001953 n=10,当前有根区间是[0.265625,0.266602],近似根为 0.266602,wucha=0.000977 n=11,当前有根区间是[0.266113,0.266602],近似根为 0.266113,wucha=0.000488 n=12,当前有根区间是[0.266113,0.266357],近似根为 0.266357,wucha=0.000244 n=13,当前有根区间是[0.266235,0.266357],近似根为 0.266235,wucha=0.000122 n=14,当前有根区间是[0.266235,0.266296],近似根为 0.266296,wucha=0.000061 n=15,当前有根区间是[0.266235,0.266266],近似根为 0.266266,wucha=0.000031 n=16,当前有根区间是[0.266235,0.266251],近似根为 0.266251,wucha=0.000015 n=17,当前有根区间是[0.266243,0.266251],近似根为 0.266243,wucha=0.000008 n=18,当前有根区间是[0.266247,0.266251],近似根为 0.266247,wucha=0.000004 n=19,当前有根区间是[0.266247,0.266249],近似根为 0.266249,wucha=0.000002 n=20,当前有根区间是[0.266248,0.266249],近似根为 0.266248,wucha=0.000001

＇ ２
求解方程的近似根 ， 一般需要解决两个问题 ： １ ． 根 的隔离 。即找 出有根 区域 ， 使得在一些小 区间中 方程只有一根（ 或一对共轭复根 ） 以便获取各根的较粗糙 的近似值 。
区间值 ：ｘ ０
０ ． ０ ０ Ｏ Ｏ ０ ０ ０ ０ ０ ０ ０ ０ Ｏ ０ Ｏ ． ０ Ｏ Ｏ ０ ０ Ｏ ０ ０ ０ Ｏ ０ ０ ０ ０
【 专题研讨 】
二分法和牛顿迭代法 求解非线性 方程 的比较及应用
张 晓勇 ， 王 仲君
（ 武汉 理工 大学 ， 湖北 武汉 ４ 文基于计算机ＭＡ Ｔ Ｌ Ａ Ｂ 和ｃ 语 言编程去分析 两者的计算复杂性 ， 并深入探讨 了两种方法的优缺点。 最后 ， 通 过将 两种方法结合起来解决非线性方程 的求解问题 ， 取得 了显著地效果 。同时， 这也再 次证明 了方法组合解决问题 的高
一
、
２ ０
２ １
５ ２ ． ４ ０ ６ ３ １ １ ０ ０ ０ ０ ０ ０ ０
５ ２ ． ４ ０ ６ ７ ８ ８ Ｏ Ｏ ０ ０ Ｏ ０ ０
５ ２ ． ４ ０ ７ ２ ６ ５ Ｏ ０ ０ Ｏ ０ ０ ０
效性 。
关键词 ： 二分法； 牛顿迭代法 ； 非线性 方程 中图 分 类 号 ： ０２ ４ ２ 文 献 标 志码 ： Ｂ
文 章编 号 ： １ ６ ７ ４ — ９ ３ ２ ４ （ ２ ０ １ ３ ） ２ ５ — ０ １ ３ ９ 一 Ｏ １
表１ 二 分法 程序 结 果
迭 代 数
区 间值 ：ｘ １
５ ０ ０ ． Ｏ ０ Ｏ Ｏ ０ ０ ０ ０ ０ Ｏ ０ ０ ０ ２ ５ ０． ０ ０ ０ ０ ０ ０ Ｏ ０ ０ ０ ０ ０ ０
２ ． 近似根 的精确化 。即用求根的数值方法 ， 使求得 的 近似根逐步精确化 ， 直到获得一定精度的近似根。 二分法和牛顿迭代法的基本思想 １ ． 二分法 。一般地 ， 对于 函数ｆ （ ｘ ） ， 如果存在实数Ｃ ， 当 Ｘ ＝ Ｃ 时， 若ｆ （ ｃ ） ＝ ０ ， 那么把ｘ ＝ ｃ Ｈ ｑ 做函数ｆ （ ｘ ） 的零点。解方程 即要求 ｘ ） 的所有零点。假定ｆ （ ｘ ） 在 区间（ ｘ ， ｙ ） 上 连续 ， 先 找到ａ 、 ｂ 属于区间（ ｘ ， Ｙ ） ， 使ｆ （ ａ ） ， ｆ （ ｂ ） 异号 ， 说 明在 区间（ ａ ， ｂ ） 内一定有零点 ， 然后求［ ｆ （ ａ ＋ ｂ ） ／ ２ １ ， 现在假设ｆ （ ａ ） ＜ ０ ， ｆ （ ｂ ） ＞ ０ ， ａ ＜ ｂ ， ①如果［ ｆ （ ａ ＋ ｂ ） ／ ２ ］ ＝ Ｏ ， 该点就是零点。 如果［ ｆ （ ａ ＋ ｂ ） ／ ２ ］ ＜ Ｏ ， 则在 区间（ （ ａ ＋ ｂ ） １ ２ ， ｂ ） 内有零点 ， 注： （ ａ ＋ ｂ ） ／ ２ ＞ ＝ ａ ， 从① 开始继续使用 中点函数值判断。如果 ［ ｆ （ ａ ＋ ｂ ） ／ ２ 】 ＞ ０ ， 则在区 间（ ａ ， （ ａ ＋ ｂ ） １ ２ ） 内有零点 ， 注： （ ａ ＋ ｂ ） ／ ２ ＜ ＝ ｂ ， 从①开始继续使 用 中点 函数值判断。 这样就可以不断接近零点。 通过每次 把ｆ （ ｘ ） 的零点所在小区间收缩一半 的方法 ， 使 区间的两个 端点逐步迫近 函数的零点 ， 以求得零点 的近似值 ， 这种方 法叫做二分法 。 从以上可以看出 ， 每次运算后 ， 区间长度减 少一半 ， 是线形收敛 。另外 ， 二分法不能计算复根和重根 。 ２ ． 牛顿迭代法。设ｒ 是 ｘ ） ＝ ０ 的根 ， 选取ｘ ０ 作为ｒ 初始近 似值 ， 过点 （ ｘ Ｏ ， ｆ （ ｘ Ｏ ） ） 做 曲线ｙ ＝ ｆ （ ｘ ） 的切线 Ｌ ， Ｌ 的方程 为 ｙ ＝ ｆ （ ｘ Ｏ ） ＋ ｆ （ ｘ Ｏ ） （ ｘ — ｘ ０ ） ， 求 出Ｌ 与ｘ 轴交点 的横坐标ｘ ｌ ＝ ｘ Ｏ — ｆ （ ｘ Ｏ ） ／ ｆ （ ｘ Ｏ ） ， 称ｘ １ 为ｒ 的一次近似值。 过点（ ｘ ｌ ， ｆ （ ｘ １ ） ） 作 曲线 ｙ ＝ ｆ（ ｘ ）的切线 ，并求该切线与ｘ 轴交点 的横坐标ｘ ２ ＝ ｘ ｌ — ｆ （ ｘ １ ） ／ ｒ （ ｘ １ ） ， 称ｘ ２ 为ｒ 的二次近似值。重复 以上过程 ， 得ｒ 的 近似值序列 ， 其 中ｘ （ ｎ ＋ １ ） ＝ ｘ （ ｎ ） 一 ｆ （ ｘ （ ｎ ） ） （ ｘ （ ｎ ） ） ， 称为ｒ 的 ｎ ＋ １ 次近似值 ， 上式称为牛顿迭代公式 。 解非线性方程ｆ （ ｘ ） ０ 的牛顿法是把非线性方程线性化的一种近似方法 。把ｆ （ ｘ ） 在ｘ ０ 点附近展开成泰勒级数ｆ （ ｘ ） ＝ ｆ （ ｘ ０ ） ＋ （ ｘ — ｘ Ｏ ） ｒ （ ｘ Ｏ ） ＋ （ ｘ — ｘ Ｏ ） ＇ ２ ＊ ｆ ’ （ ｘ Ｏ ） ／ ２ １＋ …取其线性部分 ， 作为非线性方程ｆ （ ｘ ） ＝ ０ 的近似方程 ， 即泰勒展开的前两项 ， 则有ｆ （ ｘ Ｏ ） ＋ ｆ （ ｘ Ｏ ） （ ｘ — ｘ Ｏ ） ＝ ０ 设ｆ ＇ （ ｘ Ｏ ） ≠０ 则其解为ｘ ｌ ＝ ｘ Ｏ — ｆ （ ｘ Ｏ ） Ｘ（ ｘ Ｏ ） 这样 ， 得 到牛顿法 的一个迭代序列 ： Ｘ（ ｎ ＋ １ ） ＝ ｘ（ ｎ ） 一 ｆ（ Ｘ（ ｎ ） ） ／ ｒ （ ｘ （ ｎ ） ） ， 记为： ｛ ｘ （ ｎ ） ｌ 。 此时 ， 当ｎ 趋于无穷大时 ， ｘ （ ｎ ） 就会逐渐 逼近 ｘ ） ＝ ０ 的根。 二、 例证分析 １ ． 对此非线性方程ｘ Ｓ － ５ ０ ｘ Ｚ － ６ ６ １ ０ ＝ Ｏ 在单 独用二分法 和 牛顿迭代法时的效果都不显著。 实验 的结果分析： 由此可见 ， 牛顿迭代法是一种特殊 的迭代法 ， 用于求

2016/2017 学年
第一学期（16周）
二分法 – 非线性方程
二分法
原理：若 f C a, b ，且 f (a ) f (b) 0，则 f
在区间 (a,b) 上必须有一根。 考察：请求解三次元方程 f ( x) x 3 x 2 3 x 3 0 的正根？ 求解： f (1) 4 0, f (2) 3 0
*
计算方法（2016/2017 第一学期）
西南科技大学
制造科学与工程学院
4
二分法
在实际计算中，如果预先给定了精度 0 ，则
1 ba x xk bk ak k 1 2 2
*
当
达到了精度要求
ba k 1 2
* x x 时，则认为 k 作为 的达到了
计算方法（2016/2017 第一学期）
2
计算方法（2016/2017 第一学期） 西南科技大学 制造科学与工程学院
2
二分法
对于有根区间 a1 , b1 ，在实际操作上，可加中点
a1 b1 x1 a2 , b2 ，可得到新的有根区间 ，长度 2
为原有根区间的一半。
如此反复二分可得一系列有根区间，且
3.4688
3.4531 3.4531
3.4531
3.4453 3.4492
制造科学与工程学院
8
x* x0 。否则 f ( x0 ) 与 f (a) 和 f (b) 的其中一个
异号。 若 f ( x0 )与 f (a) 异号，则取 a1 a, b1 x0 原左半 若 f ( x0 )与 f (b) 异号，则取 a1 x0 , b1 b 原右半 则原方程的有根区间为 a1 , b1 ，它被包含在原区 ba b1 - a1 间 a , b 内，长度为原区间一半，即：

求解方程的近似根，一般需要解决两个问题：1.根的隔离。

即找出有根区域，使得在一些小区间中方程只有一根（或一对共轭复根）以便获取各根的较粗糙的近似值。

2.近似根的精确化。

即用求根的数值方法，使求得的近似根逐步精确化，直到获得一定精度的近似根。

一、二分法和牛顿迭代法的基本思想1.二分法。

一般地，对于函数f （x ），如果存在实数c ，当x=c 时，若f （c ）=0，那么把x=c 叫做函数f （x ）的零点。

解方程即要求f （x ）的所有零点。

假定f （x ）在区间（x ，y ）上连续，先找到a 、b 属于区间（x ，y ），使f （a ），f （b ）异号，说明在区间（a ，b ）内一定有零点，然后求[f （a+b ）/2]，现在假设f （a ）<0，f （b ）>0，a<b ，①如果[f （a+b ）/2]=0，该点就是零点。

如果[f （a+b ）/2]<0，则在区间（（a+b ）/2，b ）内有零点，注：（a+b ）/2>=a ，从①开始继续使用中点函数值判断。

如果[f （a+b ）/2]>0，则在区间（a ，（a+b ）/2）内有零点，注：（a+b ）/2<=b ，从①开始继续使用中点函数值判断。

这样就可以不断接近零点。

通过每次把f （x ）的零点所在小区间收缩一半的方法，使区间的两个端点逐步迫近函数的零点，以求得零点的近似值，这种方法叫做二分法。

从以上可以看出，每次运算后，区间长度减少一半，是线形收敛。

另外，二分法不能计算复根和重根。

2.牛顿迭代法。

设r 是f （x ）=0的根，选取x0作为r 初始近似值，过点（x0，f （x0））做曲线y=f （x ）的切线L ，L 的方程为y=f （x0）+f'（x0）（x-x0），求出L 与x 轴交点的横坐标x1=x0-f（x0）/f'（x0），称x1为r 的一次近似值。

过点（x1，f （x1））作曲线y=f （x ）的切线，并求该切线与x 轴交点的横坐标x2=x1-f（x1）/f'（x1），称x2为r 的二次近似值。

步骤1 输入a , b,精度 1 , 2 ,最大迭代次数 N ,并令 k 0.
步骤2 当k N时, 执行步骤2.1 2.4.
ab 2.1 令x . 2 ba 2.2 若 f ( x ) 1或者 2 , 则输出x , 算法终止. 2
当n 1时,(7.0.2)简化成求解单变量非线性方程
f ( x ) 0
的根.
（ 7.0.3）
在实际问题当中,通常很难精确求解非线性方程(组), 而是利用数值方法近似求解.为此,本章介绍求解非线性方 程(组)的几种常见数值方法： 求解单变量非线性方程 求解多变量非线性方程组
证明 由二分法的步骤可知
bk 1 ak 1 bk 2 ak 2 b1 a1 bk ak k 1 , 2 2 2 2 bk ak * 且 x [ak , bk ], xk . 2 bk ak bk ak b1 a1 ak , 因此， xk x xk ak k 2 2 2
设 为绝对误差容限, 若要求x x (即2 * k
ba

)
两边取对数得k 大于
lg( b a ) / lg 2
lg( b a ) / lg 2
.因此,迭代次数k可取为
的最小整数.
例如,对于例7.1.1,要使得|xk x*| 103 ,只要
xk
0.5 0.25 0.125 0.1875 0.15625 0.171875 0.1796875 0.18359375 0.181640625 0.182617188 0.182128906 0.182373047 0.182250977
f xk
1.375 0.328125 -0.294921875 0.026123047 -0.13192749 -0.052295685 -0.012936115 0.006630838 -0.003143273 0.001746121 -0.000697991 0.000524211 -8.68535e-05

非线性方程求根的常见方法及其应用对于一个非线性方程，其解不一定是唯一的，而且很多情况下解根难以直接求得。

因此，寻找一种可靠、有效的方法来求解非线性方程根是非常重要的。

本文将介绍几种常见的非线性方程求根方法，并且介绍它们的应用场景及求解精度。

一、二分法二分法是一种最基本且易于实现的方法，它能够求解任何单峰函数（函数图像中仅有一个极大值或极小值的函数）的根。

该方法的主要思想是不断缩小根的区间，直到找到根。

具体而言，对于一个单峰函数f(x)，在区间[a,b]上寻找其根。

首先，取中点c=(a+b)/2，计算f(c)。

如果f(c)≈0，则找到了根；否则，根位于[a,c]或[c,b]中的一个区间上，重复上述步骤，直到找到根。

该方法的主要优点是简单易用，适用于大部分单峰函数，并且收敛速度相对较快。

但是，该方法需要区间起点和终点具有异号，否则无法找到根。

二、牛顿迭代法牛顿迭代法是一种高效的方法，可用于求解任何无奇点的连续可微函数的根。

该方法的主要思想是将一个复杂的函数不断逼近于一条直线，然后通过直线和x轴的交点来不断逼近函数的根。

具体而言，对于一个连续可微函数f(x)，在初始点x0处进行求解。

首先，通过f(x)在x=x0处的导数f'(x0)来确定函数的切线。

然后，找到x轴上离该点最近的交点x1处，并将其作为新的起点，迭代上述过程，直到找到根。

该方法的主要优点在于速度快、精度高，并且可适用于大多数函数。

但是，该方法可能会出现迭代过程不稳定的问题，因此需要谨慎选择初值。

三、割线法割线法是一种类似于牛顿迭代法的方法，其主要思想是通过一条割线来逼近函数的根。

相比于牛顿迭代法，割线法更加适用于函数的导数难以求得的情况。

具体而言，对于一个函数f(x)，在初始点x0和x1处进行求解。

首先，通过f(x)在x=x0处和x=x1处的取值来确定割线，找到x轴上与割线交点x2处，并将其作为新的起点，重复上述步骤，直到找到根。

该方法的主要优点在于速度快、精度高，并且可适用于大多数函数。

数学中的非线性方程求解非线性方程是指未知量与其函数之间不满足线性关系的方程。

解决非线性方程的问题一直是数学领域的研究重点之一，因为非线性方程在自然科学、工程技术以及金融经济等领域中具有广泛的应用。

在本文中，我们将探讨几种常见的非线性方程求解方法。

一、二分法二分法也称为区间二分法，是求解非线性方程最基本的方法之一。

该方法利用非线性方程连续性的特点，将方程的解所在的区间不断二分并缩小区间范围，最终找到非线性方程的解。

考虑一个一元非线性方程f(x)=0，其中f(x)在区间[a, b]上连续且f(a)与f(b)异号。

根据区间中值定理可知，存在一点c属于(a, b)，使得f(c)=0。

我们可以按以下步骤进行二分法的求解：步骤1：选择区间[a, b]，计算函数值f(a)与f(b)。

步骤2：如果f(a)与f(b)异号，则继续进行下一步。

否则，结束计算，方程无解。

步骤3：计算区间中点c=(a+b)/2，并计算f(c)。

步骤4：如果f(c)接近于0或满足终止条件，则c为方程解。

否则，根据f(a)与f(c)的符号确定新的区间[a, c]或[c, b]。

步骤5：重复步骤3和步骤4，直至满足终止条件。

二、牛顿法牛顿法是一种迭代逼近的方法，通过使用函数的一阶和二阶导数来逼近非线性方程的解。

该方法基于泰勒级数展开，通过不断迭代逼近函数零点的位置。

考虑一个一元非线性方程f(x)=0，我们可以按以下步骤进行牛顿法的求解：步骤1：选择一个初始近似值x0。

步骤2：计算函数f(x)的一阶导数f'(x)和二阶导数f''(x)。

步骤3：使用初始近似值x0和函数导数来进行迭代计算，得到新的近似值x1。

迭代公式为x1 = x0 - f(x0)/f'(x0)。

步骤4：计算函数f(x1)的值。

步骤5：如果f(x1)接近于0或满足终止条件，则x1为方程解。

否则，将x1作为新的近似值，重复步骤3和步骤4。

步骤6：重复步骤3至步骤5，直至满足终止条件。

在给出了用二分法求解一元超越方程 和二元方程组的思路之后，我们把求解多 元的方程组转化到求解一元方程来达到求 解的目的。对于一个有三元的方程组来 说，可先给定其中一个元的初值，使方程组 变成一个二元的方程组和一个二元方程，
然后用 ３ 部分所述方法解出二元方程组， 再把方程组的解集代入剩下的一个方程 中，求出其函数值；再增加给定元一个步 长值，使方程组变成一个二元的方程组和 一个二元方程，然后用 ３ 部分所述方法解 出二元方程组，再把方程组的解集代入剩 下的一个方程中，求出这时的函数值，并与 前一次的函数值相乘，若乘积小于零，则在 这个步长中方程组有解，可用二部分所述 方法求出解集；若大于零，则此步长区间 中无解，则增加给定元一个步长值，重复前 面的步骤，直到给定元取值结束。对于 Ｎ 元方程组则是以此类推。解 Ｎ 元方程组的 流程图如下：如图 ３。
学 术 论 坛
（３）和（４）变为：
ｆ１ （ｘ１，ａ２＋ｈ）＝０ ， （５） ｙ２＝ ｆ２（ｘ１，ａ２＋ｈ）， （６） 再用 ２ 中介绍的的方法解一元方程
（５），解出 ｘ１，把解出的 ｘ１ 值代入 ｙ２，求出其 函数值，并与前一次的函数值相乘，若乘积
小于零，则在 ｘ２ 的这一个步长中，方程组有 解，可用二部分所述二分这个步长的方法
“御使轿夫、家奴庆和园兹事，梨园公 愤罢演七天”
光绪十五年七月二十一、二十二日， 左御使许应騤和副都御使杨颐家中轿夫、 家奴张大顺、张文纪等数人，在大栅栏庆 和园戏园肆意兹事，还仗势伙同巡城御使、 中城坊官正指挥等人私自封闭庆和园，斥 责戏园卯头，当即引起周边各处戏园、戏 班同僚的一致不满。经孙菊仙、杨月楼等 诸庙首、戏园园主、戏班班主及各界票友、 友人共议，决定不能纵容此事。遂京城梨园
７ 版．北京：高等教育出版社，２００１． ［５］ 罗坚等．Ｃ 语言程序设计［Ｍ］．北京：中国

非线性方程的数值解法中的二分法作者：何天荣来源：《科技风》2016年第13期摘要：代数方程的求根问题是一个古老的数学问题，早在16世纪就找到了三次、四次方程的求根公式。

但直到19世纪才证明高于5次的一般代数方程式不能用代数公式求解。

因此，需要研究用数值方法求得满足一定精度的代数方程式近似解。

本文就二分法的理论、方法、例题方面进行阐述。

关键词：非线性方程；数值解法；二分法1 二分法的理论依据定理1[ 1 ] （1）设f（x）于[a，b]上连续；（2）且f（a）·f（b）定理1的理论依据来源于数学分析闭区间上连续函数的介值性定理。

叙述如下：定理2（介值性定理）[ 2 ] 设函数f（x）于[a，b]上连续，且f（a）≠f（b）。

若？滋为介于f（a）和f（b）之间的任何常数（f（a）？滋>f（b）），则至少存在一点x0∈（a，b），使得f（x0）=？滋。

定理的证明参见[2]，而定理1称为根的存在性定理，它是介质定理的特殊情况，即假设f（a）>0，f（b）0情况下的介质定理中f（x）=0的结论。

2 二分法的过程叙述设有非线性方程f（x）=0，其中，设f（x）为[a，b]上的连续函数且设f（a）·f（b）第1步分半计算（k=1）：于是得到长度缩小一半的含根区间第k步分半计算：重复上述过程，设已完成第1步、…、现进行第k步分半计算：总之，由上述二分法得到一序列；可用二分法求方程f（x）=0实根到任意指定的精度。

事实上例插用二分法求方程x3-2x2-4x-7=0在区间[3，4]内的根，精确到10-3，即误差不超过解：因为f（3）=-100，所以，方程在区间[3，4]上有根。

所以n=11，即只需要二分11次即可。

列表讨论如下：参考文献：[1] 易大义，沈云宝，李有法编.计算方法（第二版）[M].浙江大学出版社，2012.[2] 华东师大数学系编.数学分析（第三版）[M].北京：高等教育出版社，2010.。

} void main() { double x1,x2,a,b,e2=1; int i = 0,e1; printf("请输入根的区间："); scanf("%lf",&a); scanf("%lf",&b); if((f(a)*f(b))<0) { printf("要求小数点后的位数："); scanf("%d",&e1); while(e1>0) { e2=e2/10; e1--; } e2=e2/2; printf("e2=%f",e2); x1=a; printf("第%d 次迭代后结果是：%20.19f\n",i,x1); x2=f(x1); while(fabs(x2-x1)>e2) { i++; printf("第%d 次迭代后结果是：%20.19f\n",i,x2); x1=x2; x2=fdao(x1); } printf("共进行%d 次迭代过程\n",i); printf("结果是：%20.19f\n",x2); } else printf("无法进行迭代!"); }
及 实 验 步 骤
（3）撰写实验报告 2、实验 2 实验步骤： （1）程序设计 （2）计算实例 （3）撰写实验报告 1、 二分法求根实验结果如图：
调 试 过 程 及 实 验 结 果
2、 迭代法的求根实验结果如图：
总 结
附 录
1、 通过本次实验，使我掌握了使用二分法求非线性方程的根，加深了对 二分法的了解。 2、 通过本次实验，使我掌握了使用迭代法求非线性方程的根的方法，能 够使用使用迭代法正确的求出求非线性方程的根。 1、 二分法程序清单： #include<stdio.h> #include<math.h> #include<conio.h> double f(double x) { double y = 0; y = sin(x) - x*x/2; return y; } void main() { double a,b,y1,y2,temp; int e1,e2=1,n,i=0; printf("请输入根的区间："); scanf("%lf",&a); scanf("%lf",&b); y1=f(a); y2=f(b); if((y1*y2)<0)