第一章金属的晶体结构1
- 格式:ppt
- 大小:3.87 MB
- 文档页数:32

第一章金属的晶体结构本章重点与难点:①金属键;②最常见的晶体结构:面心立方结构(fcc)、体心立方结构(bcc)、密排六方结构(hcp);晶向指数和晶面指数;③晶体中存在的缺陷:点缺陷、面缺陷、线缺陷。
内容提要:固体物质的原子是由键结合在一起。
这些键提供了固体的强度和有关电和热的性质。
由于原子间的结合键不同,我们经常将材料分为金属、聚合物和陶瓷三类。
金属的原子之间时依靠金属键结合在一起的。
在结晶固体中,材料的许多性能都与其内部原子排列有关,可将晶体分为7种晶系,14种布拉菲点阵。
金属中最常见的晶体结构有面心立方结构(fcc)、体心立方结构(bcc)、密排六方结构(hcp)结构。
本章还介绍了晶向、晶面的概念及其表示方法(指数),因为这些指数被用来建立晶体结构和材料性质及行为间的关系。
实际的晶体结构中存在着一些缺陷,根据几何形态特征,分为点缺陷、面缺陷、线缺陷。
基本要求:1.建立原子结构的特征,了解影响原子大小的各种因素。
3.建立单位晶胞的概念,以便用来想像原子的排列;在不同晶向和镜面上所存在的长程规则性;在一维、二维和三维空间的堆积密度。
4.熟悉常见晶体中原子的规则排列形式,特别是bcc,fcc以及hcp。
我们看到的面心立方结构,除fcc金属结构外,还有NaCl结构和金刚石立方体结构。
5. 掌握晶向、晶面指数的标定方法。
一般由原点至离原点最近一个结点(u,v,w)的连线来定其指数。
如此放像机定为[u,v,w]。
u,v,w之值必须使互质。
晶面指数微晶面和三轴相交的3个截距系数的倒数,约掉分数和公因数之后所得到的最小整数值。
若给出具体的晶向、镜面时会标注“指数”时,会在三维空间图上画出其位置。
6.认识晶体缺陷的基本类型、基本特征、基本性质。
注意位错线与柏氏矢量,位错线移动方向、晶体滑移方向与外加切应力方向之间的关系。
7 了解位错的应力场和应变能,位错的增殖、塞积与交割。
第一节金属1 金属原子的结构特点金属原子的结构特点是外层电子少,容易失去。


第⼀章⾦属的晶体结构作业答案第⼀章⾦属的晶体结构1、试⽤⾦属键的结合⽅式,解释⾦属具有良好的导电性、正的电阻温度系数、导热性、塑性和⾦属光泽等基本特性.答:(1)导电性:在外电场的作⽤下,⾃由电⼦沿电场⽅向作定向运动。
(2)正的电阻温度系数:随着温度升⾼,正离⼦振动的振幅要加⼤,对⾃由电⼦通过的阻碍作⽤也加⼤,即⾦属的电阻是随温度的升⾼⽽增加的。
(3)导热性:⾃由电⼦的运动和正离⼦的振动可以传递热能。
(4) 延展性:⾦属键没有饱和性和⽅向性,经变形不断裂。
(5)⾦属光泽:⾃由电⼦易吸收可见光能量,被激发到较⾼能量级,当跳回到原位时辐射所吸收能量,从⽽使⾦属不透明具有⾦属光泽。
2、填空:1)⾦属常见的晶格类型是⾯⼼⽴⽅、体⼼⽴⽅、密排六⽅。
2)⾦属具有良好的导电性、导热性、塑性和⾦属光泽主要是因为⾦属原⼦具有⾦属键的结合⽅式。
3)物质的原⼦间结合键主要包括⾦属键、离⼦键和共价键三种。
4)⼤部分陶瓷材料的结合键为共价键。
5)⾼分⼦材料的结合键是范德⽡尔键。
6)在⽴⽅晶系中,某晶⾯在x轴上的截距为2,在y轴上的截距为1/2;与z轴平⾏,则该晶⾯指数为(( 140 )).7)在⽴⽅晶格中,各点坐标为:A (1,0,1),B (0,1,1),C (1,1,1/2),D(1/2,1,1/2),那么AB晶向指数为(ī10),OC晶向指数为(221),OD晶向指数为(121)。
8)铜是(⾯⼼)结构的⾦属,它的最密排⾯是(111 )。
9) α-Fe、γ-Fe、Al、Cu、Ni、Cr、V、Mg、Zn中属于体⼼⽴⽅晶格的有(α-Fe 、 Cr、V ),属于⾯⼼⽴⽅晶格的有(γ-Fe、Al、Cu、Ni ),属于密排六⽅晶格的有( Mg、Zn )。
3、判断1)正的电阻温度系数就是指电阻随温度的升⾼⽽增⼤。
(√)2)⾦属具有美丽的⾦属光泽,⽽⾮⾦属则⽆此光泽,这是⾦属与⾮⾦属的根本区别。
(×)3) 晶体中原⼦偏离平衡位置,就会使晶体的能量升⾼,因此能增加晶体的强度。

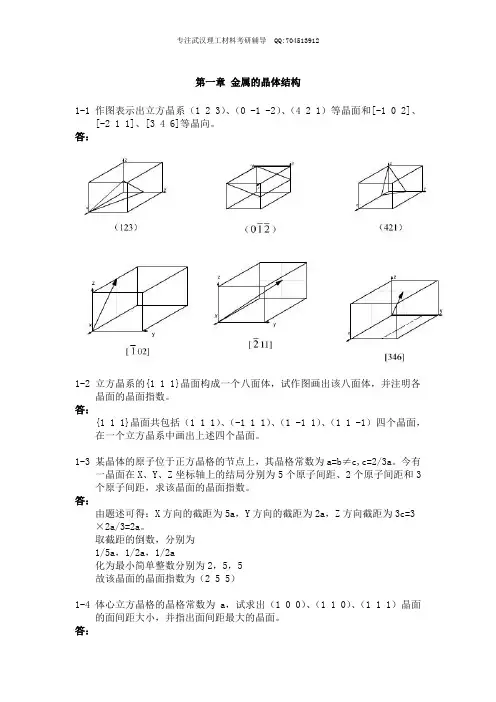
第一章金属的晶体结构1-1 作图表示出立方晶系(1 2 3)、(0 -1 -2)、(4 2 1)等晶面和[-1 0 2]、[-2 1 1]、[3 4 6]等晶向。
答:1-2 立方晶系的{1 1 1}晶面构成一个八面体,试作图画出该八面体,并注明各晶面的晶面指数。
答:{1 1 1}晶面共包括(1 1 1)、(-1 1 1)、(1 -1 1)、(1 1 -1)四个晶面,在一个立方晶系中画出上述四个晶面。
1-3 某晶体的原子位于正方晶格的节点上,其晶格常数为a=b≠c,c=2/3a。
今有一晶面在X、Y、Z坐标轴上的结局分别为5个原子间距、2个原子间距和3个原子间距,求该晶面的晶面指数。
答:由题述可得:X方向的截距为5a,Y方向的截距为2a,Z方向截距为3c=3×2a/3=2a。
取截距的倒数,分别为1/5a,1/2a,1/2a化为最小简单整数分别为2,5,5故该晶面的晶面指数为(2 5 5)1-4 体心立方晶格的晶格常数为a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的面间距大小,并指出面间距最大的晶面。
答:H==a/2(1 0 0)==√2a/2H(1 1 0)==√3a/6H(1 1 1)面间距最大的晶面为(1 1 0)1-5 面心立方晶格的晶格常数为a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的面间距大小,并指出面间距最大的晶面。
答:==a/2H(1 0 0)H==√2a/4(1 1 0)==√3a/3H(1 1 1)面间距最大的晶面为(1 1 1)注意:体心立方晶格和面心立方晶格晶面间距的计算方法是:1、体心立方晶格晶面间距:当指数和为奇数是H=,当指数和为偶数时H=2、面心立方晶格晶面间距:当指数不全为奇数是H=,当指数全为奇数是H=。
1-6 试从面心立方晶格中绘出体心正方晶胞,并求出它的晶格常数。
答:1-7 证明理想密排六方晶胞中的轴比c/a=1.633。


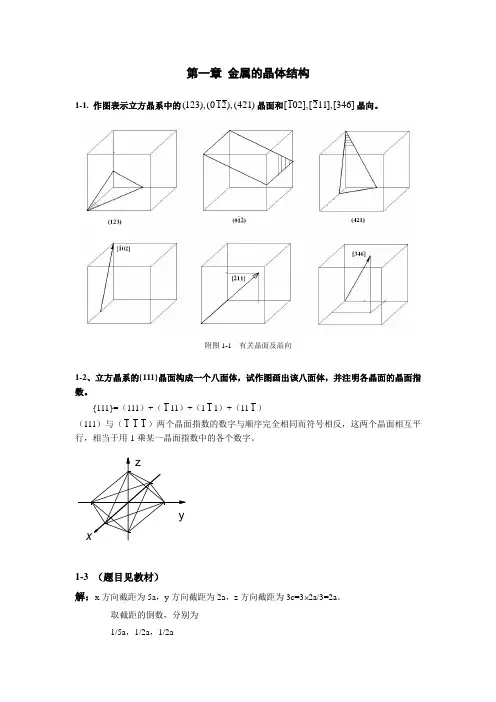
第一章金属的晶体结构1-1. 作图表示立方晶系中的(123),(012),(421)晶面和[102],[211],[346]晶向。
附图1-1 有关晶面及晶向1-2、立方晶系的{111}晶面构成一个八面体,试作图画出该八面体,并注明各晶面的晶面指数。
{111}=(111)+(111)+(111)+(111)(111)与(111)两个晶面指数的数字与顺序完全相同而符号相反,这两个晶面相互平行,相当于用-1乘某一晶面指数中的各个数字。
xy z1-3 (题目见教材)解:x方向截距为5a,y方向截距为2a,z方向截距为3c=3 2a/3=2a。
取截距的倒数,分别为1/5a,1/2a,1/2a化为最小简单整数分别为2,5,5 故该晶面的晶面指数为(2 5 5)1-4 (题目见课件)解:(100)面间距为a/2;(110)面间距为2a/2;(111)面间距为3a/3。
三个晶面中面间距最大的晶面为(110)。
1-5 (题目见课件)解:方法同1-4题1-7 证明理想密排六方晶胞中的轴比c/a=1.633。
证明:理想密排六方晶格配位数为12,即晶胞上底面中心原子与其下面的3个位于晶胞内的原子相切,构成正四面体,如图所示。
则OD=2c,AB=BC=CA=AD=BD=CD=a 因∆ABC 是等边三角形,所以有OC=32CE 因(BC)2=(CE)2+(BE)2则CE=23a ,OC=32×23a =33a又(CD)2=(OC)2+(21c )2,即(CD)2=(33a )2+(21c )2=(a )2因此,ac=38≈1.6331-8解:面心立方八面体间隙半径 r=a/2-2a/4=0.146a , 面心立方原子半径R=2a/4,则a=4R/2,代入上试有CBADEOr=0.146⨯4R/2=0.414R。
(其他的证明类似)1-9 a)设有一刚球模型,球的直径不变,当由面心立方晶格转变为体心立方晶格时,试计算其体积的膨胀?b)经X射线测定,在912℃时γ-Fe的晶格常数为0.3633nm,α-Fe的晶格常数为0.2892nm,当由γ-Fe转变为α-Fe时,试求其体积膨胀? c)分析实际体积膨胀小于理论体积膨胀的原因?解:a)令面心立方晶格与体心立方晶格的体积及晶格常数分别为V面、V体与a面、a体,刚球半径为r,由晶体结构可知,对于面心晶胞有4r=2a面,a面=22r,V面= (a面)3=(22r)3对于体心晶胞有4r=3a体,a体=334r,V体= (a体)3=(334r)3则由面心立方晶胞转变为体心立方晶胞的体积膨胀∆V为∆V=2×V体-V面=2.01r3b)按晶格常数计算实际转变体积膨胀∆V实,有∆V实=2×V体-V面=2×(0.2892)3-(0.3633)3=0.000425 nm3c)实际体积膨胀小于理论体积膨胀的原因在于由γ-Fe转变为α-Fe时,Fe 原子半径发生了变化,原子半径减小了。



《工程材料》复习思考题参考答案第一章金属的晶体结构与结晶1.解释下列名词点缺陷,线缺陷,面缺陷,亚晶粒,亚晶界,刃型位错,单晶体,多晶体,过冷度,自发形核,非自发形核,变质处理,变质剂.答:点缺陷:原子排列不规则的区域在空间三个方向尺寸都很小,主要指空位间隙原子、置换原子等。
线缺陷:原子排列的不规则区域在空间一个方向上的尺寸很大,而在其余两个方向上的尺寸很小.如位错。
面缺陷:原子排列不规则的区域在空间两个方向上的尺寸很大,而另一方向上的尺寸很小.如晶界和亚晶界.亚晶粒:在多晶体的每一个晶粒内,晶格位向也并非完全一致,而是存在着许多尺寸很小、位向差很小的小晶块,它们相互镶嵌而成晶粒,称亚晶粒。
亚晶界:两相邻亚晶粒间的边界称为亚晶界。
刃型位错:位错可认为是晶格中一部分晶体相对于另一部分晶体的局部滑移而造成。
滑移部分与未滑移部分的交界线即为位错线。
如果相对滑移的结果上半部分多出一半原子面,多余半原子面的边缘好像插入晶体中的一把刀的刃口,故称“刃型位错”。
单晶体:如果一块晶体,其内部的晶格位向完全一致,则称这块晶体为单晶体。
多晶体:由多种晶粒组成的晶体结构称为“多晶体”。
过冷度:实际结晶温度与理论结晶温度之差称为过冷度。
自发形核:在一定条件下,从液态金属中直接产生,原子呈规则排列的结晶核心.非自发形核:是液态金属依附在一些未溶颗粒表面所形成的晶核。
变质处理:在液态金属结晶前,特意加入某些难熔固态颗粒,造成大量可以成为非自发晶核的固态质点,使结晶时的晶核数目大大增加,从而提高了形核率,细化晶粒,这种处理方法即为变质处理。
变质剂:在浇注前所加入的难熔杂质称为变质剂.2.常见的金属晶体结构有哪几种?α—Fe 、γ- Fe 、Al 、Cu 、Ni 、Pb 、Cr 、V 、Mg、Zn 各属何种晶体结构?答:常见金属晶体结构:体心立方晶格、面心立方晶格、密排六方晶格;α-Fe、Cr、V属于体心立方晶格;γ-Fe 、Al、Cu、Ni、Pb属于面心立方晶格;Mg、Zn属于密排六方晶格;3.配位数和致密度可以用来说明哪些问题?答:用来说明晶体中原子排列的紧密程度。
第一章金属的晶体结构习题答案第一章金属的晶体结构习题答案第一章金属的晶体结构(一)填空题3.金属晶体中常见的点缺陷是空位、间隙原子和置换原子,最主要的面缺陷是。
4.位错密度是指单位体积中所包含的位错线的总长度,其数学表达式为??l。
v5.表示晶体中原子排列形式的空间格子叫做晶格,而晶胞是指从晶格中选取一个能够完全反应晶格特征的最小几何单元。
6.在普通金属晶格中,体心立方晶格中原子排列最密集的晶体方向为[111],面心立方晶格为[110]。
7晶体在不同晶向上的性能是不同的,这就是单晶体的各向异性现象。
一般结构用金属为多晶体,在各个方向上性能相同,这就是实际金属的伪等向性现象。
8实际金属存在有点缺陷、线缺陷和面缺陷三种缺陷。
位错是线缺陷。
9.在室温下使用的金属材料首选细晶粒。
在一定范围内,高温下使用的金属材料具有较粗的晶粒。
10.金属常见的晶格类型是面心立方、体心立方、密排六方。
11.在立方晶格中,每个点的坐标是:a(1,0,1),B(0,1,1),C(1,1,1/2),D (1/2,1,1/2),那么AB晶体方向指数是[110],OC晶体方向指数是[221],OD晶体方向指数是[121]。
12.铜是一种具有面心结构的金属,其最近平面为{111}。
如果铜的晶格常数为a=0.36nm,那么最密排面上原子间距为0.509nm。
十三个α-fe、γ-在铁、铝、铜、镍、铬、钒、镁和锌中,有α-fe、铬、镁和锌v,属于面心立方晶格的有γ-fe、al、cu、ni、,属于密排六方晶格的有mg、zn。
14.假设铜的原子直径为0.256nm,铜的晶格常数为。
1mm3cu中的原子数为。
15.晶面通过三个点(0,0,0),(1/2,1/4,0)和(1/2,0,1/2)。
该晶面的晶面指数为。
16.在立方晶体系统中,晶体平面在X轴上的截距为2,在Y轴上的截距为1/2;平行于z轴,然后该晶面指数为(140).17.金属具有良好的导电性、导热性、塑性和金属光泽主要是因为金属原子具有金属键的组合模式。