第一章金属晶体结构

第一章金属的晶体结构本章重点与难点：①金属键；②最常见的晶体结构：面心立方结构（fcc）、体心立方结构（bcc）、密排六方结构（hcp）；晶向指数和晶面指数；③晶体中存在的缺陷：点缺陷、面缺陷、线缺陷。

内容提要：固体物质的原子是由键结合在一起。

这些键提供了固体的强度和有关电和热的性质。

由于原子间的结合键不同，我们经常将材料分为金属、聚合物和陶瓷三类。

金属的原子之间时依靠金属键结合在一起的。

在结晶固体中，材料的许多性能都与其内部原子排列有关，可将晶体分为7种晶系，14种布拉菲点阵。

金属中最常见的晶体结构有面心立方结构（fcc）、体心立方结构（bcc）、密排六方结构（hcp）结构。

本章还介绍了晶向、晶面的概念及其表示方法（指数），因为这些指数被用来建立晶体结构和材料性质及行为间的关系。

实际的晶体结构中存在着一些缺陷，根据几何形态特征，分为点缺陷、面缺陷、线缺陷。

基本要求：1.建立原子结构的特征，了解影响原子大小的各种因素。

3.建立单位晶胞的概念，以便用来想像原子的排列；在不同晶向和镜面上所存在的长程规则性;在一维、二维和三维空间的堆积密度。

4.熟悉常见晶体中原子的规则排列形式，特别是bcc，fcc以及hcp。

我们看到的面心立方结构，除fcc金属结构外，还有NaCl结构和金刚石立方体结构。

5. 掌握晶向、晶面指数的标定方法。

一般由原点至离原点最近一个结点（u,v,w）的连线来定其指数。

如此放像机定为[u,v,w]。

u,v,w之值必须使互质。

晶面指数微晶面和三轴相交的3个截距系数的倒数，约掉分数和公因数之后所得到的最小整数值。

若给出具体的晶向、镜面时会标注“指数”时，会在三维空间图上画出其位置。

6.认识晶体缺陷的基本类型、基本特征、基本性质。

注意位错线与柏氏矢量，位错线移动方向、晶体滑移方向与外加切应力方向之间的关系。

7 了解位错的应力场和应变能，位错的增殖、塞积与交割。

第一节金属1 金属原子的结构特点金属原子的结构特点是外层电子少，容易失去。

第⼀章⾦属的晶体结构作业答案第⼀章⾦属的晶体结构1、试⽤⾦属键的结合⽅式，解释⾦属具有良好的导电性、正的电阻温度系数、导热性、塑性和⾦属光泽等基本特性.答：(1)导电性：在外电场的作⽤下，⾃由电⼦沿电场⽅向作定向运动。

(2)正的电阻温度系数：随着温度升⾼，正离⼦振动的振幅要加⼤，对⾃由电⼦通过的阻碍作⽤也加⼤，即⾦属的电阻是随温度的升⾼⽽增加的。

(3)导热性：⾃由电⼦的运动和正离⼦的振动可以传递热能。

(4) 延展性：⾦属键没有饱和性和⽅向性，经变形不断裂。

(5)⾦属光泽：⾃由电⼦易吸收可见光能量，被激发到较⾼能量级，当跳回到原位时辐射所吸收能量，从⽽使⾦属不透明具有⾦属光泽。

2、填空：1)⾦属常见的晶格类型是⾯⼼⽴⽅、体⼼⽴⽅、密排六⽅。

2)⾦属具有良好的导电性、导热性、塑性和⾦属光泽主要是因为⾦属原⼦具有⾦属键的结合⽅式。

3)物质的原⼦间结合键主要包括⾦属键、离⼦键和共价键三种。

4)⼤部分陶瓷材料的结合键为共价键。

5)⾼分⼦材料的结合键是范德⽡尔键。

6)在⽴⽅晶系中，某晶⾯在x轴上的截距为2，在y轴上的截距为1/2；与z轴平⾏，则该晶⾯指数为（（ 140 ））.7)在⽴⽅晶格中，各点坐标为：A (1，0，1)，B (0，1，1)，C (1，1，1/2)，D(1/2，1，1/2)，那么AB晶向指数为（ī10），OC晶向指数为（221），OD晶向指数为（121）。

8)铜是（⾯⼼）结构的⾦属，它的最密排⾯是（111 ）。

9) α-Fe、γ-Fe、Al、Cu、Ni、Cr、V、Mg、Zn中属于体⼼⽴⽅晶格的有（α-Fe 、 Cr、V ），属于⾯⼼⽴⽅晶格的有（γ-Fe、Al、Cu、Ni ），属于密排六⽅晶格的有（ Mg、Zn ）。

3、判断1)正的电阻温度系数就是指电阻随温度的升⾼⽽增⼤。

（√）2)⾦属具有美丽的⾦属光泽，⽽⾮⾦属则⽆此光泽，这是⾦属与⾮⾦属的根本区别。

（×）3) 晶体中原⼦偏离平衡位置，就会使晶体的能量升⾼，因此能增加晶体的强度。

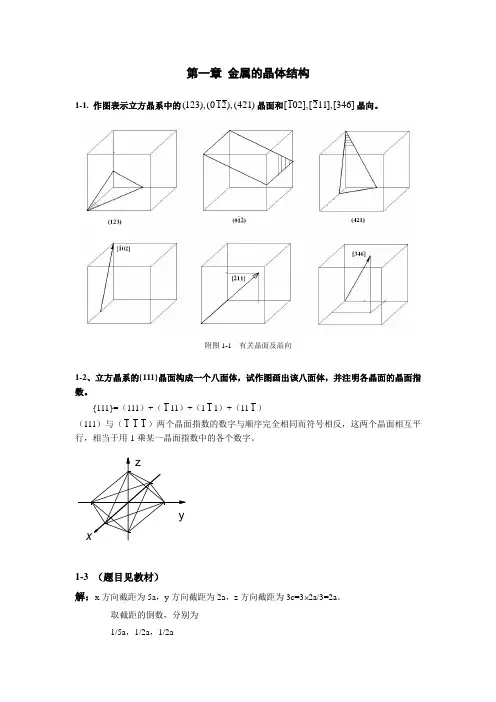
第一章金属的晶体结构1-1. 作图表示立方晶系中的(123),(012),(421)晶面和[102],[211],[346]晶向。

附图1-1 有关晶面及晶向1-2、立方晶系的{111}晶面构成一个八面体，试作图画出该八面体，并注明各晶面的晶面指数。

{111}=（111）+（111）+（111）+（111）（111）与（111）两个晶面指数的数字与顺序完全相同而符号相反，这两个晶面相互平行，相当于用-1乘某一晶面指数中的各个数字。

xy z1-3 （题目见教材）解：x方向截距为5a，y方向截距为2a，z方向截距为3c=3 2a/3=2a。

取截距的倒数，分别为1/5a，1/2a，1/2a化为最小简单整数分别为2，5，5 故该晶面的晶面指数为（2 5 5）1-4 （题目见课件）解：（100）面间距为a/2；（110）面间距为2a/2；（111）面间距为3a/3。

三个晶面中面间距最大的晶面为（110）。

1-5 （题目见课件）解：方法同1-4题1-7 证明理想密排六方晶胞中的轴比c/a=1.633。

证明：理想密排六方晶格配位数为12，即晶胞上底面中心原子与其下面的3个位于晶胞内的原子相切，构成正四面体，如图所示。

则OD=2c，AB=BC=CA=AD=BD=CD=a 因∆ABC 是等边三角形，所以有OC=32CE 因(BC)2=(CE)2+(BE)2则CE=23a ，OC=32×23a =33a又(CD)2=(OC)2+(21c )2，即(CD)2=(33a )2+(21c )2=(a )2因此，ac=38≈1.6331-8解：面心立方八面体间隙半径 r=a/2-2a/4=0.146a ， 面心立方原子半径R=2a/4，则a=4R/2，代入上试有CBADEOr=0.146⨯4R/2=0.414R。

（其他的证明类似）1-9 a）设有一刚球模型，球的直径不变，当由面心立方晶格转变为体心立方晶格时，试计算其体积的膨胀？b）经X射线测定，在912℃时γ-Fe的晶格常数为0.3633nm，α-Fe的晶格常数为0.2892nm，当由γ-Fe转变为α-Fe时，试求其体积膨胀? c）分析实际体积膨胀小于理论体积膨胀的原因？解：a）令面心立方晶格与体心立方晶格的体积及晶格常数分别为V面、V体与a面、a体，刚球半径为r，由晶体结构可知，对于面心晶胞有4r=2a面，a面=22r，V面= (a面)3=(22r)3对于体心晶胞有4r=3a体，a体=334r，V体= (a体)3=(334r)3则由面心立方晶胞转变为体心立方晶胞的体积膨胀∆V为∆V=2×V体－V面=2.01r3b）按晶格常数计算实际转变体积膨胀∆V实，有∆V实=2×V体－V面=2×(0.2892)3－(0.3633)3=0.000425 nm3c）实际体积膨胀小于理论体积膨胀的原因在于由γ-Fe转变为α-Fe时，Fe 原子半径发生了变化，原子半径减小了。