金属的晶体结构(第1讲)
- 格式:ppt
- 大小:1.82 MB
- 文档页数:37




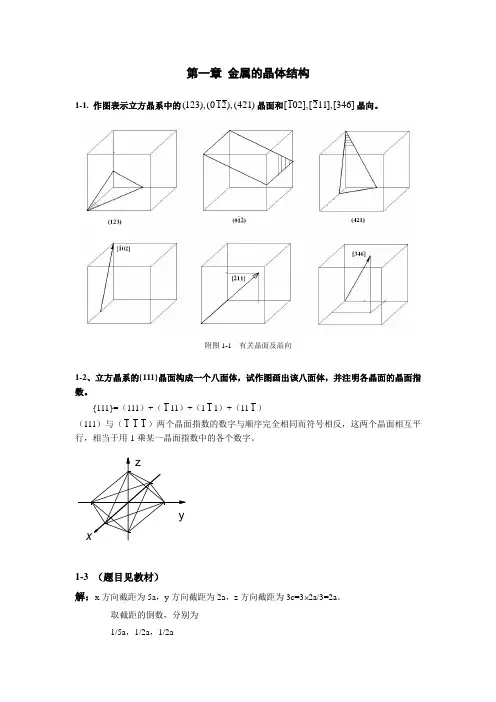
第一章金属的晶体结构1-1. 作图表示立方晶系中的(123),(012),(421)晶面和[102],[211],[346]晶向。
附图1-1 有关晶面及晶向1-2、立方晶系的{111}晶面构成一个八面体,试作图画出该八面体,并注明各晶面的晶面指数。
{111}=(111)+(111)+(111)+(111)(111)与(111)两个晶面指数的数字与顺序完全相同而符号相反,这两个晶面相互平行,相当于用-1乘某一晶面指数中的各个数字。
xy z1-3 (题目见教材)解:x方向截距为5a,y方向截距为2a,z方向截距为3c=3 2a/3=2a。
取截距的倒数,分别为1/5a,1/2a,1/2a化为最小简单整数分别为2,5,5 故该晶面的晶面指数为(2 5 5)1-4 (题目见课件)解:(100)面间距为a/2;(110)面间距为2a/2;(111)面间距为3a/3。
三个晶面中面间距最大的晶面为(110)。
1-5 (题目见课件)解:方法同1-4题1-7 证明理想密排六方晶胞中的轴比c/a=1.633。
证明:理想密排六方晶格配位数为12,即晶胞上底面中心原子与其下面的3个位于晶胞内的原子相切,构成正四面体,如图所示。
则OD=2c,AB=BC=CA=AD=BD=CD=a 因∆ABC 是等边三角形,所以有OC=32CE 因(BC)2=(CE)2+(BE)2则CE=23a ,OC=32×23a =33a又(CD)2=(OC)2+(21c )2,即(CD)2=(33a )2+(21c )2=(a )2因此,ac=38≈1.6331-8解:面心立方八面体间隙半径 r=a/2-2a/4=0.146a , 面心立方原子半径R=2a/4,则a=4R/2,代入上试有CBADEOr=0.146⨯4R/2=0.414R。
(其他的证明类似)1-9 a)设有一刚球模型,球的直径不变,当由面心立方晶格转变为体心立方晶格时,试计算其体积的膨胀?b)经X射线测定,在912℃时γ-Fe的晶格常数为0.3633nm,α-Fe的晶格常数为0.2892nm,当由γ-Fe转变为α-Fe时,试求其体积膨胀? c)分析实际体积膨胀小于理论体积膨胀的原因?解:a)令面心立方晶格与体心立方晶格的体积及晶格常数分别为V面、V体与a面、a体,刚球半径为r,由晶体结构可知,对于面心晶胞有4r=2a面,a面=22r,V面= (a面)3=(22r)3对于体心晶胞有4r=3a体,a体=334r,V体= (a体)3=(334r)3则由面心立方晶胞转变为体心立方晶胞的体积膨胀∆V为∆V=2×V体-V面=2.01r3b)按晶格常数计算实际转变体积膨胀∆V实,有∆V实=2×V体-V面=2×(0.2892)3-(0.3633)3=0.000425 nm3c)实际体积膨胀小于理论体积膨胀的原因在于由γ-Fe转变为α-Fe时,Fe 原子半径发生了变化,原子半径减小了。



引言金属学是研究金属及合金的成分、组织、结构与力学性能之间关系的科学。
所谓力学性能主要指材料的强度、硬度和塑性。
通常用来承受载荷的零件要求材料具有一定的力学性能,我们称这类材料为结构材料。
与结构材料对应的另一类材料是功能材料,它一般不要求承受载荷,主要使用它的物理性能,如光、电、磁性能等。
功能材料利用它对光、电、磁的敏感特性制作各类传感器。
金属学只讨论金属材料的力学性能,不涉及物理性能。
固态金属通常是晶体,金属学研究的最小结构单元是原子。
原子通过不同的排列可构成各种不同的晶体结构,产生不同的性能。
原子结构不是金属学研究的范畴。
第1章金属的晶体结构1-1金属及金属键金属的定义根据学科的不同有多种划分方法。
本人倾向按结合键的性质来划分,即金属是具有金属键的一类物质。
这种分类的好处是有利于解释与金属力学性能相关的现象。
例如,为什么金属具有较好的塑性?什么是金属键、离子键、共价键我们早就熟知,金属键的最大特点是无饱和性、无方向性。
以后我们将会看到,正是这些特点使金属具有较好的塑性。
研究表明,固态金属通常是晶体,且其结构趋于密堆积结构。
这是为什么?下面我们用双原子模型来说明。
当两个原子相距很远时,它们之间不发生作用。
当它们逐渐靠近时,一个原子的原子核与另一个原子的核外电子之间将产生引力;而两原子的原子核及电子之间产生斥力。
研究表明,引力是长程力,斥力是短程力,即距离较远时,引力大于斥力,表现为相互吸引。
随着原子距离的减小,斥力增加的速度逐渐大于引力增加的速度。
显然这样作用的结果必然存在一个平衡距离d0,此时,引力等于斥力,偏离这一距离时,都将受到一个恢复力,如P3图2。
d c对应最大恢复引力,即最大结合力,它对应着金属的理论抗拉强度。
下面,我们从能量的角度来考虑系统的稳定性。
在引力作用下原子移近所做的功使原子的势能降低,所以吸引能是负值。
相反,排斥能是正值。
吸引能和排斥能的代数和是结合能。
由P3图2可以看出,当原子移至平衡距离d0时,其结合能达到最低值,此时系统的势能最低,状态最稳定。

